雙聯拱隧道結構模型數值分析與優化設計

馬帥帥　孫厚超　許龔成　陳榮剛　殷勇

摘? 要：結合第四屆全國城市地下空間工程專業大學生模型設計競賽，建立了雙聯拱隧道數值模型，分析了各計算工況。根據有限元數值模型計算結果，對各工況下模型頂部豎向位移、構件最大側向位移及構件最大軸力對比分析，提出了隧道支護結構模型優化設計建議。

關鍵詞：隧道結構模型;數值分析;方案設計;構件優化

中圖分類號：U455.4? ? ? ? ?文獻標志碼：A? ? ? ? ?文章編號：2095-2945（2020）07-0004-05

Abstract： Based on the fourth national model design competition for college students majoring in urban underground space engineering， the numerical model of double-arch tunnel is established， and the calculation conditions are analyzed. According to the calculation results of the finite element numerical model， this paper makes a comparative analysis of the vertical displacement at the top of the model， the maximum lateral displacement and the maximum axial force of the members under various working conditions， and puts forward some suggestions for the optimal design of the tunnel supporting structure model.

Keywords： tunnel structure model; numerical analysis; scheme design; component optimization

1 概述

隨著交通建設的不斷發展，經常遇到隧道工程問題，隧道設計是地下建筑結構的重要組成部分，它包括半襯砌結構、厚拱薄墻襯砌結構、直墻拱形襯砌結構、曲墻結構、復合襯砌結構和連拱隧道結構等形式，實際工程中可根據地層類別、使用功能和施工技術水平等因素進行選擇。在諸多隧道結構形式中，雙連拱隧道滿足上、下行車分離的要求，接線難度小、占地少、有利于環境保護等特點，而且在平面線路、洞口位置選擇自由度大，因此，在短隧道設計中得到普遍采用。目前，隧道結構設計往往偏于保守，如果對雙聯拱隧道結構進行合理的分析與優化，使其在滿足支護與使用功能的前提下能節約材料，減小建設成本，則具有較大的研究意義。

本次競賽圍繞雙聯拱隧道的工程背景，要求進行雙聯拱隧道結構模型設計與優化、建造與加載，使得隧道模型在用料盡量少的情況下能具有最大承載能力，尋求具有可行性、合理性和科學性的最優設計方案。賽題給定模型箱內部尺寸0.6m×0.8m×0.5m，雙聯拱隧道結構體系包括模型邊墻、中隔墻、襯砌及拱。模型設計要求采用盡可能少的白卡紙設計隧道結構，模型結構能達到最小變形及最大承載的效果，通過加載試驗檢驗整個隧道體系的承載力和變形特征，利用承載比指標評定隧道結構體系的穩定性。

2 有限元模型建立及工況設計

2.1 基本假定

設計方案總體上采用邊墻+中隔墻+襯砌+拱的結構形式，利用MIDAS-GTS建立三維隧道分析模型[1]。考慮到實際模型試驗中隧道結構體系各構件的連接方式與承載方式，以整體模型進行分析。

隧道襯砌采用單層白卡紙封層代替，邊墻采用4～5根立柱粘貼白卡紙封層代替，考慮到中隔墻的兩側無標準砂填充，因此以間隔排列的立柱代替中隔墻，中隔墻立柱與邊墻立柱以頂部圓弧形拱結構剛性連接。同時，為了保證邊墻立柱有足夠抵擋側向土壓力的能力，在模型底部考慮增加橫向支撐，橫向支撐與立柱剛性連接。有限元模型中構件剛性連接的假定雖與實際情況有偏差，但為便于模型制作，實際模型在這些位置處均采用白卡紙帶和膠粘貼固定，即使不是剛性連接，但在加載過程中構件節點處并未發生明顯相對位移，因此用剛性連接近似模擬。此外，所有構件均假定在彈性范圍內工作。

2.2 計算參數與計算步驟

2.2.1 模型計算單元

考慮到模型構件制作以中空的圓形及方形為主，因此，有限元模型里隔墻中的立柱及頂部拱均設置為中空的管形或方形構件，按一維梁單元進行分析，構件的外徑或邊長取10.0mm，內壁厚度2.0mm;單層白卡紙襯砌按二維板單元分析，其外輪廓與拱+邊墻立柱的外緣相貼合。模型外側的標準砂按三維實體建立模型，標準砂網格按照默認四面體單元生成，并且設置襯砌網格、立柱及拱的單元劃分與標準砂網格的節點重合。

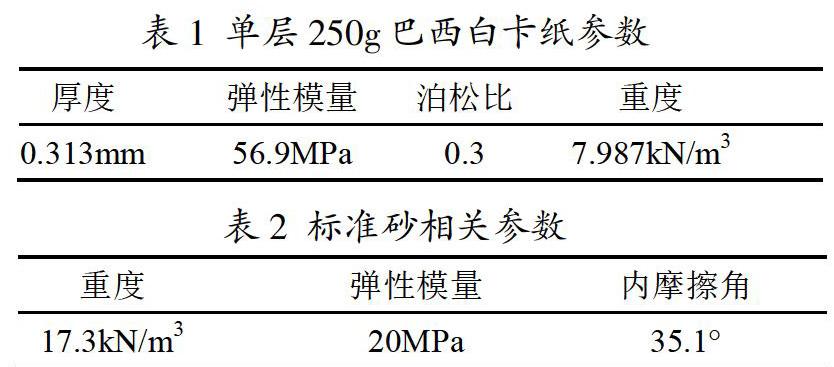
隧道結構模型制作涉及白卡紙和標準砂，材料參數取值[2-5]見表1和表2。

2.2.2荷載模擬

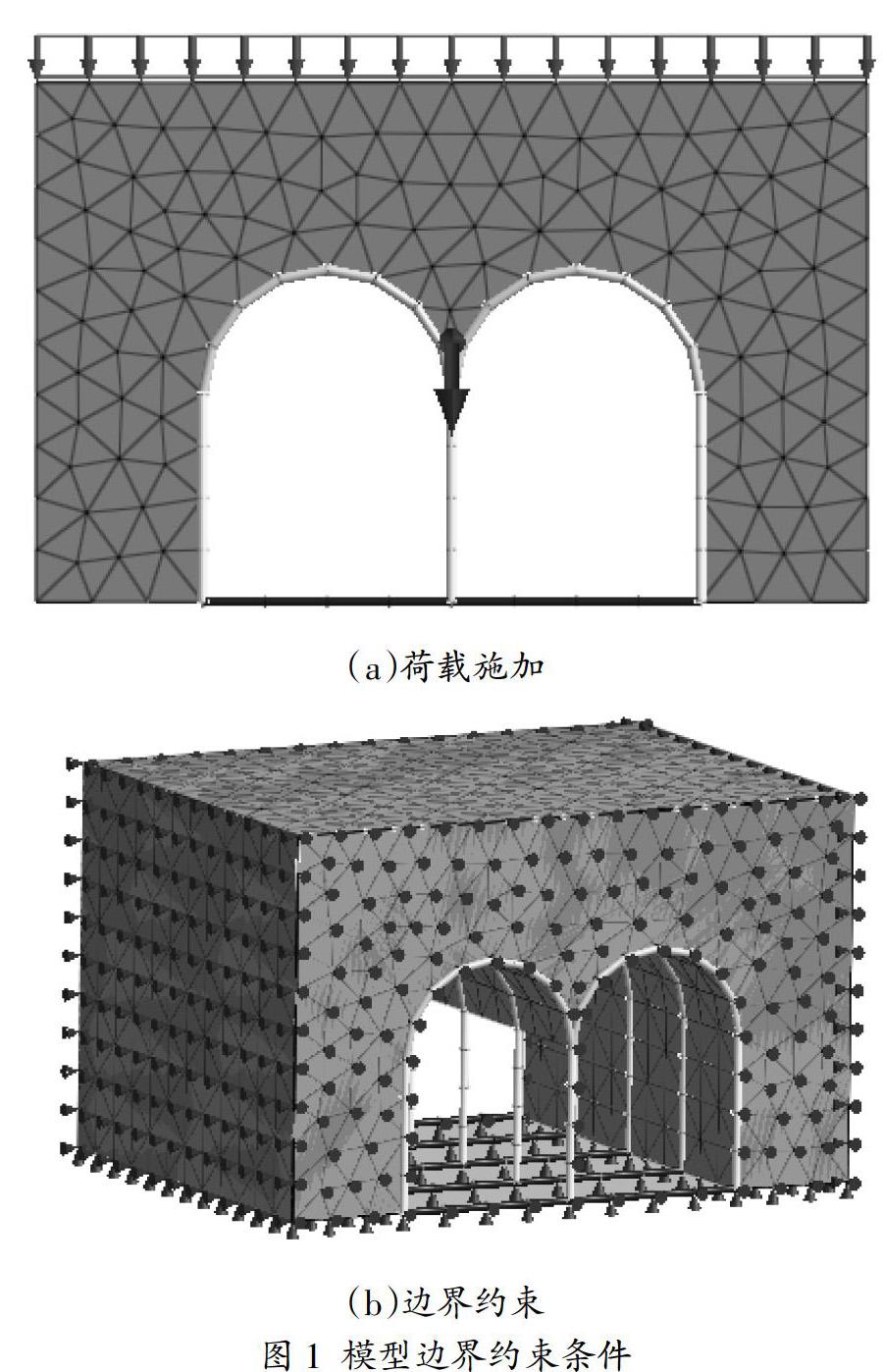
荷載分為自重荷載及加載荷載，按施工工況進行區分。建模時考慮標準砂自重及加載板均布自重0.5417kPa（26kg），最大加載荷載（200kg）簡化成均布壓力（4.17kPa）施加在加載板表面，如圖1（a）所示。標準砂及加載板自重按加載前施工工況處理，后續加載荷載按加載工況處理并且通過設置增量步加載得到分級加載的結果。

2.2.3 邊界約束

根據加載過程中標準砂的實際位移情況，在模型外邊緣節點位置設置位移約束條件。在標準砂與模型箱接觸的外側進行水平向位移約束，在標準砂底部進行豎直向位移約束，如圖1（b）所示。

2.2.4計算步驟

按下列步驟進行每一模型工況計算參數的輸入及模型分析。

材料屬性輸入→幾何模型生成→網格劃分擴展→結構單元析取→邊界荷載設置→施工階段定義→分析工況設置→分析結果處理。

按上述步驟模擬雙連拱隧道的模型加載試驗，并按照實際的試驗流程布置合理的施工階段，施工階段分為三部分：

（1）加載初始階段，施加模型自重，同時位移清零;

（2）放置加載板，施加加載板自重;

（3）砝碼加載，共分成10步荷載，每步20kg，直至200kg。

2.3 工況設計與計算結果

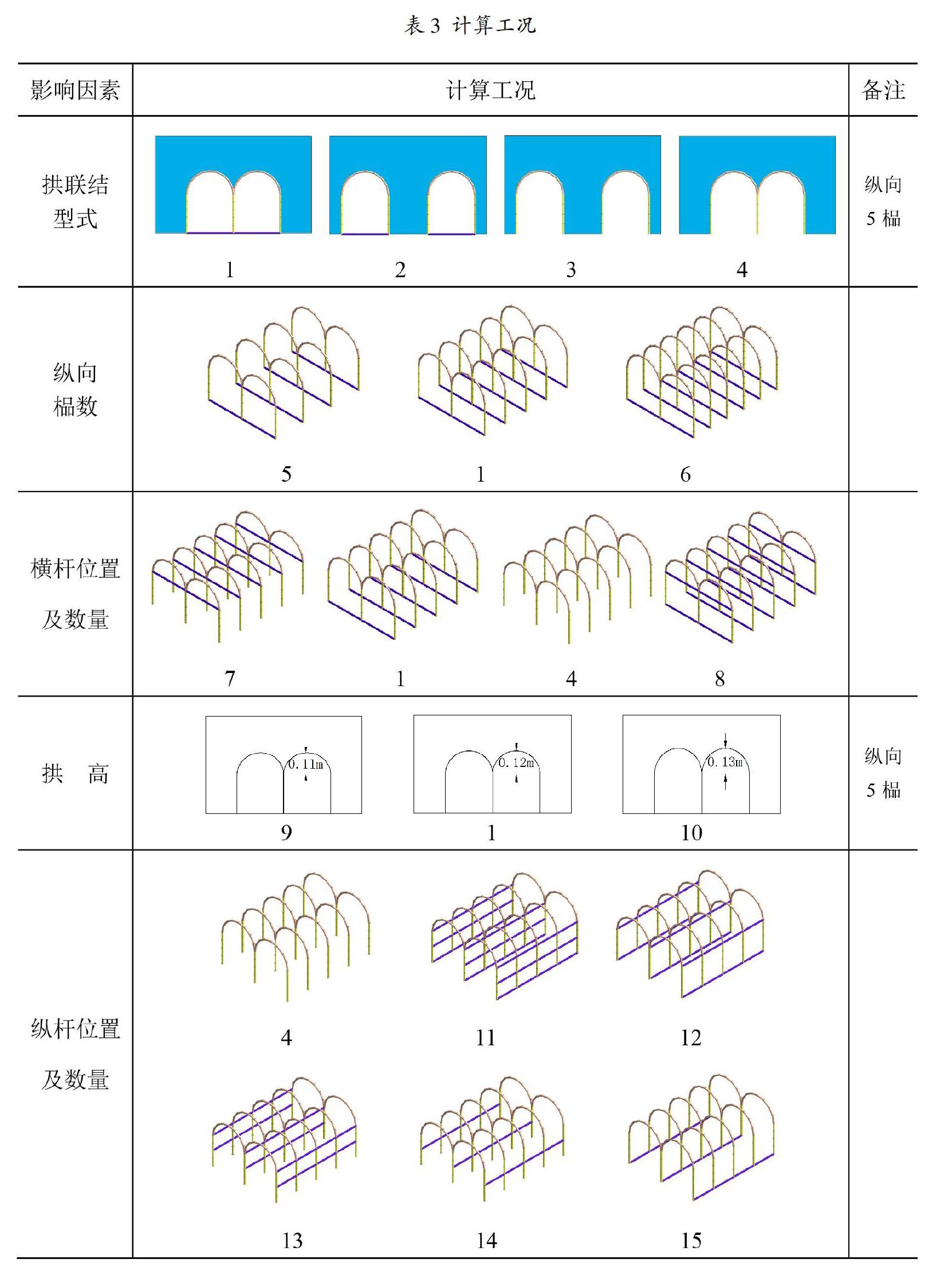
為了分析結構形式、構件數量、位置等因素對模型的影響，根據表3的工況分別建模計算，每一工況主要考慮實際模型制作中較重要的影響因素，如拱聯結型式、縱向榀數、拱高、橫桿位置及數量、縱桿位置及數量等。考慮到隧道物理模型與有限元模型本質上的諸多差異，物理模型與計算模型的結果實際上并不是很吻合，因此，工況分析時各影響因素對模型受力的影響主要做定性分析與比較，定量的結果，如位移、構件軸力等只是作為定性分析與比較的參照。通過各工況的計算，得到相對較合理的模型形式、構件的適宜數量及合理的布置方式，用于指導后續物理模型的制作。

根據有限元計算結果，匯總前述各工況下模型頂部豎向位移、構件最大側向位移及構件最大軸力，詳見表4。

3 結果分析

3.1 拱聯結型式

按照賽題要求，隧道兩側距離載箱距離不小于5cm，因此設計兩種聯拱聯結型式，工況1、4為兩個拱聯結在一起，中間以立柱代替隔墻，工況2、3為兩個拱分開設置，兩邊距加載箱距離為5cm。另外，工況1-4還考慮了拱底部設置橫向桿件的影響。四種工況下沉降平均位移和構件軸力見表4所示，在相同的最大加載量下工況1的沉降為3.07mm，拱分開布置的工況2的沉降為4.51mm，較工況1增加了約47%;工況4的頂面沉降為3.12mm，工況3的頂面沉降為6.05mm，較工況1增加了約94%。因此，根據計算結果，總體上拱底部無論是否設置橫桿，兩個拱聯結在一起的型式對于模型沉降控制效果較好。

構件受力方面，工況1、4最大軸向力出現在邊柱上，工況2、3最大軸向力出現在中柱上。工況1中最大軸向力約129.5N，工況2中最大軸向力約106.9N;工況3中最大軸向力約134.1N，工況4中最大軸向力約124.9N。因此，拱是否分開設置對模型構件最大軸力的影響大約在10%～20%左右，沒有對沉降的影響顯著。從縱向上看，幾種工況下，靠近模型箱的立柱受力相對于中間部分立柱要小，實際模型制作時存在優化空間。

此外，分別由工況1、4和工況2、3的結果對比可知，無論拱分開或聯結在一起，拱底部橫桿的設置對減少模型沉降具有一致的效果，尤其是拱分開設置時，對沉降抑制能達到34%;拱聯結在一起時，底部橫桿對構件最大軸力改善沒有明顯效果。

3.2 縱向榀數

在確定拱的橫向聯結型式后，縱向榀數量直接關系到模型承載能力及重量。工況1、5、6分別考慮了縱向4榀至6榀變化時模型整體受力情況。表4中的計算結果表明，模型的沉降量隨榀數增加而降低，榀數由4增加至6時，模型沉降量由3.44mm減小至2.17mm。隨著榀數的增加，最大軸向受力構件由中柱向邊柱轉移，而且最大軸向力反而略有增加。因此，增加縱向榀數雖然能降低模型的沉降量，但對構件的最大受力沒有改善，若實際模型采用5～6榀的結構需注意對中間邊柱的加強。

3.3 橫桿位置及數量

為防止模型加砂及加載過程中側墻發生較大位移的問題，在賽題允許的條件下可以考慮在邊柱與中柱構件間增加橫桿，形成整體框架結構。工況1、4、7、8考慮了橫桿數量及位置不同時模型的受力情況，其中工況1為隧道底部設置一道橫桿，工況4沒有設置橫桿，工況7在拱底設置一道橫桿，工況8分別在隧道底及拱底各設置一道橫桿。

由表4中工況1、4和工況7、8對比，結合數值模擬結果可以看出，相對于不設橫桿的工況4而言，橫桿的增設可以減小模型的沉降量，但降幅不大，單道橫桿最大降低約7%，增設雙道橫桿降幅約9.3%，且單道橫桿設置在拱腳的位置比設置在隧道底部對沉降控制的效果更好。橫桿對構件最大軸力的影響也是隨位置變化而不同，拱腳位置設置橫桿能較大幅度降低構件的最大軸力，即使是在拱腳設置單道橫桿，可以使立柱的最大軸力降低約27%。另外，拱腳部位橫桿的增加還會使邊柱中的最大軸向力向中柱轉移，對于實際模型采用拱腳加橫桿的形式要注意中柱的加強。

3.4 拱高影響

根據賽題要求，拱部為圓弧拱形或分段直線圓弧拱形，段數不得小于3段，隧道下部凈空的橫向間距（跨度）是24cm，因此，上部圓弧拱的正常半徑（拱高）為工況1中的12cm。為分析拱的矢跨比對模型受力的影響，拱的跨度統一取24cm，工況9、10分別將拱高調整為11cm及13cm，模型計算的部分結果如圖2所示。

結合工況1的結果可以發現，拱高從11cm增加到13cm的過程中，模型的沉降在拱高為12cm時最小（3.07mm），拱高為13cm時最大（5.11mm）;構件的最大軸力則隨拱高增加而增大，拱高為13cm時較拱高11cm最大軸力增加了11.3%。此外，由拱部受力可以看出，拱部的軸向力在拱高較低時以受拉為主，如圖2（a）所示;拱高增大后拱部的拉力逐漸向受壓轉化，軸向受壓區域增大，如圖2（b）所示，逐漸符合拱結構的承載特征。因此，實際模型制作時在沉降滿足要求的前提下應盡量增大拱高以充分發揮拱形構件的承載特點，且在承載力滿足的條件下對模型沉降最有利的拱形為半圓弧形。

3.5 縱桿位置及數量

縱向桿件設置在邊柱及中柱間，可以用于增強榀之間的整體性，并且設置在側墻部位的縱桿可以減緩模型加載過程中側墻的變形，有利于提高模型的整體性。為分析縱桿設置的數量及位置對模型受力的影響，按照工況11-15的設置建立隧道分析有限元模型，并且與不設置縱桿的工況4結果進行對比分析。工況11在拱腳部位、側墻與中墻中部、隧道底部分別設置三道縱桿;工況12在拱腳部位、隧道底部分別設置兩道縱桿;工況13在拱腳部位、側墻與中墻中部分別設置兩道縱桿;工況14、15分別在側墻與中墻中部、隧道底部位設置一道縱桿。

相對于不設縱桿的工況4，設置不同數量縱桿的工況11-15最大加載時豎向位移均有所降低，但降幅都不明顯，變化最大的是設置三道縱桿的工況11，降幅達到4.8%。設置三道縱桿與兩道、一道縱桿的模型位移量差異也不大，一道縱桿無論設置在隧道底部或側墻中部，其豎向位移均略大于兩道及三道縱桿。從縱桿設置的位置來看，兩道縱桿設置在拱腳及隧道底部與設置在拱腳及側墻、中墻中部沉降幾乎沒有區別;單道縱桿設置在隧道底部的模型沉降量略小于縱桿設置在隧道中部的情形。

此外，從構件最大軸力分布來看，縱桿的布置對模型受力影響有限，相對于不設縱桿的工況4，構件最大軸力變化最明顯的是工況13，約增加了3.4%，其余工況中構件最大軸力相差不大。因此，結合上述各工況下模型沉降的結果，可以認為縱桿的布置對模型的受力特征影響有限。實際模型實驗中，考慮到模型箱側壁對模型縱向的約束，縱桿發揮的作用不大，可以在隧道側邊的底部設置一些輕型構造桿件，達到防止底部漏砂的目的即可。

4 結論

（1）對于不同工況的計算結果雖然跟諸多因素有關，但通過對比分析，可以認為拱的聯結型式、橫桿設置、立柱數量及拱數量的增加對降低模型的沉降效果相對明顯，也有利于模型承載力的提高。在模型重量允許的條件下應合理優化拱聯結型式、立柱及拱數，建議模型實驗中采用雙拱聯結一起的型式并且縱向在四榀方案基礎上進一步優化加強。

（2）計算結果表明，拱的高度越高，對豎向荷載傳遞越有利，即可以將上部荷載較好傳遞到立柱上，但拱高增加既會增加封層用紙量也會增大拱自身的用紙量，對減輕模型質量不利。在模型實驗中，當拱的跨度確定時，可以盡量降低拱高，在承載力滿足的前提下實現模型減重。

（3）從立柱的受力分布來看，縱向靠近模型箱的立柱受力比中間部位立柱小，可以減少卷紙長度或減小截面以便減輕模型重量;橫桿的布置上，拱腳加設橫桿能優于隧道底部加設橫桿，但考慮到理論模型與實際模型之間仍存在一定的差異，特別是節點連接的剛性限制與實際模型不同，位移的計算結果會偏于保守，最終方案仍需要結合模型實驗進行選擇。

參考文獻：

[1]王海濤.MIDAS/GTS巖土工程數值分析與設計——快速入門與使用技巧[M].大連理工出版社，2013.

[2]儲信慶，計宏偉.灰底白板紙與白卡紙的彈性常數對比[J].包裝工程，2015（23）：48-52.

[3]劉承斌，王步宇，孫鳳鋼，等.結構設計大賽材料性能試驗[J].實驗室研究與探索，2007（10）：186-187+190.

[4]夏雨，周詩博，李靖，等.結構設計競賽中紙質桿件相關參數確定及極限承載力研究[J].力學與實踐，2016，38（6）：705-708.

[5]常海林，張旭欽，錢格軍，等.大學生結構設計大賽材料力學性能試驗研究[J].高等建筑教育，2017，26（5）：108-114.