對(duì)一道高考概率壓軸題的思考與拓展

汪 樂(lè) 張啟兆

近年來(lái)，高考數(shù)學(xué)試題正從能力立意到素養(yǎng)導(dǎo)向發(fā)展,同時(shí)，壓軸題不再拘泥于傳統(tǒng)的數(shù)列、導(dǎo)數(shù)等問(wèn)題,2019年高考全國(guó)卷Ⅰ理科數(shù)學(xué)的壓軸題就是一道概率題，本文就對(duì)這道概率壓軸題進(jìn)行分析與拓展．

1 原題呈現(xiàn)

例1(2019年全國(guó)卷Ⅰ) 為治療某種疾病,研制了甲、乙兩種新藥,希望知道哪種新藥更有效,為此進(jìn)行動(dòng)物試驗(yàn).試驗(yàn)方案如下:每一輪選取兩只白鼠對(duì)藥效進(jìn)行對(duì)比試驗(yàn).對(duì)于兩只白鼠,隨機(jī)選一只施以甲藥,另一只施以乙藥.一輪的治療結(jié)果得出后,再安排下一輪試驗(yàn).當(dāng)其中一種藥治愈的白鼠比另一種藥治愈的白鼠多4只時(shí),就停止試驗(yàn),并認(rèn)為治愈只數(shù)多的藥更有效.為了方便描述問(wèn)題,約定:對(duì)于每輪試驗(yàn),若施以甲藥的白鼠治愈且施以乙藥的白鼠未治愈則甲藥得1分,乙藥得-1分;若施以乙藥的白鼠治愈且施以甲藥的白鼠未治愈則乙藥得1分,甲藥得-1分;若都治愈或都未治愈則兩種藥均得0分.甲、乙兩種藥的治愈率分別記為α和β,一輪試驗(yàn)中甲藥的得分記為X.

(1) 求X的分布列;

(2) 若甲藥、乙藥在試驗(yàn)開(kāi)始時(shí)都賦予4分,pi(i=0,1,…,8)表示“甲藥的累計(jì)得分為i時(shí),最終認(rèn)為甲藥比乙藥更有效”的概率,則p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假設(shè)α=0.5,β=0.8.

(ⅰ) 證明: {pi+1-pi}(i=0,1,2,…,7)為等比數(shù)列;

(ⅱ) 求p4,并根據(jù)p4的值解釋這種試驗(yàn)方案的合理性.

2 思維障礙

許多同學(xué)一見(jiàn)到此題,就被“嚇住”了:文字信息多,數(shù)據(jù)多,做題的信心也就不那么足了!筆者分析主要會(huì)在如下5個(gè)方面存在問(wèn)題.

1) 審題時(shí)不會(huì)抓關(guān)鍵詞．如“若都治愈或都未治愈則兩種藥均得0分”,有部分學(xué)生將“若都治愈”忽略掉了,從而在計(jì)算P(X=0)時(shí)出現(xiàn)了錯(cuò)誤.

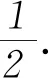
3) 數(shù)據(jù)分析的能力有待提高．如第(2)問(wèn)中給出了一些數(shù)據(jù),但部分同學(xué)不會(huì)分析,想不到利用第(1)問(wèn)的結(jié)論把a(bǔ)，b，c先求出來(lái),然后代入pi=api-1+bpi+cpi+1(i=1,2,…,7),從而得到0.5pi=0.4pi-1+0.1pi+1．

4) 缺乏解題經(jīng)驗(yàn)的積累．這種綜合題,通常“沒(méi)有白做的前一問(wèn)”,即前一問(wèn)常常為后一問(wèn)“鋪路搭橋”．由于缺乏這種意識(shí),第(2)問(wèn)(ⅱ)沒(méi)想到利用前一問(wèn)得到的pi+1-pi=p1·4i-1(i=0,1,2,…,7),從而無(wú)法聯(lián)想到“等差數(shù)列”和“累加法”,進(jìn)而不知道利用方程思想解決問(wèn)題．

5) 不會(huì)分析試驗(yàn)方案的合理性，特別是有些學(xué)生對(duì)概率的意義不理解． 在本題中，若不了解假設(shè)檢驗(yàn)的統(tǒng)計(jì)思想和基本概念，就不會(huì)根據(jù)p4的值解釋這種試驗(yàn)方案的合理性．

3 解法剖析

1) 閱讀理解, 尋求突破.

在閱讀過(guò)程中要學(xué)會(huì)抓關(guān)鍵詞．本題的關(guān)鍵信息有如下4點(diǎn).

a)當(dāng)其中一種藥治愈的白鼠比另一種藥治愈的白鼠多4只時(shí),就停止試驗(yàn),并認(rèn)為治愈只數(shù)多的藥更有效;

b)對(duì)于每輪試驗(yàn),若施以甲藥的白鼠治愈且施以乙藥的白鼠未治愈則甲藥得1分,乙藥得-1分;若施以乙藥的白鼠治愈且施以甲藥的白鼠未治愈則乙藥得1分,甲藥得-1分;若都治愈或都未治愈則兩種藥均得0分;

c)甲、乙兩種藥的治愈率分別記為α和β,一輪試驗(yàn)中甲藥的得分記為X;

d)若甲藥、乙藥在試驗(yàn)開(kāi)始時(shí)都賦予4分,pi(i=0,1,…,8)表示“甲藥的累計(jì)得分為i時(shí),最終認(rèn)為甲藥比乙藥更有效”的概率,則p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假設(shè)α=0.5,β=0.8.

第(1)問(wèn)的目標(biāo)是求X的分布列,因此先要明確:X表示一輪試驗(yàn)中甲藥的得分,X的取值有3種情況，即1，-1，0.得1分是施以甲藥的白鼠治愈且施以乙藥的白鼠未治愈,則P(X=1)=α(1-β);得-1分是施以乙藥的白鼠治愈且施以甲藥的白鼠未治愈,則P(X=-1)=(1-α)β;得0分是都治愈或都未治愈,則P(X=0)=αβ+(1-α)(1-β)．

第(2)問(wèn)(ⅰ)要證明: {pi+1-pi}(i=0,1,2,…,7)為等比數(shù)列;第(2)問(wèn)(ⅱ)求p4,并根據(jù)p4的值解釋這種試驗(yàn)方案的合理性.由于第(2)問(wèn)直接給了數(shù)列的遞推式,因此順著題目要求,利用題目中所給的“腳手架”,問(wèn)題就容易突破了．

2) 化歸整合, 提煉題目.

在閱讀過(guò)程中學(xué)會(huì)“翻譯”,把文字語(yǔ)言“翻譯”成對(duì)應(yīng)的數(shù)學(xué)語(yǔ)言．如:隨機(jī)分配一只小白鼠試驗(yàn)甲藥,隨機(jī)分配一只小白鼠試驗(yàn)乙藥(隱含的條件就是試驗(yàn)是獨(dú)立的),一輪試驗(yàn)共有4個(gè)可能出現(xiàn)的結(jié)果(每一個(gè)結(jié)果即為一個(gè)樣本點(diǎn))，如表1所示.

表1

(這里符號(hào)√,×分別表示治愈和未治愈)

又如:一輪試驗(yàn)會(huì)反復(fù)進(jìn)行,即獨(dú)立重復(fù)試驗(yàn),什么時(shí)候結(jié)束呢?如何將已知條件“當(dāng)其中一種藥治愈的白鼠比另一種藥治愈的白鼠多4只時(shí),就停止試驗(yàn)”翻譯為數(shù)學(xué)語(yǔ)言?

當(dāng)問(wèn)題比較抽象的時(shí)候,可以運(yùn)用特殊化法和枚舉法幫助我們理解題目，如表2所示．

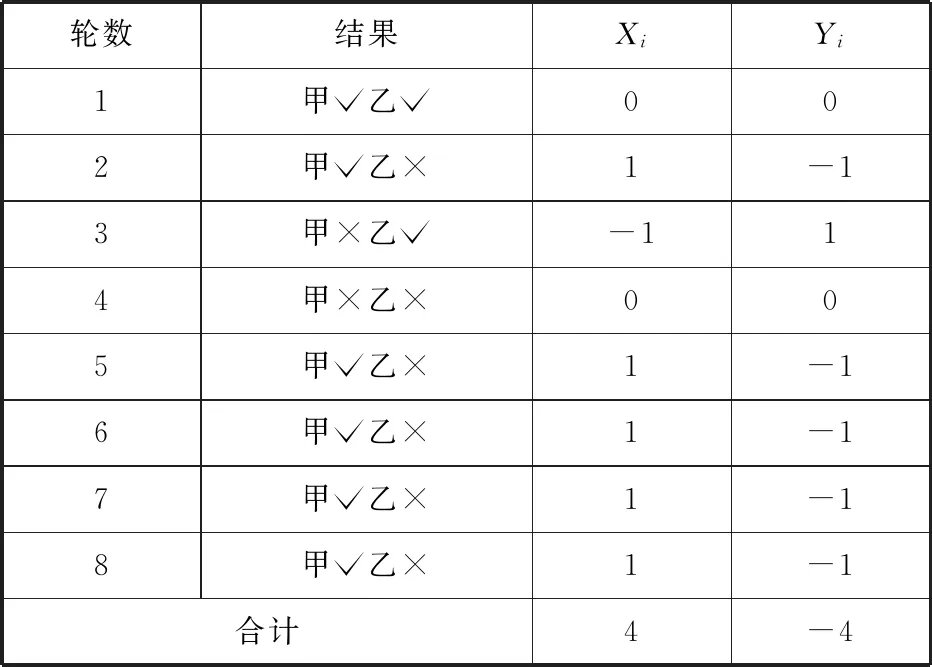
表2

從表2中,我們不難發(fā)現(xiàn)，因?yàn)閄i=-Yi,所以 ∑Xi=-∑Yi;當(dāng)且僅當(dāng)∑Xi=4 或-4時(shí)試驗(yàn)結(jié)束．這樣就把“當(dāng)其中一種藥治愈的白鼠比另一種藥治愈的白鼠多4只時(shí),就停止試驗(yàn)”翻譯為數(shù)學(xué)語(yǔ)言了．即當(dāng)∑Xi=4時(shí)，認(rèn)為甲藥更有效,當(dāng)∑Xi=-4時(shí)，認(rèn)為乙藥更有效．

3) 追本溯源, 梳理知識(shí).

通過(guò)聯(lián)想,找到與問(wèn)題信息相關(guān)的知識(shí)、解題技巧以及對(duì)相關(guān)數(shù)學(xué)符號(hào)、概念、命題等的理解,識(shí)別出問(wèn)題類型.如本題在分析已知條件后，需要聯(lián)想到隨機(jī)試驗(yàn)、獨(dú)立重復(fù)試驗(yàn)、離散型隨機(jī)變量的分布列及其概念,同時(shí)，要掌握證明等比數(shù)列的基本方法、數(shù)列的遞推關(guān)系等．

本題中試驗(yàn)的思路和各類比賽記分方法相似，以乒乓球比賽為例,甲、乙進(jìn)行乒乓球比賽,三局兩勝制.每局比賽中,如果甲至少得到11分且至少領(lǐng)先乙2分才能獲勝,也就是說(shuō)甲以11∶9，12∶10，13∶11，14∶12…比分領(lǐng)先才算獲勝．這里看的是凈勝球,不是得分比例．這道題題干中相當(dāng)于把甲至少得到11分且至少領(lǐng)先乙2分換成了甲至少得到4分且至少領(lǐng)先乙4分．有了這個(gè)模型,第(1)問(wèn)的解題思路就有了．

由第(2)問(wèn)(ⅰ)要聯(lián)想到數(shù)列的遞推關(guān)系和“差數(shù)列”模型,從而聯(lián)想到“累加法”,p4的值就容易求出了．

4) 水到渠成, 得出結(jié)論.

解析 (1)X的所有可能取值為1，-1，0.

得1分是施以甲藥的白鼠治愈且施以乙藥的白鼠未治愈,則P(X=1)=α(1-β);

得-1分是施以乙藥的白鼠治愈且施以甲藥的白鼠未治愈,則P(X=-1)=(1-α)β;

得0分是施以甲藥和施以乙藥的白鼠都治愈或都未治愈,則P(X=0)=αβ+(1-α)(1-β).

綜上，X的分布列如表3所示.

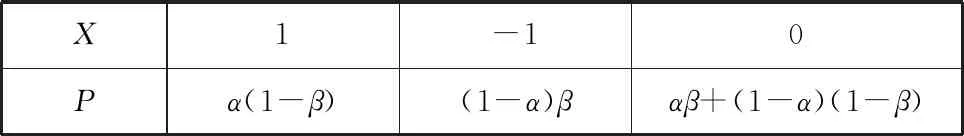
表3

(2) (ⅰ)因?yàn)棣?0.5,β=0.8,則

a=P(X=-1)=0.4,b=P(X=0)=0.5,
c=P(X=1)=0.1.

故可得pi=0.4pi-1+0.5pi+0.1pi+1,則

0.4(pi-pi-1)=0.1(pi+1-pi),

①

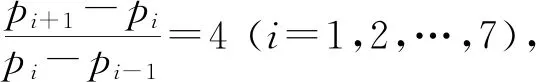
(ⅱ) 由(ⅰ)知,等比數(shù)列 {pi+1-pi}(i=0,1,2,…,7)的首項(xiàng)為p1,那么

p8-p7=p1×47,
p7-p6=p1×46,
…
p2-p1=p1×4.

以上式子兩邊同時(shí)相加,得p8-p1=p1×(47+46+…+4),則

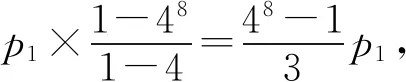
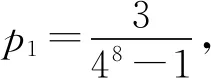
p4-p1=p1×(4+42+43),

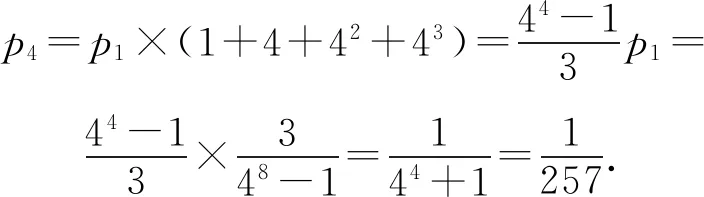
p4表示“甲藥治愈的白鼠比乙藥治愈的白鼠多4只,且甲藥的累計(jì)得分為4”，即最終認(rèn)為甲藥更有效的概率.

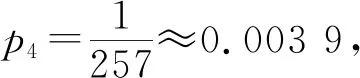
4 變式拓展

例2有人玩擲骰子移動(dòng)棋子的游戲,棋盤(pán)分為A,B兩方,開(kāi)始時(shí)棋子放在A方,根據(jù)下列規(guī)定移動(dòng)棋子:① 骰子出現(xiàn)1點(diǎn)時(shí),不能移動(dòng)棋子;② 出現(xiàn)2,3,4,5點(diǎn)時(shí),把棋子移向?qū)Ψ?③ 出現(xiàn)6點(diǎn)時(shí),如果棋子在A方,則不動(dòng),如果棋子在B方,則移至A方,將骰子擲了n次后,棋子仍在A方的概率記為Pn．

(1)求P1,P2;

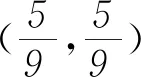
(3)求Pn．

解析 (1)P1為將骰子擲了1次后,棋子仍在A方的概率;P2為將骰子擲了2次后,棋子在A方的概率.

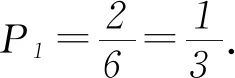
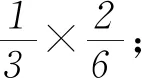
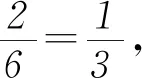
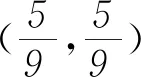
這兩道概率問(wèn)題將概率知識(shí)與數(shù)列知識(shí)有機(jī)結(jié)合,并且問(wèn)題貼近生活,體現(xiàn)出數(shù)學(xué)知識(shí)在解決實(shí)際問(wèn)題中的價(jià)值和作用.例1對(duì)高考復(fù)習(xí)具有導(dǎo)向作用,能看出高考數(shù)學(xué)壓軸題不再拘泥于傳統(tǒng)的數(shù)列、導(dǎo)數(shù)等問(wèn)題,凸顯出試題正從能力立意到素養(yǎng)導(dǎo)向轉(zhuǎn)變．因此,在今后的學(xué)習(xí)中,同學(xué)們不僅要重視“四基”(基礎(chǔ)知識(shí)、基本技能、基本思想、基本活動(dòng)經(jīng)驗(yàn)),還要重視數(shù)學(xué)知識(shí)和方法在解決問(wèn)題中的應(yīng)用,重視數(shù)學(xué)閱讀能力的培養(yǎng),提高解答實(shí)際數(shù)學(xué)問(wèn)題的能力.同時(shí)，要學(xué)會(huì)冷靜思考,順著問(wèn)題的要求進(jìn)行思考,思路中斷時(shí)不妨問(wèn)自己:“前一問(wèn)對(duì)后一問(wèn)有輔助作用嗎?”要學(xué)會(huì)利用題目本身為我們搭好的“腳手架”,學(xué)會(huì)拾級(jí)而上,就能以不變應(yīng)萬(wàn)變,在高考中取得理想成績(jī)．