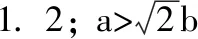應用橢圓中的焦點三角形為直角三角形解題

岳昌慶

本文中的焦點三角形指橢圓或雙曲線上一點P與兩焦點F1,F2所組成的△PF1F2.

關于焦點三角形的面積及內切圓的性質,已在拙文《淺議焦點三角形的內切圓》(《高中數理化》2016年第11期)及《淺議焦點三角形的面積》(《中小學數學(高中版)》2016年第11期)中做了相應的研究.本文僅討論當橢圓中的焦點三角形為直角三角形時,直角頂點在哪兒，需要滿足什么條件，并通過歷屆高考題對這一知識點的考查,得出一個一般性結論.

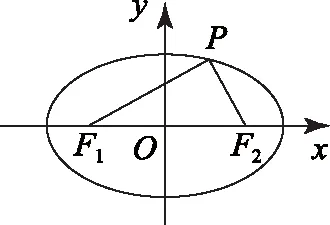
圖1

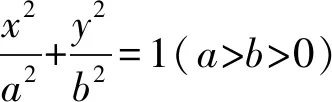
(1)若△POF2為等邊三角形,求C的離心率;

(2)如果存在點P,使得PF1⊥PF2,且△F1PF2的面積等于16,求b的值和a的取值范圍.

(2)由于16=b2tan 45°,所以b=4,c2=a2-16.設|PF1|=m,|PF2|=n,在Rt△F1PF2中,有∠F1PF2=90°,

m+n=2a,

①

m2+n2=4(a2-16),

②

由①得n=2a-m,代入②整理得

2)橢圓上滿足PF1⊥PF2的點P有時也被稱為“焦垂點”,見練習1.

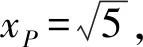
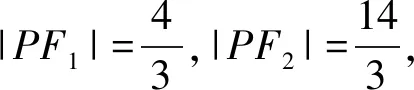
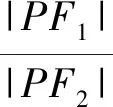
2)本題中的點P的坐標是可求的,若不加“|PF1|>|PF2|”的限制,本題點P的坐標應該有8解.類似題目,見本文練習2及練習3.

3)這類題目,如果命制巧妙,也可能出現點P的坐標有6解的情況,見練習4.

鏈接練習

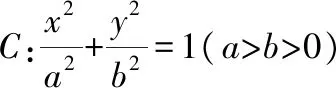
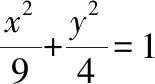
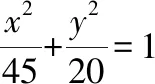
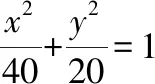
鏈接練習參考答案