傾斜界面耦合彈性層中的渡越輻射能1)

陜 耀 蘇 瓅 周順華

?(上海市軌道交通結構耐久與系統安全重點實驗室，上海 201804)

?(道路與交通工程教育部重點實驗室，同濟大學，上海 201804)

??(上海勘察設計研究院(集團)有限公司，上海 200093)

引言

物理學中，攝動源(perturbance source)在非均勻介質中或非均勻介質附近勻速直線運動所產生的能量輻射現象稱為渡越輻射(transition radiation).這一現象由前蘇聯物理學家Ginzburg 和Frank[1]在1946 年首次提出，他們分析了一個帶電粒子穿越理想導體和真空之間界面時所產生的電磁輻射.渡越輻射的早期研究即表明這一現象在不同物理場中普遍存在，包括電磁場[2]、光場[3]、聲波場[4]和彈性波場[5]等.產生這一現象的物理解釋為：物體在不同介質中運動時自身所攜帶的能量由于介質性質的不同而不同，在兩種介質界面處，這一能量差必須被平衡才能滿足介質連續條件，因此這一能量差獨立于物體運動而向兩側介質中自由傳播，產生的能量輻射現象即為渡越輻射現象.我國學者對渡越輻射的研究多集中在電磁學[6-8]和光學[9-12]領域.

Vesnitskii 和Metrikin[13]1992 年最早將渡越輻射引入力學分析，開始對移動載荷引起的彈性波在非均勻介質中傳播的渡越輻射現象進行研究.彈性波場中，一個勻速運動的點載荷經過非均勻的彈性介質界面時，介質中會產生能量輻射(該載荷運動速度應小于介質波速，以去除契倫科夫輻射等其他輻射的影響).為了探究軌道劣化和弓網接觸(受電弓和接觸網)劣化等問題的物理本源，從1996 年起陸續有學者[5]對列車載荷引起的彈性波在非均勻軌道和基礎中傳播的渡越輻射現象進行了理論分析.研究方法主要是將列車-軌道-路基系統理想化為一維或二維的物理模型，求解其位移場和應力場，通過位移場和應力場推導能量流動表達式，進而研究輪軌接觸彈性波在非均勻軌道和基礎中傳播產生渡越輻射能的流動規律.模型經歷了均勻彈性地基上的半有界弦/梁[5]、周期性/隨機非均勻彈性地基上的無限弦/梁[5]、兩個均勻各向同性半平面[14]和兩個均勻各向同性彈性層[15]的發展，如圖1 所示.而軌道和基礎的非均勻性(軌道幾何不平順和基礎剛度變化)集中體現在不同軌道基礎之間的過渡段(以高速鐵路路橋過渡段為例，如圖2 所示)，統計資料表明，過渡段軌道劣化速度顯著高于一般路基段和橋梁段.

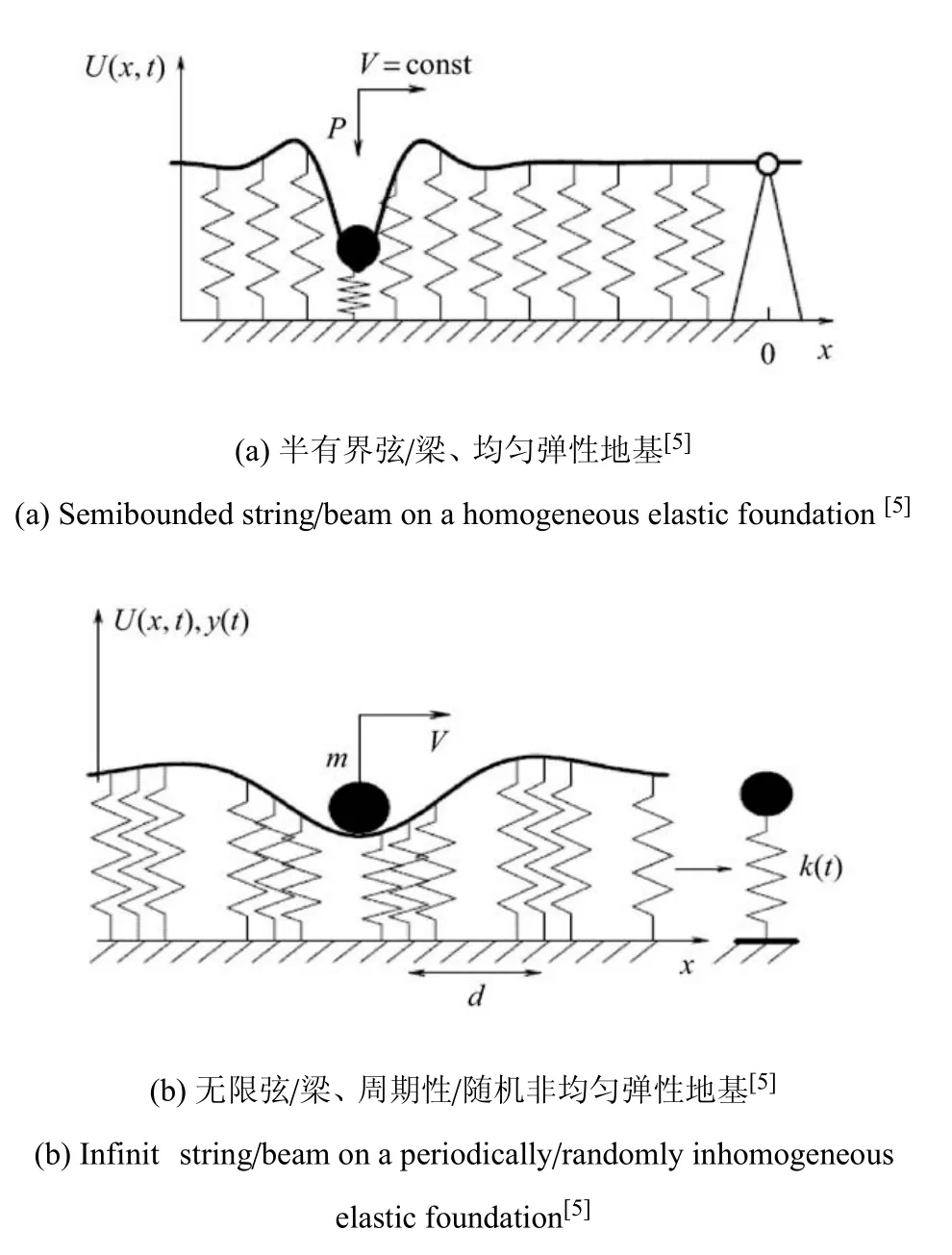
圖1 力學中的渡越輻射計算模型Fig.1 Transition radiation models in mechanics

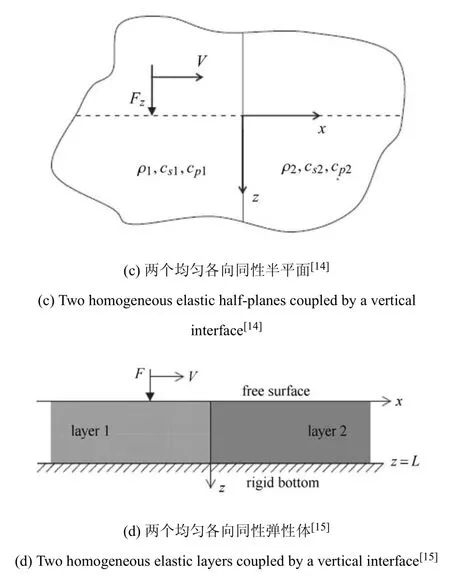
圖1 力學中的渡越輻射計算模型(續)Fig.1 Transition radiation models in mechanics(continued)

國內外對于過渡段動力特性的研究主要集中在現場實測、室內試驗和數值分析.以現場實測和室內試驗數據[16-22]為問題提出和理論驗證的依據，采用理論和數值模型[23-32]計算過渡段車輛-軌道-路基大系統各組成部分的動力響應，通過與現場實測或室內試驗所得數據的對比來驗證模型的可行性，進而分析過渡段剛度變化和軌道幾何不平順對列車運行平穩性和軌道各組成部分服役性能劣化的影響規律.現有的過渡段動力性能的數值分析多以研究對象動力響應的現象描述為主，其產生機理尚須從波動和能量的角度進行探索和研究.

Steenbergen 和Michael[33]從普遍物理力學概念角度指出：影響列車運行穩定性和軌道劣化的本源在于軌道的非均勻性.對于運行的列車，任何軌道組成材料或者幾何形位的變化都可以歸結為“非均勻”，輪軌接觸產生的彈性波在非均勻介質中傳播引起的渡越輻射是影響列車運行平穩性和引起軌道性能劣化的物理力學基礎.

軌道和基礎的非均勻性集中于不同軌道基礎之間的過渡段，以路橋過渡段為例(如圖2 所示)，橋臺與路基之間存在顯著的垂直界面和材料性質差異，過渡段路基沿線路縱向和深度方向均呈現典型的填料性質變化和成層分布，不同填料間水平和垂向界面明顯，車致彈性波在過渡段范圍內傳播將產生復雜的渡越輻射.渡越輻射現象會顯著放大軌道和基礎的應力場與應變場，造成軌道和基礎服役性能惡化，進而影響列車運行平穩性和旅客乘坐舒適度[15].以往關于波在非均勻彈性介質中渡越輻射的研究表明，擾動源運動速度越接近波在介質中傳播的速度，所產生的渡越輻射能越顯著.同理，隨著列車運行速度的不斷提高，當接近表面波(瑞利波)速時，既有過渡段結構引發的渡越輻射是否會加速過渡段服役性能的劣化？既有高速鐵路過渡段設計是否還能滿足長期穩定性的要求？

為回答上述問題，需要對既有高速鐵路過渡段渡越輻射能量流動規律和波場特征進行深入研究.

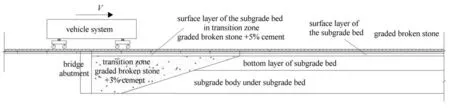
圖2 高速鐵路路橋過渡段結構[34]Fig.2 High-speed railway bridge-embankment transition zone configuratio [34]

為了研究過渡段復雜界面引起的車致彈性波渡越輻射能，需要建立通過復雜多界面耦合的介質振動模型(如圖3 所示).該理想模型的實現仍有很長的路要走，需要逐步厘清由垂直界面、傾斜界面和水平界面單獨存在引起的渡越輻射能，以及幾種界面共同作用的渡越輻射能.目前為止，既有研究已基本實現了通過垂直界面耦合的半無限彈性層模型[15](如圖1(d)所示)的構建.在此基礎上，后續研究應著重解決傾斜界面引起的渡越輻射問題，以及進一步分析垂直界面與傾斜界面共同作用下的渡越輻射問題.

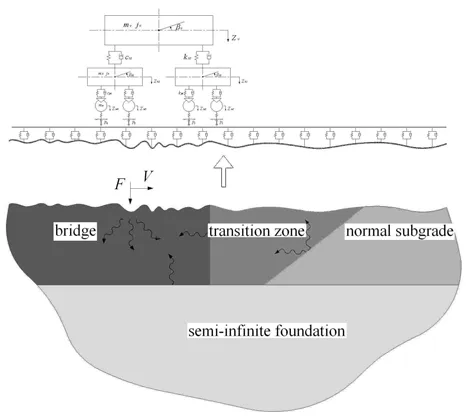
圖3 過渡段復雜多界面耦合振動模型Fig.3 Transition zone muti-interfaces coupling vibration model

本文在van Dalen 等[15]建立的由垂直界面耦合的兩個半無限均勻彈性層模型的基礎上，采用分離變量法求解了由傾斜界面耦合的兩個半無限均勻彈性層模型波動方程，并采用半解析方法對該模型中兩個彈性層中的渡越輻射能流密度進行了計算，分析了受載荷移動速度和界面傾斜角度影響的渡越輻射能流分布規律，以期對高速鐵路過渡段動力響應機理提供參考.

1 傾斜界面渡越輻射物理模型及數學模型

1.1 物理模型

高速鐵路路橋過渡段結構復雜，以我國《高速鐵路設計規范》(TB 10621—2014)[34]中推薦的倒梯形路橋過渡段結構為例，高速鐵路路橋過渡段中存在橋臺背與過渡段填料間垂直界面，基床表層與基床底層、基床底層與路基本體之間的水平界面以及過渡段填料與普通路基段之間的傾斜界面等多種不同剛度介質之間的界面.為理解高度鐵路路橋過渡段中的能流和波動特征，有必要對不同介質界面處產生的渡越輻射現象進行研究.van Dalen 等[15]給出了移動載荷經過兩個由垂直界面耦合的彈性層所激發的渡越輻射能的計算方法.為了進一步理解高速鐵路路橋過渡段中的波動及能量，本文中建立了分析由傾斜界面耦合的兩個半無限彈性層中渡越輻射現象的物理模型.

因高速列車經過引起的過渡段路基動變形處于彈性階段，可將過渡段路基各組成部分視為通過界面相互耦合的各向同性彈性體(小應變)，列車等效為沿自由面直線運動的集中載荷或質量塊.為分析過渡段波場特性，整個過渡段車輛-軌道-線下基礎系統抽象為如圖4 所示的物理模型.彈性層頂部為自由面，底部為剛性基礎，兩彈性介質由一傾斜界面耦合，在該界面處滿足位移、應力連續條件.該模型中坐標系為直角坐標系，x軸建立在自由面上，其正方向為移動載荷運動方向，z軸垂直于x軸，正方向從自由面指向剛性基礎.坐標系零點為介質1 與介質2 在自由面上的連接點.本文中將介質1 定義為移動載荷先經過的介質，介質2 定義為移動載荷后經過的介質.介質傾斜角度定義為介質界面與介質2 底部剛度基礎之間的夾角θ.

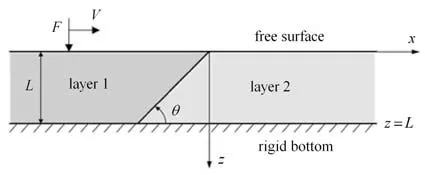
圖4 勻速運動載荷在兩種層狀介質傾斜界面處激發渡越輻射的物理模型Fig.4 Physical model for transition radiation excited by a surface load moving over an inclined interface of two elastic mediums

為分析兩種介質剛度差異產生的渡越輻射現象，移動的點載荷在兩種彈性介質表面勻速移動產生的彈性波場可被分解為本征場(eigenfield 和自由場(free field 兩個部分求解.本征場描述載荷本身在單一彈性介質中引起的波動響應，自由場描述由界面兩側介質差異引起的渡越輻射能場，兩者疊加成為可觀察到的總體彈性波場.本征場動力響應隨載荷移動，并局限于載荷一定距離范圍內，僅受到介質材料參數、載荷值大小及載荷移動速度影響.由于兩種介質的材料差異，在其界面處兩種介質中產生的本征場響應存在差值，即在同一空間坐標位置存在兩個不相等的動力響應值.而界面處兩種介質又需滿足位移應力連續條件，這一差異即可視為自由場的激擾源.自由場響應由界面向兩側介質中自由傳播，且獨立于載荷的運動，不僅受到介質材料參數、載荷值大小及載荷移動速度影響，同時也受到界面傾斜角度的影響.

1.2 數學模型

由斯托克斯-亥姆霍茲矢量定理可知，任何一個足夠平滑的矢量場都可以分解成無旋的部分和無散的部分.為描述1.1 節中物理模型的本征場及自由場彈性波，引入?(i),j，ψ(i),j兩個亥姆霍茲勢函數，其中?(i),j表示散度，ψ(i),j表示旋度.i={1,2}表示該勢函數所表征的介質層，j={e,f}分別代表本征場、自由場.兩個由傾斜界面耦合的彈性層中的彈性波場可由下述亥姆霍茲方程描述

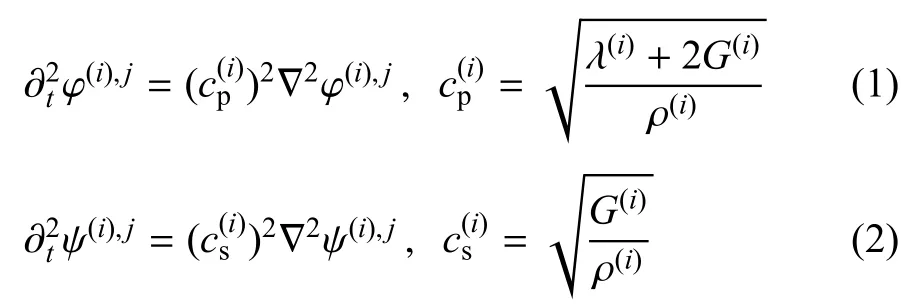
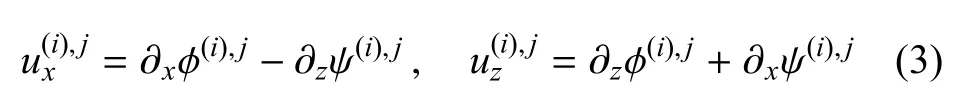
將點載荷經過x=0 的時刻定義為t=0，點載荷先經過的彈性層稱為介質1，后經過的彈性層稱為介質2，則模型的應力、位移邊界條件可由式(4)～式(8)表示

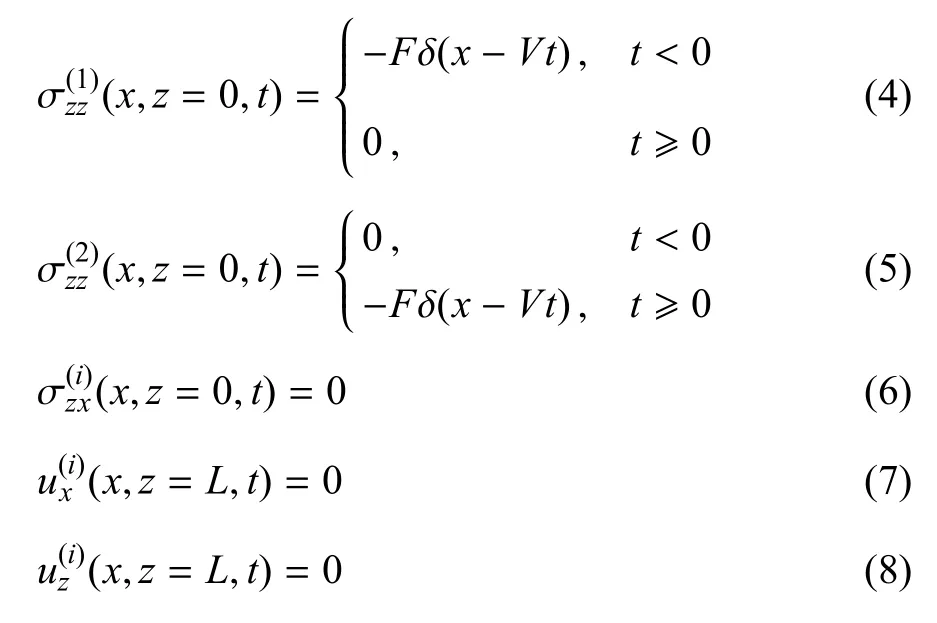
式中，i={1,2}分別表示介質1、介質2，L表示介質層厚度(如圖4 所示)，t表示時間，V表示點載荷移動速度，δ 為狄拉克函數.兩個介質層界面處位移應力應滿足式(9)～式(12)所示的連續條件.

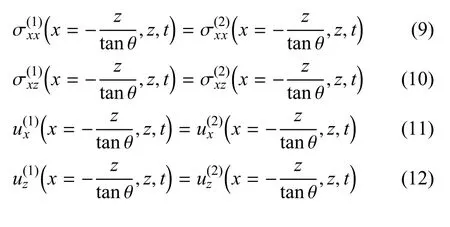
介質中的位移場、應力場均為本征場與自由場的疊加，即

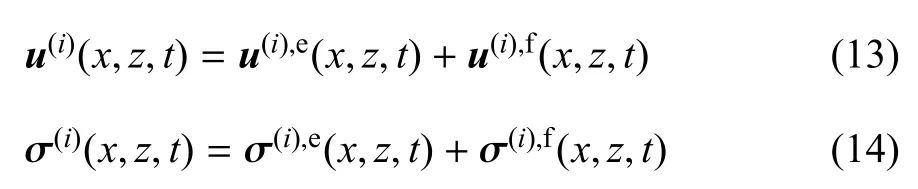
式中，上標e 表示本征場，f 表示自由場.

1.3 波動方程求解

將1.2 節中給出的亥姆霍茲方程作傅里葉變換，代入邊界條件中即可得到兩個彈性層各自的本征場波動方程頻域解.van Dalen 等[15]在其對垂直界面耦合彈性層中渡越輻射能的研究中給出了本征場的詳細求解過程，本文不再贅述.

自由場定義為由于點載荷所作用的彈性介質材料變化產生的彈性波輻射場，其激擾源為兩種不同材料介質在界面處的本征場動力響應差異.由于載荷作用在本征場中已經考慮，因此自由場的邊界條件中自由表面不再重復計算載荷作用，其邊界條件可表達如下

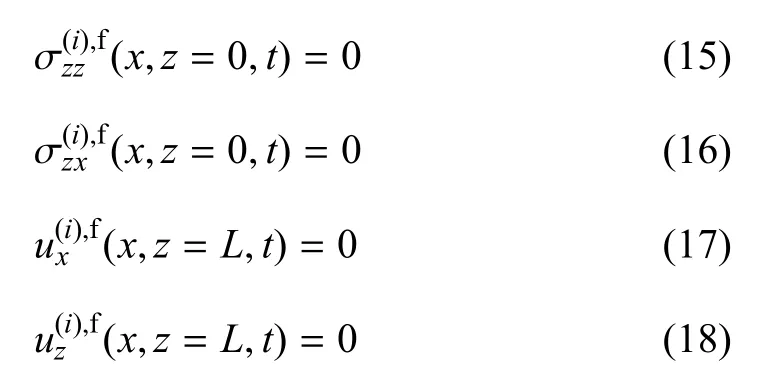
考慮本征場在介質界面處的響應差異為激擾源，自由場在介質中的傳播為彈性連續介質中的自由振動，其波動方程可采用分離變量法求解.在一個二維問題中，波動方程可分解為相互獨立的x相關項、z相關項和常數項.自由場可分解為無窮多組模態的疊加，每個模態對應一個唯一的水平向波數(介 質1)和(介 質2)，垂向壓縮波數(介質1)和(介質2)，垂向剪切波數(介質1)和(介質2)及模態參數(介質1)和(介質2).因此，求解自由場波動方程的關鍵是求解各模態一一對應的水平向波數和模態參數(垂向波數可由水平向參數直接轉化得到).式(19)～式(22)給出了頻域內模態疊加方法表達的自由場亥姆霍茲勢函數.

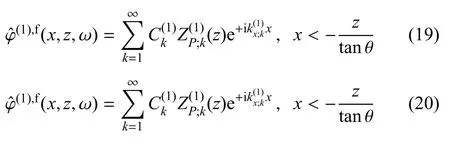
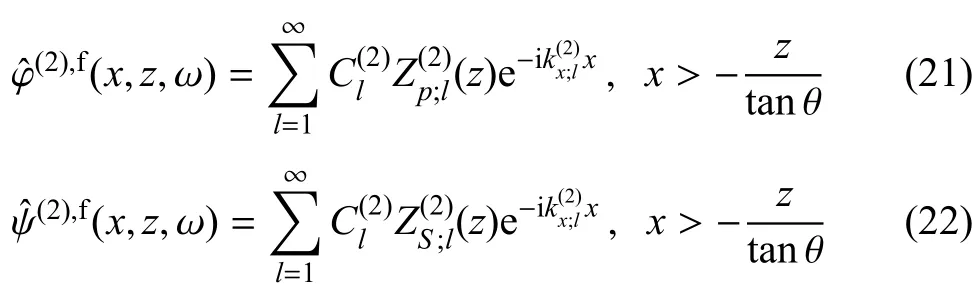
將以上4 式代入式(3)可得到自由場位移表達式，通過彈性介質應力-應變關系可以得到應力場表達.對于自由場位移應力，每個模態都應當滿足邊界條件要求，故將得到的表達式代入式(15)～式(18)可得如下等式

1.4 數值計算方法

由于自由場波動方程采用了分離變量法求解，波函數分解為無窮多個模態的疊加，難以通過純解析方法求解每個模態所對應的波數和參數.馬文濤等[35-37]均在研究中對二維彈性力學問題的數值求解方法做出了有益的貢獻.本文中對介質中自由場的響應亦采用數值方法求解，具體方法過程如下.

自由場波動方程在頻域內進行求解，由van Dalen[33]研究給出的結果可知，自由場渡越輻射能譜密度峰值均出現在10 Hz 以內，故本文頻域范圍均取為0～10 Hz，頻率步長取為0.1 Hz.對每一個頻率，為了得到介質中任意一點自由場位移值和應力值，均需要求解與模態一一對應的的水平向波數，Z相關項參數和模態參數.

求解的起點是1.3 節中給出的行列式為零的方程，該方程為復平面上的超越方程，本文中利用Matlab 內置函數fsolve 對數值求解，該算法原理為牛頓迭代法，這種算法需要給出初始值，算法在初始值附近范圍內尋找滿足條件的解.將的實部和虛部作為兩個獨立的未知數，經過試算將實部取值范圍設為?0.5～0.5，虛部取值范圍設為?16～0.實部初始值步長為0.02，虛部初始值步長為0.2，誤差范圍選取為1.0×10?8，即當行列式絕對值小于1.0×10?8時，認為該實部與虛部的組合為可接受的值.該方法計算得到的存在重復值.認為兩個解實部和虛部差值均小于1.0×10?6情況為重復解，僅保留其中誤差較小解.van Dalen 等[15]認為，自由場中選取100 個模態已經能較好地反映介質中的渡越輻射現象，且水平向波數虛部值越大的模態對渡越輻射能做出的貢獻越小.因此本文中將計算得到的水平向波數解按虛部值由大到小進行排序，僅保留前100 個解.將求解得到的水平向波數回代至頻散方程中求解方程組即得到了每個模態對應的Z相關項參數.

模態參數的求解涉及到了將每個模態計算得到的應力應變值對z進行積分的過程.對于每個算例的自由場計算均存在5 個積分項，且每個積分項均需要對介質1、介質2 不同模態組合及每個頻率進行積分，即對于一個算例為求解自由場模態參數需進行500 萬次積分，這一過程將極大地影響計算效率.因此，本文中將積分簡化為z方向上的求和，取計算步長為0.01，這一算法極大地提高了計算效率，且由于所取步長較短，積分算法與求和算法的計算精度差距不大，約為2‰～5‰.

模態選取量越多，自由場計算結果與理論解吻合度越高.本文計算條件下，選取100 個模態已能滿足模型界面處的位移應力連續條件.

2 渡越輻射能案例分析

渡越輻射能定義為兩彈性介質中向無限遠處傳播的能量，該范圍內能量傳播不再受本征場作用影響，因此這部分能量僅為自由場中的傳播模貢獻.渡越輻射能與介質中本征場應變能的比值表征了介質剛度變化對系統中能量分布的影響.

為計算自由場產生的輻射能通量，選取如圖5 所示閉合面Γ1，其水平邊界為介質自由面z=0 和介質剛性基礎z=L,其垂直界面為介質兩側x方向無限遠處，即|x|→∞.通過該閉合面的能通量可通過閉合面范圍內各點應力應變的乘積積分得到.

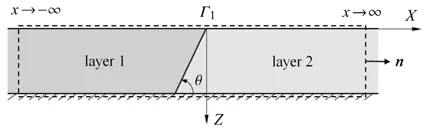
圖5 渡越輻射能通量計算閉合面Fig.5 Enclosing surface for accessing the energy flu associated with the transition radiation

2.1 計算參數

為研究載荷移動速度和界面傾斜角度對彈性層中能流密度分布的影響，本節中采用的載荷移動速度為20～ 90 m/s(間隔取10 m/s)，界面傾角為15?，30?，45?，60?，90?，120?，150?共14 種情況下界面兩側介質中的渡越輻射能.頻域計算范圍均為0～10 Hz，步長均為0.1 Hz，自由場均選取100 個模態進行計算.這里再次說明，本文中介質1 均定義為載荷先經過的介質，介質2 定義為載荷后經過的介質，界面傾斜角度定義為介質界面與介質2 剛性基礎之間的夾角θ.

所有算例中介質1 材料為材料A，介質2 材料為材料B，具體材料參數見表1.介質層厚度均為25 m.載荷移動速度改變的8 個算例中界面傾角均取為60?，界面傾斜角度改變的算例中載荷移動速度均取為50 m/s，移動載荷取值均為10 kN/m.

表1 材料參數表Table 1 Material parameters

2.2 載荷移動速度對渡越輻射能的影響

本文載荷移動速度的取值控制在介質臨界速度以內，以防止其他類型輻射(例如，切倫科夫輻射)的產生對渡越輻射受現象的干擾，因此，載荷移動速度取值為20～90 m/s(該案例分析中介質介質1 臨界速度為121 m/s，介質2 臨界速度為106 m/s).在載荷移動速度增大的過程中，渡越輻射能譜密度分布變化規律相似，且當載荷移動速度逐漸接近臨界速度時，渡越輻射能譜密度變化量值過大，難以在同一坐標尺度內表現能譜密度分布規律受到載荷移動速度的影響，因此，本節采用載荷移動速度為20，30，40 m/s 的計算結果來反映載荷速度變化對渡越輻射能譜密度分布規律的影響，如圖6 所示.能量譜密度中的特征頻率主要來源于水平向波數為實數的模態，故復波數為實數解的模態較多的頻率將計算得到較大的能量譜密度，主要受界面傾斜角度、介質剛度差異的影響.隨著載荷移動速度增大，渡越輻射能譜密度峰值點對應的頻率位置并未發生變化，但峰值并不是單調增大的.頻率較小范圍內(在該算例中為小于8.5 Hz)應變能譜密度隨著載荷移動速度的增大而增大，而頻率較大范圍內應變能譜密度峰值隨著載荷移動速度的增大有所下降.對整個頻域而言，可以認為隨著載荷移動速度的增加渡越輻射能譜密度向較小頻率內集中.介質2 中應變能譜密度最大值顯著大于介質1，但介質1 中峰值點較多，應變能密度在頻域上的分布較介質2 更均勻.

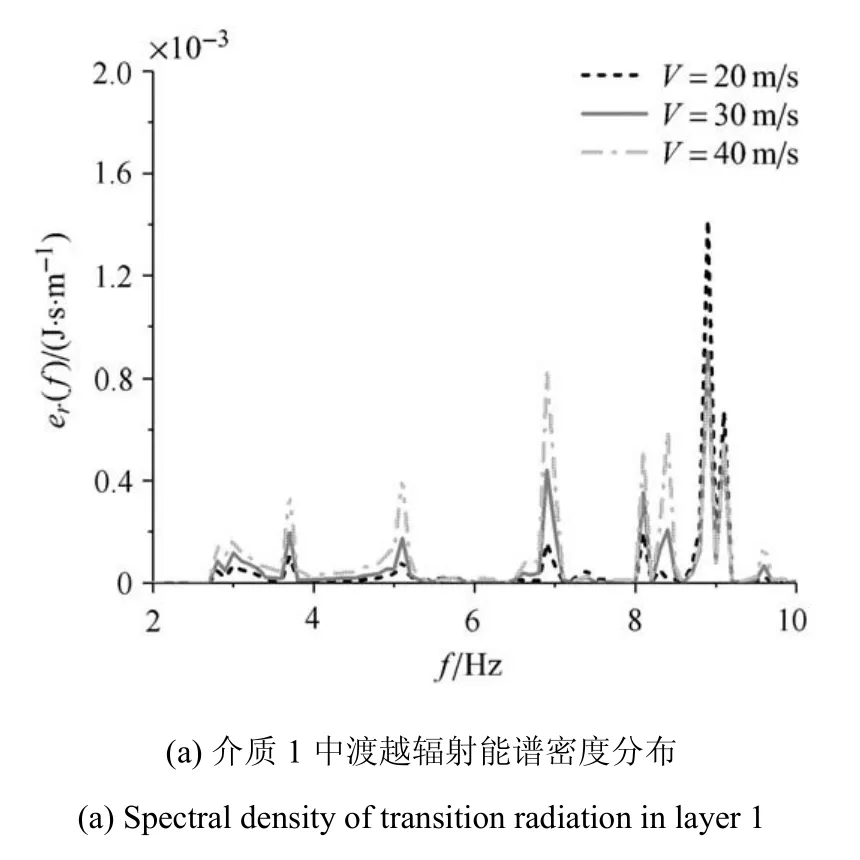
圖6 渡越輻射能譜密度隨載荷移動速度變化規律Fig.6 Spectral density of transition radiation with different load moving velocities

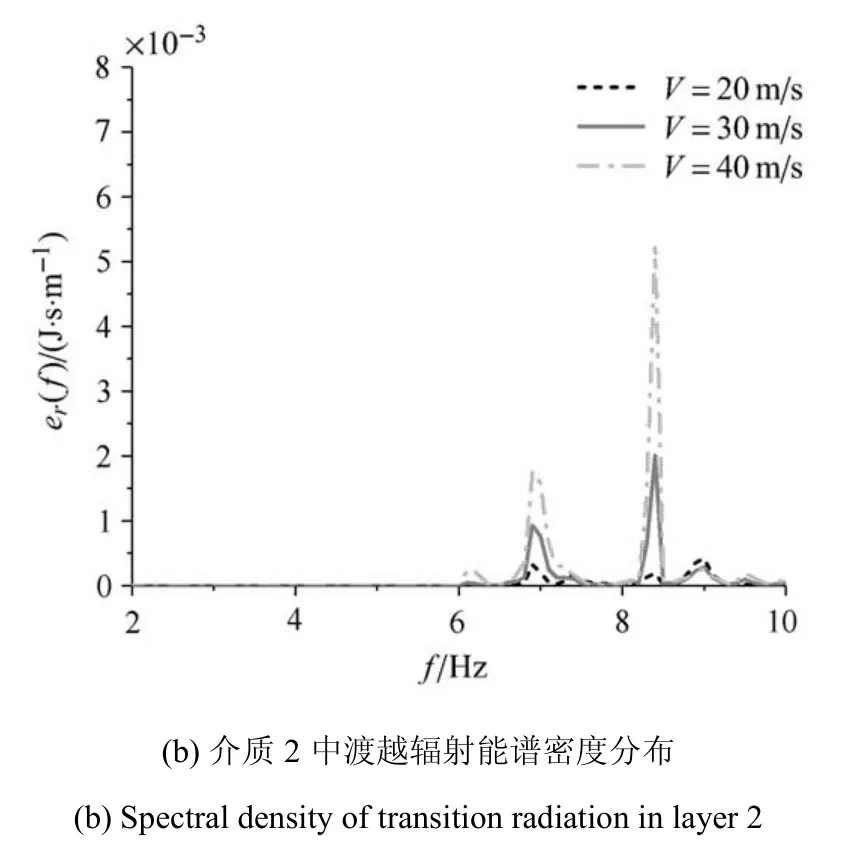
圖6 渡越輻射能譜密度隨載荷移動速度變化規律(續)Fig.6 Spectral density of transition radiation with different load moving velocities(continued)

圖6(a)與圖6(b)對比可知，隨著載荷移動速度的提升界面兩側介質中能量密度峰值差異減小.介質1 中隨載荷移動速度增大應變能譜密度向頻率較小側集中，介質2 中3 個應變能峰值點始終在頻率為6.2，6.9 和7.4 Hz 位置處，但三者之間的大小關系發生了變化，隨著速度的增大，頻率較小位置譜密度的增大幅度要大于頻率較大位置.

如表2 所示，載荷移動速度較小時，渡越輻射能譜密度峰值并不隨速度單調增大.當載荷移動速度超過50 m/s 后，渡越輻射能譜密度峰值隨載荷移動速度增大而單調遞增，且變化率也逐漸增大.當速度由80 m/s提升至90 m/s，兩側介質中渡越輻射能譜密度最大值增長率均發生顯著增長.介質1 中速度為80 m/s 時譜密度最大值僅為速度為90 m/s 時的13%，介質2 中該比值為26%.將得到的渡越輻射能譜密度分布對頻率積分可得到介質中向無限遠處傳播的渡越輻射能Er.

為理解渡越輻射現象對總能流密度分布的影響，將計算得到的渡越輻射能Er除以該算例參數下本征場應變能Ee，得到的比值稱為正規化的渡越輻射能.雖然介質2 中渡越輻射能較大，但由于其介質剛度較小，本征場應變能遠大于介質1 中本征場應變能，故介質2 中渡越輻射能對總能量場的貢獻比介質1 小.介質1 中渡越輻射能在載荷移動速度提升到80 m/s 以上時超過本征場應變能.圖7 中為正規化后的渡越輻射能隨載荷移動速度的變化規律，由圖可知隨著載荷移動速度的增大，兩側介質中渡越輻射能對總能量場做出的貢獻均單調非線性增大.本算例中，介質1 臨界速度為121 m/s，介質2 臨界速度為106 m/s，如圖7 所示，載荷移動速度達到界面介質2 臨界速度74%時渡越輻射能的絕對值大小已經超過了本征場應變能.對于高速鐵路列車而言，這一結論表明當列車行駛速度接近基礎臨界速度時，基礎剛度差異引起的系統動力響應可能會超過列車載荷本身激發的系統動力響應.

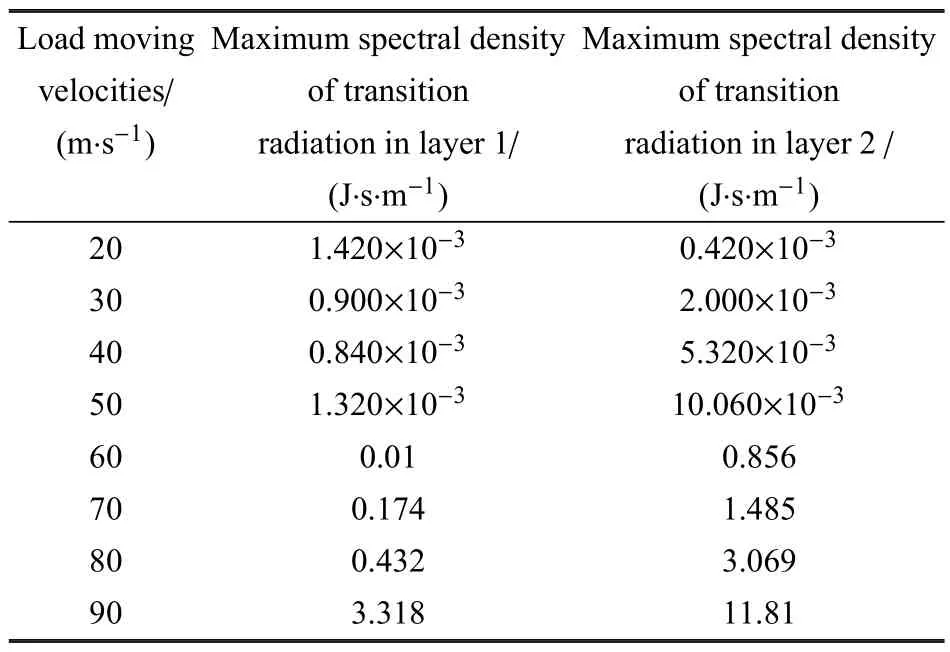
表2 自由場遠場應變能計算結果匯總Table 2 Summary table for the free fiel strain energy calculation results

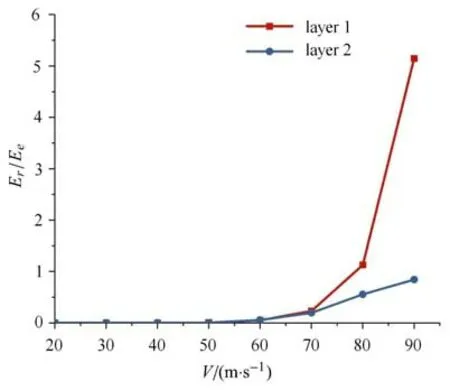
圖7 渡越輻射能與本征場應變能比值隨載荷移動速度變化規律Fig.7 Transition radiation energy normalized by the eigenfiel energy versus velocity V

2.3 界面傾斜角度對渡越輻射能的影響

圖8 中為不同界面傾角θ(界面與介質2 剛性基礎夾角)情況下兩側介質中的渡越輻射能譜密度分布，由于篇幅限制僅給出界面傾斜角度為45?，60?，90?，120?情況下的計算結果.對于界面傾角為銳角的情況，介質2 中的渡越輻射能譜密度最大值均大于介質1 中的最大值，且介質2 中渡越輻射能譜密度均集中于2～3 個峰值點.對于界面傾角為鈍角的情況，介質1 中的渡越輻射能譜密度最大值均大于介質2 中最大值，兩側介質中渡越輻射能譜密度均集中于頻率較大的范圍內.圖8(c)為界面為垂直情況下兩側介質中的渡越輻射能譜密度，界面垂直情況下，兩側介質的剛度差異成為影響介質中自由場譜密度分布的支配性影響因素，因此剛度較小的介質(介質2)中渡越輻射能顯著大于剛度較大介質(介質1).

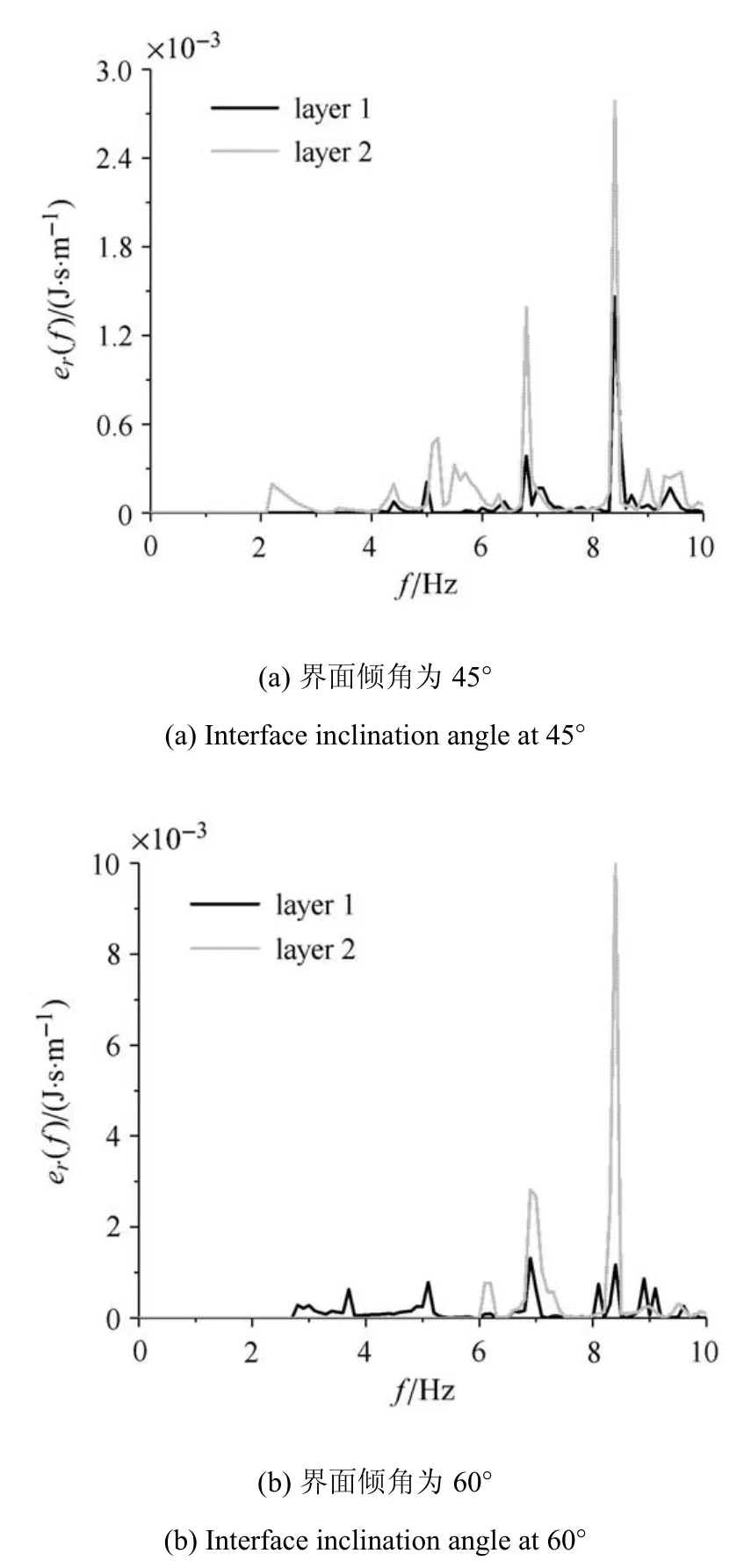
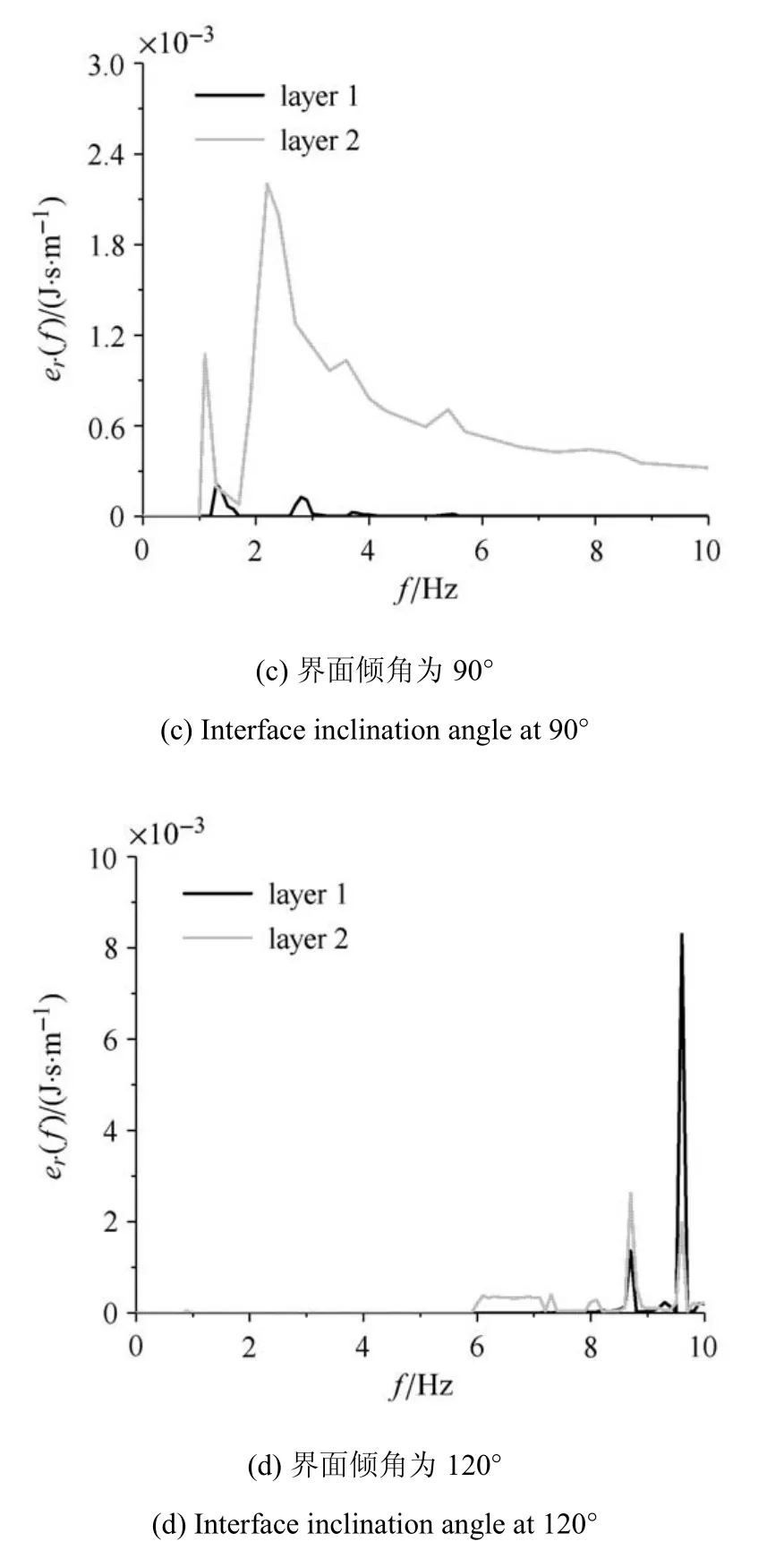
圖8 渡越輻射能譜密度隨界面傾斜角度變化規律Fig.8 Spectral density of transition radiation with different interface inclination angles

渡越輻射能譜密度譜密度最大值隨界面傾斜角度的變化規律并不是單調的.界面傾角為銳角情況下，介質2 中應變能譜密度峰值顯著大于介質1.界面傾角由45?增大到60?，介質1 中渡越輻 射能譜 密度峰值從1.460×10?3J·s/m 減 小至1.320×10?3J·s/m，介質2 中渡越輻射能譜密度峰值從2.780×10?3J·s/m 增大至1.006×10?2J·s/m.界面傾角為鈍角情況下，介質1 中應變能譜密度峰值顯著大于介質2.將渡越輻射能譜密度分布對頻率積分可得到介質中向無限遠處傳播的渡越輻射能，界面傾角為銳角情況下，兩側介質中渡越輻射能均隨界面傾斜角度單調增大，且介質2 中渡越輻射能始終大于介質1中渡越輻射能.

圖9 中為界面傾角為銳角情況下渡越輻射能對總能量場貢獻隨界面傾斜角度的變化規律.隨著界面傾斜角度的增大，兩側介質中渡越輻射能對總能量場做出的貢獻均單調非線性增大.界面傾角為銳角情況下，界面傾斜角度的增大對兩側介質中渡越輻射能貢獻相對大小關系沒有顯著影響.界面為垂直情況下，兩側介質中渡越輻射能對總能量場做出的貢獻的相對關系主要受到兩側介質剛度相對大小的影響.垂直界面情況下兩側介質中渡越輻射能的差異遠大與傾斜界面情況，其中剛度較小介質(介質2)中渡越輻射能對總能量場做出的貢獻大于傾斜界面情況，剛度較大介質中渡越輻射能對總能量場做出的貢獻小于傾斜界面情況.界面傾角由銳角變為鈍角，介質1 中渡越輻射能貢獻大于介質2.對于高速鐵路路橋過渡段設計而言，這一結果表明過渡段界面的傾斜有利于減小基礎剛度差異所導致的系統動力響應.

圖9 渡越輻射能與本征場應變能比值隨界面傾斜角度變化規律Fig.9 Transition radiation energy normalized by the eigenfiel energy versus interface inclination angle

3 界面附近近場應變能密度計算結果

將兩介質界面附近范圍內的應變能定義為近場能量，該范圍內自由場和本征場仍存在疊加，故需要考慮總的位移和應力場.該部分能量計算結果主要用于評估應變能的方向性和自由場在總場中的占比.因此，選取圖10 中的半圓形閉合面進行分析，本節計算中閉合面半徑R均選取為介質層厚度L的1/4，即6.25 m，其他計算參數與2.1 節中相同.本節中計算得到的介質1 中近場應變能均為負值，表明能量由閉合面外側向閉合面內側流動，這是由于近場能流密度中本征場能流密度占支配比例，而載荷由介質1 向介質2 移動，本征場能量由介質1 向界面處再向介質2 方向傳遞，因此介質1 中能流密度指向閉合面內側，介質2 中指向閉合面外側.

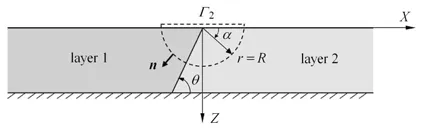
圖10 界面附近近場應變能通量計算閉合面Fig.10 Enclosing surface for accessing the energy flu close to the interface

3.1 載荷移動速度對近場應變能密度的影響

載荷移動速度對近場能量密度的方向性具有顯著影響.圖11 中為載荷移動速度分別為20 m/s和90 m/s 時的近場能量密度分布.由圖可知，載荷移動速度較小時，界面向主要向x軸兩側方向傳播能量，載荷移動速度較大時，沿界面方向傳播的能量較大.

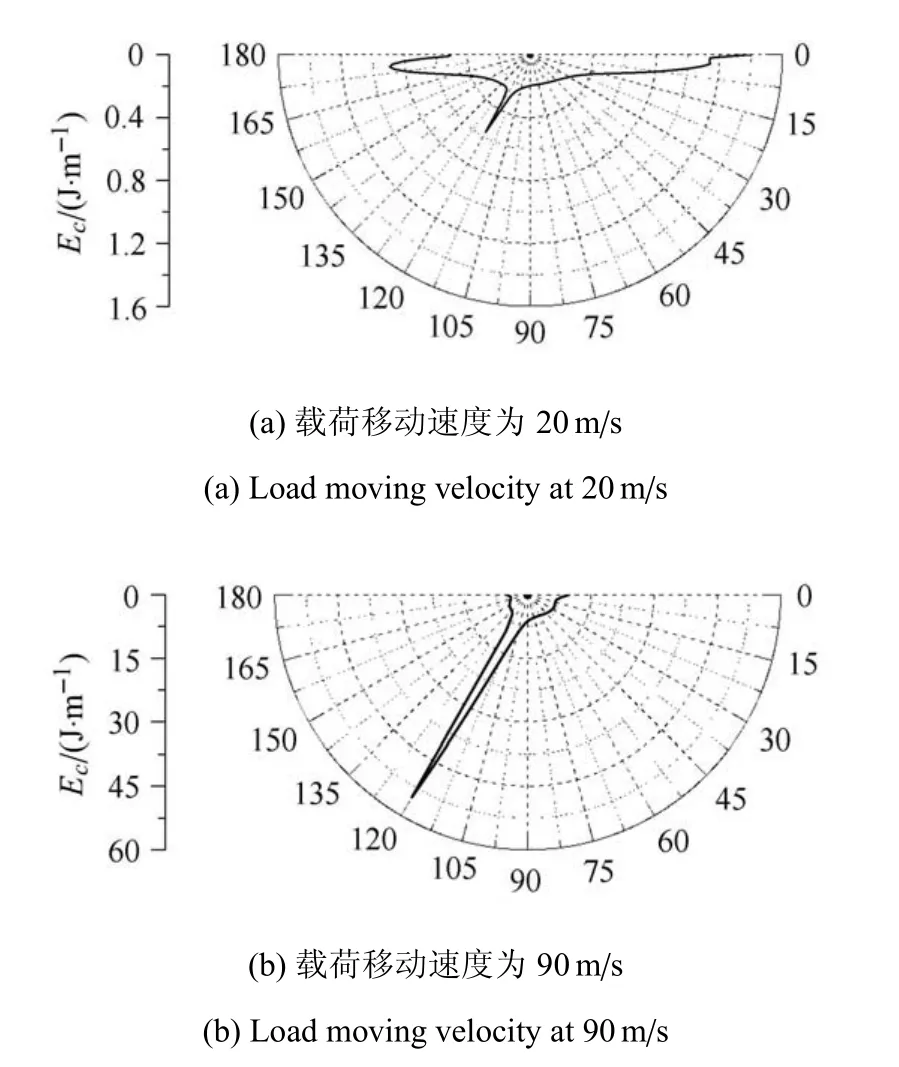
圖11 近場應變能角密度隨載荷移動速度變化規律Fig.11 Angular energy density of the near-fiel with different load moving velocity

近場應變能角密度隨載荷移動速度增大單調非線性增大.與遠場能量密度規律相同，近場應變能角密度在載荷移動速度達到90 m/s 時也發生了極大增長，速度為80 m/s 時的近場應變能角密度最大值僅為速度為90 m/s 時的24%.

相較于遠場渡越輻射能，近場應變能角密度在極坐標上的分布隨影響因素的變化規律相對不顯著，這是因為在界面附近范圍內本征場與自由場仍存在疊加，體現出的近場應變能不能獨立的反映自由場的能量輻射規律.因此，有必要計算自由場在近場應變能中所占的比例.

隨著載荷移動速度的增大，自由場在近場應變能中的占比逐漸增大.速度為20 m/s 時，自由場做出的貢獻主要沿界面方向，而速度為90 m/s 時，雖然自由場貢獻最大方向仍為沿界面方向，但其他方向自由場貢獻均有上升.載荷移動速度為90 m/s 時，介質1 中自由場對近場應變能密度的貢獻顯著大于介質2.

3.2 界面傾斜角度對近場應變能密度的影響

界面傾斜角度顯著影響了近場應變能密度在角度上的分布規律.圖12 及圖13 中不同界面傾角的模型均在極坐標系中沿兩介質界面方向的角度上出現尖點，這一結果表明最大近場應變能角密度均發生在介質界面方向上，即近場應變能中較大一部分能量是沿著兩介質界面方向傳播的，在介質界面位置通過兩介質之間的能量傳播平衡了移動載荷在不同介質中的能量差.介質1 中近場應變能密度隨介質傾角無明顯變化規律，但介質2 中存在介質傾角越大，近場應變能密度越大的規律.與遠場渡越輻射能規律不同，近場應變能角密度最大值并不隨介質傾角增大而單調增大，這可能是對于界面傾角為15?和30?的情況，界面距離自由表面距離較近，本征場在這一范圍內做出了較大貢獻.

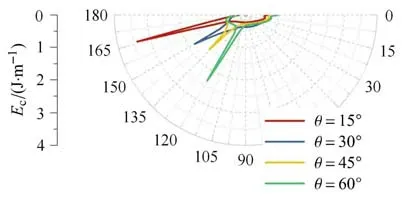
圖12 近場應變能角密度隨界面傾斜角度變化規律Fig.12 Angular energy density of the near-fiel with different interface inclination angle

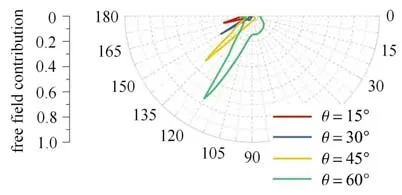
圖13 近場應變能角密度中自由場貢獻比例隨界面傾斜角度變化規律Fig.13 Free fiel contribution of near-fiel angular energy density with different interface inclination angle

自由場占近場應變能角密度比例在極坐標上的分布規律也與這一解釋相符，圖中不同界面傾角情況下仍為沿界面方向自由場占比最大，但最大值隨界面傾角的增大單調增大，這意味著界面傾角為15?情況下沿界面方向出現的能通量峰值主要由本征場貢獻.

4 結論

本文提出了傾斜界面耦合彈性層渡越輻射能分析模型，將介質中的動力響應場分解為本征場和自由場兩個部分，對自由場波動方程采用分離變量法求解，得到了本征場和自由場位移應力表達式.通過半解析計算得到了不同影響因素對介質中渡越輻射能流密度的影響規律：

(1)隨著載荷移動速度的增大，渡越輻射能單調非線性增大，接近臨界速度時(約為臨界速度74%)甚至超過本征場應變能.界面傾角增大，渡越輻射能單調非線性增大.界面與剛性基礎夾角為銳角側集中了更多的渡越輻射能.

(2)隨著載荷移動速度增大，界面附近能通量的方向性發生變化，沿界面方向傳播的能量逐漸增大.載荷移動速度接近臨界速度時界面附近能通量角密度發生極大增長.隨著界面傾斜角度增大，界面附近能通量并非單調增大，但自由場占比是單調增大的.

可以認為現行的高速鐵路路橋過渡段設置能夠在一定程度上起到減小系統動力響應的作用，但當行車速度接近基礎結構臨界速度時，不同結構之間的剛度差異將對系統動力響應起到極大的放大作用.在高速鐵路列車不斷提速的背景下，為保證行車安全性和乘客舒適性，有必要對過渡段結構設計做出優化.

本文中將高速鐵路列車簡化為一個勻速移動的點載荷，考慮列車實際載荷形式及軌道結構對載荷的分散作用，列車經過過渡段的物理模型可簡化為在一定范圍內分布的多個點載荷，以一定的時間差經過兩種介質之間的界面，多個載荷激發出的渡越輻射場也存在相應的相位差，其疊加所產生的渡越輻射場仍有待進一步研究，計算時需對多個載荷的本征場進行疊加，進而求得在多載荷條件下界面處的自由場激擾源.