隨機和區間非齊次線性哈密頓系統的比較研究及其應用1)

邱志平 姜 南

(北京航空航天大學航空科學與工程學院,北京 100191)

引言

隨著計算機技術的飛速發展,研究人員越來越追求更高效、更穩定和長時間模擬能力更強的數值算法[1].同一力學問題有牛頓力學、拉格朗日力學、哈密頓力學體系三種表示形式,其中一切可忽略耗散的物理過程都可以表示為某種哈密頓形式,但由于求解途徑不同,產生的計算結果可能是不等效的[2].傳統算法除少數例外,都不是辛算法,不可避免地帶有人為耗散性等歪曲體系特征的缺陷,用于短期模擬尚可,用于長期跟蹤則會導致結果嚴重失真[3-4].而哈密頓系統辛算法卻有保持體系結構的優點,在結構對稱性和守恒性方面優于傳統算法,特別在穩定性和長期跟蹤能力上具有獨特優越性[2-5].

哈密頓系統辛算法的思想始于20 世紀80 年代Ruth[6]和馮康[7]的工作.1983 年,Ruth[6]構造了可分哈密頓系統的前三階辛差分格式.1984 年,馮康[7]首次系統地提出了哈密頓系統的辛算法,開創了哈密頓力學數值計算的新領域.1988 年,Sanz-Serna[8]、Lasagni[9]和Suris[10]分別從不同角度給出了辛Runge-Kutta 方法的判定條件.1993 年,Sun[11]對一般的哈密頓系統構造了辛分塊Runge-Kutta 方法.2000 年前后,Bridges[12]、Reich[13]和Marsden等[14]構建了多辛算法的理論框架.之后,變分積分子、離散梯度法、投影算法、分裂組合算法、對稱算法等[15]一系列方法不斷提出并發展.近年來,無網格格式[16]、連續級Runge-Kutta 方法[17]等辛算法也相繼被提出.深入的理論分析和大量的數值實驗令人信服地表明,辛算法在數值計算中具有顯著優越性.

然而,動力系統中不可避免地存在大量的、不同程度的不確定性[18].例如,工程結構中的典型不確定性有:建模過程中的簡化操作導致所建模型存在誤差,制造環境、材料多相特征等因素使彈性模量、泊松比等材料參數具有分散性,制造及安裝誤差使結構幾何尺寸具有不確定性,測量條件、外部環境等因素使外載荷具有不確定性等[19-20].這些不確定性將引起動力響應變化,響應不確定量有時甚至能達到參數不確定量的數倍[21].此外,不確定性的存在還會使系統的性質發生改變,保守系統若存在不確定性則不再保守.根據產生機理不同,不確定性可分為隨機不確定性和認知不確定性[22-23]:隨機不確定性是由自然變異和隨機性而導致的不確定性,以隨機模型定量化;認知不確定性是指受知識水平和社會環境等因素制約而產生的認知上的不確定性,通常以區間模型定量化.因此,需要在哈密頓系統中考慮隨機和區間不確定性的影響,以確保動力學分析計算的合理有效性.

1984 年,Zambrini 首先基于變分原理提出了Nelson 隨機力學在哈密頓力學下的運動方程,逐步建立了哈密頓力學下的隨機力學體系.2002 年,Milstein 等[24]對一般的隨機哈密頓系統構造了幾類辛Runge-Kutta 方法,開創了隨機哈密頓系統辛算法這一全新的研究領域.2007 年,王麗瑾[25]提出了隨機變分積分子理論,使利用隨機生成函數構造隨機辛算法成為可能.2009 年,Bou-Rabee 和Owhadi[26]對隨機哈密頓系統構造了隨機變分積分子.近幾年,丁效華課題組[27-28]也對隨機哈密頓系統進行了研究,并構造了隨機辛Runge-Kutta、辛分塊Runge-Kutta 方法等.此外,朱位秋[29-30]研究了多自由度非線性隨機動力學系統,在國際上首次提出了隨機激勵的耗散的哈密頓系統理論,構建了非線性隨機動力學與控制的哈密頓理論框架.上述隨機哈密頓系統相關研究主要聚焦隨機白噪聲激勵,但沒有考慮系統本身的參數隨機性,并且考慮區間不確定性的哈密頓系統也未見有人研究.

哈密頓系統辛算法的工程結構應用方面,羅恩等[31]建立了多自由度系統彈性動力學的相空間非傳統哈密頓變分原理,提出了稱之為辛時間子域法的辛算法,精度和效率都具有明顯優越性.邢譽峰課題組[32-33]針對結構動力學方程構造了多種辛差分格式,得到了令人滿意的結果.高強等[34]用辛算法求解拉壓剛度不同桁架的非線性動力問題,Li 等[35]構造了一類動力學初值問題的辛算法并應用于簡諧振子和簡支梁,Yang 等[36]用辛算法對超長細桿進行動力學數值模擬.也有學者對多辛算法的工程結構應用開展了相關研究,如梁[37]、板[38]、桿[39]的動力響應等.然而,用哈密頓系統求解含不確定性的結構動力響應還少有人研究.

本文針對隨機和區間不確定性,對含參數不確定性的非齊次線性哈密頓系統的動力響應分析進行首次嘗試,提出兩種不確定性哈密頓系統的參數攝動法,突破傳統哈密頓系統只適用于保守系統的局限性,并開展兩種哈密頓系統不確定性響應的相容性研究,以期為結構動力響應評估提供更加有效穩定的數值計算方法.

1 確定性非齊次線性哈密頓系統

考慮哈密頓正則方程

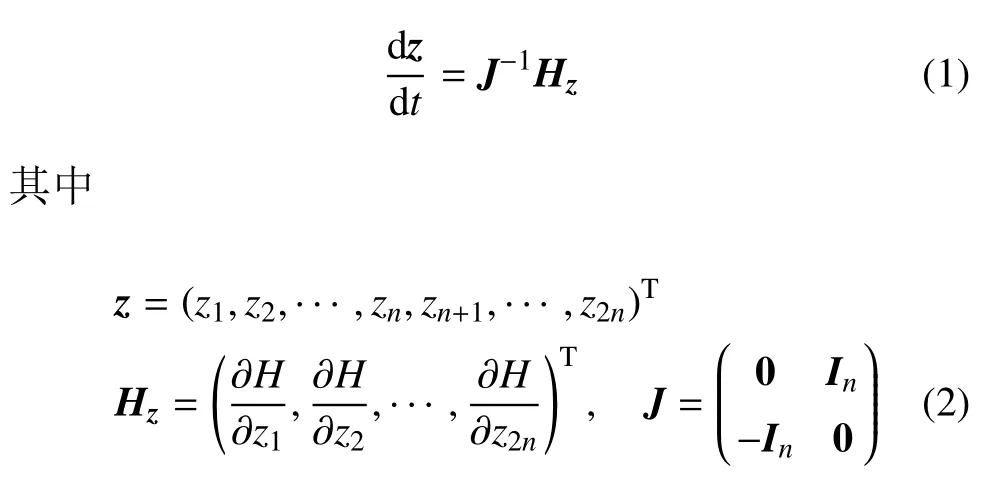
其中,In是n階單位矩陣;J是標準單位辛矩陣,滿足J?1=JT=?J;H稱為該系統的哈密頓函數.

哈密頓系統(1)稱為線性的,如果哈密頓函數H是z的二次型

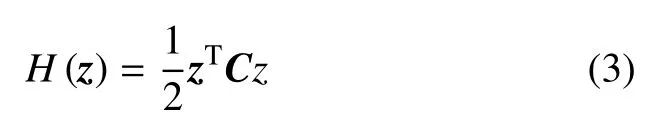
其中C為對稱矩陣,即CT=C,于是正則方程(1)能夠表示為

其中B=J?1C是無窮小辛陣,即滿足JB+BTJ=0.

非齊次線性哈密頓系統是在線性哈密頓系統基礎上增加了非齊次項

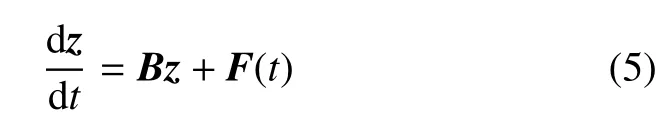
其中F(t)是與時間t有關的向量.

此時,哈密頓函數H′可以表示為

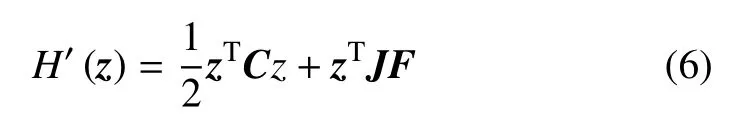
從而,非齊次線性哈密頓系統(5)可以表示為哈密頓正則方程(1)的形式.

對于哈密頓系統,其相空間配備著一個標準辛結構,也就是一個閉的微分2 形式

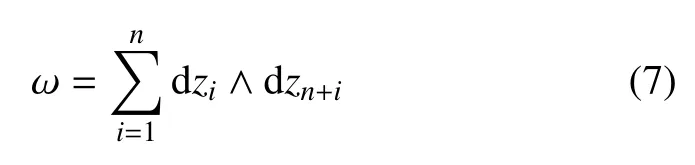
哈密頓系統相流保持相空間的辛結構不變,即

2 含擾動非齊次線性哈密頓系統的參數攝動法

假設非齊次線性哈密頓系統(5)中的矩陣B和向量F(t)中元素與系統參數b=(b1,b2,···,bm)T有關,此時,哈密頓系統(5)可以寫為

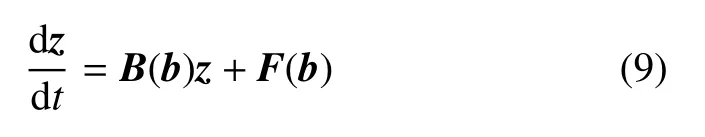
當系統參數b=(b1,b2,···,bm)T存在擾動時,矩陣B(b)和向量F(b)由標稱值變化到擾動系統,分析擾動對哈密頓系統響應z的影響.

根據攝動理論,引入小參數ε、參數b、矩陣B、向量F和哈密頓系統的解z可以分別寫為攝動級數展開形式

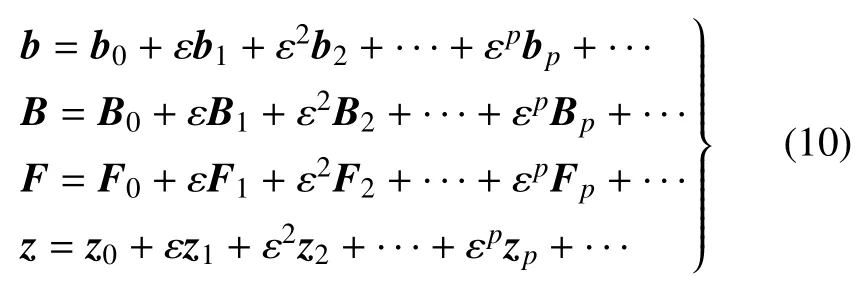
其中,ε 是小于單位1 的小量,b0,B0,F0和z0分別是b,B,F和z的標稱值,bi,Bi,Fi和zi(i=1,2,···,p)分別是其第i階攝動量.含ε 的項表示其與標稱值相比是一個很小的量,在這種情況下,哈密頓系統的解z只有小變化.通過選擇使|ε| 足夠小的參數可以使級數收斂.

將式(10)代入式(9),得

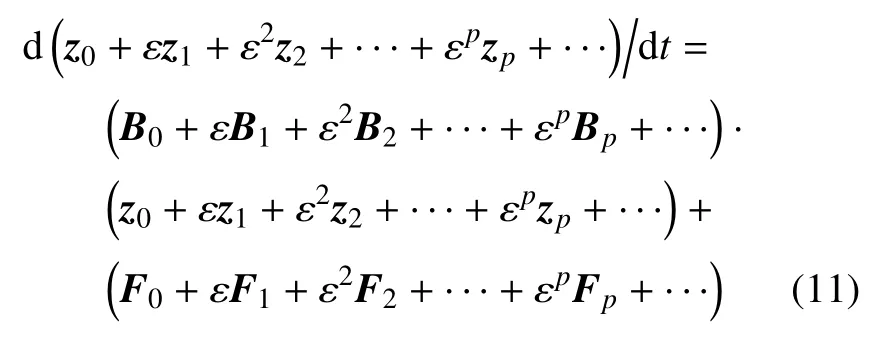
將式(11)展開,比較ε 的同次冪系數,可得

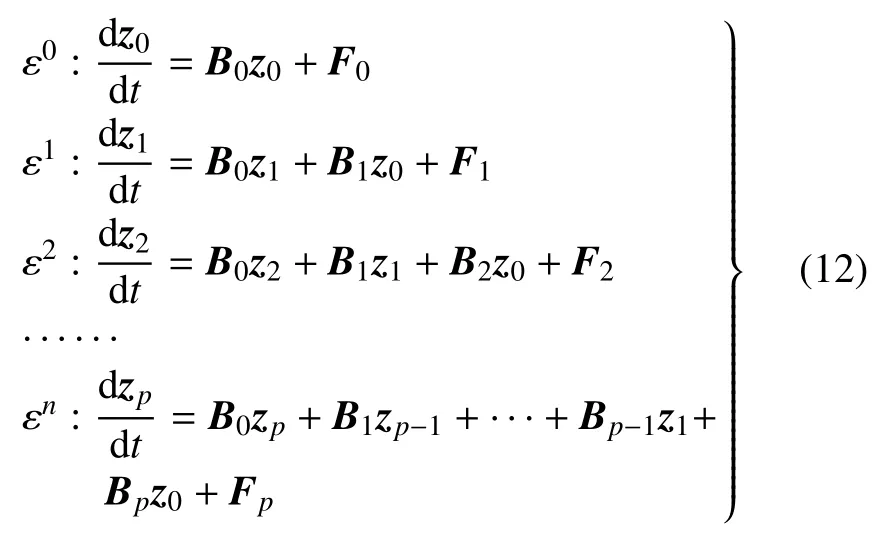
運用辛算法求解式(12)中第1 式可以得到z的標稱部分,即z0.本文中采用的辛算法均為歐拉中點格式.對式(12)中其他式子的Bi和Fi(i=1,2,···,p),可以通過Taylor 展開獲得,即將B和F在b=b0處分別進行Taylor 展開,得到

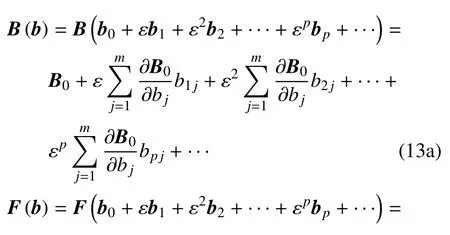
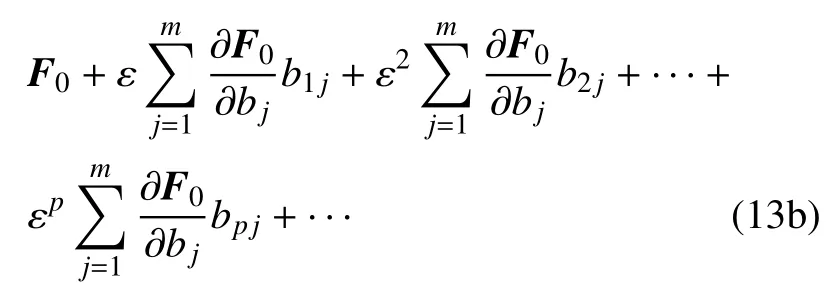
其中bij(i=1,2,···,p;j=1,2,···,m)是bi的分量.

由式(10)和式(13),可知

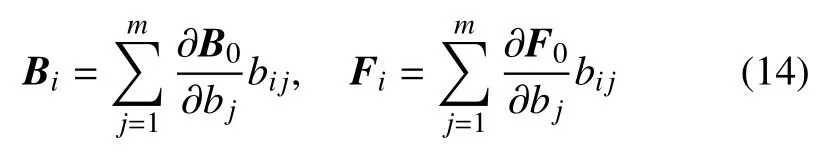
將式(12)中第1 式求得的z0和式(14)求得的B1,F1代入式(12)中第2 式并利用辛算法求解,可以求得z的第1 階攝動量z1;進而可以通過依次求解式(12)中其他式子得到zi(i=2,3,···,p)的值.從而,z就可以按式(10)求得.在每一步都采用辛算法求解保證計算結果能夠保持體系結構特征,避免傳統算法帶有的人為耗散性等歪曲體系特征的缺陷.在實際計算中,為了方便求解,常常展開到第1 階攝動.

當參數b存在的擾動為隨機或區間不確定性時,上述參數攝動法可以推廣至求解隨機或區間非齊次線性哈密頓系統,詳細求解過程如下面第3、4 節所述.

3 隨機非齊次線性哈密頓系統的參數攝動法

當系統參數b=(b1,b2,···,bm)T是隨機變量時,矩陣B、向量F和哈密頓系統的解z也是隨機的,它們可以分別看作圍繞確定性部分(均值)有一個隨機小擾動.因此,基于前述攝動理論,同樣引入小參數ε,將b,B,F和z分別表示為

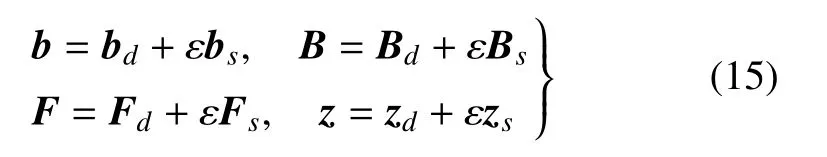
其中,bd,Bd,Fd和zd分別是b,B,F和z的確定性部分;bs,Bs,Fs和zs分別是其隨機部分,且它們的均值均為0.

將式(15)代入式(9),得

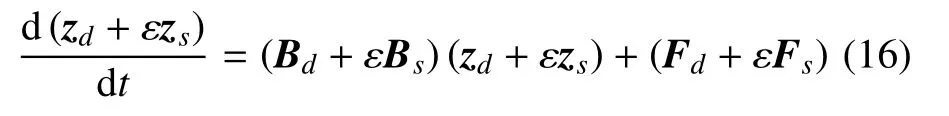
將式(16)展開,忽略O(ε2)高階項,并比較ε 的同次冪系數,可得

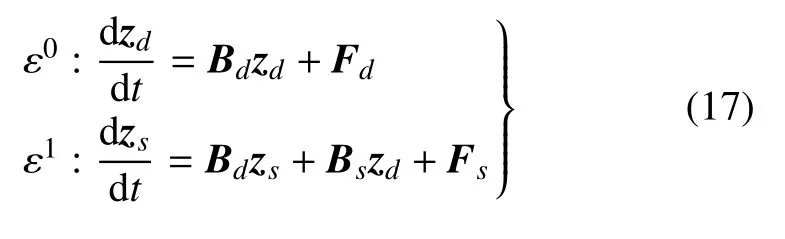
利用辛算法求解式(17)中第1 式可以求得z的確定性部分zd,即為z的均值.但無法由式(17)直接確定z的隨機部分zs,需要進行變換后加以求解.

對式(15)求取數學期望,有

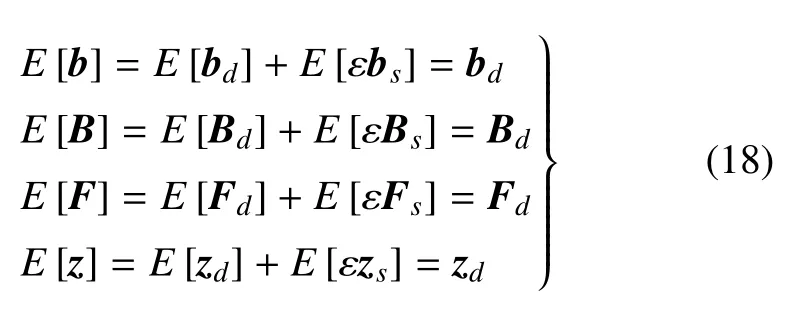
由于zd是一個確定性的向量,所以zd與z,zd與zs均相互獨立,從而可得

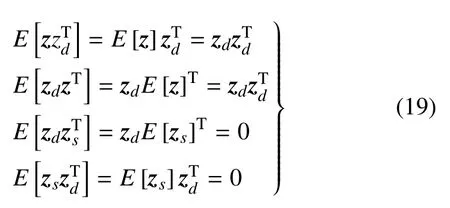
因此,z的協方差矩陣可以寫為

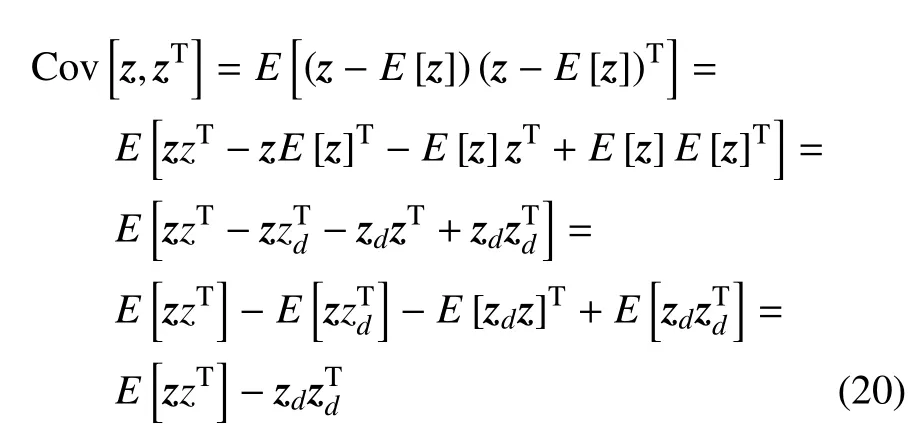
式(20)中的E[zzT]可以寫為

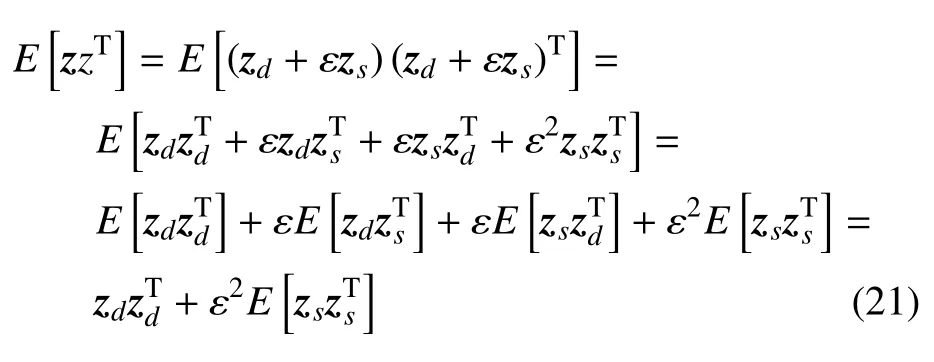
將式(21)代入式(20),可得協方差矩陣為

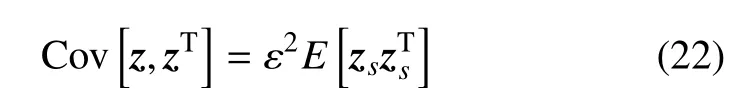
該協方差矩陣的對角元素表示各點的方差,其他非對角元素表示各點間的協方差.因此,z的各分量zi(i=1,2,···,2n)的方差為

同理,b的各分量bj(j=1,2,···,m)的方差為

將z在z=zd處進行一階Taylor 展開得到

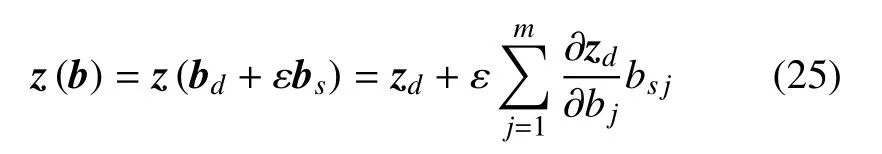
其中,bsj(j=1,2,···,m)是bs的分量.

從而,z的隨機部分zs可以表示為

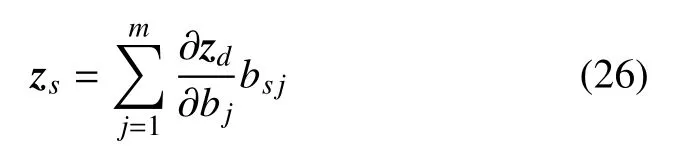
同理,Bs和Fs可以表示為

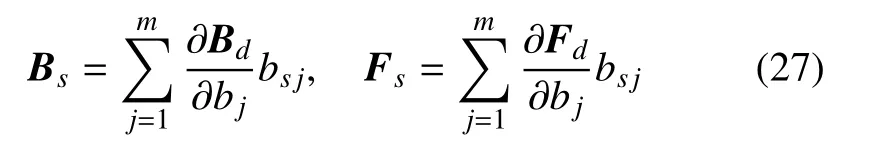
將式(26)～式(27)代入式(17)中第2 式,得

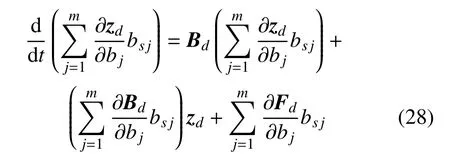
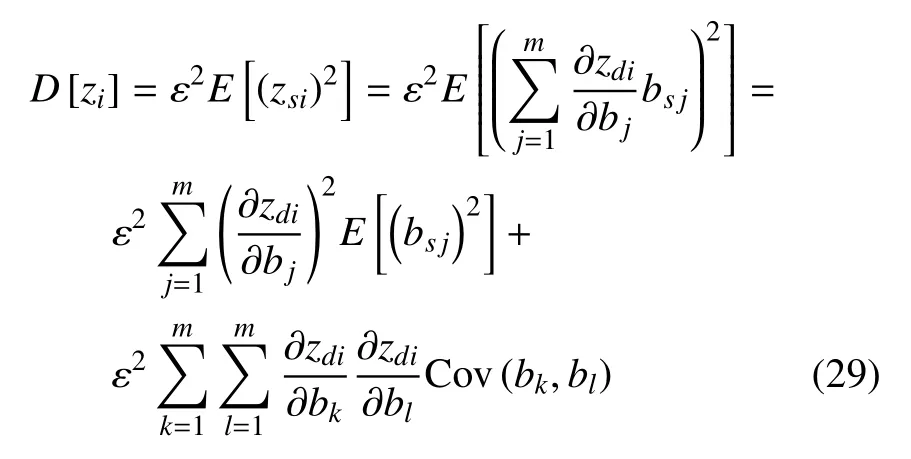
其中Cov(bk,bl)表示bk和bl的協方差.

若參數bj是相互獨立的,Cov(bk,bl)為0,則式(29)可以簡化為

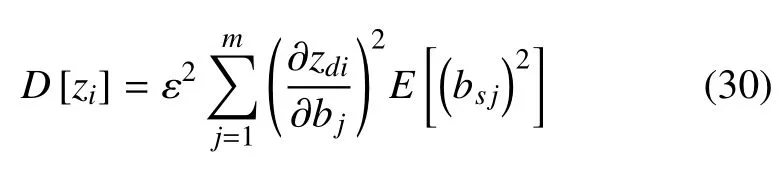
將式(24)代入式(30),就可以得到z的各分量zi(i=1,2,···,2n)的方差

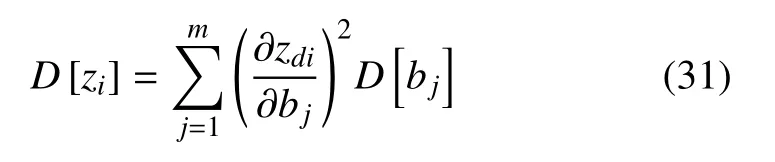
因此,zi(i=1,2,···,2n)的標準差為

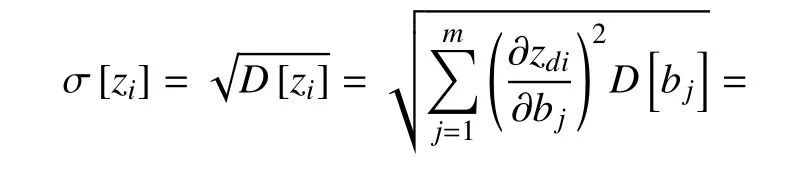
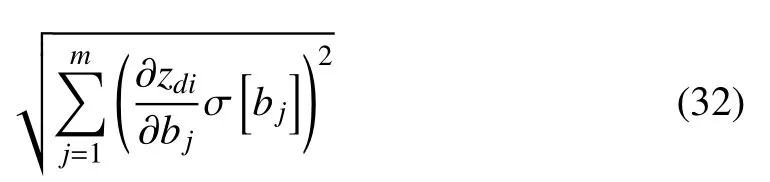
其中σ[bj]是bj(j=1,2,···,m)的標準差.

在計算求解過程中,求解式(17)中第1 式求得z的均值zd和求解式(28)求得z的隨機部分zs都采用了辛算法,確保計算結果能夠保持體系結構特征.

令k為正整數,則對zi(i=1,2,···,2n)而言,距其均值的距離為k倍標準差的范圍為

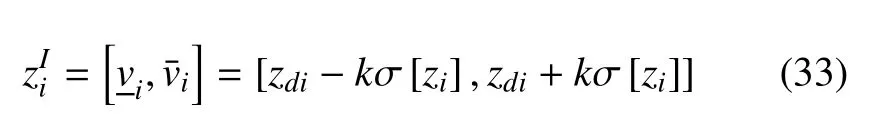
其中范圍的上界和下界分別為

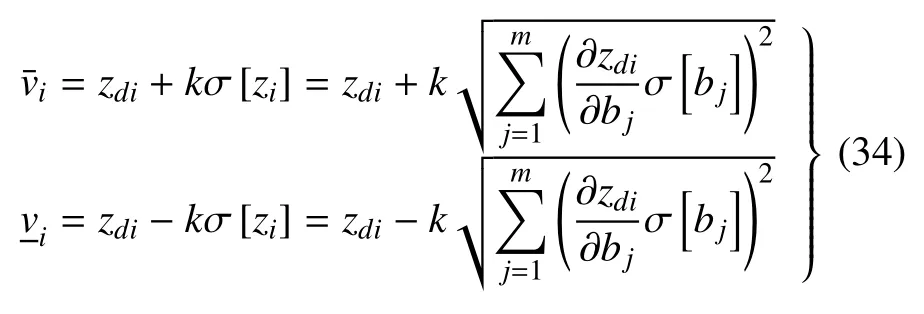
4 區間非齊次線性哈密頓系統的參數攝動法

當系統參數b=(b1,b2,···,bm)T是區間變量時,即參數b在一個區間向量內取值,矩陣B、向量F和哈密頓系統的解z也分別在一個區間范圍內取值

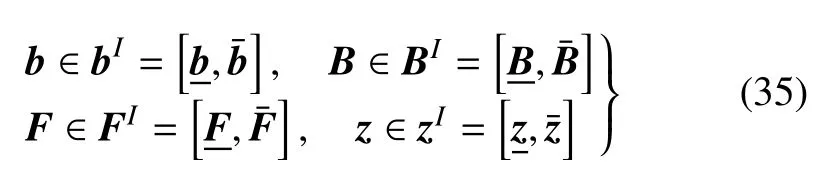
其中,bI,FI和zI是區間向量,BI是區間矩陣,分別是分別是其上界.

此時,哈密頓方程(9)可寫為

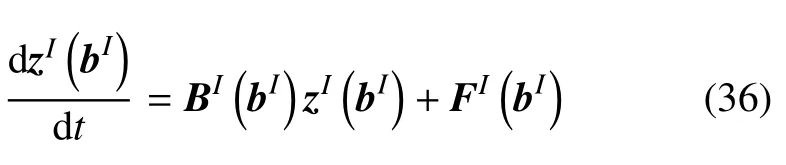
式(36)是區間非齊次線性哈密頓方程.

bI,BI,FI和zI的中值和半徑分別為

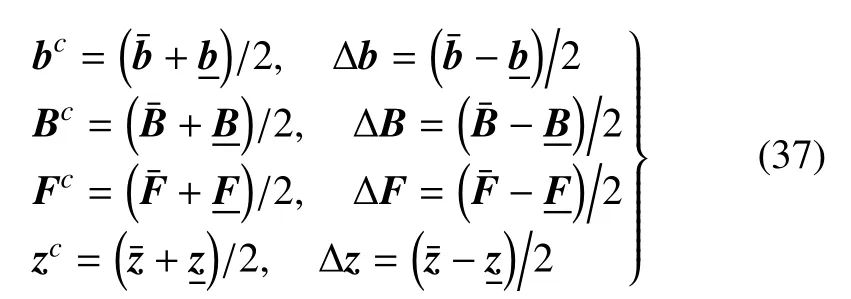
利用區間中心表示法,bI,BI,FI和zI可以分別表示為

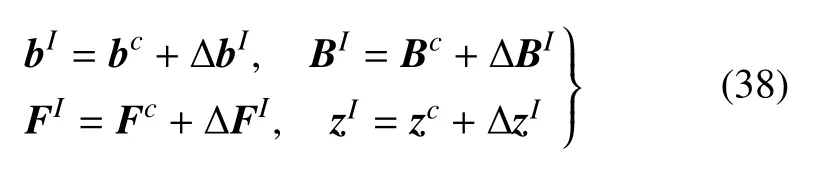
其中

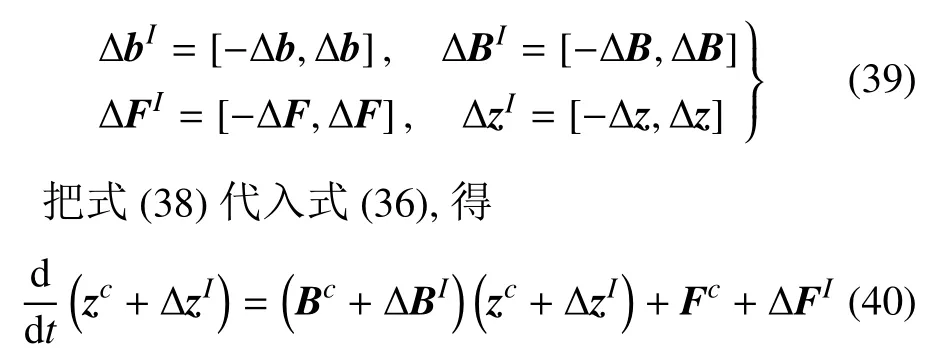
如果將?bI,?BI,?FI和?zI分別看作圍繞bc,Bc,Fc和zc的擾動,則可以采用第2 節所述參數攝動法求解區間哈密頓方程(40).

按照區間的含義,引入小參數ε,式(40)可以表示為:由于參數b存在小擾動δb,導致B,F和z產生小擾動δB,δF和δz,且滿足

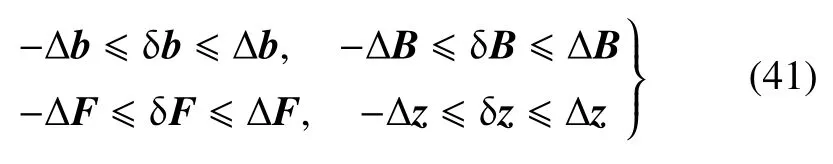
條件下的擾動方程的形式

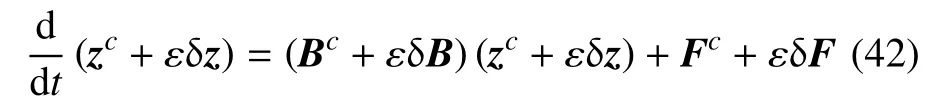
式(41)和式(42)所表示的問題可以理解為:在參數中值bc已知,從而能夠確定中值Bc和Fc,而小擾動δb的具體取值未知但其取值范圍(41)已知,小擾動δB和δF的具體取值也未知但其取值范圍(41)可以確定的情況下,確定哈密頓系統的解z的界限.展開式(42)并比較ε 的同次冪系數,可得

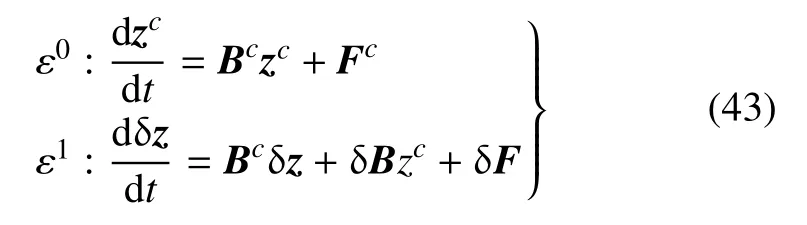
運用辛算法求解式(43)中第1 式可以求得z的中值zc.由區間擴張,式(43)中第2 式可寫為

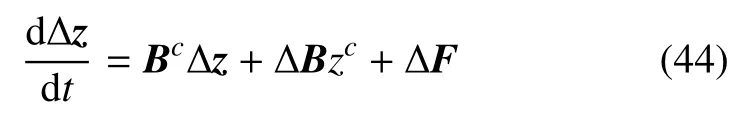
將z在z=zc處進行一階Taylor 展開得到

其中,δbj(j=1,2,···,m)是δb的分量.

從而可得δz的表達式

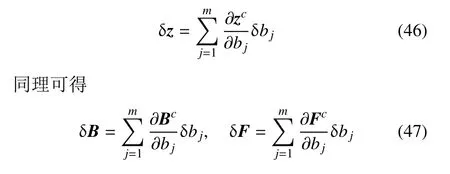
式(46)和式(47)的區間擴張形式為

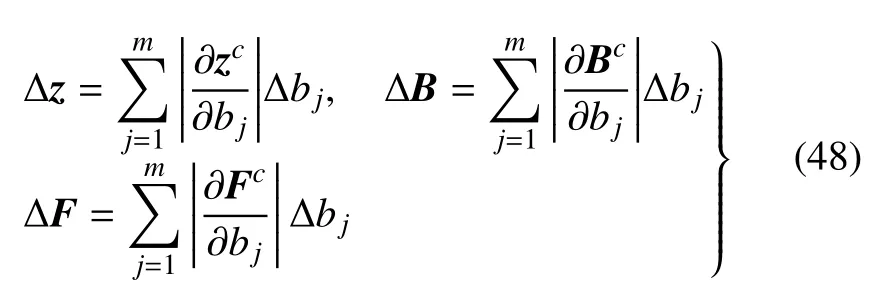
其中,?bj(j=1,2,···,m)是?b的分量.

將式(48)代入式(44),得

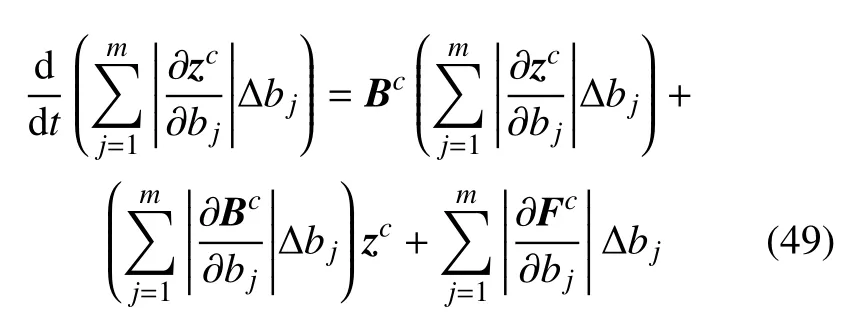
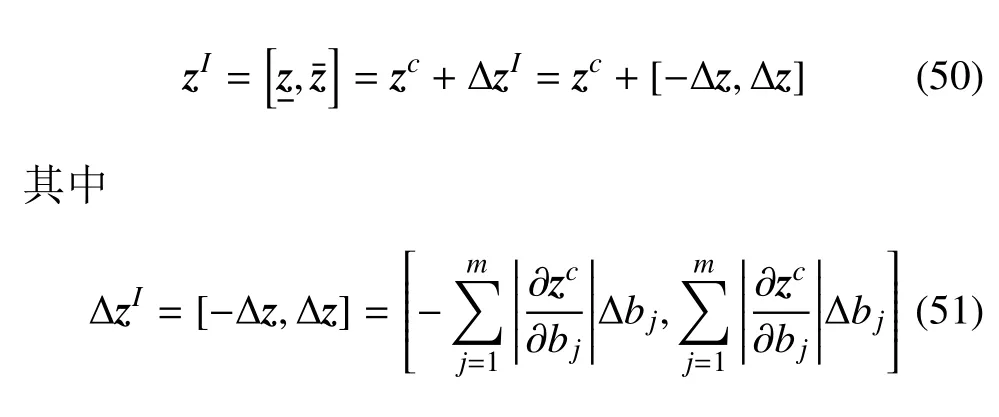
在計算求解過程中,求解式(43)中第1 式求得z的中值zc和求解式(49)求得z的半徑?z都采用了辛算法,同樣確保計算結果能夠保持體系結構特征.

由區間相等的定義可得z的上界和下界分別為

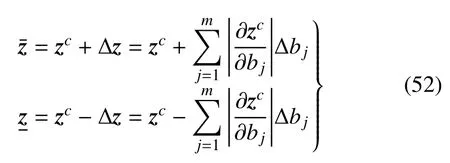
z的分量形式zi(i=1,2,···,2n)的上界和下界分別為

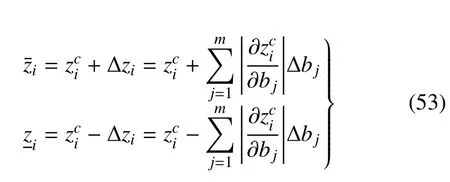
5 隨機和區間非齊次線性哈密頓系統比較

不確定性是客觀存在的,無論是隨機方法還是區間方法,只是描述不確定性的不同形式,不能從本質上改變不確定性對響應的影響規律,利用兩種方法得到的不確定性響應理應具有相容性.因此,本節對隨機和區間非齊次線性哈密頓系統的分析結果進行比較,探究兩者響應界限的包含關系.

假定參數b的區間范圍由概率統計信息獲取,即可以表示為距其均值距離為k倍標準差的形式

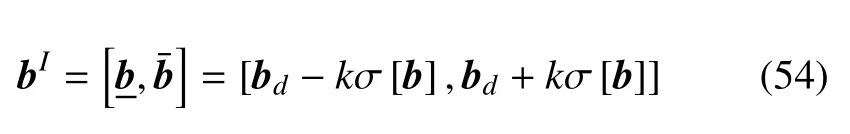
其中,k為正整數,σ[b]是b的標準差,b的上界和下界分別為

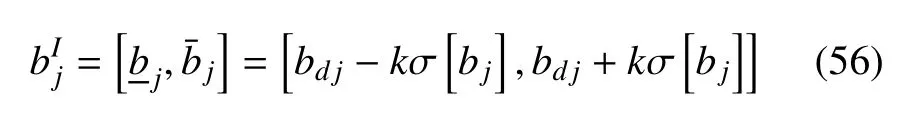
由式(54)～式(55),可以得到參數b的區間中值和半徑與隨機確定性部分和標準差之間存在關系

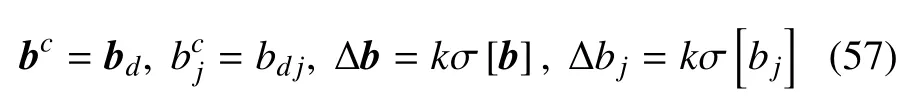
哈密頓系統的解z的區間中值與隨機確定性部分同樣存在關系

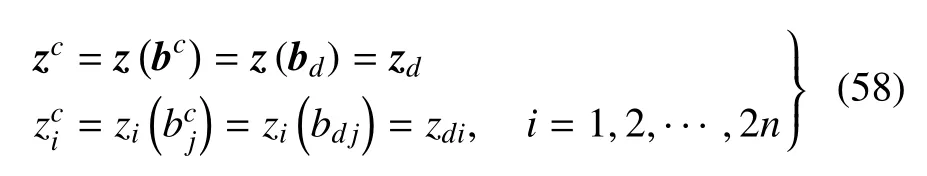
將式(57)的分量形式代入式(53),得到zi(i=1,2,···,2n)的上界和下界

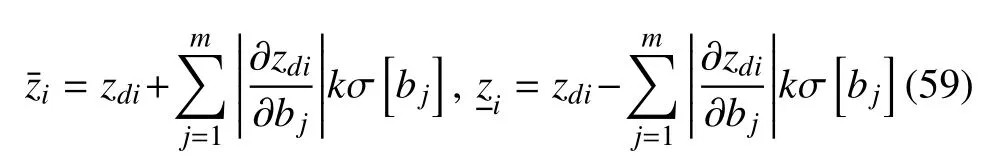
對于參數bj,切比雪夫不等式成立

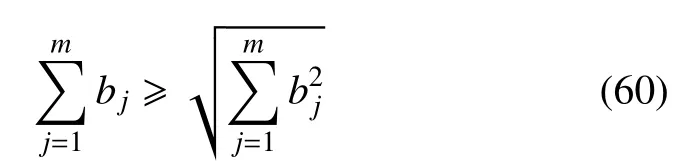
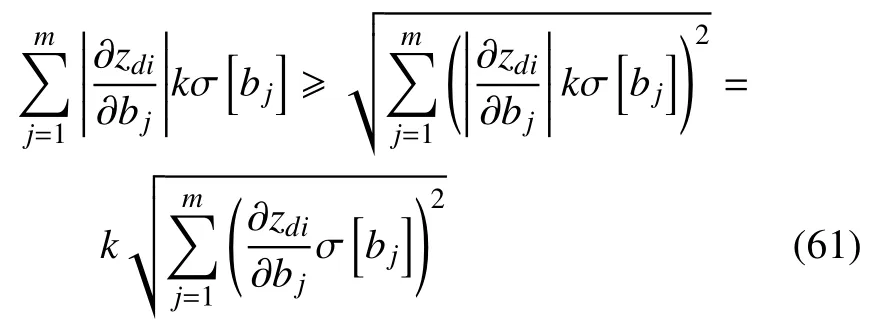
由不等式(61),可以得到由隨機方法確定的上下界(34)和由區間方法確定的上下界(59)存在關系

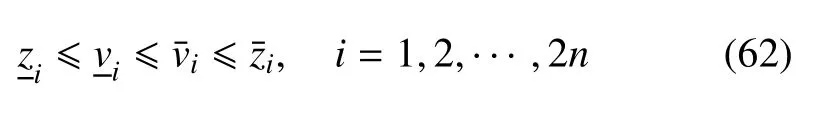
式(62)表示,在由概率統計信息確定不確定性參數的區間范圍的情況下,對于不確定性非齊次線性哈密頓系統,由區間方法獲得的哈密頓系統的解的范圍比由隨機方法獲得的范圍大,即區間方法得到的上界比隨機方法得到的上界大,而區間方法得到的下界比隨機方法得到的下界小.

6 數值算例

為了驗證所提方法在結構動力響應中的可行性和有效性,本節給出兩個數值算例,包括懸臂梁和復合材料層合板,并將本文所提隨機、區間方法(分別簡記為SHPM、IHPM)計算結果與傳統隨機、區間方法(分別簡記為TSM、TIM)計算結果相比較.

6.1 懸臂梁

考慮如圖1 所示11 節點、10 單元懸臂梁在正弦激勵作用下的動力響應.梁長L=1 m,橫截面積A=2 cm2,橫截面的慣性矩Iz=2 cm4,材料泊松比ν=0.3.正弦激勵P(t)=?psin(1600πt)N 作用在節點3 的豎直方向,初始條件為˙x(0)=0,x(0)=0.

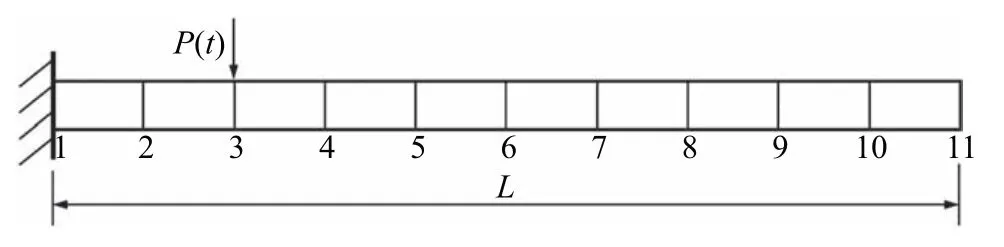
圖1 11 節點、10 單元懸臂梁Fig.1 A cantilever beam with 11 nodes,10 elements

由于材料中不可避免的分散性及測量誤差,材料的彈性模量、密度和正弦激勵幅值均具有不確定性,假設它們所在的區間范圍I如表1 所示;同時假設它們在區間范圍內服從正態分布,均值μ 和標準差σ 也如表1 所示.

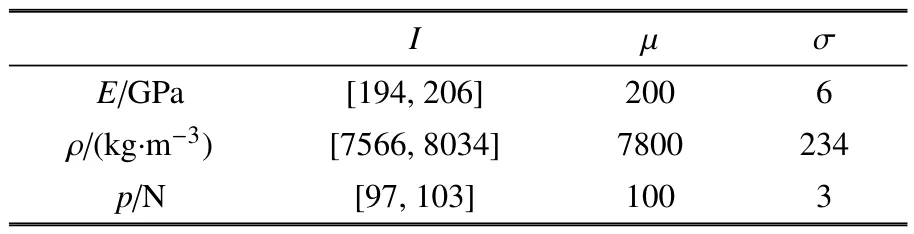
表1 材料彈性模量、密度和正弦激勵幅值的不確定性Table 1 Uncertainties of elastic modulus,density of the material and the amplitude of the harmonic excitation

懸臂梁整體運動微分方程為

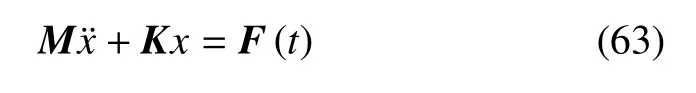
其中,M是懸臂梁整體質量矩陣,與材料密度ρ 有關;K是整體剛度矩陣,與材料彈性模量E有關;F(t)是整體載荷向量,與正弦激勵P(t)有關.

令y=則整體運動方程(63)可以表示為

首先考察在時間步長?t=40μs 下利用辛算法求解哈密頓系統(64)和直接求解方程(63)方法計算節點11 的響應標稱值.利用辛算法求解哈密頓系統(64)計算得到的t=0～0.1 s 內的響應標稱值曲線如圖2(a)所示,整體呈周期性變化,但直接求解方程(63)得到的響應標稱值很短時間內即發散,如圖2(b)所示,只有當時間步長足夠小,如?t=2μs 時,直接求解方程(63)才能得到和利用辛算法求解哈密頓系統(64)相同的結果.這一穩定性差異反映了哈密頓系統辛算法能夠保持體系結構特征,體現出利用哈密頓系統辛算法求解微分方程的優越性.

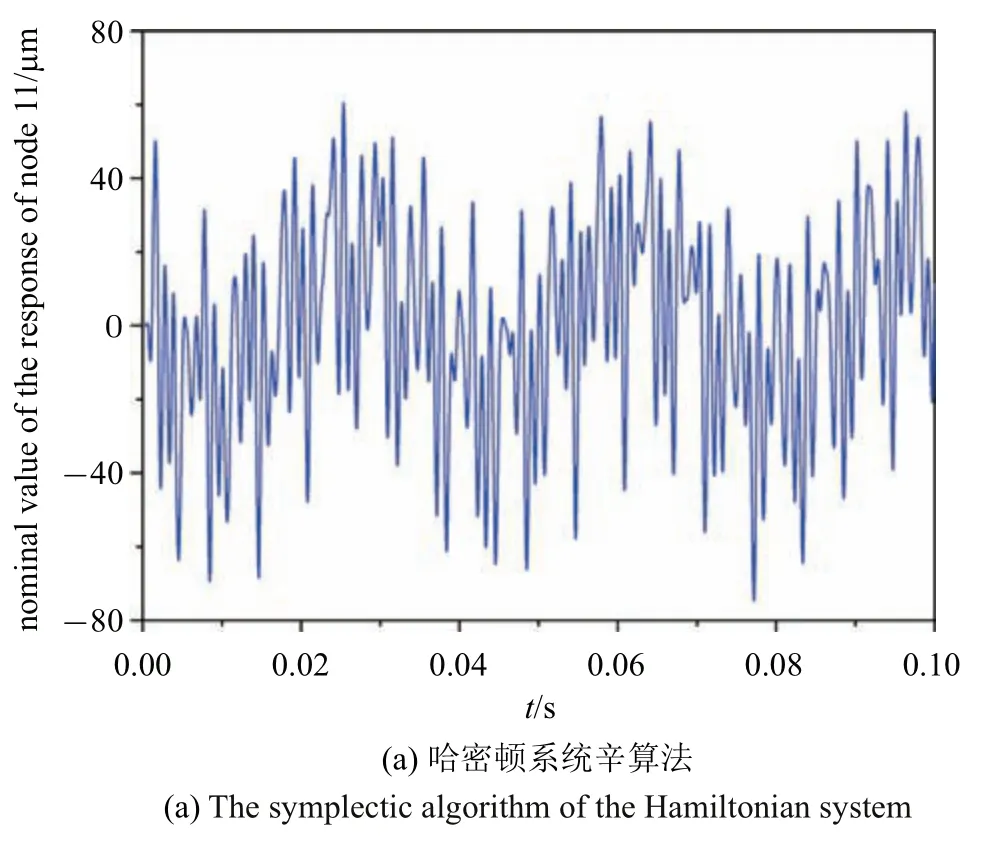
圖2 時間步長?t=40μs 下利用不同算法計算得到的節點11 的響應標稱值Fig.2 The nominal value of the response of node 11 obtained by different algorithms with time step ?t=40μs

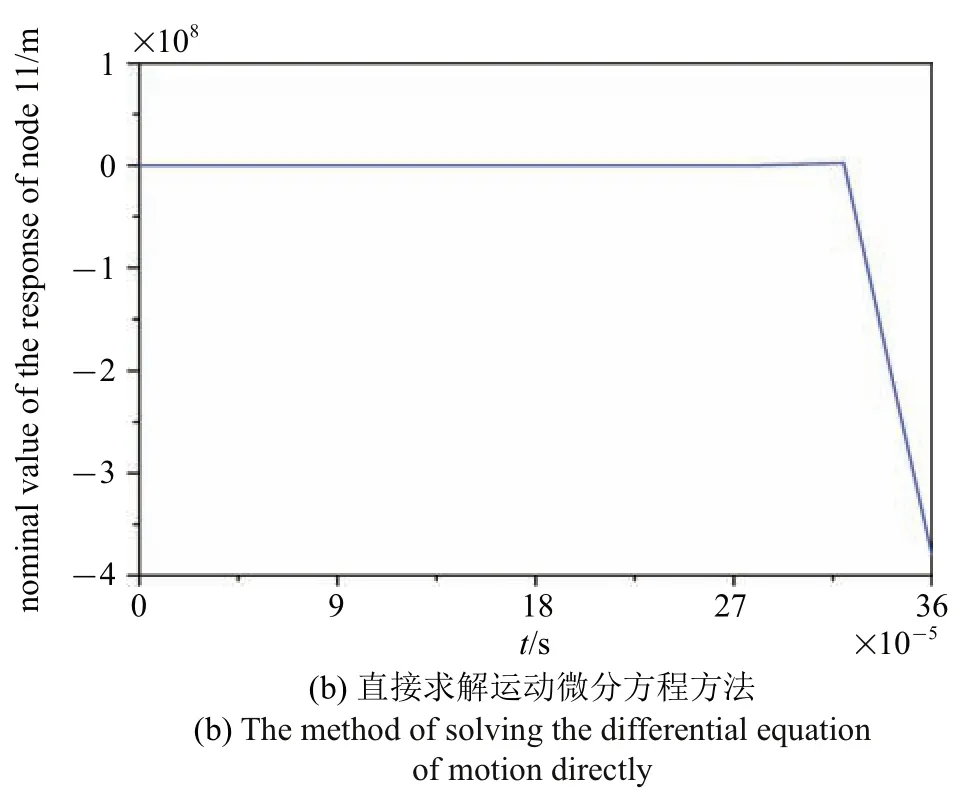
圖2 時間步長?t=40μs 下利用不同算法計算得到的節點11 的響應標稱值(續)Fig.2 The nominal value of the response of node 11 obtained by different algorithms with time step ?t=40μs(continued)

圖3 本文所提方法和傳統方法計算得到的節點11 的響應曲線Fig.3 The response curve of node 11 obtained by SHPM,IHPM,TSM and TIM

在同一時間步長?t=2 μs 下本文所提隨機、區間非齊次線性哈密頓系統的參數攝動法和傳統隨機、區間方法計算得到的節點11 在t=0～5.0 ms 內的響應曲線如圖3 所示,其中圖3(a)～圖3(b)分別為兩種隨機、區間方法得到的響應曲線,圖3(c)為本文所提隨機、區間方法計算得到的響應曲線,響應標稱值也繪制于圖3 中.本文所提隨機、區間方法和傳統隨機、區間方法計算得到的節點11 在t=3.5 ms 時刻的位移上下界如表2 所示.

表2 本文所提隨機、區間方法和傳統隨機、區間方法計算得到的節點11 在t=3.5 ms 時刻的位移上下界Table 2 The upper and lower bounds on the displacement of node 11 at t=3.5 ms obtained by SHPM,IHPM TSM and TIM

由圖3 和表2 可知,本文所提隨機、區間方法得到的響應上下界曲線分別與傳統隨機、區間方法所得響應上下界曲線均幾乎完全重合,結果非常相近,驗證了所提隨機、區間方法的準確性和有效性.此外,本文所提區間方法得到的響應區間范圍包含本文所提隨機方法得到的響應區間范圍,即區間方法所得響應上界大于隨機方法所得響應上界,而區間方法下界小于隨機方法下界,這一現象與前述理論推導相符.

前述內容驗證了在較大時間步長?t=40μs 下哈密頓系統辛算法相較于直接求解運動微分方程方法計算響應標稱值的有效性和優越性,也驗證了在較小時間步長?t=2μs 下本文所提隨機、區間方法所得響應區間范圍的準確性.為了進一步檢驗本文所提隨機、區間方法在較大時間步長下所得響應區間范圍也能保持較高精度,下面將本文所提隨機、區間方法在時間步長?t=40μs 下得到的響應區間范圍與蒙特卡洛模擬方法(簡記為MCM)得到的響應區間范圍進行比較.其中,蒙特卡洛模擬在較小時間步長?t=2μs 下進行,樣本點數目設置為1.0×105,對于每一樣本點都采用辛算法求解,從而可將蒙特卡洛模擬結果視為精確值.本文所提隨機、區間方法和蒙特卡洛模擬方法計算得到的節點11 在t=0～5.0 ms 內的響應曲線如圖4 所示.

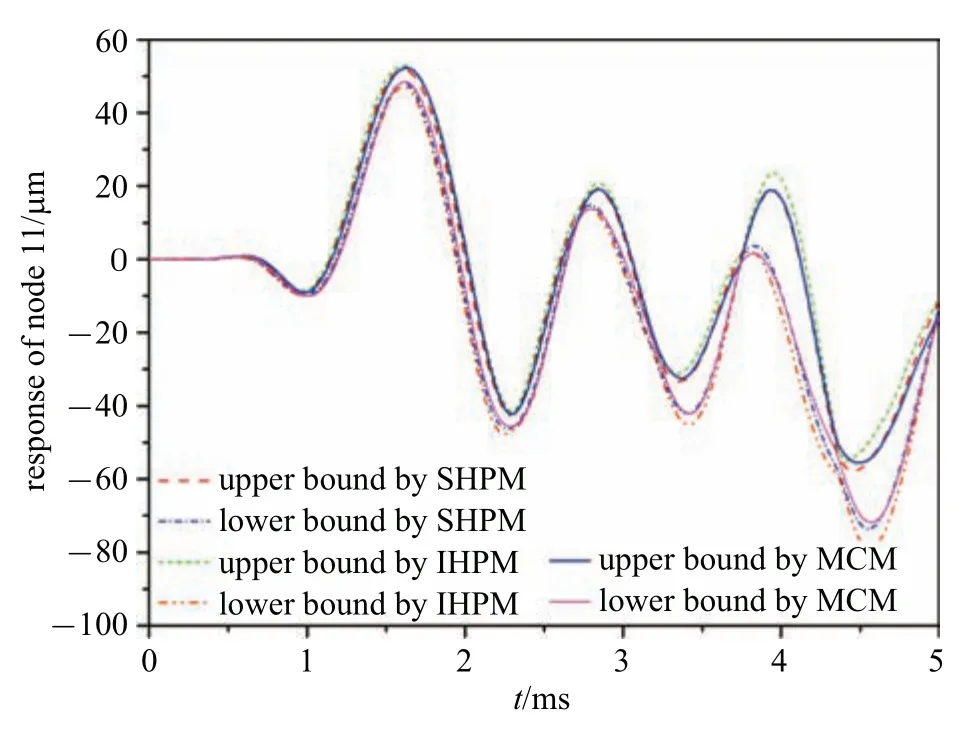
圖4 本文所提隨機、區間方法和蒙特卡洛模擬方法計算得到的節點11 的響應曲線Fig.4 The response curve of node 11 obtained by SHPM,IHPM and MCM

由圖4 所示,本文所提隨機方法與蒙特卡洛模擬方法得到的響應上下界曲線差別微小,盡管由于較大時間步長原因導致精度有一定下降,但仍得到了較為滿意的結果.這一現象體現出本文所提方法在較大時間步長下也能得到具有較高精度的結果,再次驗證了本文所提方法的優勢.而對于本文所提區間方法,由于區間擴張效應,得到的響應區間范圍包含本文所提隨機方法和蒙特卡洛模擬方法得到的響應區間范圍,與前述理論推導相一致.

6.2 復合材料層合板

考慮如圖5 所示的邊長為L=1.0 的四邊固支的復合材料層合板結構,其由5 層正交各向異性材料鋪設而成,鋪設角度為(0?,90?,0?,90?,0?),每層厚度為t=0.012,質量密度ρ=1.0.板中心處受一垂直于板的正弦激勵作用P(t)=?psin(200πτ),初始條件為(0)=0,x(0)=0.材料屬性和正弦激勵幅值同樣均具有不確定性,假設其區間范圍I如表3 所示;同時假設它們在區間上服從正態分布,均值μ和標準差σ也如表3 所示.采用4 結點矩形薄板單元,將板劃分為相等的16 個單元.為方便,所有數據均采用無量綱量.

圖5 四邊固支復合材料層合板Fig.5 A composite laminate with fully clamped boundary conditions

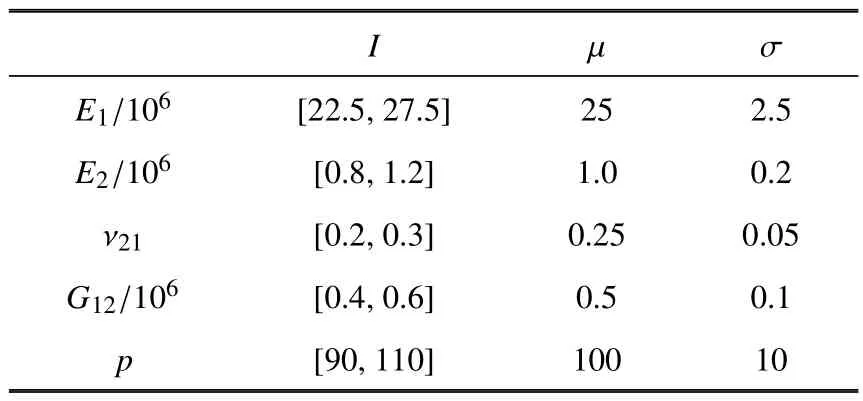
表3 材料屬性和正弦激勵幅值的不確定性Table 3 Uncertainties of material properties and the amplitude of the harmonic excitation

考慮板中心處z方向的動力響應.在同一時間步長?τ=1.0×10?5下,本文所提隨機、區間方法和傳統隨機、區間方法在τ=0～0.05 內計算得到的響應范圍以及響應標稱值曲線如圖6 所示,其中圖6(a)～圖6(b)分別為兩種隨機、區間方法得到的響應曲線,圖6(c)為本文所提隨機、區間方法計算得到的響應曲線.本文所提隨機、區間方法和傳統隨機、區間方法計算得到的τ=0.025 時刻位移上下界如表4 所示.

由圖6 和表4 可知,本文所提隨機、區間方法得到的響應上下界曲線分別與傳統隨機、區間方法所得響應上下界曲線同樣近乎完全重合,再次驗證了所提方法的有效性.同時,本文所提區間方法得到的響應上界比隨機方法得到的響應上界大,區間方法得到的響應下界比隨機方法得到的響應下界小,也與理論推導和算例6.1 現象一致.

圖6 本文所提方法和傳統方法計算得到的板中心處z 方向的響應曲線Fig.6 The response curve of the center of the plate in z-direction obtained by SHPM,IHPM,TSM and TIM

下面進一步比較在時間步長?τ=2.5×10?4下利用哈密頓系統辛算法和直接求解運動微分方程計算得到的響應標稱值,曲線分別如圖7(a)～圖7(b)所示.由圖7 可知,利用哈密頓系統辛算法求解能夠得到滿意的響應標稱值,然而在該時間步長下直接求解運動微分方程得到的響應標稱值同樣在很短時間內發散.這一現象再次體現了哈密頓系統辛算法由于能夠保持體系結構特征而具有很好的穩定性,凸顯了哈密頓系統辛算法在數值模擬中的顯著優越性.

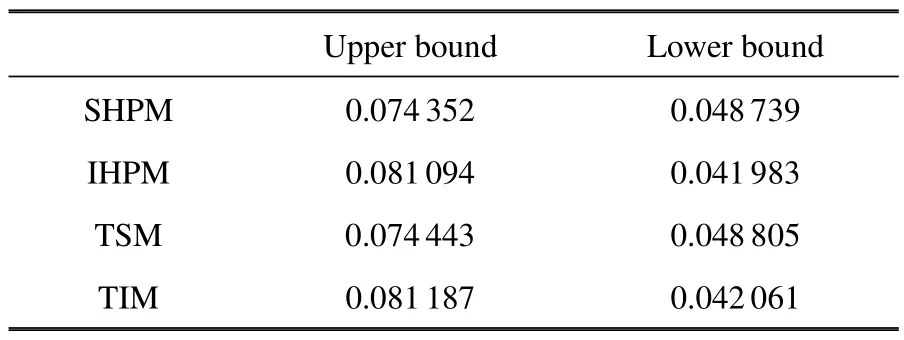
表4 本文所提隨機、區間方法和傳統隨機、區間方法計算得到的板中心處z 方向在τ=0.025 時刻的位移上下界Table 4 The upper and lower bounds on the displacement of the center of the plate in z-direction at τ=0.025 obtained by SHPM,IHPM TSM and TIM

圖7 時間步長?τ=2.5×10?4 下利用不同算法計算得到的板中心處z 方向的響應標稱值Fig.7 The nominal value of the response of the center of the plate in z-direction obtained by different algorithms with time step ?τ=2.5×10?4

7 結論

本文考慮非齊次線性哈密頓系統,基于攝動理論發展了含小參數擾動的哈密頓系統的參數攝動法,以此為基礎分別將小擾動看作隨機、區間擾動,提出了分別針對隨機、區間不確定性哈密頓系統的參數攝動法,突破了傳統哈密頓系統的限制,并由切比雪夫不等式證明了兩者響應分析結果的相容性關系,通過兩個綜合考慮外載荷和不確定性的結構動力響應數值算例驗證得到了如下結論:

(1)在同一較大時間步長下,由直接求解運動微分方程的方法得到的響應標稱值很可能會發散,而將運動微分方程引入到哈密頓系統后再利用辛算法計算仍然可以得到令人滿意的結果,體現了哈密頓系統辛算法具有很好的穩定性,保持體系結構特征的優勢明顯,在數值仿真模擬方面的顯著優越性;

(2)在同一較小時間步長下,本文所提隨機不確定性哈密頓系統的參數攝動法得到的響應上下界分別與傳統隨機方法所得響應上下界結果近乎完全一致,差別微小,本文所提區間方法得到的響應上下界也分別與傳統區間方法所得響應上下界極為相近,驗證了所提方法的有效性;

(3)本文所提隨機方法在較大時間步長下得到的響應上下界與蒙特卡洛模擬方法在較小時間步長下得到的響應上下界基本吻合,說明本文所提方法在較大時間步長下也能得到具有較高精度的結果,再次驗證了本文所提方法的優越性;

(4)當參數的區間范圍由概率統計信息確定,即區間半徑表示為距其均值距離為標準差的整數倍時,本文所提區間方法計算得到的響應區間范圍包含本文所提隨機方法計算得到的響應區間范圍,即區間響應上界大于隨機響應上界、區間響應下界小于隨機響應下界.