基于線性回歸新模型的插補方法實證研究

曾梅

摘? 要：在實際生活中搜集數據時，數據缺失的情況是很常見的。在通常的情況下，當輔助變量和缺失變量之間有著較強的線性關系時，如果我們利用回歸插補方法對缺失數據進行插補是合理的。在很多研究中，對于回歸插補法一般是使用最小二乘法，在本文中將根據研究者提出來的一種新線性回歸估計方法，運用到回歸插補中，并和普通最小二乘回歸插補及均值插補進行比較，運用R語言進行數據缺失的模擬分析，最后得出前者所得效果更好，豐富了缺失數據插補方法，并且為實際運用中選取處理缺失數據的插補方法時，提供了較多的選擇范圍。

關鍵詞：缺失數據? 回歸插補? 均值插補? R語言

中圖分類號：O212.1? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ? 文章編號：1674-098X（2020）10（c）-0094-07

Abstract： When collecting data in real life， there are often missing data. Under normal circumstances， when there is a strong linear relationship between the auxiliary variable and the missing variable， we use the regression imputation method to impute the missing data is very effective. In many studies， the least squares method is generally used for regression interpolation. This article will apply a new linear regression estimation method proposed by the researcher to the interpolation method of missing data， and use ordinary least squares regression Imputation and mean imputation are compared， and the R language is used to simulate and analyze the missing data. Finally， it is concluded that the former has better results， which provides more options for selecting missing data imputation methods in actual applications.

Key Words： Missing data; Regression imputation; Mean imputation; R language

在現在這個信息時代，對數據的處理變得越來越為重要。對于許多數據都會存在缺失的情況，例如在UCI數據集中，含有大量的缺失數據，缺失比例超過了40%;在我們運用統計年鑒上的數據時，也會發現對于一些指標的數據，在有些年份有，而有些年份卻沒有;在醫療數據的搜集中也會發現由于病人的離世或者提前放棄了治療從而導致數據存在缺失的情況。直接刪除法是處理缺失數據最簡單的方法，但是采取這種方法會導致大量的信息丟失，造成分析結果的不準確，不能充分滿足數據分析的要求，而統計學方法對數據的完整性具有很高的要求，因此對缺失數據的插補在數據的初步清洗中扮演著重要的角色。Little和Rubin從缺失機制將缺失數據劃分為完全隨機缺失（MCAR），隨機缺失（MAR）和非隨機缺失（MNAR）[12]。為了方便，本文選取完全隨機缺失機制進行研究。

在實際生活中，我們會發現，有很多數據之間都具有一定的聯系，但是經常會出現數據丟失的情況，因此回歸插補法具有重大的研究意義。最小二乘回歸是人們較為熟悉的方法，由于其簡單方便，因此在使用回歸插補時，常用最小二乘來進行估計。為了尋找其他有效的方法，本文將基于一種新的回歸方法進行插補，并和最小二乘進行比較，期望得到更加有效的回歸插補方法。

本文的基本脈絡如下：第1部分介紹回歸插補和均值插補的基本原理;第2部分介紹最小二乘回歸法以及學者提出來的新的線性回歸模型;第3部分運用實際數據進行實證研究，驗證新方法的有效性;第4部分對文章進行總結分析。

1? 回歸插補和均值插補介紹

1.1 回歸插補

對于實際中的很多數據，都存在一定的線性關系。顧名思義，回歸插補的主要思想就是根據各變量之間的關系建立回歸模型，然后把缺失變量看成因變量，運用建立的模型得到預測值，并把其作為缺失值的填補值。

回歸插補的步驟如下：

第一步：對于給定數據集，檢測出變量之間如果具有很強的相關性，則可以運用回歸插補。

第二步：利用完整數據集建立回歸模型，把缺失變量看成因變量，把與缺失變量對應的輔助變量代入得到的回歸模型中，得到的值作為對應缺失值的代替值。

回歸插補法是一種單一插補方法，主要針對數據集中存在一個變量缺失的情況，也即是單變量缺失的模式。利用回歸插補法時，由于其操作簡單，在建立回歸模型時通常使用最小二乘。

1.2 均值插補

均值插補是運用現有數據的均值來代替缺失值的一種方法。均值插補主要包括單一均值插補和分層均值插補，均值插補已近常被廣泛的使用。本文主要使用的是單一均值插補，因此僅簡單介紹單一均值插補方法。

單一均值插補是利用已觀測到的變量并計算其均值作為該缺失變量的填補值。其插補值可以表示為：

其中示性函數，為變量中已經觀測到的個數。

因此，可以得到總體的均值估計為：

進一步計算插補后的樣本方差，可以得到：

2? 線性回歸方法的介紹

2.1 最小二乘回歸（OLS）

2.1.1 一元線性回歸

最小二乘回歸是非常有效的方法，由于它的簡單性，在經濟、醫療等領域都具有廣泛的應用。最小二乘法的主要思想是使得預測值和實際值差的平方和最小，然后對相應的參數進行估計。一元線性回歸的數學模型如下：

通過最小二乘可以得到和的參數估計如下：

在上式中，表示截距，表示斜率，表示自變量，表示因變量，和表示均值。

2.1.2 多元線性回歸

在現實生活中，影響因變量的因素通常有很多，因此出現了多元線性回歸，它也是對一元線性回歸的推廣。模型如下（3）式：

2.2 線性回歸新模型

最小二乘法發展成熟，且計算簡單被運用廣泛運用在各個領域。但是其在預測方面并不是最準確的，而且對異常值也較為敏感，因此趙茂先和余陽提出了在某些情況下預測精度和絕對誤差的效果比最小二乘好的估計方法[1]。

為了方便，把第一種方法作為記為ML1，其主要的思想是把已知數據的均值和所有數據的斜率求平均作為線性回歸模型的斜率，同時再根據均值和斜率求出截距，公式如下：

同樣的道理，把第二種方法作為記為ML2，由于自變量和因變量都滿足方程

在上式中，和未知，和已知，因此和可以得到：

根據（6）式可以解得和的估計值

這是ML2方法的一元形式，推廣到多元的形式可以得到多元線性函數的參數估計如下所示：

其中

3? 模擬分析

我們將利用實際的數據，運用最小二乘回歸的插補方法、均值插補法以及ML1插補、ML2插補對具有不同缺失率的數據進行填補，通過對不同評價指標比較，得出ML1插補和ML2插補的有效性。

3.1 評價指標

3.1.1 從插補值的角度

（1）平均絕對誤差。

其中表示變量中缺失值的個數，表示缺失的插補值，表示實際值。

（2）均方誤差。

從插補值的角度出發，本文用MAE、MSE來判定插補效果的好壞。平均絕對誤差表示的是填補值和真實值之間差值的平均，MAE越小，說明填補值和真實值之間的誤差越小，說明填補效果越好，反之，說明效果越差。對于均方誤差MSE也是同樣的道理。

3.1.2 從模型的角度

（1）調整后的決定系數。

其中SSE表示殘差平方和，SST表示總的離差平方和。

（2）回歸系數相對誤差。

其中表示原始數據得到的回歸系數，表示進行行插補之后再進行回歸得到的與之對應系數，對應的回歸系數相對誤差越小越好。

3.2 數據說明

本文采用的數據集1是全國各地區2018年的人均消費支出和人均可支配收入的數據，把前者看成因變量，后者作為自變量。數據來源于中國統計年鑒。數據集2是R語言里自帶的iris數據集，把Petal.Length看成因變量，Petal.Width作為自變量，對于這兩個數據集采用一元線性回歸的模型進行填補。對于多元線性回歸的模型，使用的是影響我國財政收入的數據，均來源于《中國統計年鑒》。其中財政收入為因變量，稅收，年末從業人員數為自變量。分別設置因變量的缺失情況為為完全隨機缺失，且缺失率為5%、10%、20%、30%。

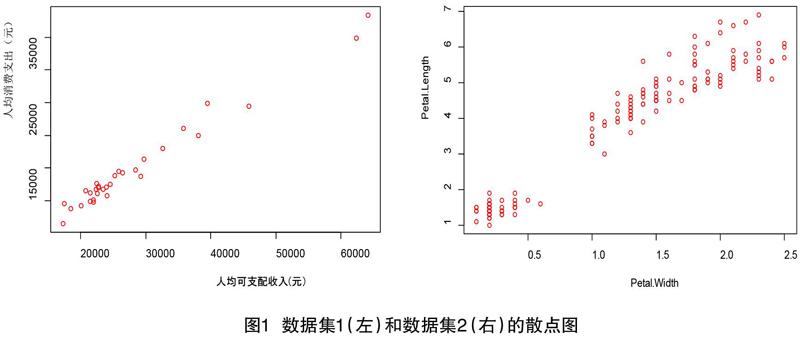
為了探究各地區人均消費支出和人均可支配收入的數據關系，做出散點圖如圖1所示。

從圖中我們可以看到數據集1中的人均消費支出和人均可支配收入呈線性關系，同時計算兩者的相關系數為0.9881。數據集二中兩個變量之間也具有很強的線性關系，且通過計算得到相關系數為0.9639。因此對于兩個數據集來說，如果數據有缺失的情況，運用回歸插補處理是可行的。

3.3 結果分析

3.3.1 數據集一的結果分析

對于數據集1，采用完全隨機缺失的模式進行模擬研究。設置因變量的缺失率依次為5%，10%，20%，30%，運用均值插補、最小二乘回歸插補，ML1插補，ML2插補四種方法得到的MAE、MSE結果如表1。

從平均相對誤差來看，比較四種方法可以發現，對于數據不同的缺失率情況下，ML1的MAE值最小，其次是最小二乘和ML2，最大的是均值插補的方法。從均方誤差來看，不同的缺失率下，ML1的MSE值最小，其次是最小二乘和ML2，最大的是均值插補的方法。所以評價指標無論是MAE還是MSE，ML1的插補效果最好，其次是最小二乘和ML2，均值插補的效果最差。為了更加直觀的看出各種方法的插補效果，做出不同方法的MAE和MSE的對比圖，如圖2所示。

從模型角度比較來看，分析不同方法不同缺失率下線性回歸得到的調整。

原始數據的為0.9756，從調整的來看，在不同的缺失率之間，運用最小二乘、ML1、ML2所得到的相差不大，但是均值插補后進行回歸得到的和原始數據的相差較大。運用各種插補方法之后得到完整的數據集，再對數據進行線性回歸，得到回歸系數和原始數據的回歸系數的相對誤差情況如表3。

從表3可知，當缺失率為5%時，和的MAE最小的是ML1方法，其次是最小二乘和ML2的方法，最大的是均值插補的方法。當缺失率為10%，20%，30%時，得到結果和缺失率為5%時一致。

從平均相對誤差來看，比較四種方法可以發現，對于數據不同的缺失率情況下，ML2的MAE值最小，其次是最小二乘和ML1，最大的是均值插補的方法。從均方誤差來看，不同的缺失率下，ML2的MSE值最小，其次是最小二乘和ML1，最大的是均值插補的方法。所以評價指標無論是MAE還是MSE，ML2的效果最好，其次是最小二乘和ML1，均值插補的效果最差。為了更加直觀的看出各種方法的插補效果，做出不同方法的平均相對誤差對比圖和均方誤差對比圖，如圖3所示。

如表4、表5，從模型角度比較來看，分析不同方法不同缺失率下線性回歸得到的調整對于iris數據來說，原始數據的為0.9266，在缺失率不同時使用不同的方法ML2的結果和最小二乘的結果相差不大，均值插補得到的和原始數據相差較大。運用各種插補方法之后得到完整的數據集，再對數據進行線性回歸，得到回歸系數和原始數據的回歸系數的相對誤差情況如表6。

從表6可得，當缺失率為5%時，比較和的相對誤差最小的是ML2方法，其次是最小二乘和ML1的方法，相對誤差最大的是均值插補的方法。當缺失率為10%，20%，30%時，得到和缺失率為5%時同樣的結果。

3.3.2 數據集3的結果分析

對于多元線性回歸，使用的數據集是影響我國財政收入的數據，均來源于《中國統計年鑒》。其中財政收入為因變量，稅收，年末從業人員數為自變量。同樣設置因變量的缺失機制為完全隨機缺失，缺失率分別為5%，10%，20%，30%。運用最小二乘和ML2兩種方法進行多元線性回歸插補得到MAE、MSE結果如表7。

從表中我們可以看出，當缺失率為5%時，ML2的方法得到的平均相對誤差，均方誤差都比最小二乘的方法要小，說明相比于最小二乘，此時運用ML2的方法效果較好。當因變量的缺失率為10%，20%時，ML2方法所得到的MAE大于使用最小二乘的MAE，但是ML2 方法所得到的MSE遠遠小于使用最小二乘所得到的MSE。

4? 結語

缺失數據的情況是非常常見的，這在進行數據分析時給我們帶來很大的困難，如果只是單純的刪掉那些具有缺失數據的變量，這會使得我們丟掉很多現有的信息，使得分析的結果不準確。同時由于一些統計分析方法通常對數據的完整性要求較高，因此對缺失數據進行插補之后再進行相關的統計分析是非常有必要的。

文中針對具有較強相關性的數據，設置的缺失模式為完全隨機缺失，對數據進行模擬驗證分析，采用最小二乘回歸插補，ML1回歸插補、ML2回歸插補、均值回歸插補四種方法進行分析，從插補值的角度和模型的角度進行對比，最終發現，運用均值插補的效果最差，而且均值插補會隨著數據缺失率的增加，而削弱插補的效果。而ML1回歸插補、ML2回歸插補在某些情況下優于最小二乘回歸插補，因此可以運用到處理關聯性數據進行插補，為實際運用中插補方法提供了更多的選擇。

參考文獻

[1] 趙茂先，余陽.一種線性回歸新模型[J].統計與決策，2019，35（18）：21-25.

[2] 廖祥超.九種常用缺失值插補方法的比較[D].昆明：云南師范大學，2017.

[3] 董世杰.三種線性回歸多重插補法的模擬比較[D].天津：天津財經大學，2017.

[4] 程豪.大數據背景下缺失數據問題及對策[J].中國統計，2019（10）：72-74.

[5] 魏娜，孫霞.統計缺失數據處理方法的比較研究[J].知識經濟，2017（18）：29-30.

[6] 鄧建新，單路寶，賀德強，等.缺失數據的處理方法及其發展趨勢[J].統計與決策，2019，35（23）：28-34.

[7] 馮麗紅.調查數據缺失值常用插補方法比較的實證分析[D].石家莊：河北經貿大學，2014.

[8] 張海霞.城鎮居民醫療費用影響因素的調查中對不同機制下應答偏倚并存時的校正[D].太原：山西醫科大學，2015.

[9] 邱貽濤，吳劉倉，馬婷.缺失數據下聯合均值與方差模型的參數估計[J].數理統計與管理，2015，34（4）：621-627.

[10] 呂丹.一類數據挖掘算法及其在宮頸癌智能診斷中的應用[D].長春：長春工業大學，2019.

[12] 張曉琴，程譽瑩.基于隨機森林模型的成分數據缺失值填補法[J].應用概率統計，2017，33（1）：102-110.

[13] 桂風云，魏傳華.地理加權似乎不相關回歸模型及其估計[J].統計與決策，2016（8）：4-6.

[14] 吳劉倉，張家茂，邱貽濤.缺失偏態數據下線性回歸模型的統計推斷[J].統計與信息論壇，2013，28（9）：22-26.

[15] 安佰玲，王森，胡洪勝.線性回歸模型在因變量缺失下的約束估計[J].統計與決策，2013（11）：19-21.

[16] 楊徐佳，于倩倩，王森.因變量缺失下線性回歸模型的估計與檢驗[J].淮北師范大學學報：自然科學版，2011，32（1）：24-28.

[17]劉寶慧.缺失數據情形下的回歸插補及其方差分析[J].甘肅聯合大學學報：自然科學版，2009，23（1）：19-21.

[18]袁中萸. 多元線性回歸模型中缺失數據填補方法的效果比較[D].長沙：中南大學，2008.