天線方向系數的一類計算逼近方法

劉俊群

(南京電子技術研究所,南京 210039)

天線的方向系數是天線的核心性能指標之一,準確計算方向系數是高性能天線應用的核心要求.本文基于平面近場測試理論、實測數據和快速傅里葉變換算法,系統闡述基于近場測試來數值計算天線方向系數的原理,并進行深入的誤差分析.本文選擇一種方向圖函數和方向系數已知的被測天線,來檢驗所討論的誤差評估方案.評估分兩步實現,第一步,針對這一天線,采用標準的近場測試配置,仿真模擬出(相當于實際測量出)一套平面近場數據.第二步,基于這套近場數據,利用數值積分計算出天線方向系數.本文使用或提出了四種數值算法,分析了提出的后三種算法本身的誤差來源,并開發出程序搜索方案,確定出后兩種算法的最小誤差界.隨后,利用這四種數值算法分別得出天線的方向系數.結果表明,計算所得的近場方向系數都比真實方向系數大,但誤差不超過0.6 dB.這一結果對實際應用中正確評估基于近場測試的天線方向系數準確性有重要參考價值.

1 引 言

天線是實現電磁波輻射與接收的基本設備,廣泛應用于廣播、通信、雷達、導航等應用系統中.一支好的天線,首先要能夠高效率輻射和接收電磁波,即輸入天線的電磁場功率能夠大部分被輻射出去或接收回來.其次,要根據實際需求,實現方向性.簡單來說,方向性是指天線輻射或接收的電磁波功率密度跟空間方向緊密相關:某些方向電磁波功率密度很大,而某些方向電磁波功率密度很小直至忽略不計.典型如跟蹤雷達天線,它的電磁波功率只聚焦于空間很狹窄的方向區域,以實現辨別和測定特定目標位置.電磁波天線已經用于國家經濟活動的不同層面和千家萬戶.這一事實表明,無論是從應用物理研究角度還是適應實際發展需求角度,高效天線設計與制造不會是一個過時的課題.

天線輻射的電磁場空間方向分布特性是天線的主要性能,天線的方向系數是性能核心指標之一.雖然天線的形式多種多樣,但物理上,任一天線的輻射性能可通過天線的歸一化方向圖函數F(θ,φ)來描述.天線在空間球坐標 (θ,φ)方向的方向系數D(θ,φ)定義為該方向輻射強度與整個空間所有方向的平均輻射強度之比.方向系數因此可理解為天線聚集電磁波能量程度大小的度量.天線方向系數 D(θ,φ)與歸一化方向圖函數 F(θ,φ)的關系如下[1]:

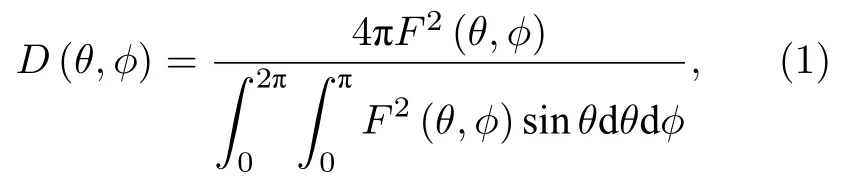
(1)式是計算任意天線方向系數的基本公式.工程計算中,通常所說的天線方向系數是指 D(θ,φ)的最大值 D0.根據 (1)式,D0公式為

如上所述,方向系數D0是一支天線最重要的性能指標之一,其準確可靠計算是天線設計與應用需要關注的核心問題之一.天線另一個重要性能指標“增益”G(θ,φ)與方向系數 D(θ,φ)緊密相關,本文著重于方向系數的計算,對天線增益不做進一步討論,在功率損耗可忽略的情況下,天線方向系數與天線增益大小相同.

根據(2)式,計算方向系數必須首先獲得天線歸一化方向圖函數 F(θ,φ)的值,但是除了幾種幾何形狀簡單的天線外,實際上很難獲得 F(θ,φ)的解析表達式.工程上,通過實際天線的平面近場測試數據來計算 F(θ,φ)是一種可行方法,基于天線平面近場測試數據實現F(θ,φ)和D0的高精度計算成為電磁場計算的一個重要課題.

天線平面近場測試已形成一套比較成熟的理論[2],其中探頭在天線輻射方向端測試采樣的所有點構成一個橫向、縱向間距均勻的矩形柵格平面,該平面與被測天線相距一般為2λ—10λ,這里λ為被測電磁波波長,獲得數據為探頭在測試采樣點感應到的復電壓或復電流,該數據與被測天線激發的電磁場成正比.顯然,平面近場測試獲得數據為一個復數矩陣,矩陣大小由測試選擇的橫向、縱向采樣點數決定.

平面近場測試理論是一個有一定誤差的工程理論,這里列舉平面近場測試的主要誤差源:第一,天線遠場與平面波譜的簡單正比關系式是平面近場波數譜積分利用駐相法獲得的近似計算結果;第二,平面近場離散采樣帶來的高波數譜貢獻被省略的誤差;第三,平面近場有限大小測試平面導致的截斷誤差;第四,一般近場測試數據處理未考慮探頭方向性帶來的誤差.當然,也可從電磁場等效原理來分析平面近場測試技術的誤差源.另外,平面近場測試只考慮被測天線靠近探頭側即主要輻射方向半空間的電磁場分布,實際天線一般滿足此條件,背瓣方向電磁場相對較弱,在計算時一般不予考慮,認為天線偏離探頭側的背面半空間電磁場為零.

如上所述,盡管平面近場測試理論和技術有一定誤差,但是實際工作中仍然被廣泛使用,實踐證明平面近場測試誤差在根據被測天線特點選擇對應的測試條件后可以容忍直至忽略不計.因此,基于天線平面近場測試數據實現F(θ,φ)和D0的高精度計算仍具有重要的工程意義.

實際應用中,一般是在獲得了被測天線近場復數矩陣數據后,通過近場-遠場快速傅里葉變換(fast Fourier transform,FFT) 快速算法[3]來計算天線的歸一化方向圖函數 F(θ,φ),再由 (2)式結合數值積分算法來計算天線的方向系數D0,從而形成一整套完備的天線性能數據,特別是較為準確可靠的方向系數D0的值,以用于雷達等實際探測應用.這就引出了本文要關注的關鍵問題:根據(2)式,結合數值積分算法獲得的方向系數準確可靠嗎? 與被測天線真實方向系數比較有多大誤差?分析這種誤差并給出評估結論,成為本文主要的研究內容之一.

事實上,本文作者所在單位已經有專業科技人員開發出數值計算程序—處理近場 (processing near field,PNF),以計算、處理平面近場測試獲得的被測天線近場數據,包括計算被測天線方向系數D0.這一PNF程序在本單位被廣泛使用于各種天線的平面近場測試數據分析與處理,經過實踐驗證,算法本身具有公認的基本準確度,其優點是計算速度很快,但是本文作者對其算法的具體細節未能獲知,其嚴格準確度需要通過測試數據計算進行評估.

本文作者也曾利用美國矩陣實驗室(Matrix Laboratory,MATLAB)軟件開發了相關程序計算D0值.結果顯示,針對不同的近場幅相分布數據,與PNF對比,兩者計算所得的D0結果在大多數情況下存在一定偏離.本文的仿真算例中表1—表7給出了共7個算例的結果比對,其中方法1)乃PNF程序計算方法,而方法2)—4)乃本文將要敘述的方法.鑒于此,迫切需要對天線方向系數的算法進行全面分析評估,以求既準確又快速地逼近天線的真實方向系數D0.平面近場測試環境下的被測天線本身具有真實的方向系數(真值D0),但是由于平面近場測試方法具有一定誤差,根據該方法獲得的測試數據矩陣計算獲得的方向系數仍與真值D0有一定偏離,這是近場測試方法具有的系統誤差,這種偏離誤差成為本文研究評估的基本誤差之一.基本誤差之二為基于平面近場測試數據矩陣的數值積分算法本身具有的積分算法誤差.在整個過程中,被測天線方向系數的真值D0是評估的根本參考標準.

本文采用的數值積分數理計算方法本質上是逼近積分真值,總具有一定的數值誤差,不過積分計算程序函數會給出誤差界(error bound),誤差界表示積分逼近值與積分真值的誤差絕對值上界,對同一被積函數,不同方法的誤差界一般不同,誤差界越小,對應方法獲得的積分值越可信,越逼近積分真值,也即收斂性越好;但是數值積分算法無法給出積分真值的確切數值,只能給出由誤差界和積分逼近值決定的一個真值所在區間.這是數值積分的基本特性.

基于上述兩類基本誤差,本文的研究思路為:建立一個可以計算方向系數真值的理論陣列模型,先求其嚴格的方向系數;再按照實際近場掃描系統的掃描范圍與采樣間隔,用計算的方法得到采樣點的場強數據(模擬探頭測量),再用模擬探頭測量的有限離散數據計算方向系數,與理論真值比較,這樣在控制基本誤差之二最小的情況下可評估算法的基本誤差之一的誤差程度,這是對基本誤差之一進行評估.對基本誤差之二進行評估主要依賴于MATLAB函數quad2d()最小積分誤差界的搜索和相關計算.

目前對方向系數的計算算法研究可分為兩類:一類為數值方法,另一類為解析方法.數值方法中一部分文獻在(2)式的基礎上引入簡化假定[4?10],如認為方向圖函數只與θ有關,對積分區間進行截斷處理等;一部分文獻采用計算電磁學的數值方法[11?14]來計算特定屬性天線的電磁場,然后獲得方向系數的仿真解.解析方法中一類文獻聚焦于將方向系數的積分公式進行重新解析分析,如文獻[15]利用電場強度的球面波級數展開和傅里葉級數技術重新分析獲得方向系數的級數表達式,文獻[16]則利用遠場的空間帶寬有限特性,引入采樣技術和插值展開獲得了方向系數的閉式表達式,文獻[17]對一般空間陣列的方向系數進行了解析分析獲得了通用公式.文獻[18]分析了環形微帶貼片天線的方向系數逼近解析公式,也即該公式是近似解析解.文獻[19]專題分析了掃描共線陣列天線的輻射功率和方向系數.這些文獻有一個共同特點:分別計算輻射強度和輻射功率,再得出方向系數,而不是只關注歸一化方向圖函數 F(θ,φ),這點是與本文不同的地方.

但是,基于天線平面近場測試理論、數據、FFT算法和數值積分的通用的方向系數計算求解方法研究文獻報道很少,針對基本誤差二,本文試圖研究一類基于前述理論和技術的逼近數值積分真值的數學物理計算方法,對算法計算誤差源進行深入分析,提出盡可能減小誤差、逼近積分真值的較準確計算方案,然后將積分計算結果與近場被測天線真實方向系數進行比較,以評估這類算法的系統誤差,為理論和實際應用提供參考.本文研究方法屬于數值方法,不是解析方法,與上述參考文獻研究方向合在一起構成方向系數計算算法的兩類方向.

2 計算原理

根據平面近場測試理論[2],任一天線的方向圖函數和方向系數評估都可以基于平面近場測試探頭掃描采樣點矩陣數據進行,對天線方向系數的求解轉變為基于對應掃描采樣點矩陣的近場測試數據矩陣的計算求解.

針對基本誤差之一分析,需要從被測天線模擬出探頭掃描有限采樣平面處的探頭輸出值,根據文獻[2],采用圖1坐標系,探頭輸出值為

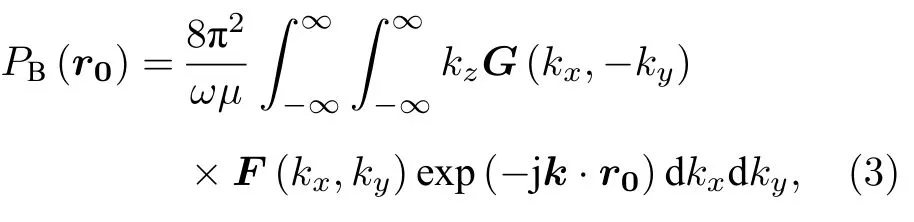
式中kx和ky是二重積分的自變量,有如下關系式:

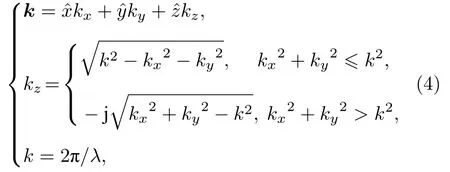
G(kx,–ky)為探頭的平面波譜矢量,F(kx,ky)為被測天線的平面波譜矢量,r0為掃描平面的探頭位置矢量,又因為任一天線的平面波譜矢量A(kx,ky)和其遠場E(r)有如下關系[2]:

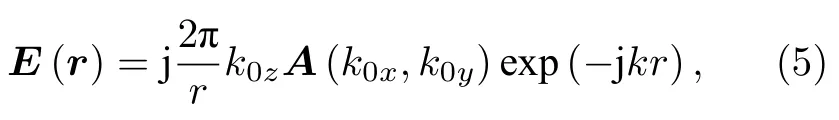
式中 k0為對應遠場點 r(r,θ,φ)方向 (θ,φ)的矢量,有如下關系式:

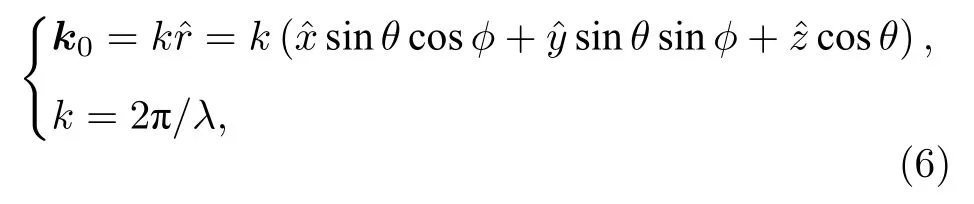
式中 K0z為 K0的 z 向分量,K0z=k cosθ,其他分量含義類似.根據(5)式,任一天線遠場矢量方向圖函數 P(θ,φ)與其平面波譜 A(Kx,Ky)有如下關系:

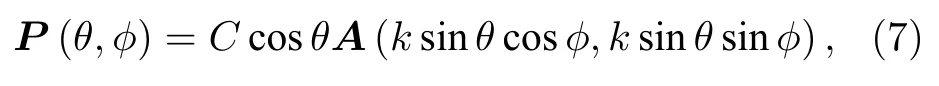
式中C為與θ,φ無關的部分,k為波數大小.

根據(7)式,只要知道了被測天線和探頭的方向圖函數,即可獲知它們對應的位于半徑為k的圓內區域的平面波譜函數,考慮到平面波譜的凋落波成分,在平面近場測試條件下根據(3)式可獲得探頭輸出值.為了簡化計算和提高測量及計算的精度,在探頭與被測天線同為線極化且方向都平行于z軸的情形下(參見圖1,這也是實際近場測試常見的配置,此時被測天線和探頭主極化都為eθ方向),為了(3)式有效采樣離散化來模擬掃描平面處的探頭響應值,可設探頭矢量方向圖函數為 cosθeθ,被測天線方向圖函數為 f(θ,φ)eθ,eθ為球面坐標系對應θ的基矢,根據(7)式,(3)式成為

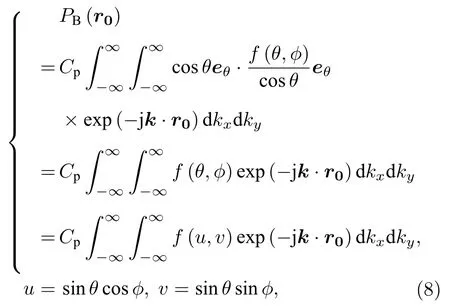
式中 Cp為與 θ,φ 無關的部分,Kx,Ky與 θ,φ 關系如下:

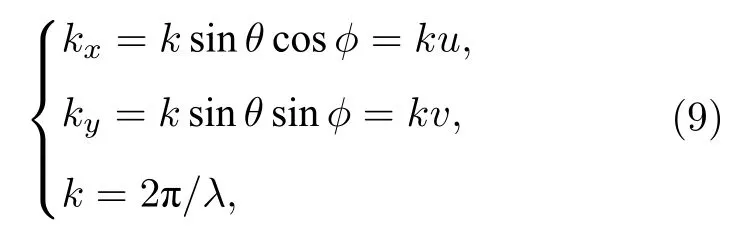
(8)式在平面近場測試條件下進行采樣離散和截斷[20],省掉Cp,有如下關系式:

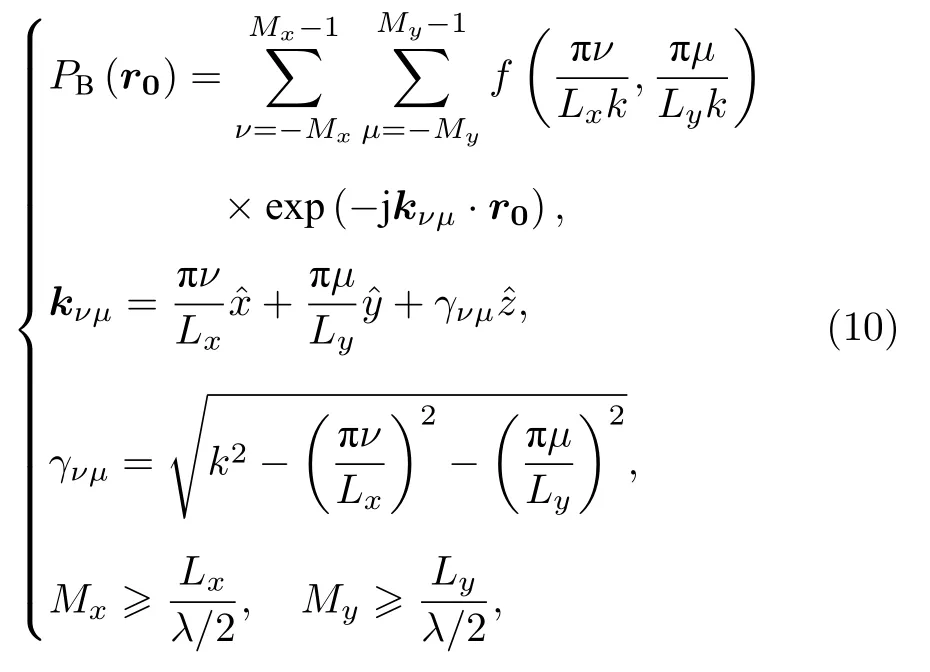
式中Lx為掃描平面x向長度的一半,Ly為掃描平面y向長度的一半,Mx為掃描平面x向采樣點數的一半,My為掃描平面y向采樣點數的一半,為包括所有的傳輸波譜,Mx和My在Lx和Ly確定后需滿足(10)式中的不等式.

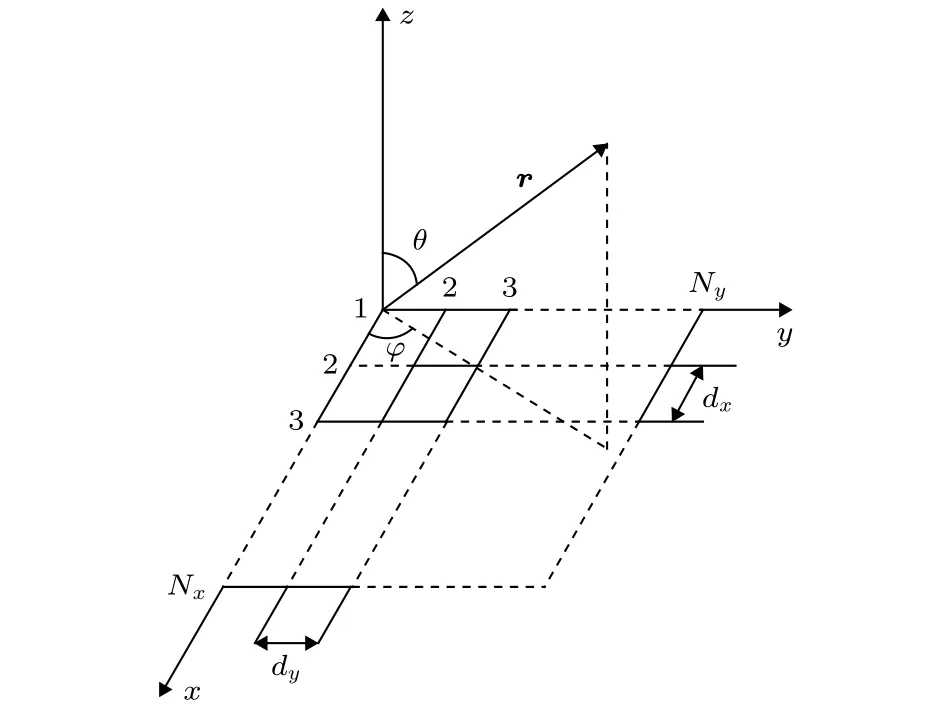
圖1 矩形陣列天線方向圖函數求解坐標系Fig.1.The solution coordinate for the pattern of planar array antennas.

給定一個已知準確方向圖函數 f(θ,φ) (即f(u,v))和準確方向系數D0的被測天線(本文數值算例部分選定一個平面陣列天線作為評估對象,該天線陣列根據文獻[17]可計算出本文條件下的準確方向系數),根據(10)式求解出探頭輸出值后,再根據平面近場測試理論和前述被測天線和探頭極化假定后有如下關系式[2]:

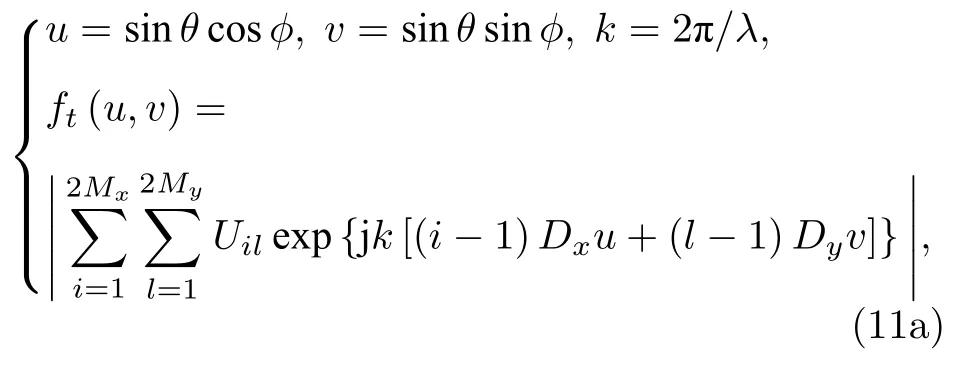
式中ft(u,v)為由被測天線平面近場測試數據計算出的方向圖函數,Dx為掃描平面x向探頭采樣間距,Dy為掃描平面 y 向探頭采樣間距.ft(u,v)與f(u,v)之間存在著一定的系統誤差,本文將在后節數值算例部分對由此導致的方向系數誤差給出評估.

(11a)式中Uil為PB(r0)在采樣點處的離散值,這一近場測試掃描采樣平面矩陣相當于一個平面矩形陣列天線(因為其方向圖表達式與對應的單元位于采樣點并且單元電壓激勵與采樣點探頭輸出值相同的平面矩形陣列天線方向圖表達式陣因子完全一致).一般矩形陣列天線的示意圖如圖1所示,選取矩形陣列平面為xy平面,陣列平面每個交點數據代表一個天線單元(單元結構一樣,只是每個單元激發的電壓或電流幅相可能不一樣).陣列單元數為 Nx×Ny個,沿 x和y 軸的單元間距分別為 dx和 dy,而 (θ,φ)為空間電磁場場點 r 的球坐標方向角.

類似地,針對圖1的結構參數,單元各向同方向性的該平面天線陣列的方向圖函數為[1]

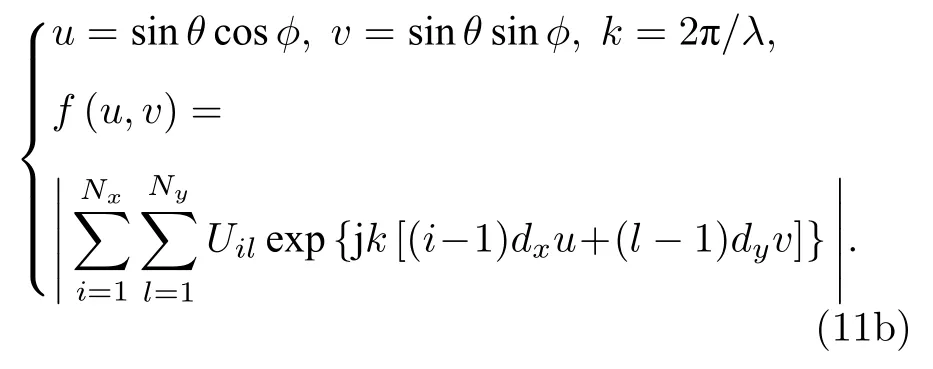
這里f(u,v)無下標t,表示這是平面天線陣列的理論方向圖函數.

近場測試中,利用FFT從平面近場數據矩陣得到的方向圖函數通常是直角坐標形式Ft(u,v),這里使用下標t表示該函數是測試數據產生的方向圖函數,與(11a)式的未歸一化方向圖函數ft(u,v) 相對應.直角坐標變量 (u,v) 對應于球坐標中單位球面上某點在xy平面上的投影坐標,它們的絕對值都不大于1.注意(u,v)實際上只代表上半球面或下半球面上的空間方向,滿足如下關系式[3]:

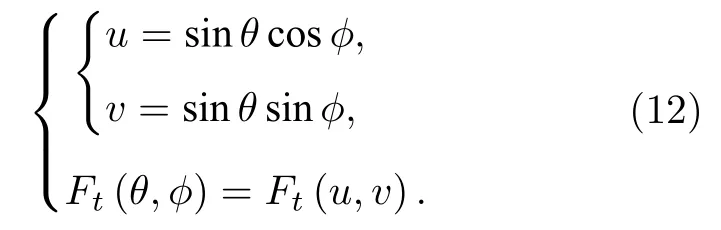
如前所述,根據平面近場測試理論結果的半空間范圍特性,結合天線實際設計與應用,可以認為平面天線陣只具有前向輻射,無需考慮后向輻射,故 Ft(θ,φ)的 θ只取區間 [0,π/2],方向系數寫為Dpa,表達式 (2)式修正為

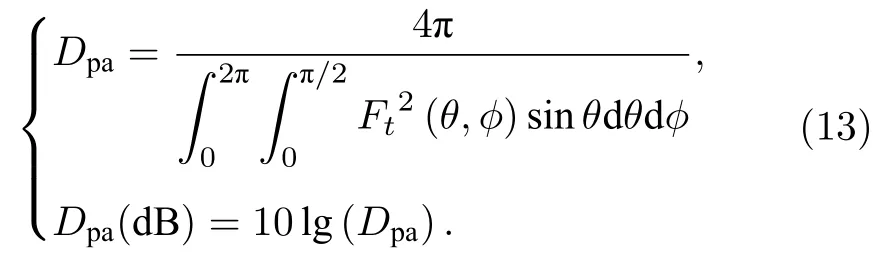
設有一被積函數 H(u,v),滿足

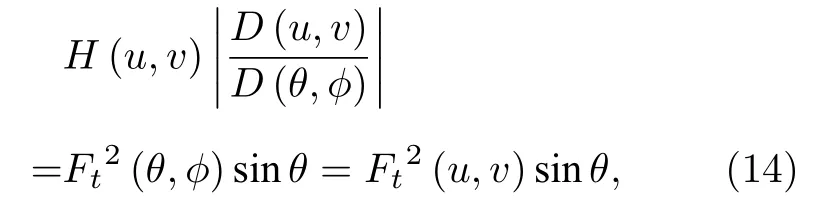
式中 |···| 為雅可比行列式,是被積函數積分元變換的基本因子,可以寫為

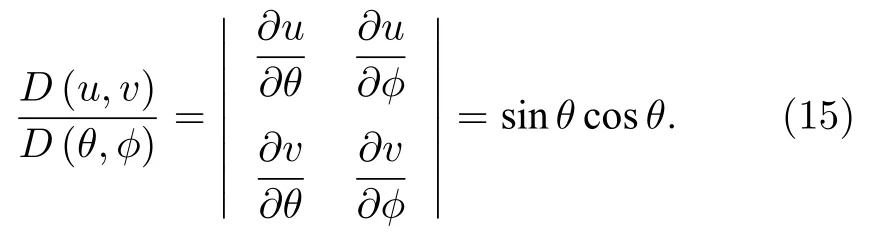
根據 (12)式,有

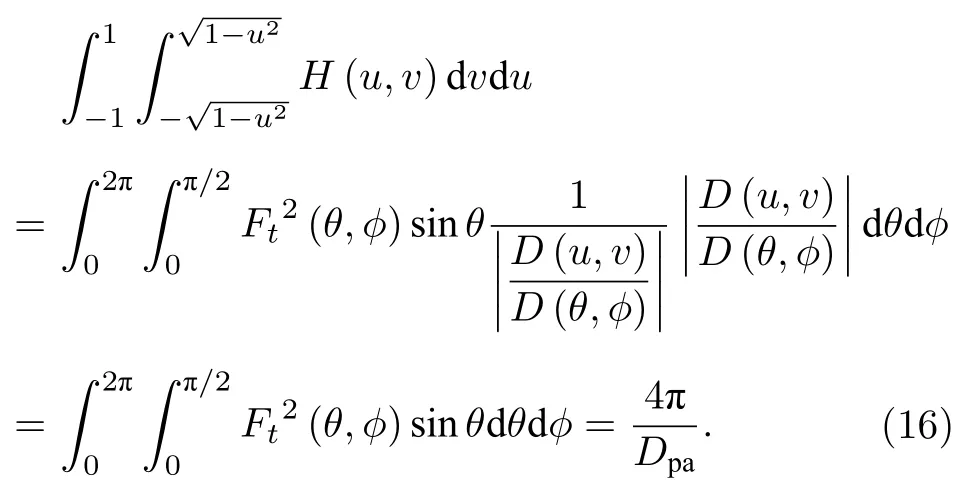
根據 (14)式、(15)式和 (12)式,有

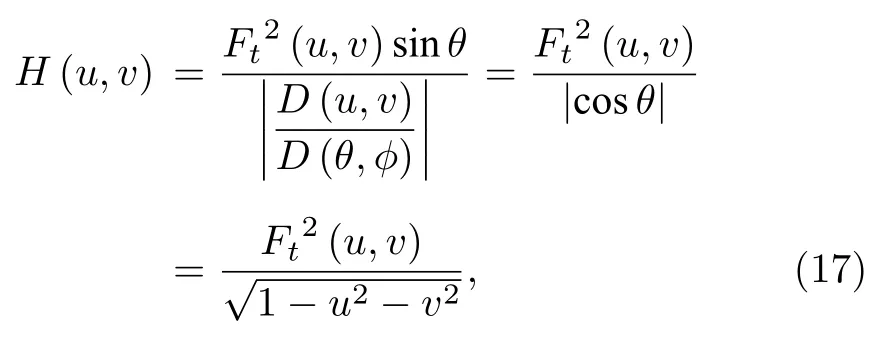
很顯然,(13)式可重寫為

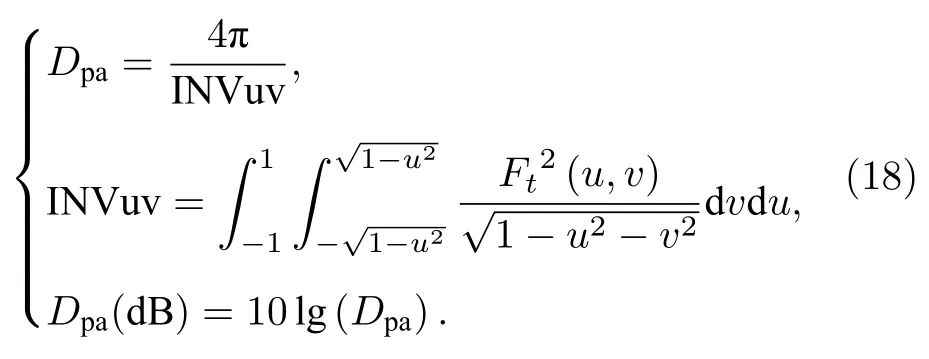
本文基本誤差之二問題最后變成逼近計算近場測試數據矩陣方向系數(18)式的問題.基于PNF程序的算法可以快速計算平面近場測試數據的方向系數,但所得系數Dpa沒有精度控制,無法估計計算結果的可靠性.本文將在(18)式基礎上引入數值積分精度控制,實現可靠逼近INVuv的真值,也就是實現可靠逼近近場測試數據矩陣方向系數積分式真值.

3 數值積分算法自身精度分析

為研究各種計算INVuv的方法,本文主要采用體現各種算法內核的程序數值仿真形式,分析誤差來源,給出積分逼近值、誤差界和積分真值所在區間,進行仿真驗證、評估.共討論四種逼近方法.

1) PNF:作者所在單位專業科技人員開發的程序,作為一種近場數據處理程序得到廣泛使用,本文將其作為參考評估基礎.它的方向系數算法類型肯定屬于數值積分,但是因為PNF是編譯后可執行程序,具體算法未知,只能通過與其他算法的結果進行比較來分析、評價其準確性和快速性.

2) 本文所述的FFT算法[3]基礎積分估算程序,無精度控制.其基本點是在已知矩形陣列幅相分布基礎上,利用FFT算法快速算出陣面方向圖函數 Ft(u,v).該方法提供了有限的、離散的 (u,v)處函數值,然后基于對函數Ft(u,v)特性的分析來數值求積求和逼近INVuv.此方法由于積分數據受FFT算法限制,計算所覆蓋的u值范圍未完全覆蓋積分定義域 [–1,1],因此 INVuv 在 (u,v)定義域邊緣處的積分值被忽略掉,導致INVuv偏小.另外,近似數值求積求和也引入了一定計算誤差.此方法的結果誤差界要通過與以下兩種方法尤其是第4)種方法的比較才能有一定的估計,正是由于它沒有誤差控制,因此計算時間在第 2),3),4)種方法中是最短的,也即速度在三種方法中最快.

3) 在第 2)種方法基礎上,引入 MATLAB二維插值函數interp2()和二維數值積分基本函數quad2d()的積分程序.積分基本函數quad2d()提供誤差容差控制,積分方法是平鋪(tiled),不是兩次一重積分迭代(iterated),平鋪的基本方法是將非矩形平面積分區域通過內部變換函數變換為一批小矩形積分區域再進行數值求積,而且quad2d()函數能處理積分區域邊界處的被積函數暇點,這種能力正好適應(18)式中被積函數在積分邊界處的暇點特性,具體信息可參閱文獻 [21].一般來說,這一方法的積分結果比第2)種方法的結果更逼近積分真值,它在第2)種方法得到的Ft(u,v)離散值基礎上進行二維插值,來估算所需插值點處的函數值.這些插值點由求積函數quad2d()根據積分算法需要產生,從而使本方法獲得了更多的被積函數值.這些插值點處的被積函數值相對于函數值真值來說仍存在一定插值誤差,雖然經過MATLAB的三次Hermite或樣條插值方法可盡量逼近函數值真值,但插值誤差不可能完全消除.

4) 基于累加求和的 Ft(u,v)積分計算,稱為累加求和被積函數解析值方法.注意到被積函數Ft(u,v)的“未歸一化”累加求和解析表達式 ft(u,v)即為(11a)式:

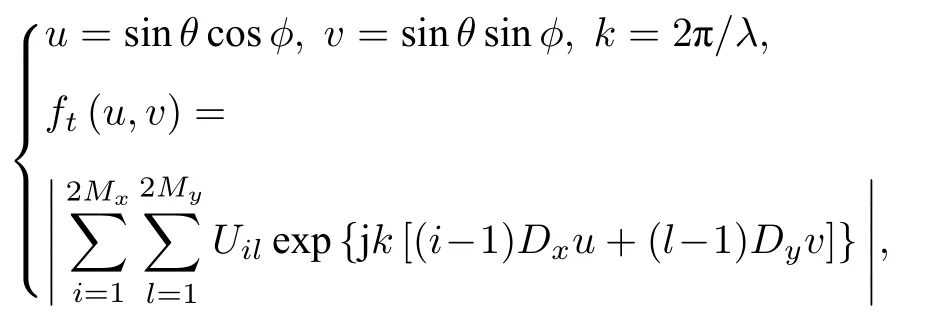
式中Uil為PB(r0)在采樣點處的離散值,Uil也可理解為探頭采樣平面對應的平面矩形陣列天線離散單元處激發的電壓或電流的幅相復數值.Ft(u,v)與 ft(u,v)關系為

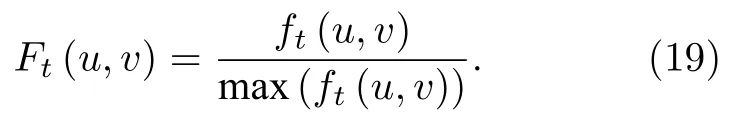
很顯然,要得到 Ft(u,v)的值,必須知道 ft(u,v)的最大值.有兩種方法:一是由第2)種方法得到的主瓣位置 (u0,v0)(即 ft(u,v)最大值所在方向)代入(19)式求得.這里,得到的最大值因為是離散數據,在第2)種方法二維FFT計算點數(一般取為210×210)較多的情形下只有一定的微小誤差;二是理論分析得到ft(u,v)函數最大值,比如圖1相控陣的最大值方向(u0,v0)在某些情形下可有理論分析值,代入 (11a)式即可獲得 ft(u,v)函數最大值,這一方法沒有函數值誤差.雖然理論分析法精度更高,但是理論分析值可應用情形不多,第一種方法是(11a)式獲得最大值的通用方法.

根據(11)式、(18)式和(19)式,本方法引入MATLAB二維數值積分基本函數quad2d()的積分程序來計算積分值.該方法與第3)種方法不同之處在于被積函數即為根據近場測試理論得出的Ft(u,v)解析表達式,而第 3)種方法中,被積函數Ft(u,v)的值來源于被插值 (u,v)處的估計值,引入了插值誤差.本方法避免了數值計算Ft(u,v)這一影響積分精度的關鍵因子時引入的誤差,直接引入Ft(u,v)累加求和解析表達式.該方法根本誤差源只有一項:來源于MATLAB二維數值求積函數quad2d()的計算精度誤差,因此在同樣容差精度條件下其結果是最逼近積分真值的,雖然計算耗時最長.

本文基于MATLAB和其包含的二維數值積分基本函數quad2d()開發了數值積分計算天線方向系數的程序,程序中根據quad2d()函數返回的信息不斷調節計算容差,實現最小容差定位和最佳積分逼近值,同時給出誤差界和積分真值區間.誤差界越小,積分值越逼近積分真值.需要說明的是,此處積分真值與被測天線方向系數真值是不同的概念,兩者之間如前所述有一定的系統偏離.

鑒于以上分析和論證,方法4)可作為對于同一被積函數不同數值積分算法關于積分真值的參考基準,數值算例和結果可以予以驗證,算例結果應體現在同樣被積函數條件下方法4)的誤差界最小,方法4)是積分真值的最佳逼近.

綜上所述,對于第1)種方法,只能將其計算結果與其他三種方法進行誤差比較來給出評估;第2),3)種方法可以用第4)種方法的結果作為評估積分真值本身的參考基準,這點將由下節的數值算例和結果驗證.

4 數值算例與結果

為了比較這四種方法的結果,本文選取某個矩形陣列天線作為被測天線,矩形陣列天線示意圖如圖1 所示.矩形陣列結構參數為:Nx=60,Ny=40,dx=0.65λ,dy=0.65λ,λ 為計算輻射電磁波波長.結合實際精度和速度需要,二維FFT計算點數一般設為210×210.這一陣列將作為以下7個算例的平面近場測試被測天線(單元各向同方向性),它的方向圖函數和方向系數真值都可獲得.文獻[17]給出了任意立體陣列的方向系數解析解,自然本被測天線也包含在內,結合平面近場測試的測試條件和假定,單元各向同方向性的相位線性遞增分布的平面天線陣列方向系數有如下表達式[17]:

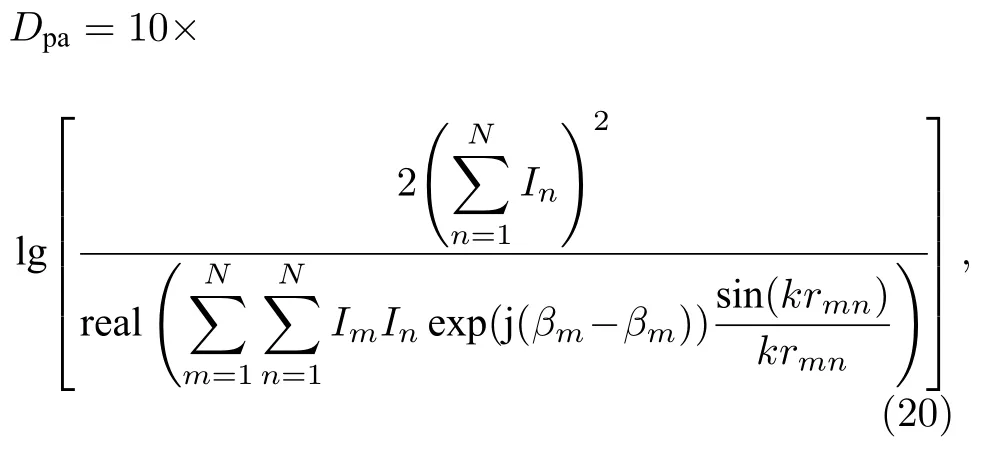
式中N表示天線陣列的單元總數,I表示單元激勵電流或電壓振幅值,β表示單元激勵電流或電壓相位值 (弧度),k 為波數,m和n 是單元下標,rmn表示單元m和單元n之間的空間距離,real表示取復數實部.下文算例1至算例4天線陣列屬于這一類別.

類似地,單元各向同方向性的相位任意分布的天線陣列的方向系數有如下表達式[17]:

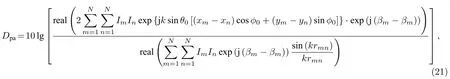
式中 x和y 是單元的直角坐標值,(θ0,φ0)為根據第3節第2)種方法求解出的方向圖函數最大值球坐標方向角,其他物理量含義同(20)式.下文算例5至算例7天線陣列屬于這一類別.

被測天線與探頭掃描采樣平面距離d0=3λ,(10)式中有關結構參數如下:Lx=Nx·dx=39λ,Ly=Ny·dy=26λ,采樣間距 Dx=0.5λ,Dy=0.5λ,Mx,My由 (10)式給出為 Mx=78,My=52.

本文共針對7個算例展開數值仿真計算,7個算例給定的電壓激勵模式都是針對矩形陣列被測天線,電壓激勵模式選擇遵循如下原則:盡量覆蓋方向系數高、低的情形,同時結合天線電訊設計工程實際中常用的電壓激勵幅相分布,以全面評估、驗證、判斷這四種方法哪一種計算的方向系數Dpa的準確性最好.計算過程簡介如下:先由(10)式模擬算出被測天線在探頭采樣平面的激勵電壓值,再由(11a)式和(18)式等對模擬探頭測試數據矩陣進行四種方法的數值積分計算,并將結果與被測天線的方向系數理論真值進行比較,從而獲得近場測試數據方法計算方向系數的誤差評估結果,具體如以下7個算例所示.

本文的計算機軟硬件環境配置如下:操作系統為 Windows 7 SP 1 X64 旗艦版,內存 4 GB,處理器Intel Core2 Duo CPU P9400@2.4GHz,MATLAB版本為 8.1.0.604(R2013a) 32-bit(Win32).第 1)種方法為Windows可執行程序,計時采用秒表;第2),3),4)種方法為 MATLAB 程序,可在程序中精確計時,quad2d()函數初始絕對誤差控制為10–7,該值不同,第 3),4)種方法耗時會不同.四種方法都在上述同一計算平臺進行驗證評估.

算例1激勵模式滿足幅度均勻分布、相位同相的條件.理論分析可知主瓣波束指向(即方向圖函數最大值方向)滿足 (θ0,φ0)=(0°,0°),即指向陣面法向.此時,數值積分時不存在 ft(u,v) 函數最大值誤差.這種幅相分布稱為幅相均勻分布,在工程實際應用中,雷達天線發射通常采用這種幅相分布.其特點是方向圖波束寬度很窄,副瓣電平為–13.3 dB 左右,方向系數較大.對此分布,利用(20)式被測天線方向系數理論真值公式和所列四種方法對近場測試矩陣的計算和評估結果如表1所列.計算結果表明,天線陣列方向系數達到40 dB 以上,實現了高方向性,與均勻分布的規律一致.

算例2激勵模式滿足幅度均勻分布條件,但相位則依x軸、y軸可分離線性遞增分布(廣義遞增,相鄰單元相位增量為負也叫遞增).這種相位分布是典型的相控陣掃描相位分布,在工程實際中廣泛應用,能實現相控陣波束掃描功能.本例設定波束掃描指向為 (θ0,φ0)=(40°,–60°),即在算例 1的基礎上實現相控陣波束掃描,也就是主瓣波束掃向空間方向 (θ0,φ0)=(40°,–60°).相比于 (θ0,φ0)=(0°,0°)的情況,這一相控陣掃描陣列方向系數要小,且掃描角偏離 (θ0,φ0)=(0°,0°) 越大,方向系數就越小.針對此分布的四種方法計算與評估結果如表2所列.計算結果表明,本例相控陣掃描陣列方向系數比算例1的情形下降2.0 dB左右.

算例3激勵的幅相遵循常用的Taylor分布.在相同副瓣電平設計要求的條件下,Taylor分布易于在實際工程中實現.工程實際中,此分布一般用于天線接收時的幅相分布設計.本例假定幅度在 x方向為–35 dB 副瓣電平的 Taylor分布,在y 方向為–25 dB 副瓣電平的 Taylor分布,相位掃描波束指向為 (θ0,φ0)=(40°,–60°).針對此分布的四種方法計算和評估結果如表3所列.

算例4FFT計算精度的影響.在算例3基礎上,將FFT算法分辨率進一步提高,一維FFT點數由210變為211,注意本文所指FFT實際上是二維FFT運算.因為Ft(u,v)的真實離散值數量同步增大,數值積分計算結果一般會更加逼近真值.但是,FFT點數不宜太多,否則計算逼近時間太長,不便實用,如本例第 3)種方法耗時太多.在此情況下,考察積分結果的變化,四種方法計算和評估結果如表4所列.

算例5幅度、相位隨機“均勻”分布誤差的影響.以上算例為高方向性的計算實例,在其基礎上,可以研究低方向性情況下的性能.一種可能性為在上述幅相分布的基礎上引入隨機幅相分布誤差,因此本算例在算例3的基礎上引入幅度、相位隨機“均勻”分布誤差.四種方法計算和評估結果如表5所列.結果表明,隨機均勻分布幅相誤差對矩形陣列天線的方向系數數值影響很大(方向系數降低24 dB左右),實現了低方向性矩形陣列幅相分布.注意到PNF更加逼近方向系數真值.

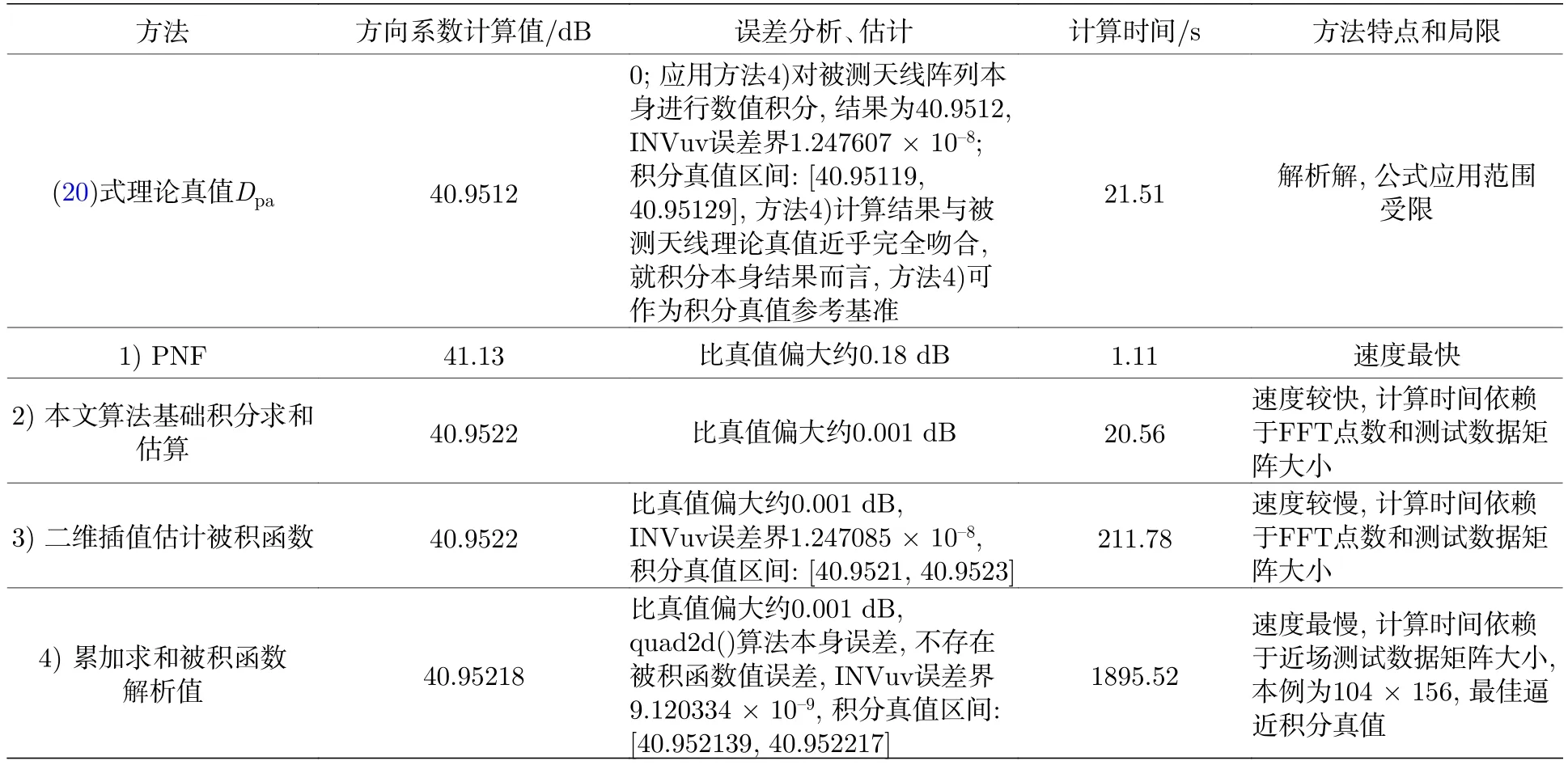
表1 激勵均勻分布四種方法方向系數計算比較評估Table 1.Comparison and evaluation of four computation methods of directivity in uniform distribution of electromagnetic excitation.

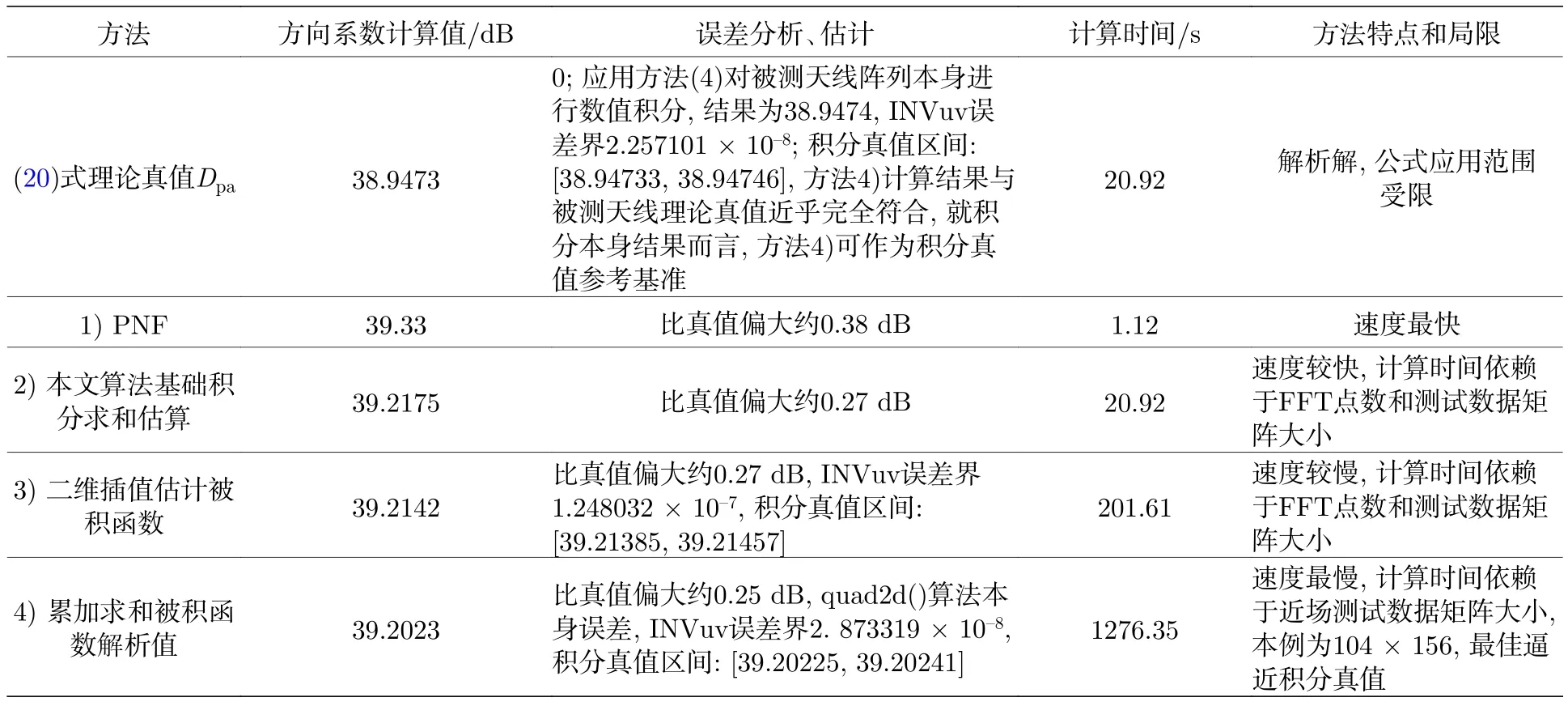
表2 激勵幅度均勻相位掃描分布四種方法方向系數計算比較評估Table 2.Comparison and evaluation of four computation methods of directivity in uniform amplitude &linear scanning phase distribution of electromagnetic excitation.

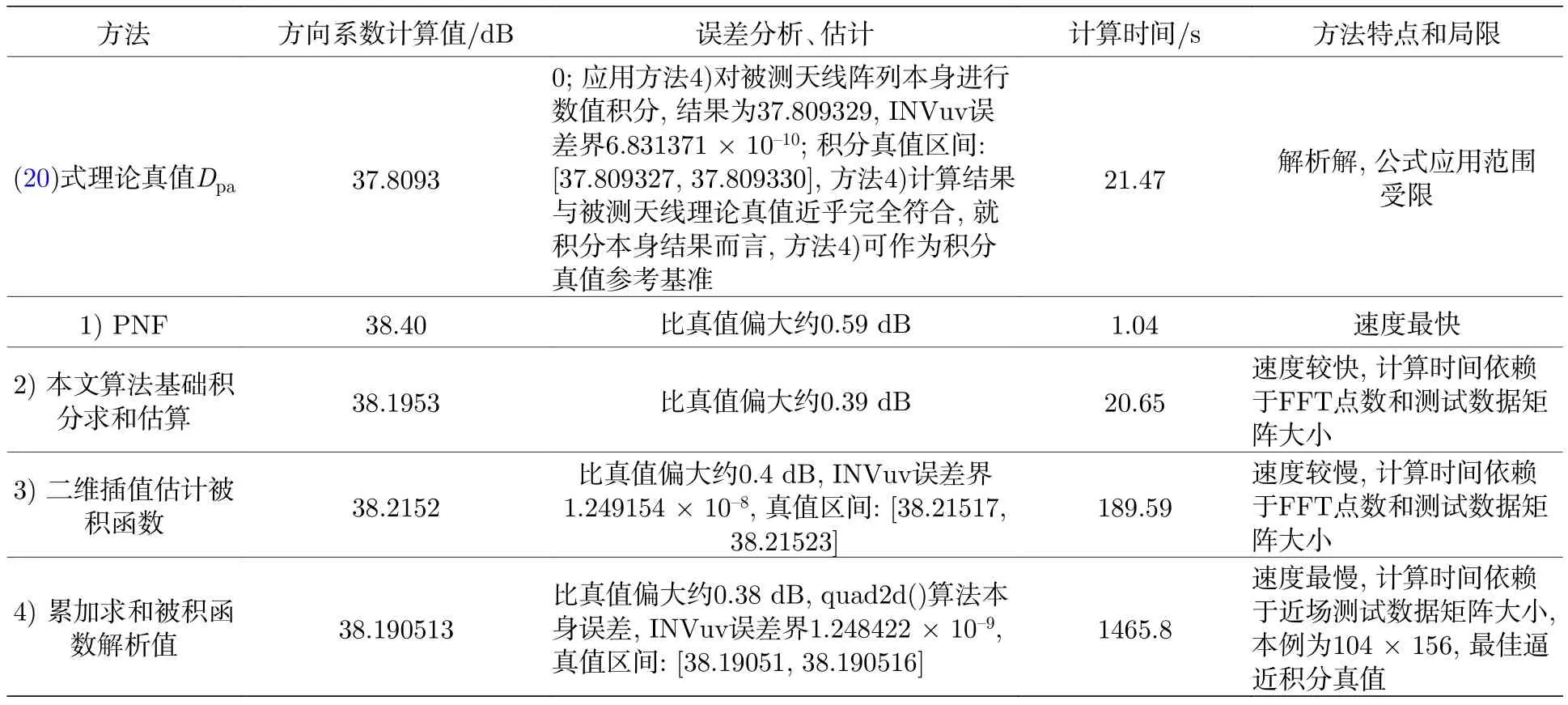
表3 激勵Taylor分布四種方法方向系數計算比較評估Table 3.Comparison and evaluation of four computation methods of directivity in Taylor distribution of electromagnetic excitation.

算例 6幅度、相位隨機“正態”分布誤差對Taylor分布的影響.在算例3的基礎上,引入幅度、相位隨機“正態”分布誤差.四種方法計算和評估結果如表6所列.結果表明,隨機正態分布幅相誤差對方向系數數值影響顯著(方向系數減小25 dB左右),實現了低方向性矩形陣列幅相分布.注意到PNF更加逼近方向系數真值、速度最快,其他方法逼近積分真值規律和計算速度上與高方向系數的情形類似.

算例7幅度、相位隨機“正態”分布誤差對均勻分布的影響.在算例1基礎上引入幅度、相位隨機“正態”分布誤差,進一步考察較小方向系數的矩形陣列天線.四種方法計算和評估結果如表7所列.四種方法逼近積分真值規律和計算速度上與算例6的情形類似,正態分布誤差對均勻幅相分布的影響比對Taylor分布的影響大,本例方向系數下降27 dB左右.注意到PNF更加逼近方向系數真值.

上述7個算例的計算仿真和評估驗證表明,計算天線方向系數的數值積分四種方法各有特點和局限,如下所述.

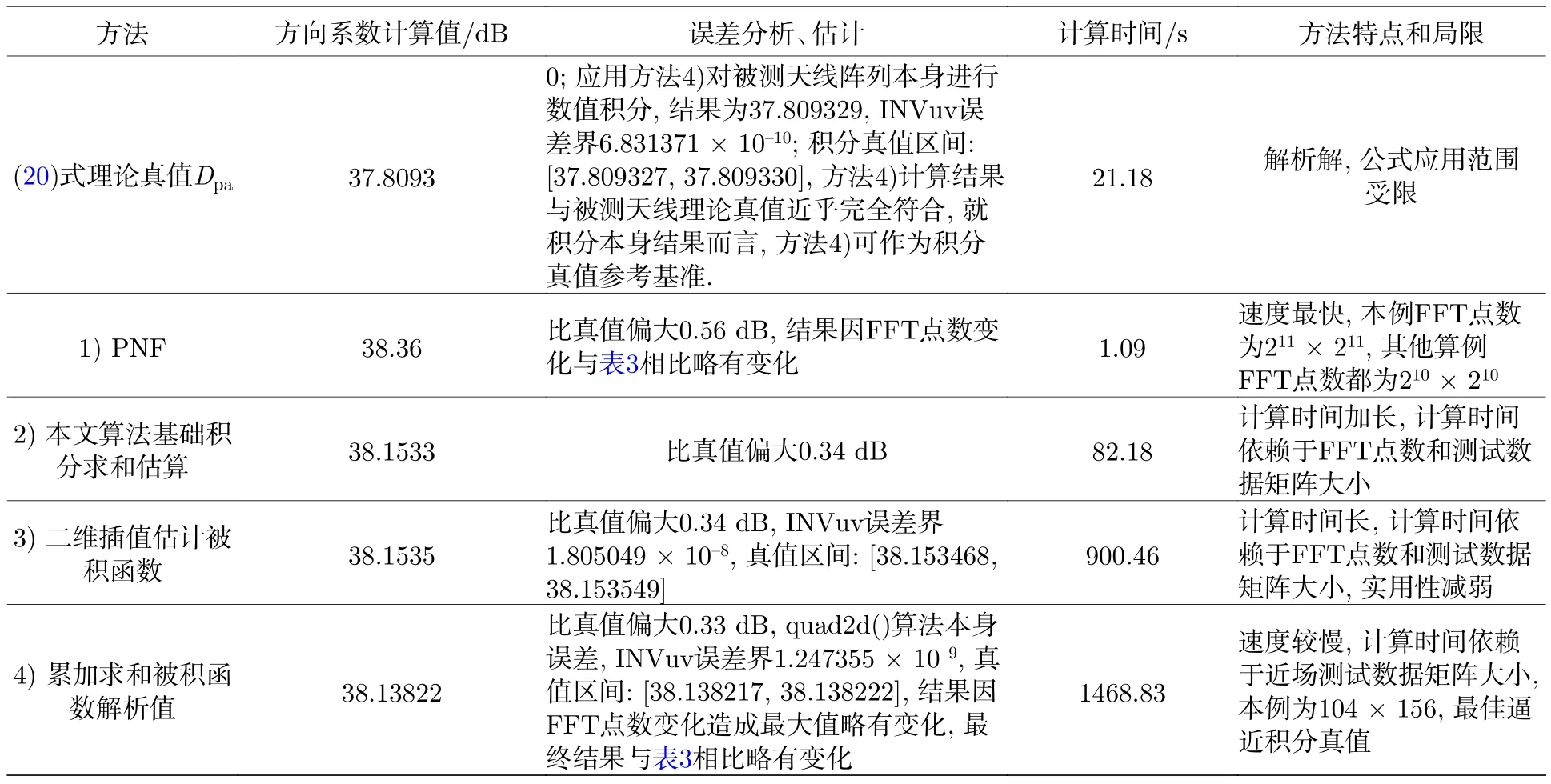
表4 激勵Taylor分布FFT精度提高四種方法方向系數計算比較評估Table 4.Comparison and evaluation of four computation methods of directivity in Taylor distribution of electromagnetic excitation with raised precision of FFT algorithm.

第1)種方法PNF對高方向系數的計算誤差相對較大,誤差較大值接近 0.6 dB,對低方向系數的計算逼近方向系數真值,速度總是最快.這表明PNF計算高方向系數天線時,算法對應INVuv的積分結果比INVuv積分真值偏小,造成計算的方向系數值比第4)種方法計算的方向系數值偏大,因為第4)種方法對應INVuv的積分結果(如算例1—算例7誤差分析、估計部分結果證明)總是INVuv積分本身真值的最佳逼近(近乎完全符合).但是所有方法(包括第4)種方法)計算出的方向系數總是比方向系數真值偏大,這就造成PNF計算的方向系數更加遠離方向系數真值,如算例1—算例4所示.PNF計算低方向系數天線時,算法對應INVuv的積分結果比INVuv積分真值偏大,造成計算的方向系數值比第4)種方法計算的方向系數值偏小,同樣因為第4)種方法對應INVuv的積分結果總是INVuv積分本身真值的最佳逼近(近乎完全符合).但是所有方法(包括第4)種方法)計算出的方向系數總是比方向系數真值偏大,這樣就造成PNF計算的方向系數更加逼近方向系數真值,如算例5—算例7所示.

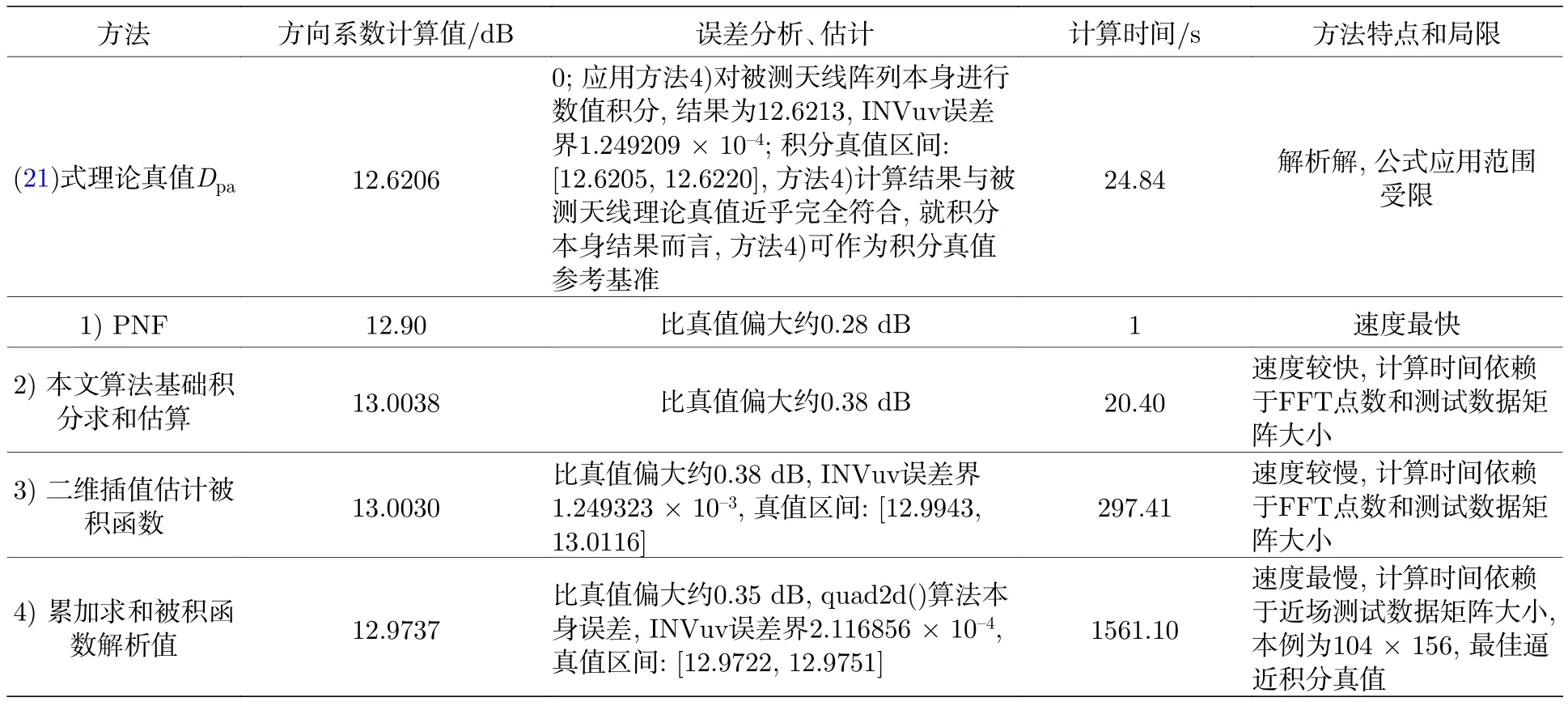
表6 激勵Taylor分布幅相誤差隨機正態分布四種方法方向系數計算比較評估Table 6.Comparison and evaluation of four computation methods of directivity in Taylor distribution of electromagnetic excitation with normal random errors for amplitude &phase.

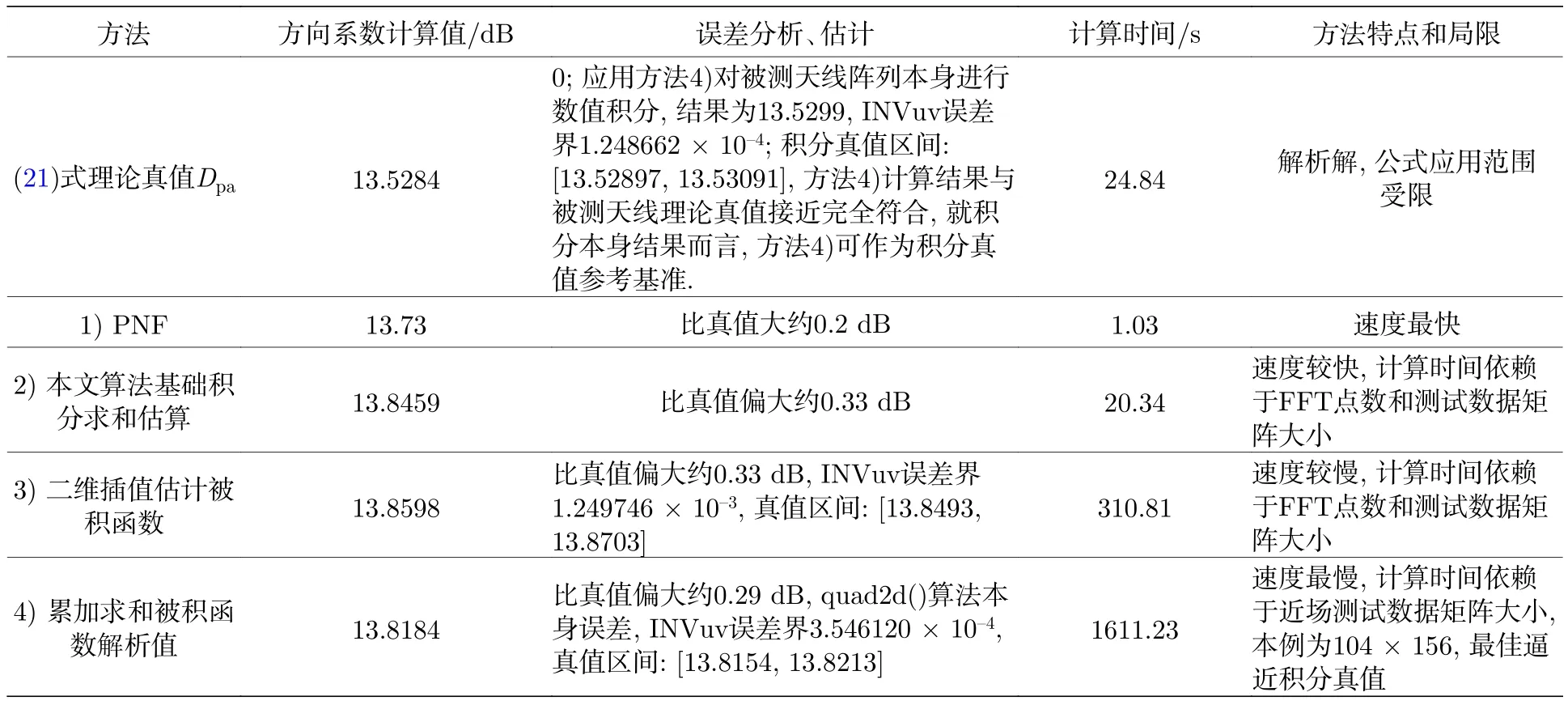
表7 激勵均勻分布幅相誤差隨機正態分布四種方法方向系數計算比較評估Table 7.Comparison and evaluation of four computation methods of directivity in uniform distribution of electromagnetic excitation with normal random errors for amplitude &phase.

第 2)種方法速度稍慢,計算時間依賴于FFT點數和測試數據矩陣大小,對于測試矩陣數據總數在 16000 (104×156=16224)規模,一般計算時間在 20 s左右;第 3)種方法速度更慢,基于第(2)種方法已知的方向圖函數值,引入MATLAB二維插值函數interp2()和二維數值積分基本函數quad2d(),采用三次Hermite插值或樣條插值和二維數值積分精度控制,一般來說使計算結果更加逼近積分真值,第4)種方法根據前面小節的理論分析論證和本小節的數值算例仿真結果驗證,誤差界一般情況下最小,因此可作為積分真值最佳逼近,也可作為其他三種方法積分計算結果本身準確性評估的基礎,該方法根本誤差源只有quad2d()的計算誤差,但是耗時最長.

所有方法計算結果都比被測天線方向系數真值偏大.其中PNF對于高方向性天線計算誤差最大值達 0.6 dB;對于低方向性天線,計算結果更加逼近方向系數真值.第 2),3),4)種方法計算誤差最大值為 0.4 dB,在這三種方法中,第 4)種方法誤差最小.在四種方法中,第4)種方法總是積分本身真值的最佳逼近,但是耗時最長.

5 結 論

基于平面近場測試理論獲得的矩形陣列幅相數據,利用MATLAB插值函數和數值積分函數對被測天線的方向系數進行了逼近求解.提出了三種新的近場測試數據數值積分計算方法,并與已有的PNF計算程序進行了仿真數據對比,給出了這些方法的特點和局限.結果顯示:所有方法計算結果都比被測天線方向系數真值偏大.其中第1)種方法PNF對于高方向性天線計算誤差最大值達0.6 dB;對于低方向性天線,計算結果更加逼近方向系數真值.第2)、第3)、第4)種方法計算誤差最大值為 0.4 dB,在這三種方法中,第 4)種方法誤差最小.在四種方法中,第4)種方法總是積分本身真值的最佳逼近,但是耗時最長.第1)種方法PNF速度總是最快.第2)種方法FFT算法基礎積分估算程序速度稍慢,但是計算誤差對于高方向系數情形較小.第3)種方法基于MATLAB插值函數interp2()和數值積分函數quad2d()的積分程序一般來說比第2)種方法計算精度更高,速度較慢,積分結果一般來說相對于第2)種方法更加逼近方向系數真值.第4)種方法累加求和被積函數解析值方法可作為方向系數積分式本身真值的最佳逼近,相比于第2)種、第3)種方法離被測天線方向系數真值更近,但是耗時最長,不大能滿足快速響應的需求.本工作是對基于平面近場測試數據的一類天線方向圖和方向系數計算技術的系統評估,對天線方向系數的計算數理方法研究具有理論和應用價值.