雙層耦合非對稱反應擴散系統(tǒng)中的超點陣斑圖*

劉富成 劉雅慧 周志向 郭雪 董夢菲

(河北大學物理科學與技術(shù)學院,保定 071002)

通過線性耦合Brusselator模型和Lengyel-Epstein模型,數(shù)值研究了雙層耦合非對稱反應擴散系統(tǒng)中圖靈模之間的相互作用以及斑圖的形成機理.模擬結(jié)果表明,合適的波數(shù)比以及相同的對稱性是兩個圖靈模之間達到空間共振的必要條件,而耦合強度則直接影響了圖靈斑圖的振幅大小.為了保證對稱性相同,兩個圖靈模的本征值高度要位于一定的范圍內(nèi).只有失穩(wěn)模為長波模時,才能對另一個圖靈模產(chǎn)生調(diào)制作用,并形成多尺度時空斑圖.隨著波數(shù)比的增加,短波模子系統(tǒng)依次經(jīng)歷黑眼斑圖、白眼斑圖以及時序振蕩六邊形斑圖的轉(zhuǎn)變.研究表明失穩(wěn)圖靈模與處于短波不穩(wěn)定區(qū)域的高階諧波模之間的共振是產(chǎn)生時序振蕩六邊形的主要原因.

1 引 言

自組織斑圖是非線性動力學系統(tǒng)的一個典型特征,普遍存在于自然界以及眾多非線性系統(tǒng)中,例如物理、化學以及生物系統(tǒng)等[1-6].在過去的半個世紀內(nèi),人們對斑圖形成機理的認識有了突飛猛進的發(fā)展,其中比較著名的就是反應擴散系統(tǒng)的圖靈機制[7],一個均勻穩(wěn)定態(tài)經(jīng)歷圖靈失穩(wěn)后會產(chǎn)生不隨時間變化的空間周期性分布的結(jié)構(gòu),例如條紋斑圖和六邊形斑圖[8,9].

近年來,多層耦合系統(tǒng)中不同模式之間的相互作用越來越受到人們的關(guān)注[10-18],其中不同圖靈模之間的相互作用可以產(chǎn)生各種復雜的多尺度時空斑圖.2002年,Yang等[11]通過線性耦合雙層反應擴散系統(tǒng)研究了圖靈模之間的相互作用,結(jié)果表明圖靈模之間的波數(shù)比、子斑圖對稱性以及本征值高度是空間共振的三個必要條件.該研究小組還發(fā)現(xiàn)僅僅是雙層間的耦合作用也可以導致一種新的叉形分叉,進而產(chǎn)生兩個圖靈模式.這兩個圖靈模相互作用可以形成對稱、非對稱以及反相圖靈斑圖[12].在此基礎(chǔ)上,多個研究小組對圖靈模相互作用機理進行了進一步研究.例如Liu等[13]在更廣的本征值高度范圍內(nèi)獲得了超點陣斑圖,并且在波數(shù)比接近4∶1時觀察到一種新類型的白眼斑圖.Catlla等[14]發(fā)現(xiàn)當兩個圖靈模的波數(shù)比例為時,系統(tǒng)可以產(chǎn)生穩(wěn)定的四邊形斑圖.白占國等[15-18]詳細研究了各種耦合條件對斑圖的影響,發(fā)現(xiàn)了多種超點陣四邊形斑圖,包括大小點、白眼、點線和復雜超四邊等.

以前的研究主要集中在相同反應擴散模型[19-27]之間的耦合,例如兩個Brusselator模型[19,20]、兩個Lengyel-Epstein模型[21-23]或者是兩個Oregonator模型[24]等.在大多數(shù)非線性系統(tǒng)中,同時存在著多種不同的非線性物理過程,這些過程各自具有不同的斑圖形成機理.例如在介質(zhì)阻擋放電系統(tǒng)中,放電層與電介質(zhì)層相互耦合,可以產(chǎn)生種類繁多的時空斑圖,這些時空斑圖通常由兩套或者多套子結(jié)構(gòu)相互嵌套而成[25-27],因此有必要對不同物理過程之間的耦合進行詳細研究.然而到目前為止,不同反應模型之間的耦合以及斑圖選擇機制還尚未見報道,人們對不同斑圖形成系統(tǒng)之間的耦合機制還不甚清楚.

本文通過線性耦合兩個不同的反應擴散模型數(shù)值研究了兩個圖靈模之間的相互作用,并分析了兩個圖靈模的波數(shù)比、相對強度以及耦合強度對斑圖選擇和形成的影響.

2 模型分析

為了研究不同系統(tǒng)形成的圖靈模之間的相互作用,本文采用線性耦合兩個不同的反應擴散模型,構(gòu)建了一個雙層耦合非對稱反應擴散系統(tǒng)模型,在無量綱的情況下,該模型具有以下形式:

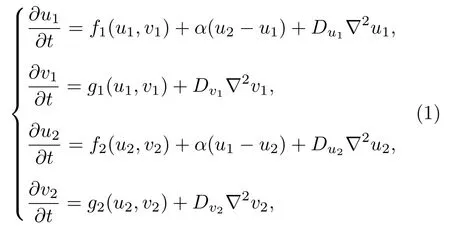
該模型包含兩個子反應擴散系統(tǒng) (u1,v1)和(u2,v2),α為兩個子系統(tǒng)活化子之間的耦合強度;方程f(u,v)和 g (u,v) 為每個子反應擴散系統(tǒng)的局部動力學方程,不同的反應系統(tǒng)有著不同的具體表達式.本文選取Brusselator模型和Lengyel-Epstein模型來充當兩個子系統(tǒng).在無量綱的情況下,Brusselator模型的局部動力學方程具有下列形式:

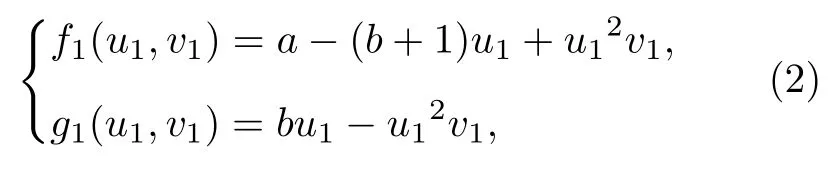
其中系數(shù)a和b是系統(tǒng)的控制參數(shù).

Lengyel-Epstein模型在無量綱情況下的形式為

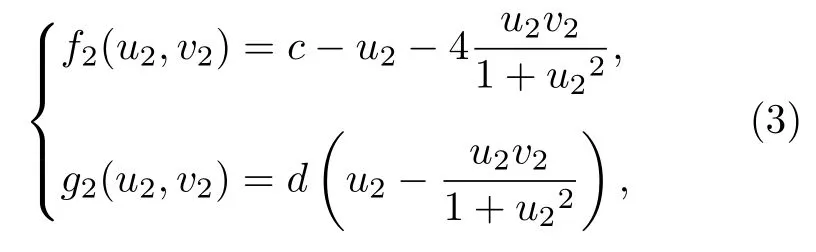
其中系數(shù)c和d是系統(tǒng)的控制參數(shù).對于子系統(tǒng)1和2,其均勻定態(tài)解分別為 (u10,v10)=(a,b/a) 和本文中選取c=5a,則雙層耦合系統(tǒng)的均勻定態(tài)解可以表示為

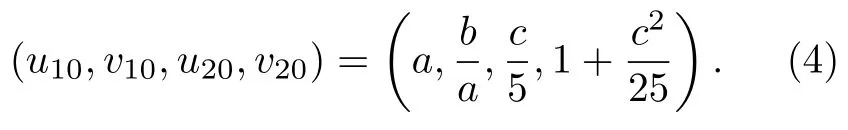
對該均勻定態(tài)解附加一個均勻的線性微擾,去掉高階項得到其線性本征方程:

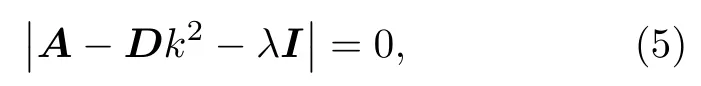
其中A和D分別為雅克比矩陣和擴散系數(shù)矩陣,

解此本征方程可得到本征值λ,本征值λ與微擾模之間的關(guān)系被稱之為系統(tǒng)的色散關(guān)系曲線.通過系統(tǒng)的色散關(guān)系可以分析失穩(wěn)模的性質(zhì)以及系統(tǒng)的分岔類型.

圖1給出了兩個耦合系統(tǒng)處于圖靈空間時的色散關(guān)系.圖1中藍色實線為本征值的實部,代表模式的線性增長率,紅色虛線為本征值的虛部.對于每一個子系統(tǒng),當活化子u的擴散系數(shù)遠小于禁阻子v的擴散系數(shù)時,系統(tǒng)經(jīng)歷圖靈分岔并激發(fā)出圖靈模.該圖靈模的波數(shù)大小為其中Δ是與控制參數(shù)有關(guān)的常數(shù).Du相比于 Dv越小,系統(tǒng)偏離分岔點越遠,圖靈模線性增長率越高,即圖靈模的本征值高度越高.因此通過調(diào)節(jié)模型中各變量的擴散系數(shù),可以使兩個子系統(tǒng)均經(jīng)歷圖靈分岔,從而各自激發(fā)相應的圖靈模式.由于圖靈模的波數(shù)與擴散系數(shù)成反比,所以具有較小擴散系數(shù)的子系統(tǒng)的圖靈模波數(shù)大(短波模),稱為 k2,本征值高度為 h2,而具有較大擴散系數(shù)的子系統(tǒng)的圖靈模波數(shù)較小(長波模),稱為 k1,相應的本征值高度為 h1.圖1(a)和圖1(b)給出了兩個圖靈模波數(shù)比分別為1∶2和1∶3時的色散關(guān)系圖.研究發(fā)現(xiàn),只有長波模 k1對短波模 k2有影響,而短波模 k2對長波模 k1沒有影響.因此長波模 k1一般設(shè)置為失穩(wěn)模.

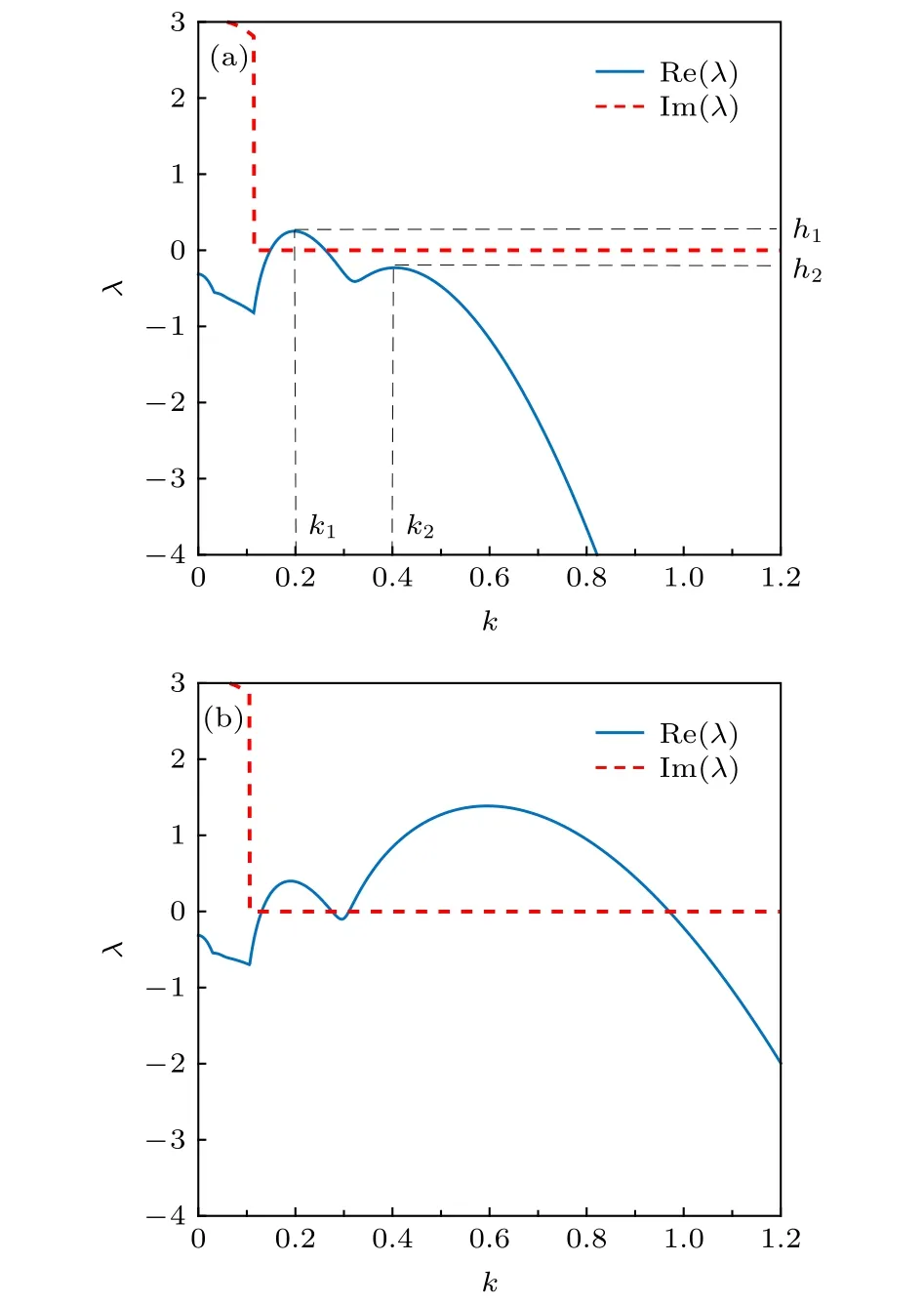
圖1 不同參數(shù)下耦合系統(tǒng)的色散關(guān)系 (a) Du1=12.6,Dv1=27.9,Du2=22,Dv2=420,α=0.1;(b) Du1=5.3,Dv1=20,Du2=22,Dv2=500,α=0.1Fig.1.Dispersion relations of coupled systems under different parameters:(a) Du1=12.6,Dv1=27.9,Du2=22,Dv2=420,α=0.1;(b) Du1=5.3,Dv1=20,Du2=22,Dv2=500,α=0.1.

3 模擬結(jié)果與討論

采用歐拉向前差分的方法進行積分,數(shù)值模擬在一個含有 1 28×128 個空間格點的二維平面上進行,時間積分步長取為 Δ t=0.01 個時間單位,空間積分步長取為 Δ h=1.0 個空間單位,擴散項在數(shù)值模擬中采取5點差分格式,邊界條件選用周期性邊界條件,初始條件為均勻定態(tài)加上一個很小的隨機擾動.如果沒有特殊說明,一般設(shè)置子系統(tǒng)2具有較大的擴散系數(shù),即激發(fā)長波模,而觀察子系統(tǒng)1中形成的各種斑圖.

接下來分別從波數(shù)比、相對強度以及耦合強度三個角度來討論兩個圖靈模之間的耦合作用以及相應的斑圖結(jié)構(gòu).

3.1 兩個圖靈模波數(shù)比的影響

固定兩個圖靈模的本征值高度(h1,h2)=(0.20,-0.55)以及耦合強度 α=0.1,通過改變兩個圖靈模的波數(shù)比值 K1:k2,研究不同波數(shù)比對斑圖形成的影響.如前文所述,圖靈模的波數(shù)大小取決于 Du和Dv的乘積,而其高度取決于 Du和Dv的相對大小,因此兩個圖靈模的波數(shù) k1和k2的大小可以通過其各自的 DuDv來控制.波數(shù)大小確定后,保持 DuDv的乘積不變,改變二者的相對大小,調(diào)節(jié)其本征值高度h.

圖2給出了波數(shù)比分別為1∶2,1∶3和1∶4三種比值下子系統(tǒng)1中形成的超點陣斑圖及其相應的傅里葉頻譜圖.圖2(a)是波數(shù)比為1∶2時得到的黑眼斑圖,其中每個中心點的濃度最低,且周圍環(huán)繞著一圈高濃度環(huán),整體呈現(xiàn)六邊形陣列排布.從其傅里葉頻譜圖可以看出,該黑眼斑圖包含三套不同波數(shù)的模式,其波數(shù)值分別為 k1,k2和q.每一套波矢都組成一個完美的六邊形結(jié)構(gòu),其中 k1和k2為兩個子系統(tǒng)激發(fā)的圖靈模 (K1:k2=1:2),而q是新生模式.這三種模式之間滿足空間三波共振關(guān)系:K1+k2=q.圖2(b)是波數(shù)比為1∶3時得到的白眼六邊形斑圖,與黑眼斑圖不同,白眼斑圖的中心為高濃度斑點,周圍依次圍繞一圈低濃度環(huán)和一圈高濃度環(huán),然后被6個更高濃度的亮點包圍,整體也呈現(xiàn)六邊形陣列結(jié)構(gòu).分析其傅里葉頻譜圖可知,該白眼斑圖同黑眼斑圖類似,也包含上述三套滿足空間共振關(guān)系的波矢,唯一的區(qū)別是新生模式q具有兩套六邊形結(jié)構(gòu),即12個波矢.通過幾何關(guān)系可知,此兩套六邊形之間的夾角為θ=21.8°.圖2(c)是波數(shù)比為1∶4時得到的白眼斑圖.與圖2(b)相比,每一個六邊形晶胞中心的亮斑點濃度下降,同時,晶胞外圍的六個亮點連接在一起,形成了一個蜂窩狀六邊形結(jié)構(gòu).它包含的波矢成分也較為復雜,除了基本的圖靈模 k1和k2外,還產(chǎn)生了各種高階模 2 k1,3 k1以及這些模式共振而生成的新生模式q.需要特殊說明的是,圖靈模式 k2的強度較弱,而高階模 3 k1的強度較強,這意味著當波數(shù)比較大時,子系統(tǒng)1中的斑圖主要是失穩(wěn)模 k1及其激發(fā)的高階模相互作用而形成.

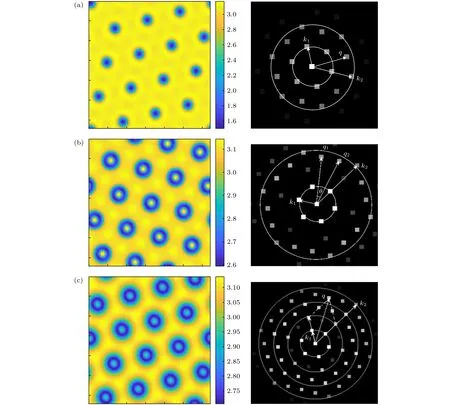
圖2 不同波數(shù)比下的超點陣斑圖及其傅里葉頻譜圖 (a) 1∶2下的黑眼斑圖,Du1=13.5,Dv1=27.5,Du2=22,Dv2=400 ;(b) 1∶3下的白眼斑圖,Du1=6,Dv1=12.3,Du2=22,Dv2=400 ;(c) 1∶4下的白眼斑圖,Du1=3.4,Dv1=6.96,Du2=21.9,Dv2=400.α=0.1Fig.2.Superlattice pattern and fourier spectrum under different wave number ratios:(a) Black eye pattern at 1∶2,Du1=13.5,Dv1=27.5,Du2=22,Dv2=400 ;(b) white eye pattern at 1∶3,Du1=6,Dv1=12.3,Du2=22,Dv2=400 ;(c) white eye pattern at 1∶4,Du1=3.4,Dv1=6.96,Du2=21.9,Dv2=400.α=0.1.

圖3給出了兩個圖靈模波數(shù)比為1∶5時所產(chǎn)生的振蕩超六邊形斑圖.圖3(a)為相應的色散關(guān)系曲線圖,由圖3(a)可知,在 k1和k2之間存在著一個虛部不為零的區(qū)域,即短波不穩(wěn)定性區(qū)域,在此區(qū)域內(nèi)的各個模式均隨時間周期性振蕩,失穩(wěn)模k1的高階模 2 k1和3 k1均位于此區(qū)域內(nèi).在此情況下,失穩(wěn)圖靈模 k1與其高階模 2 k1和3 k1相互作用時,就導致了一種正弦型時間振蕩斑圖的形成.圖3(b)給出了三個不同位置處(分別標記為A,B,C)活化子 u1隨時間變化的圖.其中B點為振蕩六邊形的中心斑點位置,其格點坐標為(50,76);A點為兩個中心亮斑的中心,其格點坐標為(53,59);C點為三個中心亮斑組成的三角形中心,其格點坐標為(65,61),如圖3(c)所示.由圖3(c)可知,三個位置處的振蕩周期相同,均為 T=t6-t1=46 個時間單位,但是相位不同,A,B,C相位依次延遲.另外,這三點的振蕩幅度也不相同,B點處振蕩幅度遠高于其他兩點.圖3(c)顯示了一個振蕩周期內(nèi)該振蕩六邊形斑圖的時空演化過程.在t1=24時刻,六邊形亮斑結(jié)構(gòu)濃度稍高于其它位置,從而形成了一種具有暈結(jié)構(gòu)的超六邊形斑圖.在t2=30時刻,中心斑點濃度下降,低于暈的濃度,此時斑圖呈現(xiàn)一種類似白眼斑圖的結(jié)構(gòu).在 t4=47 時刻,中心斑點處濃度降至最低點,遠遠低于暈的濃度,此時斑圖呈現(xiàn)為簡單的蜂窩六邊形斑圖.隨著時間演化,中心斑點處濃度開始上升,在 t6=64 時刻開始顯現(xiàn)出中心亮斑,有意思的是單元中心由原來的一個斑點變?yōu)閮蓚€斑點,并且每個單元外包圍著6個暗點.該時序振蕩六邊形斑圖與對稱耦合反應擴散模型獲得的眨眼斑圖[11]有著很大的區(qū)別.首先是形成機理不同,該振蕩六邊形是失穩(wěn)模與其高階模相互作用而成,而眨眼斑圖則是失穩(wěn)模與其次諧波模相互作用而成;其次是振蕩模式不同,該振蕩六邊形呈現(xiàn)正弦式的振蕩,而眨眼斑圖則呈現(xiàn)脈沖式的振蕩.

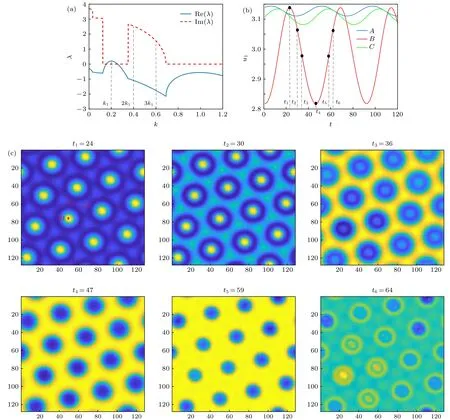
圖3 波數(shù)比為1∶5時的時間振蕩超六邊形斑圖,Du1=2.2,Dv1=4.5,Du2=21.9,Dv2=400,α=0.1 (a) 色散關(guān)系曲線;(b) 三個位置處u1的時間變化關(guān)系圖;(c) 一個振蕩周期內(nèi)的斑圖演化過程Fig.3.Oscillatory super-hexagon pattern with wave number ratio of 1∶5,Du1=2.2,Dv1=4.5,Du2=21.9,Dv2=400,α=0.1:(a) Dispersion curve;(b) time variation of u1 at three positions;(c) evolution of pattern in an oscillating period.

3.2 圖靈模強度對斑圖的影響

圖靈模的本征值高度h代表了圖靈模的線性增長率,h越大,表示增長率越快,意味著圖靈模強度越強.在本節(jié)中固定兩個圖靈模波數(shù)比為1∶3以及耦合強度 α=0.1,通過改變兩個圖靈模的本征值高度h來研究圖靈模強度對斑圖形成產(chǎn)生的影響.

首先固定本征值高度 h1=0.2,討論本征值高度 h2對圖靈斑圖的選擇及形成產(chǎn)生的影響.圖4給出了 h2逐步升高而獲得的各種復雜斑圖及其相應的傅里葉頻譜圖,其中圖4(a)—(d)是 h2＜0 的情況,圖4(e) 是 h2＞0 的情況.當 h2=-2.56 時系統(tǒng)1呈現(xiàn)簡單的蜂窩六邊形斑圖(圖4(a)).由于h2較低,該系統(tǒng)的本征模并不能被激發(fā),因此該六邊形斑圖完全是由系統(tǒng)2的失穩(wěn)模調(diào)制形成.隨著h2的升高,系統(tǒng)1中的本征模開始被激發(fā),如前文所述,兩個圖靈模相互耦合,形成了白眼斑圖(圖4(b)和圖4(c)).繼續(xù)升高 h2至—0.31,白眼斑圖失穩(wěn),轉(zhuǎn)變?yōu)橐环N新的超六邊形結(jié)構(gòu),該斑圖中每個晶胞均由三個相鄰的暗點排列而成,這些暗點的空間波數(shù)為 k2,晶胞之間以波數(shù) k1周期性排列(圖4(d)).當h2=0.67時,系統(tǒng)1呈現(xiàn)單一的條紋斑圖,也就是說此時系統(tǒng)1的斑圖完全由其自身的本征模所決定,系統(tǒng)2的長波模對它的調(diào)制作用僅僅存在于背景中,這可以通過傅里葉頻譜圖看出(圖4(e)).

另外h還表征了系統(tǒng)遠離初級分岔點的程度,h越大,偏離程度越高.早期的研究表明[13],在初級分岔點附近,系統(tǒng)一般選擇為六邊形斑圖,而當遠離分岔點時,選擇為條紋斑圖.因此通過改變h的大小還可以控制斑圖的對稱性類型.圖5給出了 h1分別為0.2和0.4兩種情況下子系統(tǒng)1中形成的復雜斑圖,這里固定兩個圖靈模的波數(shù)比為1∶3,h2=-0.5,耦合強度 α=0.1.當 h1=0.2 時,兩個子系統(tǒng)中的斑圖均為六邊形斑圖,對稱性相同,因此可以滿足空間共振關(guān)系,從而形成了白眼斑圖(圖5(a)).但是當 h1增大到0.4時,該失穩(wěn)模呈現(xiàn)出條紋結(jié)構(gòu),與另一個圖靈模的對稱性不匹配,不滿足空間共振關(guān)系,因此在子系統(tǒng)1中僅僅呈現(xiàn)簡單的重疊斑圖,即條紋結(jié)構(gòu)和六邊形的疊加(圖5(b)).

圖4 不同本征值 h 2 下的復雜斑圖及其傅里葉頻譜圖 (a) 蜂窩狀六邊形斑圖 h 2=-2.56,Du1=8.5,Dv1=12.5,Du2=22,Dv2=400 ;(b) 白眼斑圖 h 2=-1.3,Du1=7,Dv1=12.3,Du2=22,Dv2=400 ;(c) 白眼斑圖 h 2=-0.55,Du1=6,Dv1=12.3,Du2=22,Dv2=400 ;(d) 超六邊形斑圖 h 2=-0.31,Du1=5.9,Dv1=12.7,Du2=22,Dv2=400 ;(e) 條紋斑圖 h 2=0.67,Du1=5.5,Dv1=16,Du2=22,Dv2=400.α=0.1.Fig.4.Complex patterns and Fourier spectrum under different eigenvalues h2 :(a) Honeycomb hexagon pattern h 2=-2.56,Du1=8.5,Dv1=12.5,Du2=22,Dv2=400 ;(b) white-eye pattern h 2=-1.3,Du1=7,Dv1=12.3,Du2=22,Dv2=400;(c) white-eye pattern h 2=-0.55,Du1=6,Dv1=12.3,Du2=22,Dv2=400 ;(d) super-hexagon pattern h2=-0.31,Du1=5.9,Dv1=12.7,Du2=22,Dv2=400 ;(e) stripe pattern h 2=0.67,Du1=5.5,Dv1=16,Du2=22,Dv2=400.α=0.1.

詳細研究發(fā)現(xiàn),在該雙層耦合非對稱反應擴散系統(tǒng)中,兩個子系統(tǒng)要實現(xiàn)空間共振,其斑圖必須均為六邊形結(jié)構(gòu),即兩個模式的空間對稱性必須相同.對于失穩(wěn)模 k1,當本征值高度處于0＜h1＜0.33時,子系統(tǒng)自發(fā)選擇六邊形斑圖;當 h1＜0 時,系統(tǒng)是穩(wěn)定的,無法激發(fā)圖靈模;當 h1＞0.33 時,子系統(tǒng)選擇條紋斑圖.對于圖靈模 k2,其本征值高度范圍需在-2＜h2＜0 ;若 h2＞0 時轉(zhuǎn)變?yōu)槭Х€(wěn)模,此時子系統(tǒng)選擇條紋斑圖;而當其本征值高度過小時,盡管受到失穩(wěn)模 k1的激勵作用,但是依然無法激發(fā)出該本征模,此時子系統(tǒng)處于均勻定態(tài).

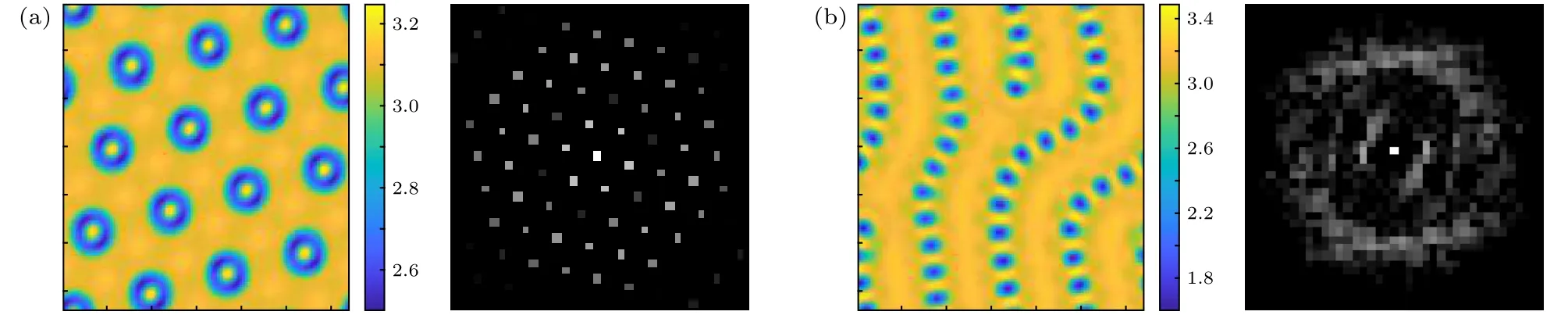
圖5 不同本征值 h1 下的復雜斑圖及其傅里葉頻譜圖 (a) 白眼斑圖,h 1=0.2,Du1=6.1,Dv1=12.7,Du2=22.3,Dv2=403;(b) 條紋點狀斑圖,h 1=0.4,Du1=6.1,Dv1=12.6,Du2=20.3,Dv2=464,α=0.1Fig.5.Complex patterns and fourier spectrum under different eigenvalues h1 :(a) White-eye pattern,h 1=0.2,Du1=6.1,Dv1=12.7,Du2=22.3,Dv2=403 ;(b) stripe-spot pattern,h 1=0.4,Du1=6.1,Dv1=12.6,Du2=20.3,Dv2=464,α=0.1.

圖6 不同耦合強度下的超六邊形斑圖 (a) 白眼斑圖,α=0.01,Du1=5.8,Dv1=11.4,Du2=22,Dv2=367 ;(b) 白眼斑 圖,α=0.1,Du1=6.3,Dv1=12.9,Du2=21.8,Dv2=395 ;(c) 新型超六邊形斑圖,α=0.2,Du1=6.1,Dv1=13,Du2=22,Dv2=432 ;(d) 新白眼斑圖,α=0.3,Du1=6.3,Dv1=13.98,Du2=22,Dv2=460Fig.6.Super-hexagon patterns with different coupling strength:(a) White-eye pattern,α=0.01,Du1=5.8,Dv1=11.4,Du2=22,Dv2=367 ;(b) white-eye pattern,α=0.1,Du1=6.3,Dv1=12.9,Du2=21.8,Dv2=395 ;(c) new superhexagon pattern,α=0.2,Du1=6.1,Dv1=13,Du2=22,Dv2=432 ;(d) new white-eye pattern,α=0.3,Du1=6.3,Dv1=13.98,Du2=22,Dv2=460.

3.3 耦合強度的影響

耦合強度也是影響兩個圖靈模相互作用的一個重要因素.由于各個參量共同影響兩個圖靈模的大小和強度,本文中改變耦合強度的同時對擴散系數(shù)進行微調(diào),以保證兩個圖靈模的大小 K1=0.2,k2=0.6和本征值高度 (h1,h2)=(0.2,-0.55) 始終保持恒定,從而研究耦合強度對斑圖形成的影響.圖6給出了不同耦合強度下獲得的超六邊形點陣斑圖.模擬研究發(fā)現(xiàn),耦合強度不僅可以影響斑圖的振幅大小,還影響了其空間結(jié)構(gòu)的具體形式.如果耦合系數(shù)足夠小,失穩(wěn)模對子系統(tǒng)1的影響可以忽略不計,此時子系統(tǒng)1呈現(xiàn)穩(wěn)定的均勻狀態(tài).當耦合系數(shù) α=0.01 時,子系統(tǒng)1開始受到失穩(wěn)模k1的調(diào)制和激發(fā),系統(tǒng)形成白眼斑圖,但是此時的活化子濃度的變化范圍非常小(圖6(a)).圖6(b)為耦合系數(shù) α=0.1 時模擬得到的白眼斑圖,從圖6(b)中可以看出,活化子濃度的變化范圍變大,圖靈模k2的強度也開始增強.繼續(xù)增大耦合強度α,子系統(tǒng)1中活化子濃度的變化范圍持續(xù)增加,并且其空間形貌逐漸開始變化.圖6(c)是模擬獲得的一種新型超六邊形斑圖,此超點陣斑圖雖然整體也呈現(xiàn)六邊形陣列結(jié)構(gòu),但是每一個晶胞單元中心不再是一個圓斑點,而是形成了一個線段,這可能是六邊形斑圖和條紋斑圖共同競爭的結(jié)果.圖6(d)給出了耦合強度 α=0.3 時得到的新白眼斑圖,與圖6(b)不同,此白眼斑圖在中心亮點周圍還包圍著一圈高濃度環(huán),環(huán)外排列著一組六邊形斑點.從傅里葉頻譜圖中可以看出,耦合強度很大,此斑圖也是由兩個圖靈模 k1和k2直接耦合而成.

4 結(jié) 論

通過線性耦合兩個不同的反應擴散模型(Brusselator模型和 Lengyel-Epstein模型)研究了不同系統(tǒng)間兩個圖靈模之間的相互作用以及斑圖的形成和選擇過程.模擬結(jié)果表明合適的波數(shù)比以及相同的對稱性是不同反應擴散系統(tǒng)的圖靈模之間相互共振的必要條件.只有長波模子系統(tǒng)對短波模子系統(tǒng)有調(diào)制和激發(fā)作用,因此超點陣斑圖只能出現(xiàn)在短波模子系統(tǒng)中.在不同的波數(shù)比下,短波模子系統(tǒng)內(nèi)可以形成包括黑眼斑圖和白眼斑圖在內(nèi)的多種超點陣斑圖.為了保證兩個子系統(tǒng)斑圖具有相同的對稱性,兩個圖靈模的本征值高度必須處于 0＜h1＜0.33和-2＜h2＜0.當失穩(wěn)模的高階諧波處于短波不穩(wěn)定區(qū)域時,失穩(wěn)模與其高階模相互共振可以形成一種正弦型時序振蕩六邊形斑圖.耦合強度直接影響了圖靈斑圖的振幅大小.本文的研究結(jié)果有助于人們進一步認知非線性系統(tǒng)中各種模式之間的相互作用機理.