“函數(shù)模型的應(yīng)用”教學(xué)設(shè)計(jì)及其評析

叢龍琦

一、教學(xué)內(nèi)容分析

本課選自人民教育出版社的A版高中數(shù)學(xué)必修1第四章第五節(jié)“函數(shù)模型的應(yīng)用”。本小節(jié)是函數(shù)的基礎(chǔ)知識和上一節(jié)“幾類不同增長的函數(shù)模型”的延續(xù)，在函數(shù)應(yīng)用（一）的基礎(chǔ)上，進(jìn)一步展開函數(shù)應(yīng)用。教材要求根據(jù)材料中提供的相關(guān)信息，分析和理解實(shí)際問題，對于已知函數(shù)模型能夠進(jìn)行應(yīng)用，對于簡單實(shí)際問題能夠自己建立函數(shù)模型并對其進(jìn)行求解、分析。本節(jié)課既是對前面所學(xué)函數(shù)基礎(chǔ)知識的總結(jié)，也開啟學(xué)生應(yīng)用函數(shù)的新世界。

二、學(xué)生學(xué)情分析

學(xué)生在本節(jié)課之前已經(jīng)掌握了一些基本初等函數(shù)的相關(guān)知識，結(jié)合實(shí)例學(xué)習(xí)了幾類函數(shù)的概念、圖像和性質(zhì)，并能應(yīng)用它們解決學(xué)科內(nèi)的一些問題和一些簡單的實(shí)際問題。但是面對較復(fù)雜的實(shí)際問題，不能將其轉(zhuǎn)化為數(shù)學(xué)問題，以及如何選擇函數(shù)模型來刻畫實(shí)際問題，大多數(shù)學(xué)生缺乏經(jīng)驗(yàn)，也缺乏數(shù)學(xué)抽象能力。

三、教學(xué)目標(biāo)確定

（1）根據(jù)表格提供的數(shù)據(jù)和已知馬爾薩斯人口增長模型，驗(yàn)證問題中數(shù)據(jù)與所提的數(shù)學(xué)模型是否吻合，培養(yǎng)數(shù)學(xué)抽象、數(shù)據(jù)分析和數(shù)學(xué)建模素養(yǎng);

（2）根據(jù)實(shí)際問題建立恰當(dāng)函數(shù)類型構(gòu)建函數(shù)模型，將實(shí)際問題劃歸為數(shù)學(xué)問題，通過運(yùn)算、推理求解函數(shù)模型，再將用數(shù)學(xué)知識和方法的得出的結(jié)論，還原到實(shí)際問題的解決，滲透應(yīng)用數(shù)學(xué)意識，使學(xué)生體會化歸思想，培養(yǎng)數(shù)學(xué)運(yùn)算能力;

（3）通過成功解決問題獲得學(xué)習(xí)成就感和樂趣，培養(yǎng)學(xué)習(xí)興趣。鍛煉克服困難的意志，建立學(xué)好數(shù)學(xué)的自信心。

四、教學(xué)重、難點(diǎn)

教學(xué)重點(diǎn)：歸納建立函數(shù)模型的基本過程

教學(xué)難點(diǎn)：對數(shù)據(jù)信息進(jìn)行擬合，建立函數(shù)模型，并進(jìn)行模型修正

五、教學(xué)方法

引導(dǎo)發(fā)現(xiàn)法：對生活中的實(shí)際問題進(jìn)行研究，引導(dǎo)學(xué)生對實(shí)際問題進(jìn)行數(shù)學(xué)抽象，對函數(shù)知識進(jìn)行應(yīng)用，并以多媒體課件及Excel計(jì)算為依托，增強(qiáng)課堂教學(xué)的直觀性、趣味性，促進(jìn)學(xué)生學(xué)習(xí)的積極性，引導(dǎo)學(xué)生思考、歸納、總結(jié)。

六、教學(xué)過程設(shè)計(jì)

【回顧舊知，創(chuàng)設(shè)情境】

復(fù)習(xí)回顧：到目前為止，我們已經(jīng)學(xué)習(xí)了

思考題：為什么我們要學(xué)習(xí)函數(shù)知識？

【設(shè)計(jì)意圖】通過貼近生活的問題背景，讓學(xué)生建立用恰當(dāng)函數(shù)模型解決問題，加深對函數(shù)概念本質(zhì)的認(rèn)識和理解，提升數(shù)學(xué)抽象核心素養(yǎng)。

函數(shù)與現(xiàn)實(shí)世界有著緊密的聯(lián)系，它是用來描述客觀世界變化規(guī)律的數(shù)學(xué)模型，面對實(shí)際問題時(shí)，該如何選擇恰當(dāng)?shù)暮瘮?shù)模型來刻畫它呢？

【講授新知，提煉方法】

知識探究：應(yīng)用已知函數(shù)模型解決實(shí)際問題

例題2 人口問題是當(dāng)今世界各國普遍關(guān)注的問題。認(rèn)識人口數(shù)量的變化規(guī)律，可以為制定一系列相關(guān)政策提供依據(jù)。早在1798年，英國經(jīng)濟(jì)學(xué)家馬爾薩斯就提出了自然狀態(tài)下的人口增長模型： （其中t表示經(jīng)過的時(shí)間， 表示t=0時(shí)的人口數(shù)，r表示人口的年平均增長率）

問題1：題中有哪些量是變量，哪些量是常量？

問題2：如果以各年人口增長率的平均值作為我國這一時(shí)期的人口增長率（精確到0.0001）， 的值為多少？

問題3：用馬爾薩斯人口增長模型建立我國在這一時(shí)期的具體人口增長模型。

問題4：檢驗(yàn)所得模型與實(shí)際人口數(shù)據(jù)是否相符。

問題5：如果按表4.5-4的增長趨勢，那么大約在哪一年我國的人口數(shù)達(dá)到13億？

求解得出我國1950-1959年期間人口增長模型為 （ ），畫出函數(shù)圖像，并根據(jù)表4.5-4中的數(shù)據(jù)畫出散點(diǎn)圖。由圖4.5-6可以看出，所得模型與1950-1959年的實(shí)際人口數(shù)據(jù)基本吻合。通過函數(shù)模型計(jì)算得出 ，即大約1950年后的第39年（1989年），我國人口會達(dá)到13億。而事實(shí)上我國直到2005年才突破13億，對由函數(shù)模型所得的結(jié)果與實(shí)際情況不符，你能找出原因嗎？

【設(shè)計(jì)意圖】：結(jié)合人口增長的實(shí)際社會意義和重要性激發(fā)學(xué)生的學(xué)習(xí)熱情和責(zé)任感;體會將實(shí)際問題轉(zhuǎn)化為數(shù)學(xué)問題并解決問題的過程。結(jié)合2005年1月6日我國人口達(dá)到13億的實(shí)際情況，探究數(shù)學(xué)模型失真的原因。

小結(jié)：用已知函數(shù)模型解題的一般過程：解模→建模→用模。

注意：由于實(shí)際問題的條件與得出已知模型的條件有所不同，往往需要對模型進(jìn)行修正。

【知識探究】：自己建立函數(shù)模型解決實(shí)際問題

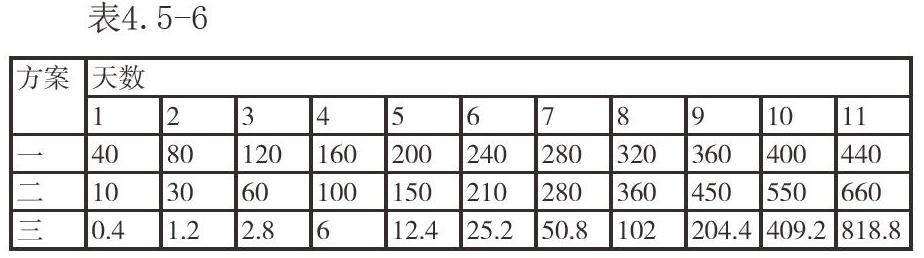
學(xué)生活動：完善累積匯報(bào)數(shù)，并通過計(jì)算器完成表4.5-6。

【設(shè)計(jì)意圖】：使學(xué)生注意實(shí)際問題中增長量和累積回報(bào)量的區(qū)別，應(yīng)用模型對實(shí)際問題進(jìn)行分析。

小結(jié)：自己建立函數(shù)模型解決實(shí)際問題一般程序是：審題--建模--解模--還原