趣說相交線與平行線

林革

提起相交線和平行線，相信大家早已屢見不鮮.

相交線和平行線在生活中的應用俯拾皆是、數不勝數.

我國北宋科學家沈括在其著作《夢溪筆談》中，記載了唐代著名科學家一行法師思考過的一個問題：圍棋棋局千變萬化，究竟有多少種變化呢？這得從圍棋盤的具體構造說起，圍棋盤上有互相平行的橫線19條，互相平行的縱線19條，橫線和縱線相交構成361個交叉點用于落子.一行法師認為：對于每一個交叉點，不外乎黑子、白子或空著三種可能情況，因此，361個交叉點就有3361種可能的變化，這是叫人嘆為觀止的天文數字，即便每一秒鐘下一棋子，不停地下，要完成如此多的變化，也大約需要5.52x10¹⁶⁴年.難怪有人感嘆：紋枰十九路，千古無重局，

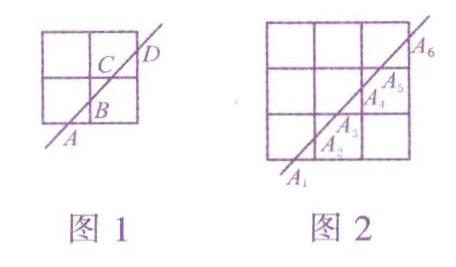
而下面這則“圍棋盤上的直線”趣題也很耐人尋味：相交的19條橫縱線把整個圍棋盤分成324個小方格，那么，在棋盤上任意畫一條直線，最多可以穿過多少個小方格？

要解答這個問題，許多人的直覺反應是實踐操作一一畫出圍棋盤，然后在上面畫直線，通過數數，得到穿過小方格的最多數目.這種想法看起來可行，可實際操作起來難免令人生疑：需要畫幾條直線才能保證穿過小方格數目最多的情形包含其中？如何確保最終確定的那條直線符合要求？即便是符合要求的直線，穿過的最多方格數也是操作的表面結果，其中蘊涵的數學原理是什么？因此，這種帶有隨機性的操作并不靠譜，而采用轉化策略則顯得科……