賴桂森 雷慶山 梁家豪 胡義 肖志超

（超高壓輸電公司廣州局 廣東省廣州市 510000）

1 問題描述

在大型高壓直流輸電系統中，高壓晶閘管換流閥是核心設備之一，晶閘管在工作時所產生的熱量，將會導致閥體溫度升高，當閥體溫度超過所允許的最高結溫時會導致器件性能惡化甚至損壞，因此必須配備相應的閥冷系統對器件進行散熱。目前在高壓直流輸電中基本采用水冷方式，保證換流閥的安全、穩定運行。

換流閥是直流輸電工程的核心設備，水冷系統是高壓直流輸電換流閥的必要輔助系統，是直流系統的重要環節和關鍵設備，充分實現換流閥在電流轉換過程中的有效散熱，保證換流閥的安全、穩定運行[1]。在水處理回路上設有氮氣穩壓系統，由氮氣瓶、氮氣管路、膨脹罐等組成。在膨脹罐的頂部充有穩定壓力的高純氮氣，以保持管路的壓力恒定和冷卻介質的充滿。膨脹罐可緩沖冷卻水因溫度變化而產生的體積變化。在水處理回路上設有氮氣穩壓系統，由氮氣瓶、氮氣管路、膨脹罐等組成。在膨脹罐的頂部充有穩定壓力的高純氮氣，以保持管路的壓力恒定和冷卻介質的充滿。膨脹罐可緩沖冷卻水因溫度變化而產生的體積變化[2]。

對于閥冷系統的膨脹罐，若能提前預測其排氣、補氣閥的工作狀態，將能有效提高控制質量和系統運行效率，降低工程成本。閥門的工作狀態取決于膨脹罐內冷卻水的壓力，通過設置壓力定值作為閥門工作與停止的條件以進行控制[3]。因此，對將來壓力進行直接或間接的建模預測對閥冷系統的改進有著重要的意義。目前，預測模型的應用與成果頗豐。王永生等人將最小二乘支持向量回歸用于預測研究，降低了計算復雜程度和提高了建模訓練速度[4]。馬仕強等人將粒子群算法運用到模型參數自動尋優，提高了模型預測能力[5]。盧曉航等人構建了滑動窗口模型，進行學習者輟學率的動態跟蹤預測[6]。針對短時交通流的預測，唐智慧等人提出基于交互式模型的短時交通流預測方法[7]，孫靜怡等人提出了考慮大型車因素的支持向量機短時交通狀態預測模型[8]。

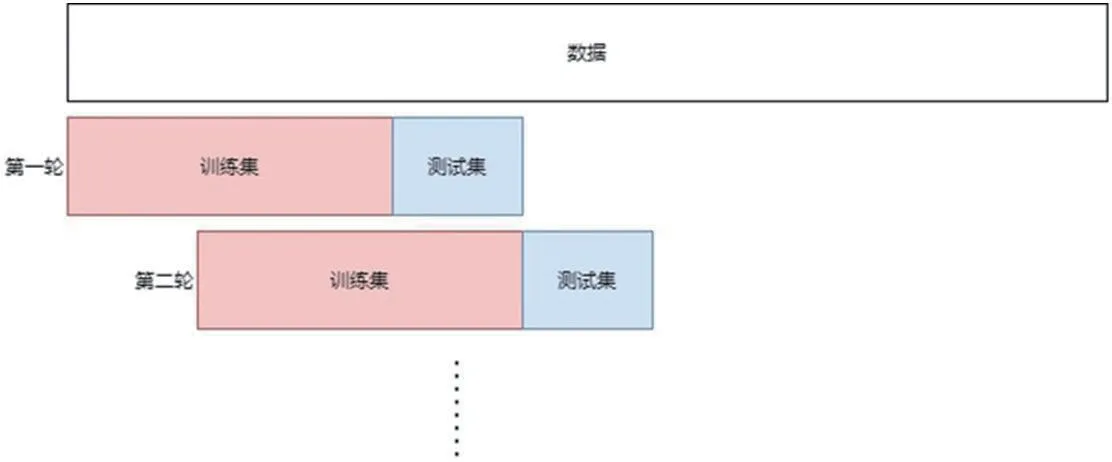
圖1：滑動窗口結構

在±800kV 換流站直流運行狀態下，本文建立滑動窗口的最小二乘支持向量回歸閥冷系統膨脹罐閥門壓力預測模型，通過滾動窗口對模型進行動態更新；最后，對于基于實際數據建立的模型進行驗證。

2 滑動窗口的最小二乘支持向量回歸算法

最小二乘支持向量機（Least Squares Support Vector Machine,LSSVM），采用最小二乘線性系統作為損失函數，在其優化問題的目標函數中使用二范數，并利用等式約束條件代替支持向量機標準算法中的不等式約束條件，使得LS-SVM 方法的優化問題的求解變為線性方程組的求解，避免了二次規劃問題，具有更快的求解速度和更小的計算復雜性，能夠以自回歸的形式來處理動態問題，對于在線計算方面應用廣泛。

最小二乘支持向量回歸是用一個超平面對已知數據進行擬合，可分為線性回歸和非線性回歸，在實際應用過程中，大部分問題都不是線性的，若采用線性回歸方法往往是難以達到精度要求，因此大多數情況下都會使用非線性回歸進行求解，其回歸方程如下：

同時，為了解決存在部分特異點的情況，給每一個樣本引入誤差變量ek，并在原始函數中加入誤差變量的L2 正則項，則約束問題為：

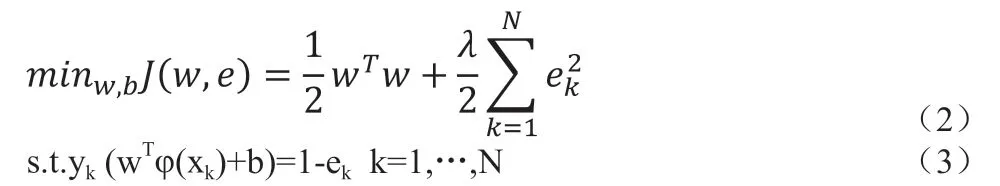
式中，λ 為正則化系數，φ(xk)將xk映射到更高維的空間。

采用拉格朗日乘數法：

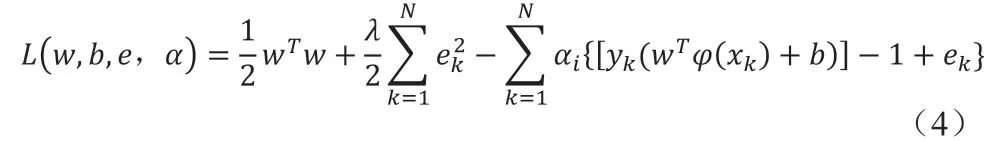
最后將約束問題轉換為解線性方程組：

式中，K 為核矩陣，矩陣中各個元素Kij=k(xi,xj)，k(xi,xj)為核函數，通過核函數的映射，我們將高維空間的內積運算轉化為低維空間的核函數計算，避免了“維數災難”。

本文將采用此最小二乘支持向量回歸方法，且在此法中加入滑動窗口技術，進行基于滑動窗口的最小二乘支持向量回歸的建模。滑動窗口技術（Siding Window algorithm），本文將使用此法進行數據集的劃分。首先定義窗口尺寸，按照從前往后的順序移動窗口，窗口內的數據將作為訓練集進行建模訓練，并以此模型進行數據預測，得到預測結果，然后再將窗口移動到下一位置重復進行上述步驟。其主體思想可表述為如圖1所示。本文共有數據358 點，設置窗口尺寸為158，測試集大小為20。

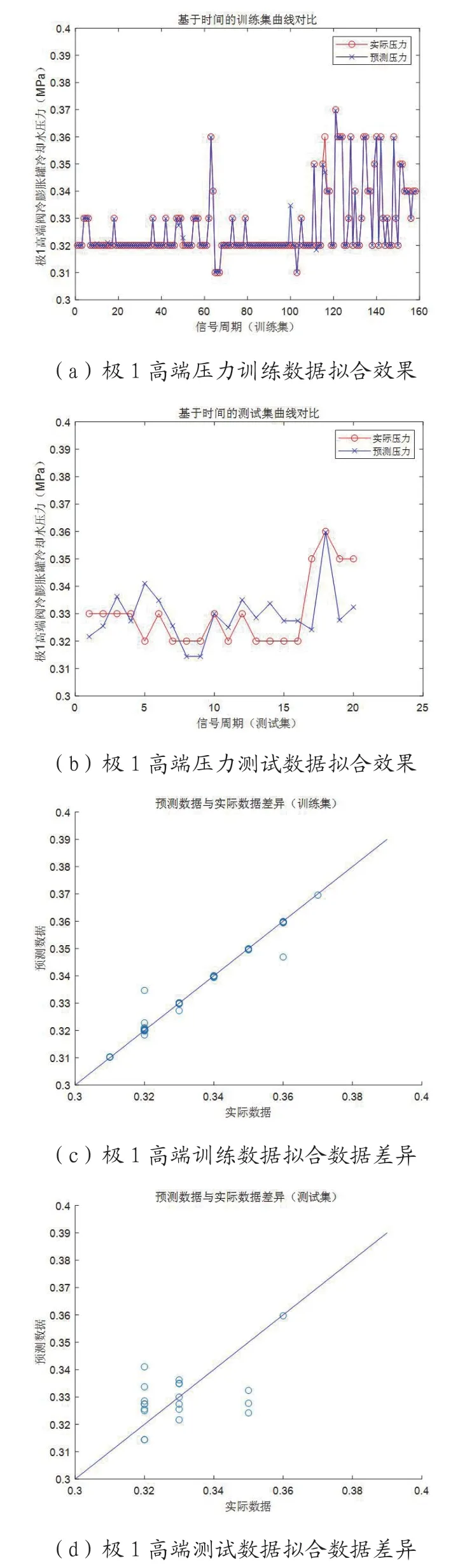
圖2：極1 高端壓力預測模型測試

3 閥冷系統壓力的滑動窗口LS-SVM預測建模與分析

在閥冷系統中，補氣閥和排氣閥的工作狀態直接由閥冷膨脹罐冷卻水壓力決定，因此以壓力直接作為模型輸出。本文首先選擇環境溫度、冷水進閥溫度、冷水出閥溫度、功率作為模型輸入，這4個參數會直接或間接地影響冷卻水壓力，然后通過滑動窗口建立模型進行測試集的預測，以每158 點的訓練集所得到的模型來預測接下來20 點的壓力，由于原數據共有358 點。因此，需進行10 輪的建模與預測。除曲線擬合對比外，還制作了橫坐標為實際數據、縱坐標為預測數據的坐標圖，以45°直線為分界線，位于直線上的點為預測數據與實際數據相同的點，并對每輪的均方誤差進行求和取平均，作為模型預測效果的評價之一。

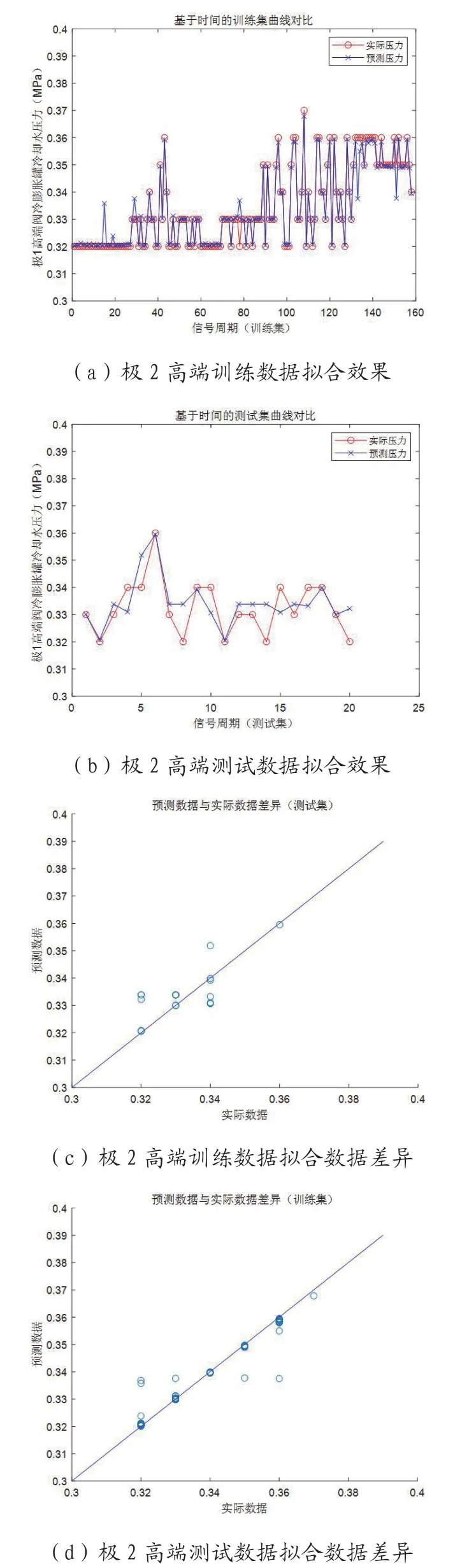
圖3：極2 高端壓力預測模型測試

在極1 高端情況下，我們建立閥冷系統壓力的滑動窗口LSSVM 預測模型，并進行數據擬合。極1 高端壓力預測模型測試如圖2所示。結果表明，所建立的模型能夠對閥冷系統壓力進行有效預測。經計算，訓練集的均方誤差為3.9703×10-6，測試集的均方誤差為1.7866×10-4。

進而，在極2 高端情況下，我們建立閥冷系統壓力的滑動窗口LS-SVM預測模型，并進行數據擬合。極2 高端壓力預測模型測試如圖3所示。結果表明，所建立的模型能夠對閥冷系統壓力進行有效預測，預測數據和實際數據能夠較好地擬合，訓練集、測試集的均方誤差分別為4.2114×10-6與2.0519×10-4。

綜上可以看出，本文以環境溫度、冷水進閥溫度、冷水出閥溫度、功率作為模型輸入，以膨脹罐壓力為輸出，建立的模型能夠獲得較好的預測效果，預測數據與實際數據差異較小，擬合程度較高，表明了該模型是有效的。實際工程應用中，可以基于該模型對壓力進行預測，對于可能發生的補、排氣進行預測，提前進行運行規劃，提高現場管理效率。

4 結束語

本文引入實測東方換流站閥冷系統數據，選擇環境溫度、冷水進閥溫度、冷水出閥溫度、功率作為模型輸入，對膨脹罐冷卻水壓力建立了預測模型，所建立的模型基于最小二乘支持向量回歸方法，采用了滑動窗口技術進行模型大小的優化，通過數據仿真驗證了所提出方案的有效性。本文結果對閥冷系統膨脹罐閥門的未來工作狀態進行預測，指導合理及時地補充氮氣，對閥冷系統正常運行及改進方向具有一定的參考意義。