基于FPGA的查表式運算器的設計

金天星 閔嘯

（中國船舶重工集團公司第七二三研究所 江蘇省揚州市 225011）

電子計算器已經變成現代人生活中不可缺少的工具，給人們的工作和生活帶來諸多便利。隨著人們對計算功能的要求越來越高，各種新型的技術也逐漸運用到計算器運算領域，當前，基于FPGA的運算系統應用較為廣泛，在傳統的運算技術上進行了優化，其計算時間更快，并且能處理更大量級的運算，它不僅給人們帶來了很大的便利，還為現代人提供了更迅捷的計算速度，具有非常強大的運算功能。

1 計算器運算系統的總體設計

系統總體設計框圖如圖1所示。此設計由計算部分、存儲部分、顯示部分和輸入部分組成。

1.1 計算器的計算部分

首先，該系統計算部分所采用是8 位或4 位二進制的計算方式，這也是目前應用較為廣泛的一種計算方式，其計算語言為VHDl 語言，通過VHDl 語言中的運算符就能將各個數字之間的運算銜接起來。然而，在計算器的顯示過程中，百位、十位、個位等必須都是分開顯示的，這就需要用到比較的方法去實現。當然，采用VHDl語言進行計算時只能處理以2 位除數的冪的除法，而不能處理除數是其它數字的運算，此時就要求另外設計一個除法器來完成除法運算，這個除法器所采用的是左移運算和減法運算等程序。

1.2 計算器的存儲部分

我們都知道計算器的存儲部分是非常的重要的，它主要有三個存儲器去實現它的計算的功能，包括：結果暫存器（ans）、輸入寄存器（reg）和內部累加器（acc）等。通常，將輸在存放在輸入寄存器或內部累加器中，第一次按下數字按鍵就能直接顯示個位，第二次按下數字按鍵時就表示此時輸入的是個位，而上一次輸入的十位，因此，第一次輸入的數字就必須乘以10，并與第二次輸入的數字進行相加，得到的就是計算結果。同理，第三次按下數字按鍵時，就要將第一次輸入的數字要乘以100，并與第二次輸入的數字乘以10 以及第一次輸入的數字進行相加，得到最后的計算結果。

1.3 計算器的顯示部分

我們都知道計算出來的結果，一定要顯示在屏幕上，我們用的屏幕是Fede 的屏幕，這種屏幕功能是非常的強大的，能夠更好的顯示圖形和數字符號。該運算系統采用的是二進制運算方式，用BCD 碼來詮釋輸出表達方式，因此，可以在FPGA 中運用譯碼程序來實現。該系統選用共陽極七段譯碼管，當需要顯示數字時對應的管腳將切換到低電平，在輸出的過程中，按照從左到右、從高到低的順序，依次為g、f、e、d、c、b、a，其結構圖如圖2。

通過查閱大量的數據我們編寫出相關的代碼，并且能夠更好的去實現功能。為了設計出計算器中的顯示功能，所采用的的七段譯碼器，同時運用3 個七段譯碼器，依次顯示出百位、十位、個位。當把第1 個數字輸進去后，在按下第2 個數字之前，此時三個七段譯碼器都直接將第1 個數字顯示出來。當輸入完第2 個數字后，則會直接將第2 個數字顯示出，然后，在按下第3 個數字之前，直接將前面兩個數字的運算結果顯示出來，以此類推，最后按下等號鍵，其最終的運算結果就快速顯示。

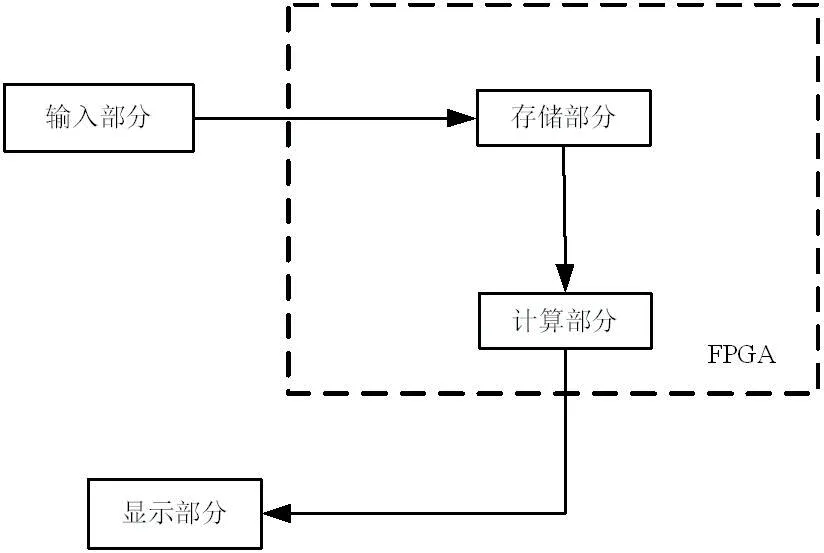
圖1：計算器的系統組成框圖

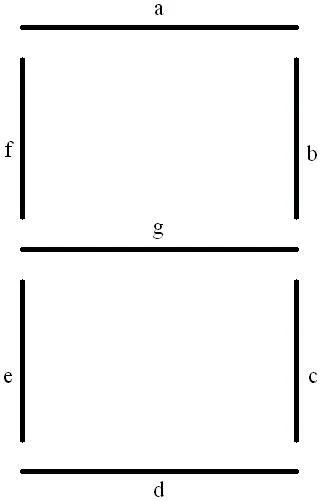
圖2：七段譯碼器的結構

1.4 計算器的輸入部分

在生活中接觸計算器的次數較多，都知道計算器上的數字的一般都是都是10 個數字，通過這十個數字不斷的加減乘除，都可以計算出想要的結果，并顯示到計算器的顯示屏上。

在這次設計中，程序是非常的重要的，而設計科學的、合理的按鍵譯碼電路是計算器輸入部分的關鍵流程。其中，計算器的輸入部分包括0-9 等10 個數字符號、加減乘除等4 個運算符號、1 個清零鍵、1 個等號鍵等。因此，就要求對每個按鍵進行不同譯碼，保證按鍵數字的準確性。

圖3：加法器仿真16+176=192

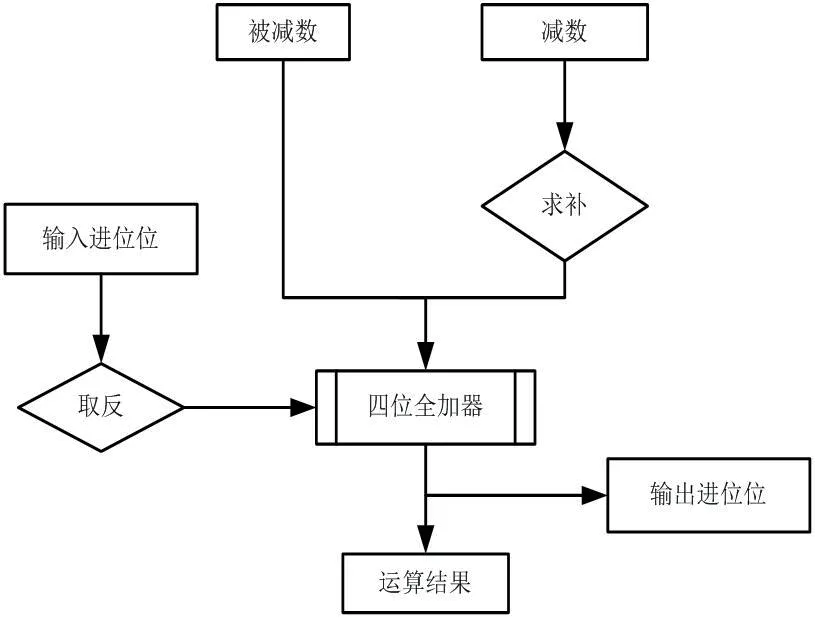
圖4：四位全減器的原理框圖

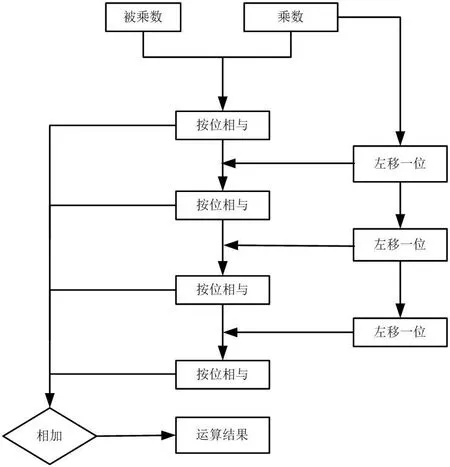
圖5：乘法器的原理框圖

2 計算器的VHDL設計

2.1 加法器的設計

本文設計的加法器運算程序是多位加法器，能夠根據不同的進位方式劃分成兩種類型，即并行進位加法器和串行進位加法器。其中，串行進位加法器運行原理為把多個一位全加器級聯，低位全加器的進位輸出送給相鄰高位全加器作為進位輸入。顯而易見，該設計方式所需要的資源更少，并且思路非常簡明，然而運算的速度并不快。并行進位方式的運行原理為基于各位的加法程序的基礎上，添加進位發生的邏輯電路，各位的進位輸入信號都是同時出現，這就可以保證各位能一起進行全加加算，并顯示出計算結果。這種運算方式需要的資源較多，運算速度是非常快的。特別在處理運算位數增加的過程中，相比于串行進位加法器，并行進位加法器占用的資源更大。所以，在設計加法器時，必要要全面對比資源占用量和運算速度，盡可能地實現設計平衡。根據相關資料可知，在采用4位二進制的方式進行運算時，二者資源占用量基本一致。所以，就能夠將兩個4 位二進制并行加法器級聯從而從此一個8 位二進制加法器。

接下來，需要去詳細的分析這個程序的運行過程，并通過仿真評定其準確性和合理性。加數和被加數進行相加，并且個位和十位、百位都是相對應的，相加之后進行四舍五入的方法總結出來的結果，并且把結果顯示到屏幕上去，這樣更加的直觀而和真實的地了解加法的計算結果。如圖3所示，能夠更好的讓我們分析十六進制和八進制的區別，能輕易分辨出二者是如何進行運算的，通過這種形式能夠讓我們通過仿真的方式進行分析和驗證，最重要的是可以得出正確的仿真結果，也就表明設計出的加法運算器非常的成功。

2.2 減法器的設計

上文我們已經介紹了加法的運算器的運行的原理。接下來我們就介紹減法的運算器的原理，其實加法的運算器的原理和減法運算器的原理都是相通的，它們都是一樣的，都是通過數字與數字進行相減，個位和個位相減、十位和十位相減、千位和千位相減，直接將運算的結果顯示出來，具體的流程圖、原理圖，如圖4所示。

2.3 乘法器的設計

乘法的運算器是非常難以解決的，所需要的步驟也是非常多的，通過移位的方式去實現相關的運算。在數字系統中，乘法器屬于基本的邏輯器件，并且在應用過程中會發生不同類型的濾波器的設計、矩陣的運算等。本文所設計的乘法器程序是4×4，最終得出了乘法運算器的原理的框圖如5 所示。

2.4 除法器的設計與仿真

除法運算器實在移位和連減的基礎上完成的，而連減實際上也是基于數學上除法的基本原理。由于運算方式采用的是二進制，就能夠進行移位操作。該計算器所采用的除法器運用了一個可以控制移位的控制器，再加上由全加器組成的4 位減法器。當做完減法，需要再次判斷是否夠減，也就是判斷有沒有發生錯位，如果不夠減，需要將被減數進行恢復，移一位再減。

3 總結

本次研究是采用FPGA（現場可編程邏輯器件）來設計查表式運算器的，所采用的的語言包括VHDL，并進行編程程序，最后也運用Quartus Ⅱ軟件進行仿真。雖然運算器的功能不強，只是簡單的運算功能，但采用諸多編程技術，經過經過外接鍵盤輸入、LED數碼顯示來達到和完成運算目標。