同方向同頻率簡諧振動合成問題求解方法的研究

賈冬梅

（中北大學信息商務學院 山西省晉中市 030600）

簡諧振動是機械振動中最簡單、最基本的振動形式，任何復雜的振動都可以看作是簡諧振動的合成[1]。而同方向同頻率的簡諧振動的合成又是簡諧振動的合成中最簡單最重要的形式，它為波干涉和衍射現象的分析奠定了理論基礎，因此研究同方向同頻率簡諧振動的合成有著十分重要的意義。尋求一種高效便捷的求解簡諧振動合振動的振動的方法成為了解決同方向同頻率簡諧振動的合成的關鍵[2-4]。對于同方向同頻率簡諧振動的合成問題，大學物理教材中常使用旋轉矢量法和解析法來進行討論分析[5-6]。下面分別運用解析法和旋轉矢量法來求解同方向同頻率簡諧振動合成問題，分析總結它們各自的特點，為這類問題的分析和求解提供一些參考和借鑒。

1 兩個同方向同頻率簡諧振動的合成

設兩個簡諧振動都沿著x 軸方向振動，平衡位置都為坐標原點，它們振動的角頻率ω，振幅分別為A1和A2，初相分別為φ1和φ2，它們的振動方程分別為：

x1=A1cos(ωt+φ1)

x2=A2cos(ωt+φ2)

求這兩個解析振動的合振動。

1.1 解析法

由于兩個簡諧振動都沿著x 軸方向振動，所以這兩個簡諧振動在任一時刻合振動的位移也應在x 軸方向上，且合振動的位移x 等于這兩個分振動位移的代數和，即：x=x1+x2

將分振動的方程x1和x2代入上式展開整理：

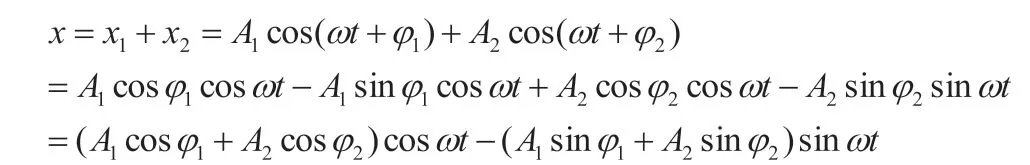
令A cosφ=A1cosφ1+A2cosφ2A sinφ=A1sinφ1+A2sinφ2

得到x=A cosφ cosωt-A sinφ sinωt=A cos(ωt+φ)

這一結果表明：兩個同方向同頻率簡諧振動的合振動依舊是一個簡諧振動，且合振動的頻率與分振動的頻率相同都等于ω，合振動的振幅和初相可以表示為：

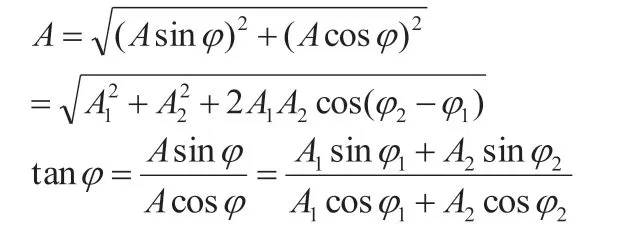
1.2 旋轉矢量法

如圖1所示，和 分別為兩個分振動的旋轉矢量，它們以相同的角速度繞o 點做逆時針轉動，t=0s 時它們與x 軸正向的夾角分別為φ1和φ2。根據平行四邊形法則，兩個簡諧振動旋轉矢量的合矢量為。由于旋轉矢量的大小不變，且以相同的角速度ω 繞O 點做逆時針旋轉，它們的夾角在旋轉過程中也保持不變，所以合矢量在旋轉的過程中大小也保持不變，并以相同的角速度ω 繞O 點做逆時針旋轉，說明合矢量在坐標軸上的投影仍為簡諧振動。設任一時刻和在x 軸上的投影分別為x1和x2，合矢量在x 軸上的投影為x，由圖中幾何關系可以得出x=x1+x2，故合矢量即為合振動所對應的旋轉矢量，合振動的運動方程為：x=A cos(ωt+φ)量與ox軸的夾角為合振動的初相。通過圖中旋轉矢量的幾何關系也可以得出合振動的振幅和初相的表達式分別為：

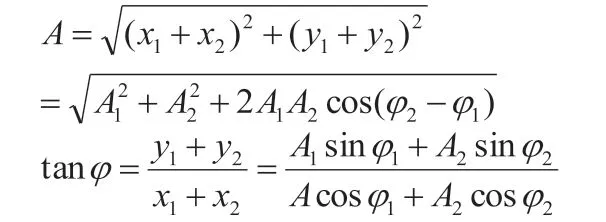
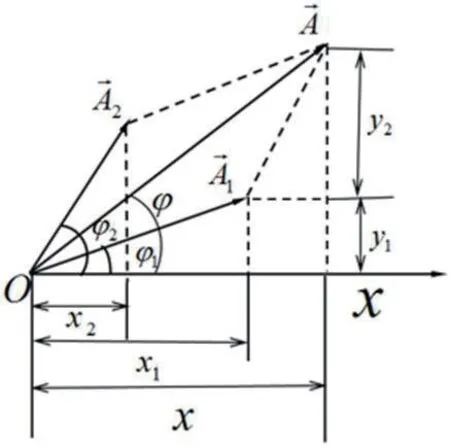
圖1：旋轉矢量示意圖

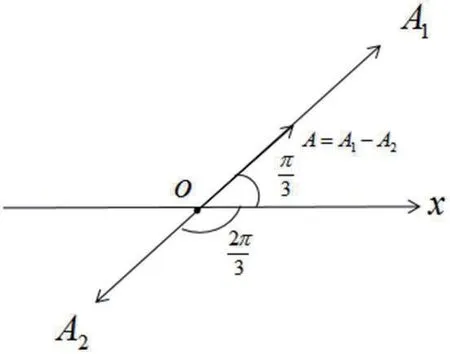
圖2：例1 旋轉矢量圖

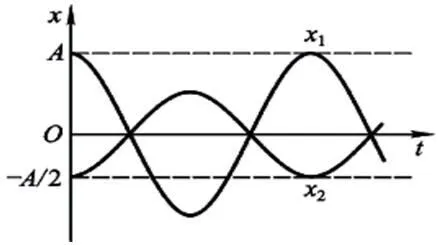
圖3：簡諧振動曲線

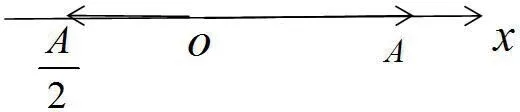
圖4：例2 旋轉矢量圖

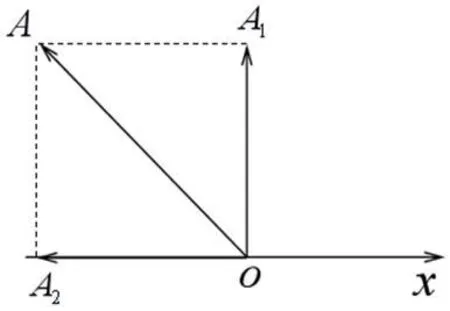
圖5：例3 旋轉矢量圖

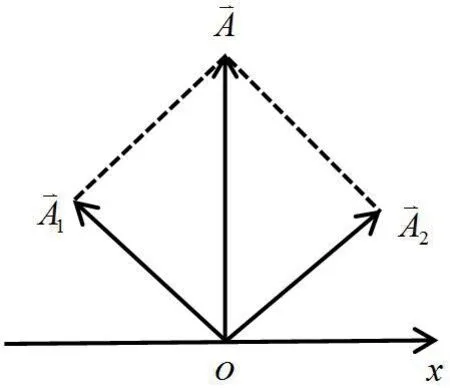
圖6：例4 旋轉矢量圖

運用解析法和旋轉矢量法分析兩個同方向同頻率簡諧振動合振動得到了完全相同的結果。其中，解析法是運用三角函數關系化簡整理得到合振動的振動方程及合振動與分振動之間的數學關系。旋轉矢量法是通過畫旋轉矢量圖來分析合振動的振動特征，并且從旋轉矢量圖中可以直觀地給出合振動與分振動之間的數學關系。

2 同方向同頻率簡諧振動合成問題解析

例1 兩個同方向、同頻率的簡諧振動，其振動表達式分別為：

求它們的合振動的振幅和初相。

解法一（解析法）。

解：由已知條件得：

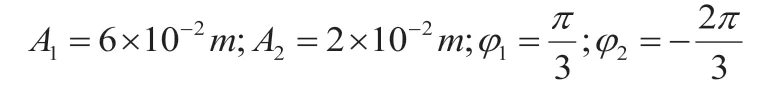
將其代入合振動的振幅公式得：

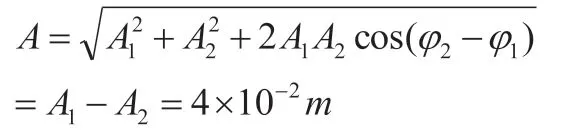
解法二（旋轉矢量法）

解：根據已知條件得知初始時刻兩個簡諧振動的旋轉矢量圖，從圖中可以看出振動的振幅為：

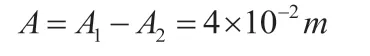
2.1 求合振動的初相位

例2 如圖3所示是兩個簡諧振動的曲線，若這兩個簡諧運動可疊加，則合成的余弦振動的初相位為？[6]

解法一（解析法）

解：由簡諧振動的運動曲線得：

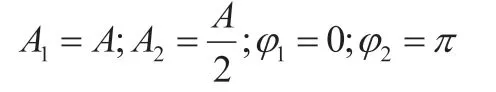
將其代入合振動相位公式得：

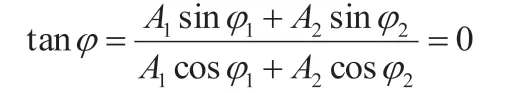
故合振動的初相為：φ=0

解法二（旋轉矢量法）

解：根據簡諧振動的振動曲線畫出它們初始時刻的旋轉矢量圖如圖4所示。t=0s 時，疊加后簡諧振動的旋轉矢量沿著x 軸的正方向，與軸的夾角為零，故合振動的初相φ=0。

2.2 求合振動的振動方程

例3：兩個同方向、同頻率的，其振動表達式分別為：

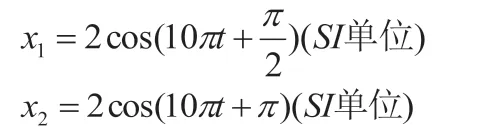
求其合振動的振動方程。[5]

解法一（解析法）

最后，小編還是要提醒一下，食品藥監總局給予貝因美愛加幼兒配方奶粉“0001號”的殊榮和肯定，再加上價格定位都在300元左右主流價格帶，相信在高品質的保證下，以這個價位，未來母嬰店選擇貝因美愛加定能取得不錯的銷售成績。

解：兩個同方向同頻率簡諧振動的合振動依舊是簡諧振動，故設合振動的振動方程為：

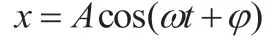
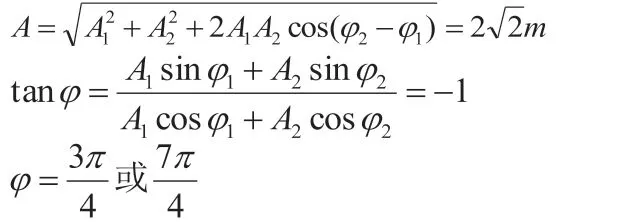
合振動的振動方程為：

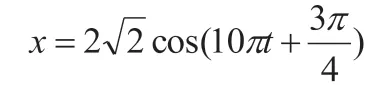
解法二（旋轉矢量法）

解：根據已知條件得知初始時刻兩個簡諧振動所對應的旋轉矢量如圖5所示。由圖中幾何關系可得合振動的振幅和初相分別為：

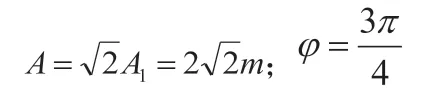
例4 已知兩同方向、同頻率的簡諧運動的運動方程分別為：

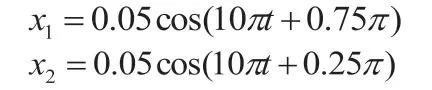
求：（1）合振動的振幅及初相；（2）若另有一個同方向同頻率的簡諧振動則φ3為多少時x1+x2+x3的合振動振幅最大？為多少時x1+x2+x3的合振動振幅最小？

解法一（解析法）

解：（1）由已知條件得：

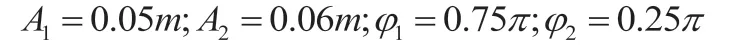
解法二（旋轉矢量法）

解：（1） 作兩個簡諧運動合成的旋轉矢量圖如圖6所示。

故簡諧振動合振動振幅為：

（2）由簡諧振動合成的旋轉矢量圖可以看出，要使的振幅最大，簡諧振動x3的旋轉矢量應與簡諧振動的x1，x2合振動的旋轉矢量同，故：要使的振幅最小，簡諧振動x3的旋轉矢量應與簡諧振動的x1，x2合振動的旋轉矢量反相，故：

通過對以上例題的分析可以看出：在一些特殊情形下，即當兩個分振動的的相位差為時，運用解析法和運用旋轉矢量法求合振動的振幅是等效的，但是運用解析法需要理解記憶合振動的振幅公式，而運用旋轉矢量法則不需要記公式，只需要畫出兩個分振動的旋轉矢量圖，就可看出合振動的振幅與兩個分振動振幅之間的數學關系。特別是對于合振動初相位的確定，運用旋轉矢量法比解析法更為直觀、便捷和有效。但對于一般情形下同方向同頻簡諧振動的合成，運用解析法來求合振動更為有效。

3 結論

運用解析法和旋轉矢量法分別從代數和幾何的角度來分析同方向同頻率簡諧振動合成，并得到完全相同的結。比起解析法復雜數學計算過程，旋轉矢量法這種簡單的幾何圖形的方法更加直觀、便捷。因此，在教學過程中，教師在講解同方向同頻率簡諧振動的合成時，運用旋轉矢量法來分析比用解析法分析更加便于學生的理解和掌握。

對于同方向同頻率的簡諧振動合成問題的求解，運用解析法所使用的數學過程和函數圖像知識比較復雜，計算難度較大，而且還需要理解和記憶相關物理公式，這些都使得學生掌握簡諧振動的合成問題難度增大。而運用旋轉矢量法可以避免學生對物理公式的記憶和復雜的數學計算,特別是對于合振動初相的確定，旋轉矢量法更加直觀、有效和便捷。