基于二維串聯調制耦合映射的圖像加密-秘密分享算法

王宛平,李 冰

(1.河南質量工程職業學院現教中心，河南 平頂山 467000；2.平頂山學院,河南 平頂山 467000)

1 引 言

隨著多媒體技術及因特網的發展，數字圖像在互聯網中的收發越來越頻繁，其存儲總量也越來越多[1-2]。近年來，一些針對數據云中心的網絡攻擊造成了一系列嚴重的損失，因此高價值數字圖像在數據云中心的安全存儲問題引發了廣泛關注。針對這一問題，研究者們提出了一系列的解決方案。在圖像抗破譯方面，研究者們提出了圖像加密[3-4]、圖像隱寫[5-6]等技術。在圖像的抗破壞方面，研究者們提出了圖像分布式存儲[7]，圖像秘密共享[8-9]等技術。

由于混沌映射對初始迭代值及系統參數的高度敏感性與圖像加密算法所要求的高度密鑰敏感性不謀而合，因此各種基于混沌映射的圖像加密算法在實際中應用最為廣泛。在現實場景中，為了避免存儲設備的偶發故障而導致的圖像數據丟失，圖像的分布式備份存儲是一種常用的手段。但這種冗余手段也會增加圖像被竊取、篡改的風險。有鑒于此，部分研究者提出了(k,n)門限圖像秘密分享技術，將圖片通過秘密分享技術拆分成n份，任意k份便可以完整恢復出原始圖像，但少于k份則不能得到任何原始圖像中的有用信息。這種特性完美地解決了圖像分布式存儲的安全問題，因此得到了廣泛應用。

為同時提高圖像的抗破譯能力和抗破壞能力，本文設計了一種新型的圖像加密-秘密分享算法，在算法中，基于2D-CMCM的圖像加密算法和基于拉格朗日插值的(k,n)門限秘密分享算法被合并使用，同時，在圖像加密環節，本文通過已加密像素點參與加密新像素點的方式使算法具有了明文相關特性，這種特性進一步提升了算法的安全性。在安全性分析中，本文所提出算法顯示出了高度的抗攻擊性；在可逆性分析中，通過秘密分享產生的秘密子圖被證實可以實現原始圖像的無損重構；在執行效率測試實驗中，本文所提出的算法的高執行效率也得到了驗證。經過一系列實驗，本文所提出算法的高度實用性得到了證實。

2 理論基礎

2.1 2D-CMCM

文獻[10]通過合并混沌映射串聯架構[11]和混沌映射閉環耦合架構[12]，提出了一種新型的串聯調制耦合架構(Cascade modulation couple module,CMC)。該架構如公式(1)所示。

(1)

其中:f為一個線性映射函數，G,F分別為一個一維混沌映射。序列X={xi,i=0,1,2,…}和序列Y={yi,i=0,1,2,…}為該混沌映射架構所生成的兩個混沌序列。k∈(0,+)為調制耦合參數。在該架構中，映射G的輸出通過線性函數f進行調制，調制之后的輸出作為混沌映射F的輸入，其在各個階段的輸出構成混沌隨機數序列。

Logistic映射[13]和無限折疊迭代混沌映射[14](Iterative chaotic map with infinite collapse,ICMIC)因優良的混沌性能，在密碼學的各項應用中被廣泛采用。這兩個一維混沌映射的數學定義如公式(2)和(3)所示。

xi+1=αxi(1-xi)，

(2)

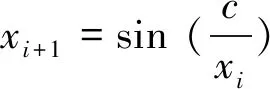
(3)

其中：α和c均為系統參數。當滿足α∈(0,4]時Logistic映射處于混沌狀態，當滿足c∈(0,+)時ICMIC處于混沌狀態。在文獻[10]中，線性映射函數被定義為f(x)=x+3，混沌映射G、F分別被定義為Logistic映射和ICMIC。其中ICMIC的系統參數c=21。通過此種方式設定的混沌映射被稱為二維串聯調制耦合映射(Two-dimensional cascade modulation coupling map,2D-CMCM)，如公式(4)所示。

(4)

2.2 (k,n)門限秘密分享

設待處理的密鑰數據為D，Shamir[9]提出的(k,n)門限密鑰秘密分享方案的實現流程如下所述：

步驟1:在一個均勻分布的區間內隨機取k-1個值a1,a2,…,ak-1，令a0=D，構造k-1階多項式q(x)=a0+a1x+a2x2+…+ak-1xk-1;

步驟2：代入{x1=1,x2=2,…,xn=n,n>k}到多項式q(x)，得到n個函數值點對(x1,y1),(x2,y2),(x3,y3),…,(xn,yn);

步驟3:根據拉格朗日插值公式構造的唯一性[15]，通過任意k個函數值點對構造k-1階拉格朗日插值多項式q′(x),q′(x)的常數項就是密鑰數據D。

3 圖像加密-秘密共享方案設計

本文所設計的基于2D-CMCM和(k,n)門限秘密分享技術的圖像加密-秘密共享方案包含3個部分：圖像加密模塊、圖像秘密分享模塊和圖像重構模塊。

3.1 圖像加密模塊算法設計

圖像加密模塊的輸入為原始圖像及如圖1所示的密鑰對，輸出為類似噪聲圖像的加密圖像。本模塊的運行流程如圖2中加密模塊所示。設原始圖像為IM*N，生成加密圖像的詳細步驟如下所述：

步驟1：設置密鑰對{x0,y0,k,α}，通過2D-CMCM產生兩個長度分別為2M和2N的混沌隨機數序列X={x0,x1,…,x2M-1}和Y={y0,y1,…,y2N-1};

步驟2：將隨機數序列X分為兩個子隨機數序列：X1={x0,x1,…,xM-1}和X2={xM,xM+1,…,x2M-1}；將隨機數序列Y分為兩個子隨機數序列：Y1={y0,y1,…,yN-1}和Y2={yN,yN+1,…,y2N-1}；

步驟3：將X1(Y1)按升序排列并將xi,i=0,2,…,M-1(yj,j=0,2,…,N-1)的排列序號數作為待加密圖像對應的第i行(j列)像素下(右)移的行(列)數,通過該過程完成圖像的行(列)置亂，生成圖像I1；

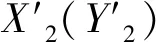
(5)

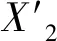
圖1 密鑰對結構Fig.1 Structure of secret keys

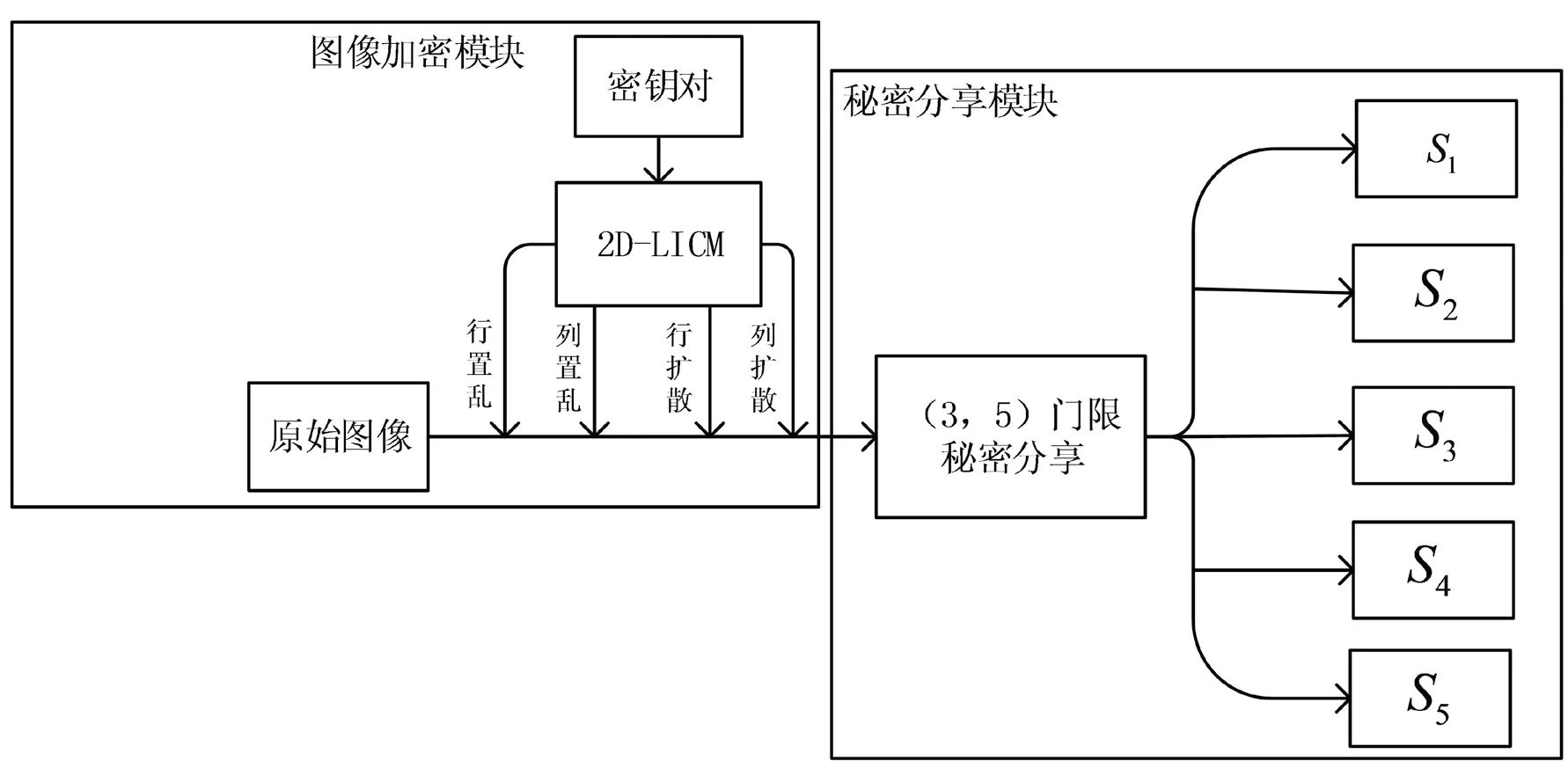
圖2 圖像加密及秘密分享模塊運行流程Fig.2 Running process of imageencryption and secret sharing module

3.2 圖像秘密分享模塊算法設計

圖像秘密分享模塊的輸入為加密圖像I2，輸出為5幅類似噪聲圖像的秘密子圖:S1，S2，S3，S4，S5。首先構造函數q(x)=a0+a1x+a2x2,將a0的值依次設為I2中各像素值，剩余的兩個系數a1和a2從區間[0，255]中任意取得。代入xi,i=1,2,…,5,到q(x)中，生成q(xi,i=1,2,…,5)。按照a0在I2中的行列位置，將q(xi,i=1,2,…,5)作為圖像Si,i=1,2,…,5中對應位置的像素。

3.3 圖像重構模塊算法設計

在原始圖像重構步驟中，只需任意3幅秘密子圖便可以完整復原原始圖像，但少于3幅秘密子圖將不能得到任何信息。該模塊的詳細運行流程如下所述：

步驟1：獲取任意3幅不同的秘密子圖：Si1,i1=1,2,…,5，Si2,i2=1,2,…,5和Si3,i3=1,2,…,5。然后遍歷3幅子圖中的各像素值，通過構造3階拉格朗日插值公式得到其常數項，將常數項作為圖像I2中對應位置的像素值；

步驟2：通過密鑰對{x0,y0,k,α}驅動2D-CMCM，生成與秘密分享階段相同的4個隨機數序列X1，X2，Y1和Y2；

步驟3：通過步驟2生成的4個隨機數序列分別完成行和列的逆向置亂(擴散)操作，生成原始圖像。

4 算法性能分析

以圖片數據集textures中圖片作為測試樣本，本小節展示了本算法在一系列圖像安全算法評價指標上的測試結果，這些指標包括：明文敏感性、密文魯棒性、峰值信噪比(Peak Signal to Noise Ratio,PSNR)和算法執行速度。同時，為了驗證本文所提出算法的安全性和執行效率，將幾種常見的圖像加密算法[3-4,10]與本文所提出的算法進行了比較。本小節包含的所有測試程序均使用Eclipse編譯環境運行。所使用計算機的主要配置如下：Windows10,64位；Core-i7 8809 G,3.1 GHz；64 G內存。

圖片數據集textures中部分樣本圖片如圖3(a)所示。使用本文所提出的算法對textures數據集中圖片進行處理，生成的部分秘密子圖如圖3(b)所示，經過本文算法完成重構之后得到的部分重構圖像如圖3(c)所示。

4.1 安全性分析

4.1.1 明文敏感性分析

明文敏感性分析的目的在于衡量算法對明文攻擊和選擇性明文攻擊這兩種最常見的圖像攻擊方式的抵抗能力。當明文發生微小變化時，若使用同一對密鑰加密原明文圖像和變化后的明文圖像所得到的兩幅密文圖像有顯著差異，則該加密方案的明文敏感性強。

(a)數據集textures中部分樣本圖片(a)Part of sample images in dataset textures

(b)數據集textures中部分秘密子圖(b)Partial secret subgraphs in dataset textures

(c)圖像重構之后得到的部分重構圖像(c)Part of the reconstructed images圖3 部分樣本圖片、秘密子圖及重構圖像。Fig.3 Part of sample images,secret subgraphs and reconstructed images.

以數據集textures中圖片作為測試圖片，每張圖片隨機選擇一個像素點將像素值置為0得到新測試圖片，兩張圖片使用本文算法與參與比較的幾種算法分別進行加密-秘密分享處理，計算原測試圖片得到的5幅秘密子圖和新測試圖片得到的5幅秘密子圖之間的平均NPCR(Number of pixels change rate)，部分圖片的實驗結果列于表1。在理想情況下，兩幅完全不相同的圖像之間的NPCR約為99.6094%。設有兩幅尺寸均為M×N的圖像P、P′，NPCR的定義如公式(6)所示。

(6)

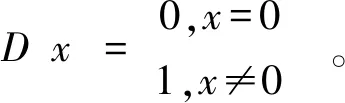
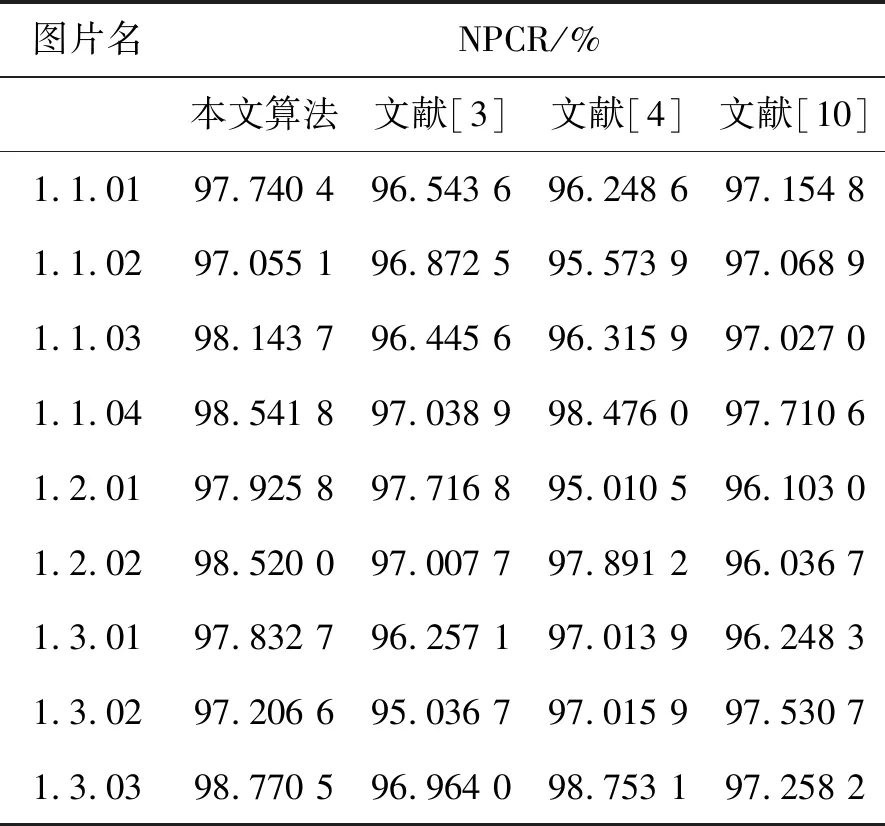
表1 部分樣本圖片的NPCR測試結果Tab.1 NPCR test results for some images

通過表1可以看出，相比于3種參考算法，本文所提出的算法測出的NPCR指標更接近理想值，說明當測試圖像發生微小變化時，通過本文所提出算法進行加密-秘密分享之后生成的秘密子圖與原始測試圖對應的秘密子圖之間具有顯著差異，兩者近似完全不相關。因此，相比于3種參考算法，本文所提出算法具有更高的明文敏感性，對明文攻擊和選擇性明文攻擊具有很強的抵抗能力。

4.1.2 密文魯棒性分析

密文圖像在保存時往往會遭受數據損失攻擊，具有較強魯棒性的圖像保密算法可以在密文圖像部分受損的情況下恢復出具有較高可視性的原始圖像。通過人為將加密得到的密文圖像中部分像素點置0(數量為總像素點數目的1%,2%，4%)，然后進行秘密分享生成秘密子圖，最后觀察重構圖像的可視性，算法的抗數據損失攻擊能力也得到了測試。部分圖片的測試結果見圖4。

通過圖4(b～d)可以看出，密文圖像中部分數據的損失讓密文圖像被污染，這導致了重構圖像的可視性下降，但解密者仍可以從中獲取絕大多數有用信息。因此，本文所提出的算法具有較強的抗數據損失攻擊能力。

(a)密文圖像及其對應的重建圖像(a)Encrypted image and its decrypted image

(b)包含1%數據損失的密文圖像及其對應的重建圖像(b)Encrypted image with 1% data loss and its decrypted image

(c)包含2%數據損失的密文圖像及其對應的重建圖像(c)Encrypted image with 2% data loss and its decrypted image

(d)包含4%數據損失的密文圖像及其對應的重建圖像(d)Encrypted image with 4% data loss and its decrypted image圖4 密文圖像魯棒性分析實驗結果Fig.4 Experimental results ciphertext image robustness analysis

4.2 可逆性分析

峰值信噪比(Peak Signal to Noise Ratio,PSNR)這個指標經常被用于檢驗數字圖像加密算法是否能高質量地恢復加密圖，峰值信噪比越高，說明被重構出的圖像越接近原始圖像。PSNR定義如公式(7)所示。

(7)

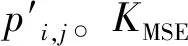
(8)

部分樣本圖片的PSNR測試結果列于表2。由表2可知，本文所提出的算法重建出的圖像與原始明文圖像間的不相同像素點數目在2個以內，遠少于另外幾種參考算法，表明本文所提出的算法具有更高的圖像可逆性，通過秘密子圖能幾乎完整地恢復出原始明文圖像。

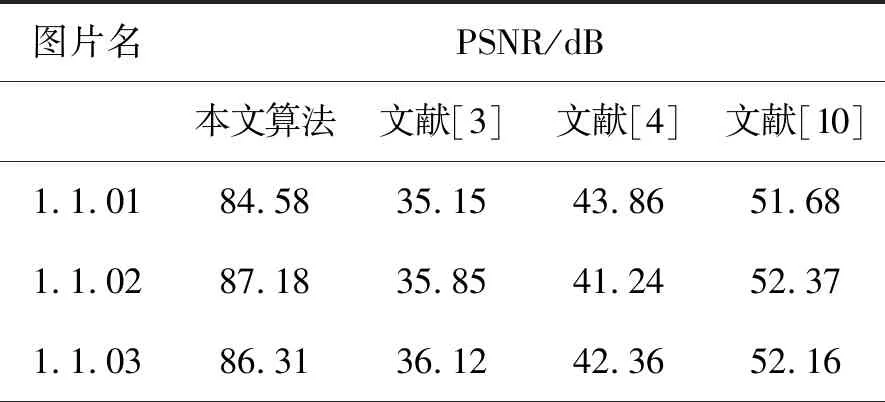
表2 部分樣本的PSNR測試結果Tab.2 PSNR test results of partial samples

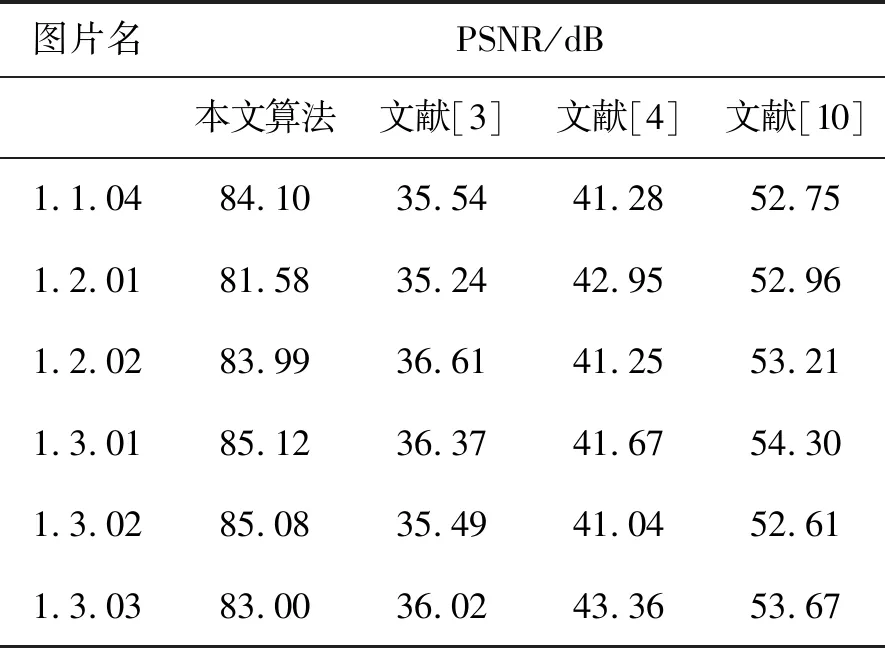
續 表

4.3 執行效率分析

為了實現海量圖片的實時性加密-秘密分享及原始圖像重建，每幅圖像的加密-秘密分享時間及圖像重建時間必須盡可能短。以數據集textures中圖像作為測試樣例，本算法與另外幾種參與比較的算法的加密-秘密分享消耗時間及圖像重建時間列于表3。通過表3可以看出，使用本文所提出算法時，每幅圖像完成加密-秘密分享及重建的總消耗時間均不超過0.5 s，因此本文所提出的算法能夠實現海量圖片的實時分布式秘密存儲。

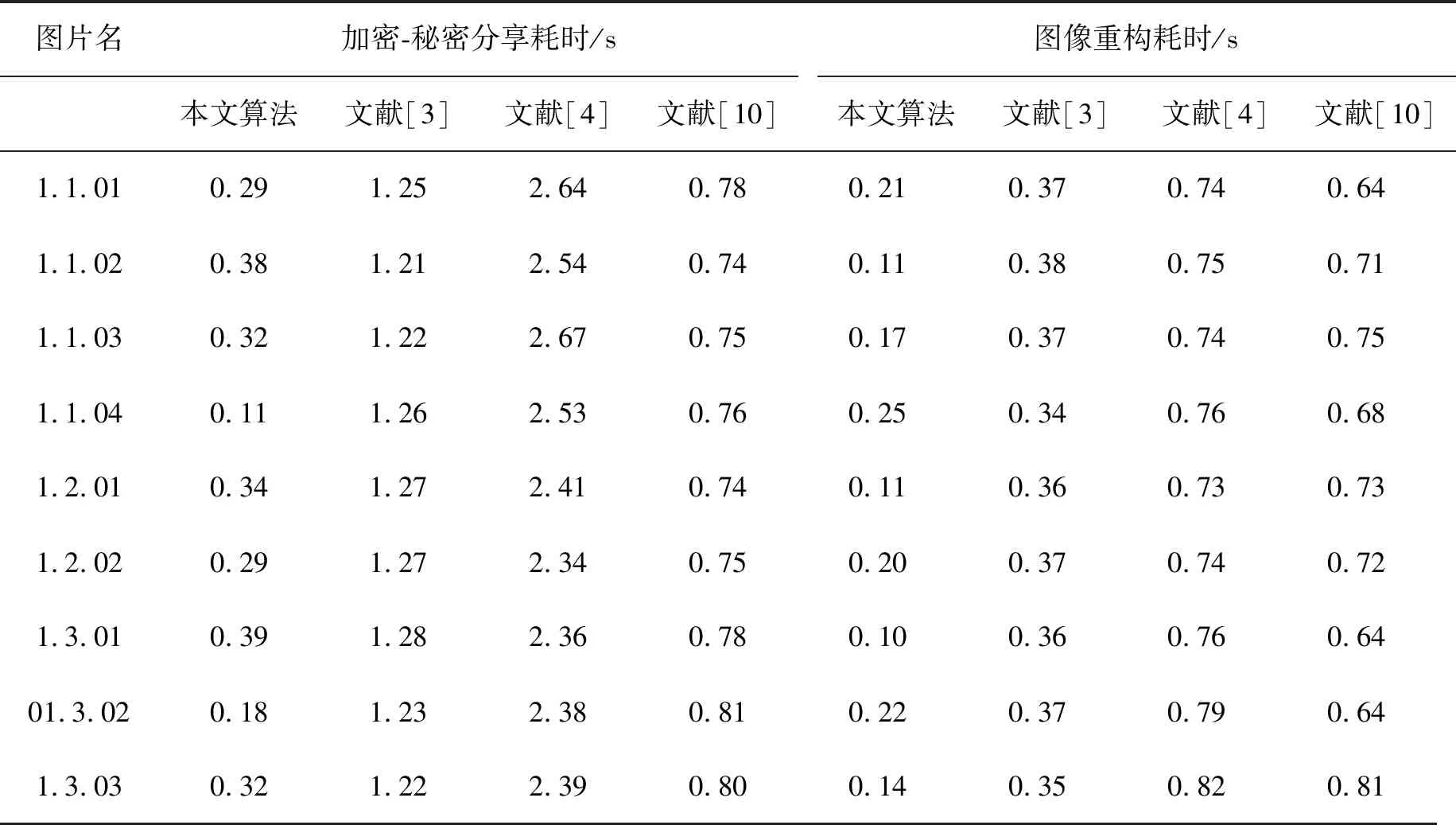
表3 部分圖片執行效率測試結果Tab.3 Execution efficiency of partial samples

5 結 論

為了實現數字圖像的分布式保密存儲，本文提出了一種圖像加密-秘密分享算法。圖像加密包含行/列置亂和擴散兩個步驟，使用2D-CMCM產生的4個隨機數序列完成，通過在行擴散階段使用已加密像素點參與擴散，本文算法的安全性進一步得到了提高。在對圖像加密得到的密文圖像進行秘密分享的階段，使用基于拉格朗日多項式插值的(3,5)門限秘密分享算法，通過帶入5個不同的整數值到多項式，將密文圖像分為5份秘密子圖。解密者只有在獲取不少于3份的秘密子圖及密鑰的情況下才能實現原始圖像的無損重建。在安全性分析實驗中，本文所提出算法顯示出了高度的抗明文/選擇性明文攻擊能力和抗數據損失攻擊能力；在可逆性分析中，秘密子圖被證實可以實現原始明文圖像的無損重構，重構出的圖像與原始明文圖像的差異不超過2個像素點；在執行效率測試實驗中，本文所提出算法的高執行效率也得到了驗證。經過一系列實驗，本文所提出算法的高度實用性得到了證實。