改進回溯搜索優化回聲狀態網絡時間序列預測①

胡 率,肖治華,饒 強,廖榮濤

(國網湖北省電力有限公司 信息通信公司,武漢 430077)

現實世界中存在各種各樣的時間序列數據,分析挖掘數據的隱藏信息,基于合理的假設和推理,建立能夠擬合復雜系統行為的模型,并依據該模型對序列未來的發展規律做出估計和判斷符合科學規律[1].作為時間序列分析的一個研究分支,時間序列預測在實際中廣泛應用.但是,進行時間序列預測依然存在巨大的挑戰,主要原因是時間序列數據往往表現出復雜的特性,比如時序性、高維性、非線性和非周期性等.

人工神經網絡(Artificial Neural Network,ANN)是一種以數據為驅動的、自適應的人工智能模型,它具有非常良好的非線性映射能力.從理論角度來講,ANN可以以任意精度無限逼近任何動態系統的行為[2].ANN幾乎能夠模擬任何線性和非線性的時間序列數據生成過程,因而成為準確且應用廣泛的預測模型[3].

2004年,Jaeger等[4]提出了一種全新的遞歸神經網絡——回聲狀態網絡(Echo State Network,ESN).ESN最顯著特征是網絡訓練過程簡單:只有儲備池(隱藏層)到輸出層的輸出連接權值矩陣需要計算,其他各層之間的連接權值矩陣在網絡初始化階段隨機生成并保持不變.ESN能夠克服傳統遞歸神經網絡的網絡結構難以確定、訓練效率低下、收斂速度慢、容易陷入局部最優等缺點,因而應用廣泛.例如網絡流量預測[5]、變風量空調內模控制[6]和非線性衛星信道盲均衡[7]等.標準的ESN在計算輸出連接權值矩陣時會采用最小二乘估計或者嶺回歸等線性方法,這類方法在節約計算成本的同時會造成網絡過擬合.因此,對ESN的輸出連接權值矩陣進行優化以提升其性能具有現實意義.

本質上,對ESN的輸出連接權值矩陣進行優化是一個離散、高維和強非線性的復雜問題.研究指出進化算法(Evolutionary Algorithm,EA)在解決此類問題時性能卓著.宗宸生等[8]運用改進粒子群算法優化 BP神經網絡的初始權重,建立糧食產量預測模型,該模型具有更高的預測精度和較大的適應度.朱海龍等[9]利用GA優化 BP神經網絡的初始權值和閾值進而建立胎兒體重預測模型,模型收斂速度和預測精度都得到提升.針對ESN的優化,田中大等[5]利用經典的GA對ESN儲備池參數進行優化,進行網絡流量預測時獲得不錯的精度.Chouikhi等[10]應用PSO對ESN的固定權值矩陣進行預訓練,以降低連接權值矩陣在具體應用問題上的隨機性.也有學者使用進化算法對ESN的儲備池到輸出層之間的連接進行優化,例如Wang等[11]提出使用BPSO對ESN的儲備池到輸出層之間的連接進行優化,優化模型在系統識別和時間序列預測問題上獲得更好的實驗結果.本文將從提升ESN的預測精度出發,提出使用自適應回溯搜索算法(Adaptive Backtracking Search Optimization Algorithm,ABSA)對ESN的輸出連接權值矩陣進行優化.

1 相關知識

1.1 回聲狀態網絡

回聲狀態網絡因為其相對簡單的網絡結構、訓練算法和性能而廣受關注.ESN是儲備池計算方法之一,采用“儲備池”作為信息處理媒介,儲備池將網絡的輸入信號映射到高維的復雜動態狀態空間.儲備池的神經元之間的連接在網絡初始化階段隨機生成并在整個訓練過程中保持不變[12].正是由于儲備池計算特征,ESN相對于傳統的RNN具有明顯的優勢.標準結構的ESN如圖1所示,可以分為3個組成部分:一個輸入層(K個神經元),一個儲備池(N個神經元)和一個輸出 層(L個神經元).

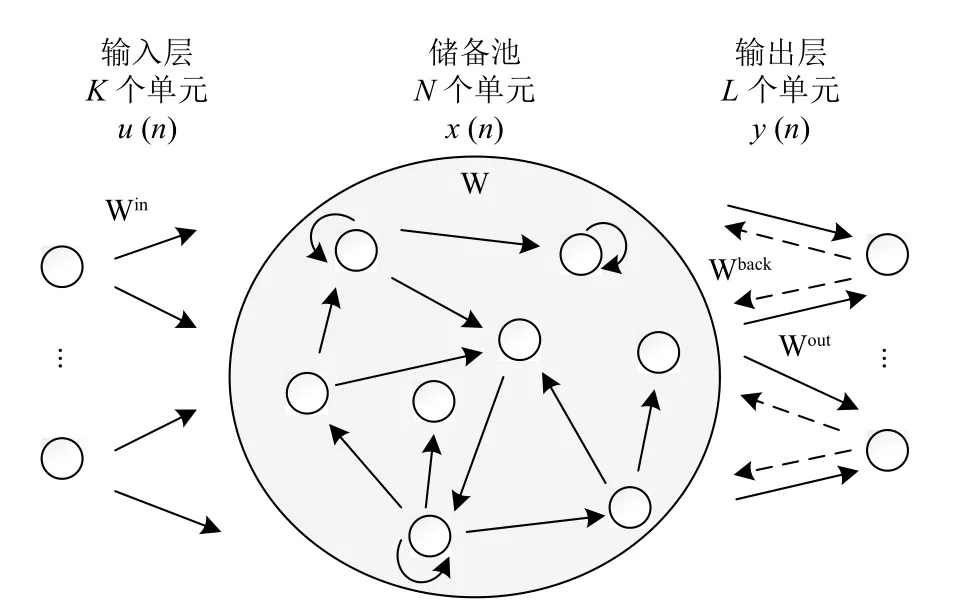
圖1 回聲狀態網絡的標準結構

ESN在時刻n的輸入,儲備池神經元的狀態和輸出層神經元輸出分別表示如下:

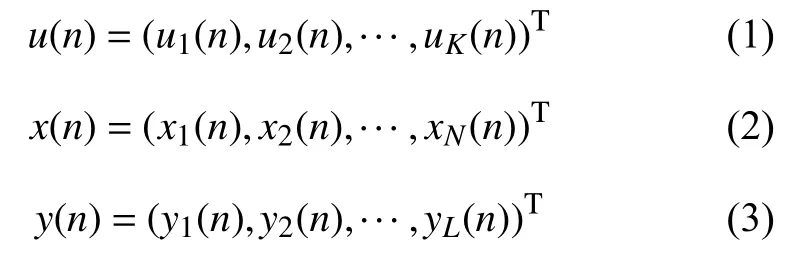
如圖1所示,在標準結構的ESN中,當輸入信號u(n+1)輸 入到網絡時,儲備池內部神經元在時刻n+1的狀態和網絡的輸出分別按照方程(4)和(5)進行更新:

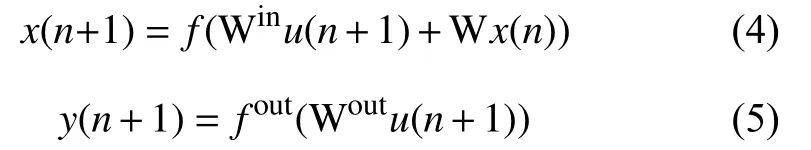
其中,Win(Win∈RN×K)、W (W∈RN×N)和Wout(Wout∈RL×N)分別代表網絡的輸入層到儲備池、儲備池內部神經元和儲備池到輸出層之間的連接權值矩陣.f=[f1,f2,···,fN]表示儲備池中神經元的輸出函數.一般來說,fi(i=1,2,···,N)采用“S-型”函數,比如雙曲正切函數 tanh .fout=[f1out,f2out,···,fLout]表示網絡輸出層神經元的輸出函數.通常情況下,fiout(i=1,2,···,L)會取恒等函數.

1.2 回溯搜索算法及其改進

回溯搜索算法(Backtracking Search optimization Algorithm,BSA)是由Civicioglu在2013年提出的一種屬于進化算法范疇的新智能算法[13].BSA自從被提出就吸引了眾多學者進行研究并應用到不同的領域,比如數值優化[13,14]、自動發電控制[15]和功率流[16]等.標準的BSA主要包括5個基本算子:初始化(Initialization)、選擇I (Selection-I)、變異(Mutation)、交叉(Crossover)和選擇II (Selection-II),其算法流程如圖2所示.

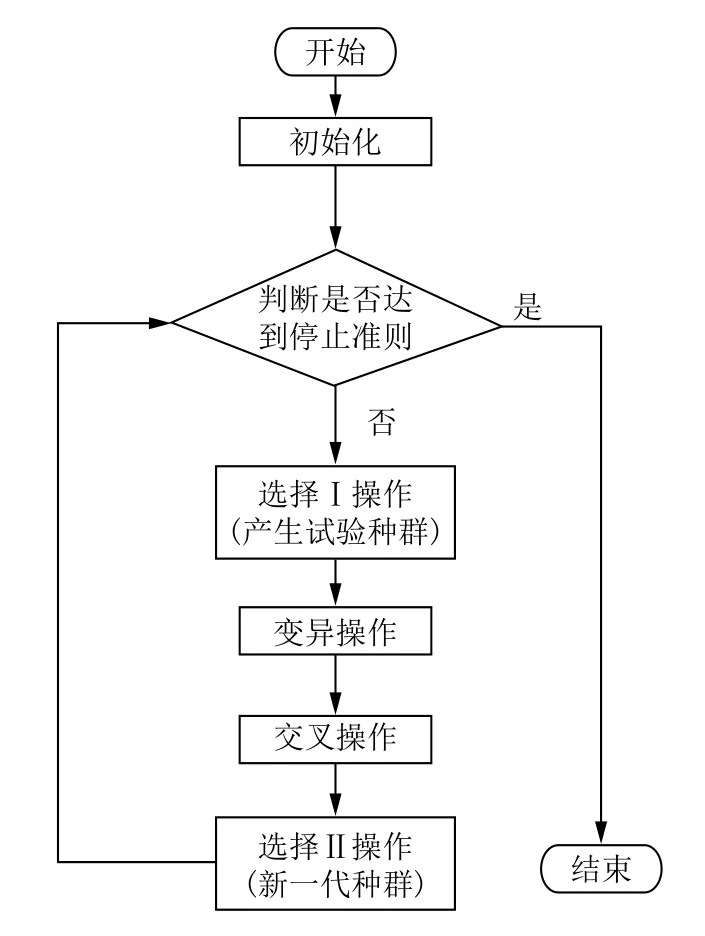
圖2 標準BSA算法流程

在標準BSA中,變異因子F在初始化過程中隨機給定并在整個過程中保持不變,這種策略不能平衡BSA算法的搜索能力和收斂性之間的關系.如果變異因子F取值大,BSA的全局搜索能力會很強而獲得的全局最優解可能展現出低精度.如果變異因子F取值小,BSA在迭代過程中會加速收斂而其全局搜索能力會減弱.可以說,變異因子F是平衡BSA的全局搜索能力和收斂性的關鍵參數.為了充分考慮變異因子F對BSA性能的影響,本文提出自適應回溯搜索算法(ABSA).ABSA使用自適應變異因子策略去替換標準的隨機給定策略,其策略方程表達如式(6)所示:

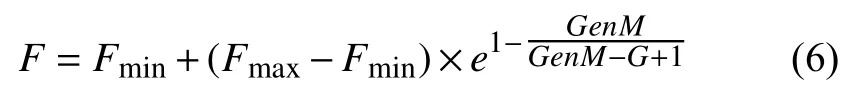
其中,Fmax和Fmin分別代表變異因子F的最大值和最小值.GenM是BSA的最大迭代次數,G是當前迭代次數.e是自然常數.從式(6)可以得出:變異因子 的取值是隨算法迭代過程的進行而不斷改變的.在開始迭代階段,F取值較大用于擴大搜索范圍,保證搜索時種群的多樣性;在隨后的迭代過程中,變異因子F取值逐漸變小,種群的搜索范圍將縮小且種群中已經獲得的優秀個體將會以較大概率被保留.

2 預測模型

2.1 模型介紹

為了驗證本文擬采用的自適應回溯搜索算法優化回聲狀態網絡(ABSA_ESN)的性能,將設計其他的四種預測模型用于與ABSA_ESN進行比較.具體而言,本文將設計以下5種預測模型:

(1)ESN.標準的ESN模型.

(2)GA_ESN.使用遺傳算法(Genetic Algorithm,GA)優化ESN輸出連接權值矩陣.

(3)DE_ESN.使用差分進化算法(Differential Evolution,DE)優化ESN輸出連接權值矩陣.

(4)BSA_ESN.使用標準回溯搜索算法(BSA)優化ESN輸出連接權值矩陣.

(5)ABSA_ESN.使用自適應回溯搜索算法(ABSA)優化ESN輸出連接權值矩陣.

以上5種預測模型中,GA_ESN、DE_ESN、BSA_ESN和ABSA_ESN是四個優化的ESN模型.其中,GA、DE、BSA和ABSA都屬于進化算法(Evolutionary Algorithm,EA)的范疇.

2.2 ESN的優化流程

利用ABSA (GA,DE或者BSA)優化ENS的輸出連接權值矩陣Wout的流程圖如圖3所示.

ESN的Wout優化流程分為以下幾個步驟:

Step 1.設置ESN參數并收集網絡輸入產生的狀態矩陣.

Step 2.設置ABSA (GA,DE或BSA)的參數并生成初始化種群.設置ABSA的初始迭代代數G=0.

Step 3.判斷ABSA (GA,DE或BSA)的迭代是否達到最大迭代次數.如果當前迭代次數G等于最大迭代次數GenM,則ABSA (GA,DE或BSA)的迭代過程結束,獲得最優種群和最優個體;否則,流程繼續執行.

Step 4.依次執行ABSA (GA,DE或BSA)的選擇I (或沒有)、自適應變異(或變異)、交叉和選擇II (或選擇)等幾個操作,獲得當前迭代過程G的新種群.

Step 5.計算新種群中每個個體的適應值,按照貪婪選擇原則更新當前迭代過程的種群.比較當前迭代過程獲得的最優個體與當前獲得的全局最優個體的適應值,適應值較小的將作為新的全局最優適應值且相應的個體更新為全局最優個體.

Step 6.更新G=G+1.返回Step 3.

Step 7.將進化算法獲得的最優個體設置為ESN的最優輸出連接權值矩陣Wout,ESN網絡訓練完成.

Step 8.將測試集中樣本按順序輸入到訓練好的E SN中,進行預測.

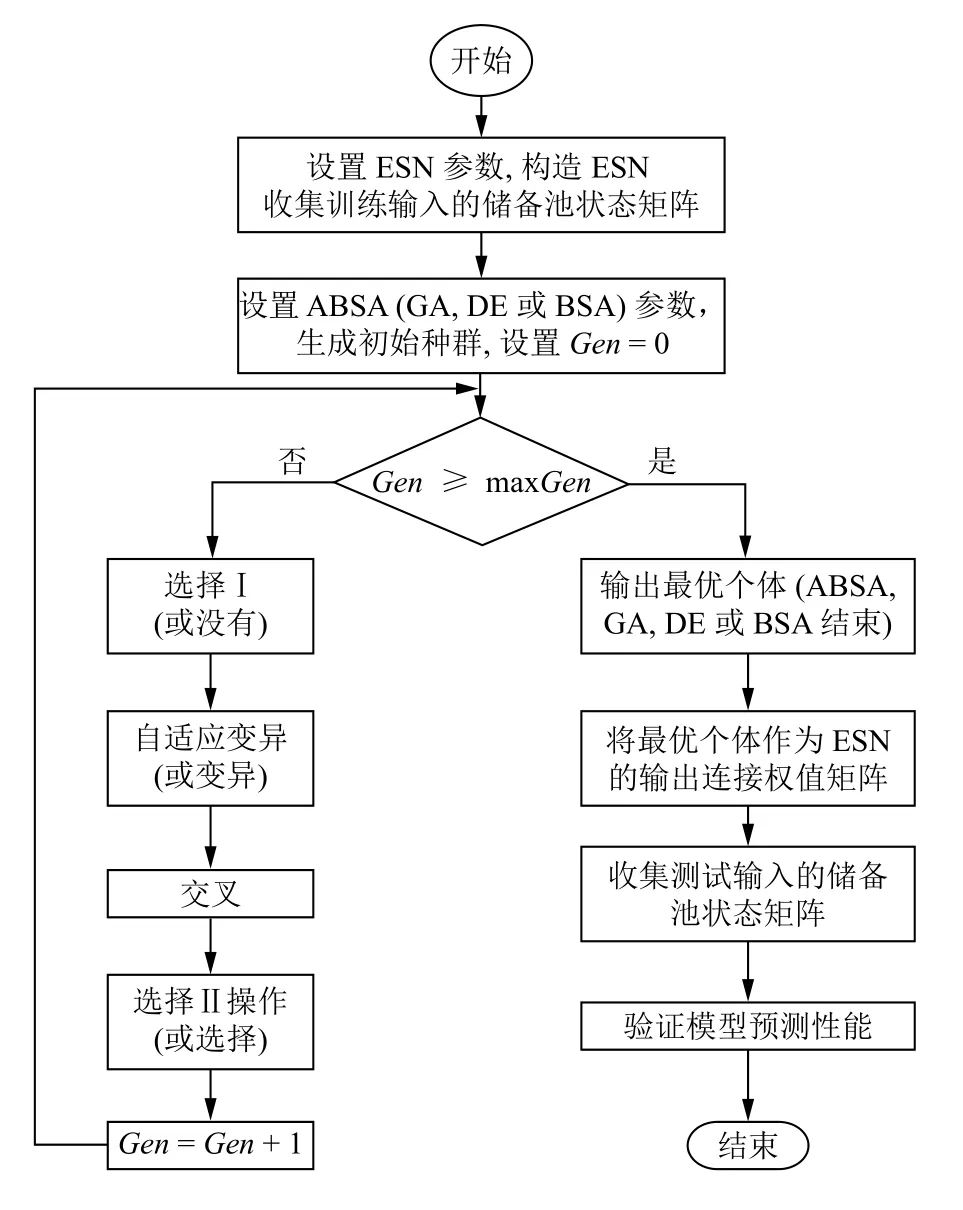
圖3 利用ABSA (GA,DE或BSA)優化ESN的Wout的流程圖

2.3 模型合理性分析及模型比較

本文所采用的5種模型的建模方法在上述2.1和2.2小節已經介紹.本小節將對5種模型進行比較并討論選擇它們的合理性.

(1)ESN是最先進的時間序列預測模型之一.ESN因為其網絡結構簡單、訓練效率高且耦合“時間參數”,因而能夠有效地應用于時間序列預測問題研究.然而,標準的ESN計算地輸出連接權值矩陣容易致使網絡陷入過擬合狀態,影響ESN性能的發揮.

(2)GA_ESN,DE_ESN和BSA_ESN是優化的ESN預測模型.GA、DE和BSA 3種智能算法的算法流程、算子和參數個數不盡相同.使用3種智能算法對ESN進行優化的目的是克服標準ESN容易陷入網絡過擬合狀態的缺陷,增加優化方法的多樣性.相對于GA和DE,BSA在全局尋優時只有一個參數需要設定,在很大程度上能夠簡化算法參數設置過程,進而節約計算成本.

(3)ABSA_ESN是采用改進BSA優化的ESN預測模型.標準BSA的參數變異因子在算法初始化過程中隨機給定并在整個過程中保持不變,這種策略難以平衡BSA算法的搜索能力和收斂速率.ABSA是采用自適應變異因子策略改進的BSA,其能夠有效地克服上述缺陷.具體而言,ABSA在迭代初期變異因子取值較大,能夠擴大搜索范圍從而保證種群的多樣性.此時,ABSA的收斂速度較慢且收斂精度較低.隨著迭代過程的進行,變異因子的取值將逐漸變小,種群的搜索范圍將圍繞已經獲得的優秀個體展開以保證優秀個體將會以較大概率被保留.此時,ABSA的收斂速度和收斂精度逐步加快和提高.總體而言,ABSA_ESN在算法的參數設置、收斂速度和收斂精度上較GA_ESN,DE_ESN和BSA_ESN等均有優勢.

3 數值實驗和結果分析

3.1 實驗設置

為了驗證本文所提出的ABSA_ESN和其他四個用于對比的模型預測性能,兩個混沌時間序列將被采用作為實驗數據集.完成所有實驗的個人電腦配置如下:操作系統是64位Windows 10專業版、處理器是Intel(R)Core(TM)i7-7700 CPU @3.6 GHz和內存為16 GB.運行實驗的軟件環境是Python 3.6和Matlab 2016b.

3.2 數據集及性能評估標準

本文將采用兩個混沌時間序列數據集用于驗證所提出的五種預測模型的性能.第一個混沌時間序列是非線性自回歸滑動模型(Nonlinear Autoregressive Moving Average,NARMA),這是一種有輸入的非線性自回歸移動平均數數列,該模型已經成功應用于非線性系統[17].第二個混沌時間序列是Mackey-Glass時間序列[18].以上兩個時間序列模型經常被使用作為測試時間序列預測算法的性能.

3.2.1 NARMA模型

NARMA模型方程式表示如下:

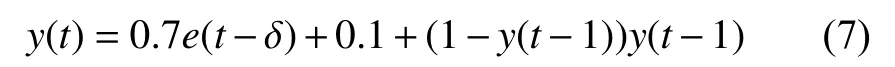
其中,e(t)為獨立分布在( 0,1)之 間的時刻t的模型輸入,y(t)是時刻t的模型輸出,δ 為時滯參數.通常取δ =3.

在本實驗中,我們設定NARMA模型的樣本大小為1000.訓練集、驗證集和測試集樣本的產生過程如下:首先,隨機產生1000個取值范圍在( 0,1)的樣本作為系統輸入e(t).根據式(7)計算出NARMA方程式相應的期望輸出y(t).第二,分別取系統輸入樣本和期望輸出樣本的前80%(樣本編號1–800)樣本作為訓練集樣本.第三,緊接著選取10%(樣本編號801–900)樣本作為確定回聲狀態網絡模型結構的驗證樣本.最后,選取剩余10%(樣本編號901–1000)樣本作為預測集樣本.本文設計驗證集的主要目的是為了在訓練階段選擇合適的ESN模型結構.含有1000個樣本的系統輸入如圖4及其對應的系統輸出如圖5所示.

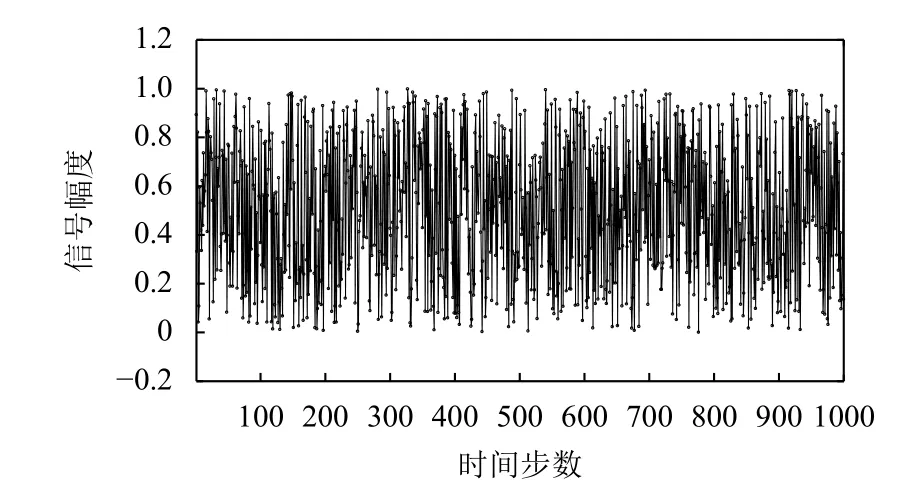
圖4 NARMA模型輸入序列

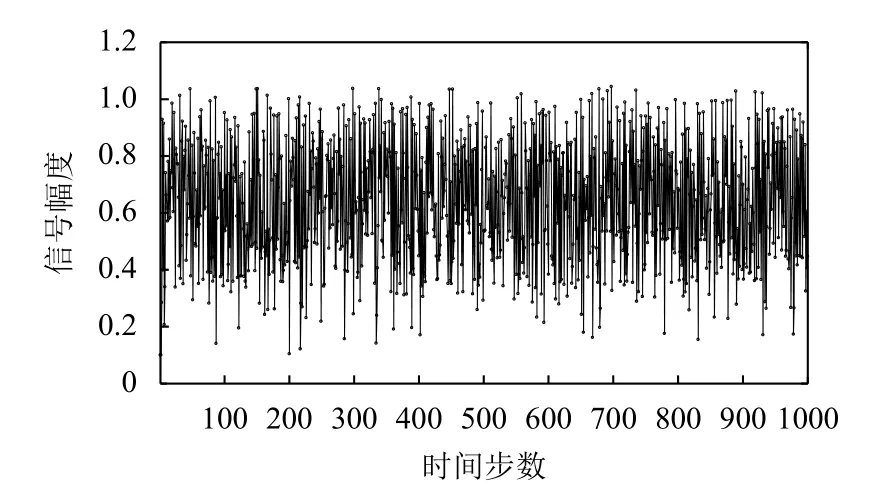
圖5 NARMA模型輸出序列

3.2.2 Mackey-Glass混沌系統

Mackey-Glass時間序列是從時延差分系統導出,其方程如式(8)所示:

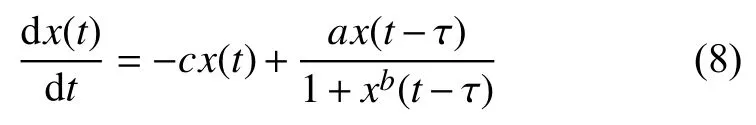
其中,x(t)是時間序列在時刻t時的取值.a、b和c為參數,通常取a=0.2、b=10 和c=0.1.Farmer對Mackey-Glass方程的行為特性做過深入研究,研究結果表明當時滯參數 τ>16.8 時 該方程呈現混沌性,并且τ 值越大,混沌程度越高[19].本文依照一般情況設置時滯參數取值為τ =17.

在本實驗中,我們設定Mackey-Glass時間序列樣本大小為1000.訓練集、驗證集和測試集樣本的劃分同NARMA模型一樣,即編號1–800的樣本作為訓練集,編號801–900的樣本作為驗證集和編號901–1000的樣本作為測試集.使用二階Runge-Kutta方法以步長為0.1構造的樣本長度為1000的時間序列如圖6所示.

圖6 Mackey-Glass時間序列

3.2.3 性能評估標準

用于測量時間序列預測模型性能的指標多種多樣,本文將采用均方根誤差(Root Mean Square Error,RMSE)作為評估預測精度指標,其定義如式(9)所示:

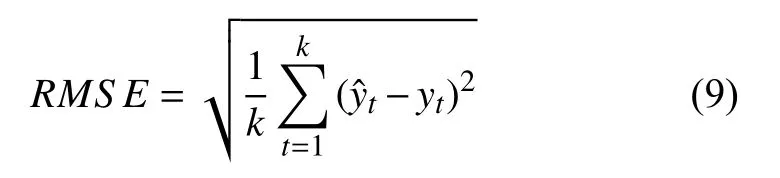
3.3 參數設置與分析

3.3.1 參數設置

本文所提出的預測模型的性能受ESN結構選擇和相應參數設置的影響.結合本文所使用的兩個時間序列數據集的特點,擬采用ESN的結構參數如下:(1)輸入層單元的數目為2(在每個時刻t,ESN有一個常數輸入0.1);(2)儲備池的大小從集合{ 20,30,50}中選擇;(3)輸出層單元數目為1.ESN的其它的參數,比如儲備池內部連接權值矩陣譜半徑SR和儲備池稀疏性SP根據已有文獻的推薦進行設置,即SR=0.8 和SP=5%[12].輸入單元尺度IC及位移尺度IS分別設置為IC=0.3和IS=?0.2.

關于BSA和ABSA的參數設置主要是基于一列實驗和已有參考文獻的推薦.BSA和ABSA的具體參數設置如下:(1)種群大小均設置為100;(2)最大迭代次數均設置為100;(3)交叉概率mixrate均設置為1.0[13];(4)BSA的變異因子F設置為F=3?randn(randn∈N(0,1),N(0,1)是標準正太分布)[13],而ABSA的最大和最小的變異因子分別設置為0.9和0.1.另外,GA和DE的參數分別設置如下:(1)種群大小設置為100;(2)最大迭代次數設置為100;(3)交叉概率為0.6;(4)變異概率為0.01.

3.3.2 自適應變異因子F取值分析

ABSA的變異因子F取值如圖7所示.從圖中可以看出,在算法迭代初期變異因子F取值較大(第一個迭代階段,F取值為最大設定值0.9).此時,ABSA的種群中的個體以較大概率進行變異,ABSA主要是在種群個體空間中進行全局尋優,形成的新種群個體隨機分布在個體空間之中且個體之間的關聯性較小.可以說,ABSA在迭代初期的全局尋優能力非常強而局部尋優能力非常弱,種群個體的相似性很小.隨著迭代過程的更迭,變異因子F取值逐步減小,ABSA種群中的優秀個體逐漸沉淀并且這些優秀個體以逐漸減小的概率進行變異.此時,ABSA逐漸由全局尋優轉變為局部尋優.新種群的形成主要是圍繞已經獲得的優秀個體進行局部尋優.即隨著迭代的進行,ABSA的局部尋優能力逐漸加強而全局尋優能力逐漸減弱,種群個體的相似性逐漸加強.直到迭代進行到后期(圖7中的迭代次數達到90次左右),變異因子F取值趨于穩定(最小設定值0.1),ABSA已經由全局尋優過渡到局部尋優.此時,ABSA全局尋優能力非常弱而局部尋優能力非常強.所以,ABSA的自適應變異因子取值策略能夠平衡算法的全局尋優能力和局部尋優能力.

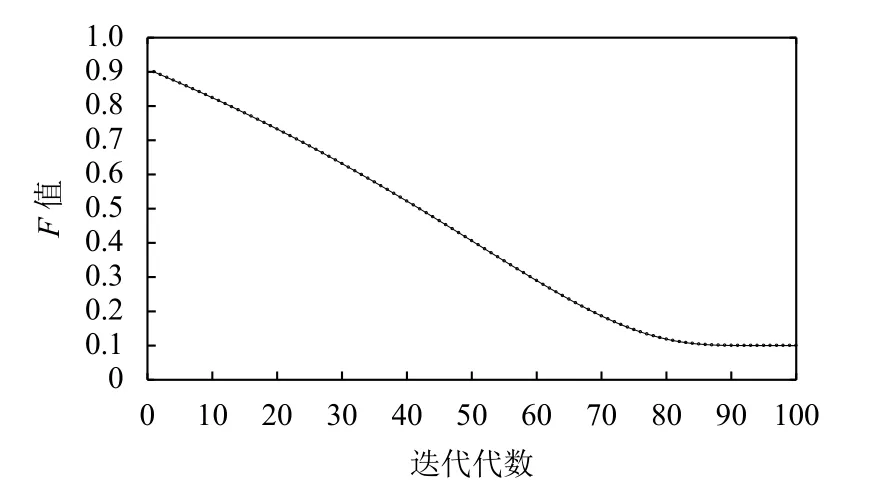
圖7 ABSA的變異因子F取值曲線

3.4 參數設置與分析

對于本文所使用的5個預測模型中的每個預測模型,在訓練階段由于ESN儲備池大小不同而會設計3個候選模型結構,并且根據驗證集的結果選擇一個最優模型結構作為該預測模型的最優結構.表1給出所有5種預測模型的最優模型結構.5種預測模型在兩個時間序列數據集上的性能分別如圖8 (NARMA模型)和圖9 (Mackey-Glass混沌系統)所示,其中“Actual”代表時間序列數據集的期望值.在以RMSE為誤差度量評價標準的前提下,5種預測模型在兩個時間序列數據集上的誤差如表2所示(最優的預測結果用黑體特別標注).

表1 5種預測模型的最優模型結構

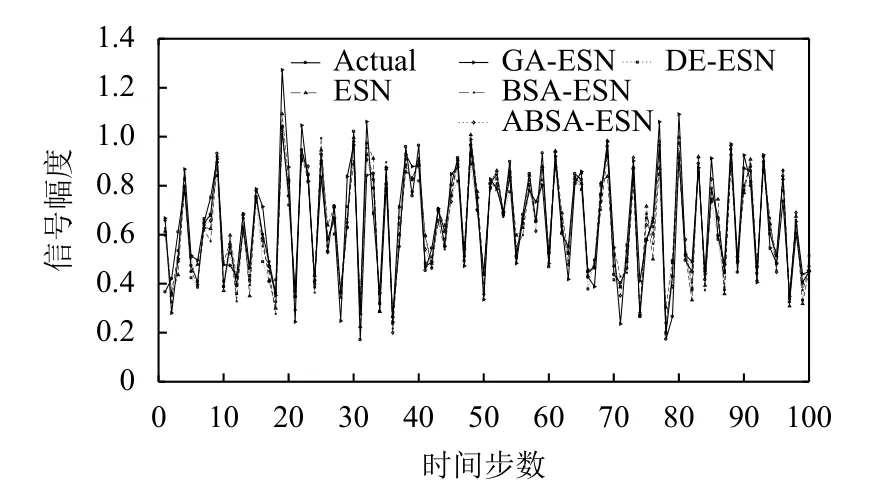
圖8 NARMA上5種模型的預測值和期望值

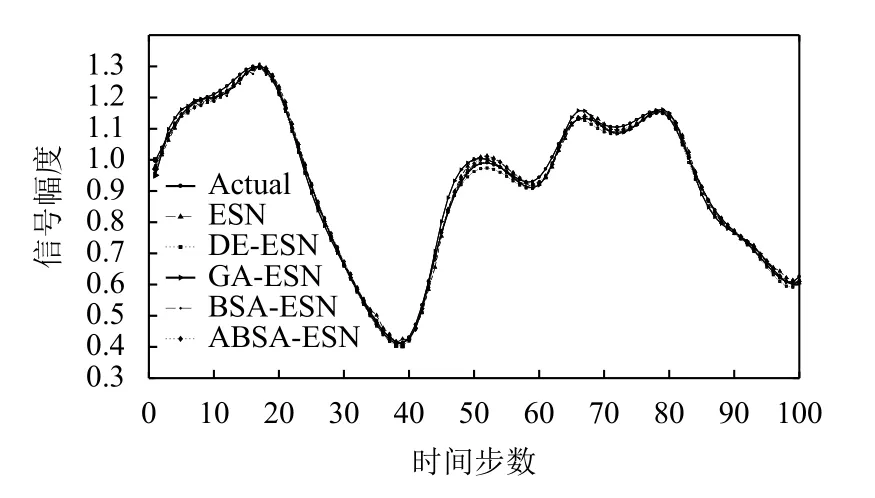
圖9 Mackey-Glass上5種模型的預測值和期望值

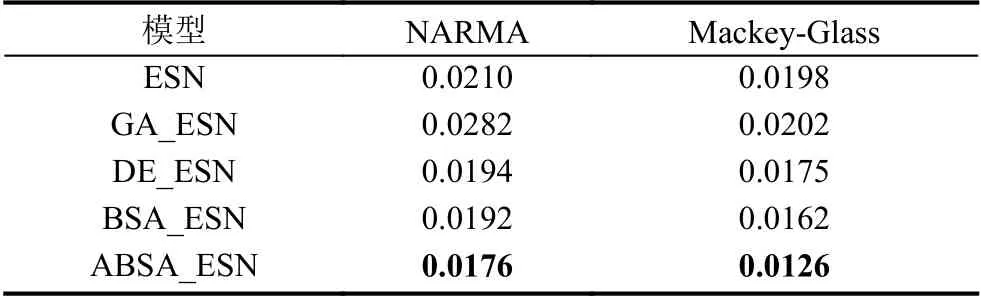
表2 5種預測模型的最優結果(以RMSE為度量方式)

為了評估兩個相比較模型之間的性能差異,相對誤差將被采用作為度量方法.相對誤差是一種流行的用于比較兩個方法之間的性能的度量方法[20].對于兩種方法A(基本方法)和B(對比方法),其誤差分別記為δA和 δB,則相對誤差為相對誤差小于0,說明對比方法B比基本方法A性能更優.另外,相對誤差的平均指兩種比較方法在兩個或兩個以上數據集上的相對誤差的平均值.相對誤差的均值小于0說明對比方法B相對于基本方法A在所有數據集上預測性能有改進.

3.4.1 優化的ESN與標準的ESN

在本文中,為了驗證所提出的使用進化算法優化的ESN (GA_ESN、DE_ESN、BSA_ESN和ABSA_ESN)與標準的ESN之間的預測性能差異,將使用標準的ESN作為基本方法,使用GA_ESN、DE_ESN、BSA_ESN和ABSA_ESN作為對比方法進行預測性能比較.表3給出了兩兩比較模型之間的相對誤差.

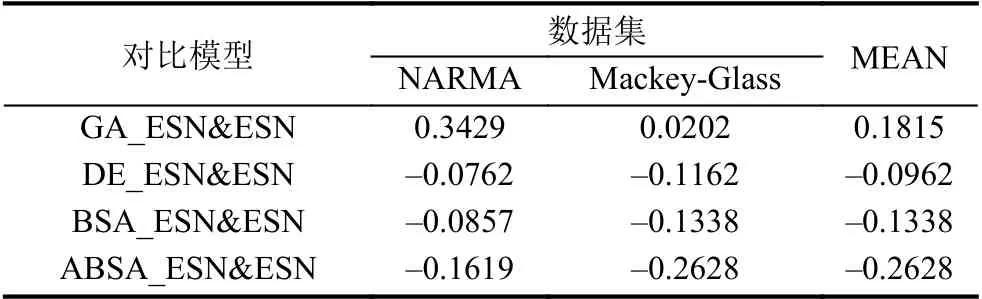
表3 兩種比較模型之間相對誤差(以ESN為基本方法)

從表3可以得出:標準的ESN預測模型無論是在單個數據集還是在兩個數據集作為整體的性能評估中,其性能都只比GA_ESN優越而比DE_ESN、BSA_ESN和ABSA_ESN等預測模型差.具體而言,GA_ESN相對于ESN的性能單獨在NARMA和Mackey-Glass上分別下降34.29%和2.02%,在兩個數據集的整體性能上平均下降18.15%(如表3最后一列“MEAN”所示).而DE_ESN、BSA_ESN和ABSA_ESN相對于ESN單獨在兩個數據集上的性能分別提升7.62%/11.62%、8.57%/18.18%和16.19%/36.36%,在兩個數據集的整體性能上平均提升9.62%,13.38%和26.28%(如表3最后一列“MEAN”所示).總體來說,使用進化算法對ESN的輸出連接權值矩陣Wout進行優化能夠提升ESN的預測性能.

3.4.2 ABSA_ESN與其他4種模型

由3.4.1小節可知,使用進化算法對ESN的輸出連接權值矩陣Wout進行優化相對于標準的ESN具有一定的性能優勢.本節將具體討論本文所提出的ABSAESN相對于標準的ESN和其他3種優化的ESN的優勢體現.具體而言,將ABSA-ESN作為對比方法,而ESN、GA-ESN、DE-ESN和BSA-ESN等分別作為基本方法,然后比較它們兩兩之間的模型性能.表4列出了兩兩相比較模型之間的相對誤差.

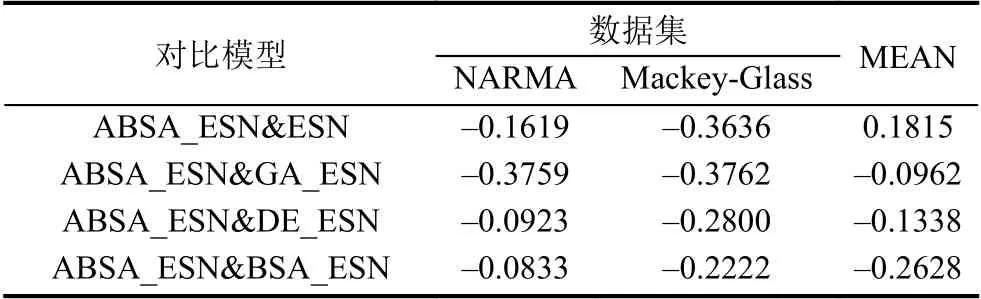
表4 兩種比較模型之間相對誤差(以ABSA_ESN為對比方法)

從表4可以得出:ABSA_ESN預測模型比所提出的其他4種預測模型ESN、GA_ESN、DE_ESN和BSA_ESN的預測精度大幅提升,具體體現在以下兩個方面:

(1)當單獨關注NARMA或者Mackey-Glass數據集時,ABSA_ESN能夠比ESN、GA_ESN、DE_ESN和BSA_ESN等模型在兩個數據集上都能獲得更好的預測結果,主要表現在ABSA_ESN在兩個數據集上的預測精度提升比例分別為16.19%/36.36%、37.59%/37.62%、9.23%/28%和8.33%/22.22%.

(2)當關注所有5種預測模型在兩個數據集上的總體性能時,ABSA_ESN模型比其他4個模型在預測精度上也有大幅提升.ABSA_ESN模型相對于ESN、GA_ESN、DE_ESN和BSA_ESN等模型的平均相對誤差提升比例分別為26.28%、37.61%、18.64%和15.28%.這個信息如表4中最后一列“MEAN”所示.

由此可見,本文提出的使用自適應回溯搜索算法優化的回聲狀態網絡模型(ABSA_ESN)能夠比未優化的回聲狀態網絡模型(ESN)和采用其他進化算法優化的回聲狀態網絡模型(GA_ESN、DE_ESN和BSA_ESN)在兩個混沌時間序列數據集上獲得更好的預測精度.

4 結束語

本文提出使用自適應回溯搜索算法優化回聲狀態網絡的時間序列預測模型(ABSA_ESN),以解決標準回聲狀態網絡中使用的線性方法求解輸出連接權值矩陣容易陷入過擬合的問題,從而提升回聲狀態網絡的預測性能.為了驗證本文所提出ABSA_ESN在時間序列預測問題上的可行性和有效性,本文還設計了4種預測模型用于比較,它們分別是標準的回聲狀態網絡(ESN)、遺傳算法的優化回聲狀態網絡(GA_ESN)、差分進化算法優化的回聲狀態網絡(DE_ESN)和標準回溯搜索算法優化的回聲狀態網絡(BSA_ESN).通過對實驗結果進行分析可以得出如下結論:(1)使用進化算法優化的ESN (GA_ESN、DE_ESN、BSA_ESN和ABSA_ESN)相對于標準的ESN在預測性能上具有一定的優勢;(2)ABSA_ESN相對于4種對比模型能夠獲得更好的預測精度.值得注意的是本文使用的是基本結構的回聲狀態網絡,其自身性能可能會受到一定的限制.在未來,可以研究使用其他更加有效的進化算法優化具有復雜結構的回聲狀態網絡的輸出連接權值矩陣,進一步提升回聲狀態網絡的性能.