基于小波變換動態時間規整的近紅外光譜模型傳遞方法

王其濱，楊輝華,，潘細朋，李靈巧,*

(1.桂林電子科技大學 電子工程與自動化學院，廣西 桂林 541004；2.北京郵電大學 自動化學院，北京 100876)

近紅外光譜分析技術因具有實時、高效、低成本以及不破壞樣本等優點，被廣泛應用于食品、藥品、化工等領域[1-4]。該技術通過建立分析模型，將訓練樣本的近紅外光譜與物理化學性質相聯系，可計算出未知樣本對應的性質參數[5]。

模型傳遞方法是近紅外光譜分析技術中一個常見并具有重要意義的技術問題[6]。通常在實際的應用中，因為測量環境的改變或光譜儀器在制造過程的機械差異等原因，源機(Master)上建立的定量分析模型應用于目標機(Slave)測量的光譜數據時會產生較大的偏差[7]，不能得到正確的預測結果。如果在目標機上再次測量多組樣本數據建立定量模型則費時費力[8]，此問題嚴重阻礙了近紅外光譜儀在實際生產中的應用，而模型傳遞技術很好地解決了這一問題。模型傳遞是建立源機與目標機上測量光譜之間的數學模型[9]，該模型通過對目標機上的近紅外光譜進行轉換，可將其用源機上建立的模型進行參數分析。模型傳遞方法主要分為有標樣和無標樣模型傳遞。目前，有標樣模型傳遞算法應用更為廣泛，如直接校正算法(DS)[10]、分段直接校正算法(PDS)[11]以及Shenk's算法[12]等。DS算法通過選取少量樣本建立標樣集，將目標機上測量的全光譜數據轉換成源機光譜數據來構建校正模型[13]。PDS算法在目標機光譜中增加窗口限制[14]，選取窗口內光譜波長點轉換成源機光譜，代替DS算法中全光譜進行校正。Shenk's算法利用某波長點周圍的光譜數據來計算該波長的校正參數。

光譜儀器采集的光譜數據集普遍存在基線漂移、隨機噪聲、漫反射等現象，如果直接對光譜進行建模分析，會出現模型傳遞效果差、不穩定等問題，故本文嘗試對光譜數據進行小波變換預處理。小波變換作為一種源于傅里葉變換的信號處理工具[15]，為一種時間和頻率的局域變換，因而能有效的從信號中提取信息[16]。小波可以沿時間軸前后平移，也可以按比例伸展和壓縮以獲取低頻和高頻小波，從而對函數或信號進行多尺度細化分析[17]。通過一維小波連續變換對近紅外光譜進行預處理，能夠實現對光譜數據平滑、降噪以及消除基線漂移的處理。動態時間規整算法是一個優化問題[18]，算法通過計算兩個序列點之間最佳的對應關系，獲得代價矩陣最小時的規整路徑。在近紅外光譜領域，由于設備老化、機械誤差以及溫度濕度等條件的影響，源機與目標機測得的光譜之間不但會產生基線漂移，而且波長點也會產生偏移[19]。通過尋找源機光譜與目標機光譜的最佳對應關系，可以建立更精確的校正模型。

1 WDTW算法

WDTW模型傳遞方法，首先將光譜進行小波變換預處理，然后計算源機光譜與目標機光譜上各個波長點的相關距離，通過DTW算法找到源機光譜與目標機光譜各個波長點的關聯關系，使得整體的相關距離最小，最后再根據此關聯關系構建回歸模型。通過在近紅外藥品光譜數據集和汽油光譜數據集之間進行傳遞模型實驗，實驗結果相較于傳統方法光譜差異和預測標準偏差均有所降低。

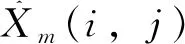
1.1 波長點相關距離計算

設兩個序列分別表示為X=(x1,x2,x3,…,xN)和(y1,y2,y3,…,yM)。DTW算法可以將序列X和Y中的點進行最佳匹配，使兩序列點之間的距離和最小。序列和匹配關系示意圖如圖1所示。

圖1 序列的匹配關系Fig.1 The matching relation of sequence

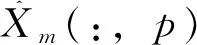
(1)

式中，Cov表示光譜序列之間的協方差，Var表示光譜序列的方差。源機光譜和目標機光譜序列之間的相關距離可根據相關系數求出：

(2)

DTW算法通過構造一個代價矩陣C∈RN×M表示序列X與序列Y中每個元素之間的距離。

C∈RN×M∶ci,j=Di,j

(3)

通常在語音識別領域，DTW算法是通過ci,j=‖xi-yi‖計算元素之間距離，而光譜數據更關注于兩個光譜序列波長點的相關性，因此用相關距離Di,j。

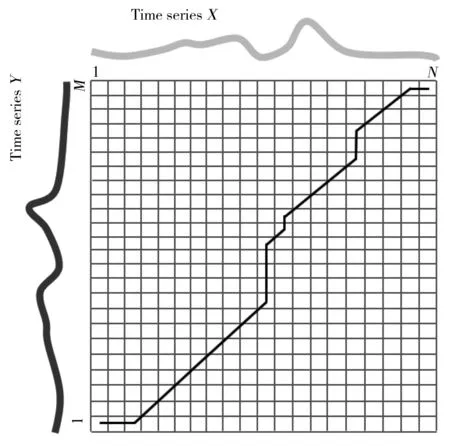
圖2 最佳規整路徑Fig.2 The optimal warping path

1.2 規整路徑的計算

根據代價矩陣，DTW算法能夠找到元素之間相關距離最小的路徑，該路徑代表了元素之間的最佳對應關系。圖2表示了兩個序列X和Y的最佳規整路徑示意圖。

規整路徑的計算必須滿足3個條件：

① 邊界限制：規整路徑必須從(1,1)點出發，在(N,M)點結束。

② 順序限制：規整路徑需要按照順序匹配，不能交叉或跳過某點進行匹配。

③ 單調限制：路徑匹配過程中，只能向右、向上或者右上方向移動，以避免無意義的循環。

如順序限制和單調限制條件：設當前點為(i,j)，下一個將要匹配的點只能是(i+1,j)、(i,j+1)或者(i+1,j+1)。規整路徑中相關聯點代價的和即為DTW算法的損失函數：

(4)

DTW算法要求解的就是使關聯代價最小化：

DTW(X,Y)=min{cp(X,Y),p∈PN×M}

(5)

通過應用動態規劃來求解累加距離最小的路徑，其計算公式如下：

D(i,j)=min{D(i-1,j-1),D(i-1,j),D(i,j-1)}+c(xi,yj),i∈[1,N],j∈[1,M]

(6)

式(6)中,c(xi,yj)為當前所在點的關聯代價，累加距離最小即為其與前一匹配點相關距離的最小值之和。累加距離最小的路徑即為規整路徑。

1.3 校正模型的建立

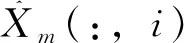
(7)

(8)

通過PLS方法求得方程系數，將源機光譜點分別做如上運算，然后將求得的全部系數保存于矩陣F，F即為模型傳遞所求的傳遞矩陣。通過如下公式即求得傳遞后的光譜。

(9)

2 實驗部分

2.1 實驗數據

分別采用藥品和汽油2個數據集驗證了WDTW模型傳遞方法的有效性。數據集1是由國際漫反射會議(IDRC)公布的藥品近紅外光譜數據集(http://www.eigenvector.com/data/tablets/index.html)，包括了藥品的活性、重量和硬度3個性質參數。數據集2是由中國石油化工股份有限公司石油化工科學研究院提供的汽油近紅外光譜數據集，其包括了汽油C7、 C8、 C9、C10 4個成分的性質參數。2個數據集樣本數、樣本維度、波長范圍及波長間隔如表1所示。

表1 實驗數據集的詳細介紹Table 1 Detailed introduction of experimental data

2.2 數據預處理

光譜儀器采集的光譜數據集普遍存在基線漂移、隨機噪聲、漫反射等現象，故需要對光譜數據進行預處理。預處理過程首先采用數據平滑消除光譜數據中可能存在的隨機噪聲(平滑窗口為17，多項式階數為3)，然后再使用小波變換(小波尺度Scale為4，母小波波長為32*Scale)進行數據處理。

2.3 建立定量模型及評價指標

采用K-S算法選取藥品和汽油數據的標樣集，通過計算近紅外光譜之間的歐氏距離，選取最具代表性的光譜樣本子集即為標樣集。首先將實驗數據成分進行排序，然后采用隔三取一的方式從汽油數據集中選取60個測試集，28個校正集；同樣從藥品數據集中選取460個測試集，155個校正集。最后采用10折交叉驗證，據預測標準偏差(SEP)得到最優的PLS模型主因子數，用PLS建立源機定量模型。采用光譜平均差異(ARMS)、預測標準偏差(SEP)和光譜校正率(Prcorrected)作為WDTW模型傳遞方法的評價指標。其中，ARMS越小，說明兩個不同的光譜儀器測得的光譜差異越小;SEP越小,表明所建模型的預測能力越強；Prcorrected值越小，代表模型的傳遞效果越好。ARMS和SEP計算公式如下：

(10)

(11)

(12)

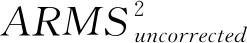
3 結果與討論

3.1 數據預處理結果

實驗預處理過程先采用數據平滑，再進行小波變換處理。前者主要用于消除光譜數據中可能存在的隨機噪聲，后者用于消除數據可能存在的基線漂移。實驗結果顯示，通過將藥品和汽油樣本預處理前后的目標機儀器光譜圖進行對比，可以發現預處理過程能夠有效消除樣本數據間普遍存在的基線漂移、隨機噪聲和漫反射等現象。圖3為預處理前后藥品樣本目標機儀器光譜圖。

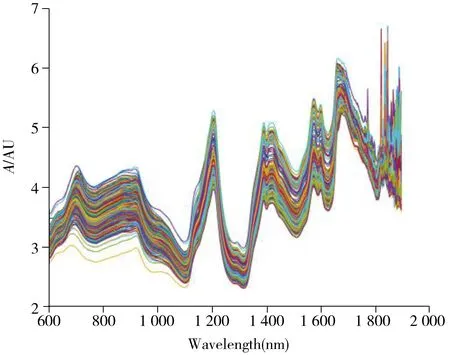
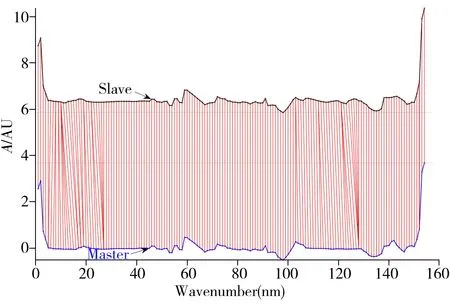
圖4 藥品樣本源機和目標機光譜間波長點匹配關系Fig.4 The match relation of the master and slave instrumental spectrograms wavenumber of the drug sample

3.2 WDTW算法波長點匹配

通過WDTW算法，可以得到源機光譜和目標機光譜波長點之間最優的對應關系。以藥品近紅外光譜數據為例，由于光譜波長點較多，只選取1 000～1 160 nm波長點顯示，其中上方黑色線為目標機光譜(Slave)，下方藍色線為源機光譜(Master)，中間紅色線即連接了源機光譜和目標機光譜之間最優對應關系(見圖4)。從圖中紅色連接線可看到，在波長點10～15 nm、20～25 nm和120～130 nm處，波長點之間發生明顯偏移，而WDTW算法很好地找到了兩者最優的對應關系。WDTW模型傳遞方法基于此對應關系建立了回歸方程。

3.3 模型傳遞前后平均光譜差異對比

使用WDTW模型傳遞方法建立了近紅外光譜校正模型，分別對比汽油、藥品樣本的原始平均光譜圖和傳遞后的平均光譜圖，可以很直觀地看出WDTW模型的傳遞效果。圖5左圖為汽油樣本測試集原始的平均光譜圖，其中實線代表源機光譜，點線代表目標機光譜，可見源機光譜和目標機光譜之間有很大差異，如果直接將源機光譜建立的回歸模型用于目標機光譜數據，必將產生很大誤差。圖5右圖為汽油樣本測試集模型傳遞后的平均光譜圖，源機光譜和目標機光譜之間基本重合，可見WDTW模型傳遞方法減小了兩儀器間光譜的差異。藥品樣本測試集校正前后的譜圖效果與汽油樣品相同，即采用WDTW模型傳遞方法于藥品樣本可有效減小源機和目標機光譜之間的差異。

表2記錄了WDTW算法模型傳遞前后源機和目標機儀器間的光譜差異以及光譜校正率。以汽油C7成分為例，在目標機光譜取標樣集為5，校正前光譜平均差異為0.018 8，校正后光譜的平均差異為0.002 1，通過校正率計算公式(12)可得其光譜校正率為98.75%，WDTW模型傳遞算法可以很好的消除源機光譜和目標機光譜之間的差異。

表2 WDTW算法傳遞前后測試集主從儀器間的光譜差異Table 2 Spectral difference between master and slave instruments before and after test set passing through WDTW algorithm

將WDTW算法與DS、PDS和DTW 3種算法模型傳遞后以及未校正的光譜平均差異進行對比，如表3所示，對比未校正的光譜，發現經過模型傳遞后的平均光譜差異均有減小，其中WDTW算法表現最好，模型傳遞后的平均光譜的差異整體最小，也說明此算法模型的傳遞效果最好。其中汽油樣本經過WDTW算法模型傳遞后，C7、C8、C9和C10 4種成分的平均光譜差異均為0.002 1。在藥品樣本數據集中，WDTW算法同樣取得了很好的效果，藥品活性、重量和硬度在模型傳遞后，平均光譜差異分別為0.026 8、0.025 7、0.026 0。

表3 DS、PDS、DTW和WDTW傳遞后測試集主從儀器間的光譜差異Table 3 Spectral differences between master and slave devices of test set after DS,PDS,DTW and WDTW transmission

3.4 模型傳遞前后預測結果對比

為了進一步驗證WDTW模型傳遞方法的有效性，實驗采用源機光譜數據建立PLS回歸模型，將經過模型傳遞后的光譜數據代入回歸模型，并用預測標準偏差評價模型傳遞的效果。通過與DS、PDS、DTW算法比較(PDS算法的窗口大小用交叉驗證確定),WDTW算法傳遞后，光譜預測結果的預測標準偏差整體最小，模型傳遞效果最好，結果如表4所示。

表4 DS、PDS、DTW和WDTW傳遞后測試集預測標準偏差(SEP)Table 4 Prediction standard deviation(SEP) of the test set after DS,PDS,DTW and WDTW pass

實驗結果顯示，在模型傳遞前，未校正的目標機光譜直接帶入源機光譜數據建立的PLS回歸模型進行預測有較大誤差。通過模型傳遞之后，校正后的光譜數據預測標準偏差均有減小，其中WDTW算法整體的預測標準偏差最小，表明此時所建模型預測能力最好。DS算法通過全光譜建立校正模型，范圍太大容易引起誤差。PDS算法通過限定一個窗口，在窗口范圍內建立校正模型，窗口大小將會直接影響結果的好壞。DTW算法很好的找到源機光譜和目標機光譜的最佳對應關系，其建立的模型相較DS和PDS算法在汽油數據集上有明顯的優勢，但在藥品數據集中表現較差、原因可能是由于未經過數據的預處理，光譜中的一些噪聲會引起DTW算法建立的模型不穩定。而WDTW算法在經過小波變換預處理后，有效消除了樣本數據間存在的基線漂移、隨機噪聲等，之后通過找到波長點最佳對應關系，再根據此對應關系建立校正回歸模型，可以更加精確的求得轉移光譜，實現近紅外光譜模型的傳遞。

4 結 論

本文針對近紅外光譜模型傳遞問題，提出了基于小波變換動態時間規整的模型傳遞方法。該方法首先使用小波變換進行光譜預處理，然后利用動態時間規整算法求得傳遞光譜。通過一維小波連續變換對近紅外光譜進行多尺度細化分析，以實現對光譜數據平滑、降噪以及消除基線漂移的處理。在經過小波變換預處理后，動態時間規整算法通過尋找不同光譜儀器之間波長點最佳的匹配關系并建立回歸模型，求得傳遞矩陣實現模型傳遞。對汽油和藥品兩個數據集進行實驗，證明了該方法能夠消除不同儀器間光譜的平均差異，提高模型的預測能力和通用性。通過與其他模型傳遞方法DS、PDS和DTW算法進行對比后，表明基于WDTW算法所求的參數少，傳遞效果最好，整體性能最優。