臨界阻尼狀態下局部導電體TEM觀測電壓表達式的探討

高 正，李文堯, 熊彩云

(昆明理工大學 國土資源工程學院，昆明 650093)

0 引言

瞬變電磁法(TEM)具有穿透能力強、探測深度大、適應環境能力強、應用領域廣、應用效果好等優點[1]，因此在國、內外廣泛應用于地質調查[2]、資源勘查[3]、工程地質[4]、水文地質[5]、環境地質等領域[6]。臨界阻尼狀態下局部導電體觀測電壓表達式對研究局部導電體在接收線圈上感應電壓的衰減特征和接收線圈的響應特性有重要的參考價值，在研究過程中發現，臨界阻尼狀態下局部導電體觀測電壓表達式存在兩種不同的推導結果，一種可在文獻[7-17]中查得，另外一種可在文獻[18-19]中查得，兩種表達式存在一個符號差異。為了探究原因，筆者對臨界阻尼狀態下局部導電體觀測電壓表達式重新進行了推導。

1 電壓表達式

1.1 表達式推導

臨界阻尼狀態下局部導電體觀測電壓表達式存在兩種不同的結果，文獻[7-17]中的表達式為：

(1)

式中：

B=δ2+2δ/τ+1/τ2

(2)

(3)

A是和地質體有關的常數；L為接收線圈電感；C為接收線圈分布電容；R為接收線圈匹配電阻；t為觀測時間；Vc為觀測電壓；τ為確定Vc(t)衰減速度的特性參數，稱為時間常數。

文獻[18-19]中的表達式為：

(4)

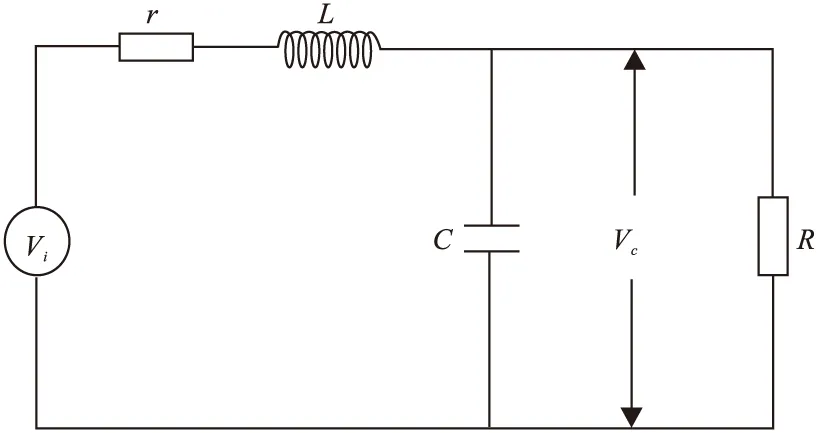
圖1 接收線圈等效電路圖

式中

B=δ2-2δ/τ+1/τ2

(5)

由于式(2)和式(5)存在一個正負號差異，為了驗證式(2)與式(5)的正確，筆者查閱了大量國內、外文獻，沒有查到關于該表達式完整的推導過程，因此對臨界阻尼狀態下局部導電體觀測電壓表達式進行重新推導。

TEM接收線圈等效電路由內阻、電感、分布電容、匹配電阻構成。等效電路圖如圖1所示，電路圖中，Vi為地下地質體在接收線圈上的感應電壓，Vc為觀測電壓，r為線圈內阻，L為線圈電感，C為分布電容，R為匹配電阻。

在電容支路中

(6)

(7)

(8)

對于圖1的等效電路，根據基爾霍夫定律得

Vi=Vr+VL+Vc

(9)

則由式(7)、式(8)、式(9)可得

(10)

式中

(11)

(12)

當t=0時，Vi=0，iL(0-)=iL(0+)，電感電流不能突變，電感等效于開路，電容電壓不能突變，電容等效于短路。因此初始條件為：

Vc(0)=0

(13)

(14)

當Vi=0時，式(10)的特征方程為：

(15)

當線圈工作在臨界阻尼(δ=ωp)情況下，特征方程15)的兩個根分別為:

當δ=ωp時，t1=t2=-δ,則Vi=0時齊次方程(10)的通解為：

Vc=(c1+c2t)e-δt

(16)

當t≥tof時，局部導電體在接收線圈上的感應電壓[8]

(17)

令

(18)

則當t≥tof時，

Vi=Ae-t/τ

(19)

對于非齊次方程式10)，可寫成[8，15，19]

(20)

λ=-1/τ不是特征方程的根，設非齊次方程(20)的一個特解為b1則

Vc=b1e-t/τ

(21)

(22)

(23)

將式(21)、式(22)、式(23)代入式(20)得

(24)

則

(25)

故通解為

(26)

則

(27)

由式(13)、式(26)得

(28)

由式(14)、式27)得

(29)

故

(30)

整理得

(31)

令

(32)

則式31)可寫成

(33)

1.2 MATLAB軟件驗證推導結果

用MATLAB求式20)中Vc表達式的程序如下：

dsolve('D2v+2*a*Dv+a^2*v-c*exp(-t/d)','Dv(0)=0','v(0)=0','t')

輸出結果為：

ans =

(c*d*t*exp(-t/d))/(a*d - 1)- (c*d*t *exp(-a*t))/(a*d - 1)- (c*d^2* exp(-a*t))/(a*d - 1)^2 + (c*d*exp(a*t - t/d)*exp(-a*t)*(d + t - a*d*t))/(a*d - 1)^2

式中：

整理得Vc表達式為：

(34)

令

(35)

則式34)可寫成

(36)

由MATLAB軟件推導的式(35)、式(36)可知，本文推導的式(32)、式(33)是正確的，本文推導的結果與文獻[18-19]中的表達式式(4)、式(5)一致，所以文獻[7-17]中的式(1)、式(2)是錯誤的。

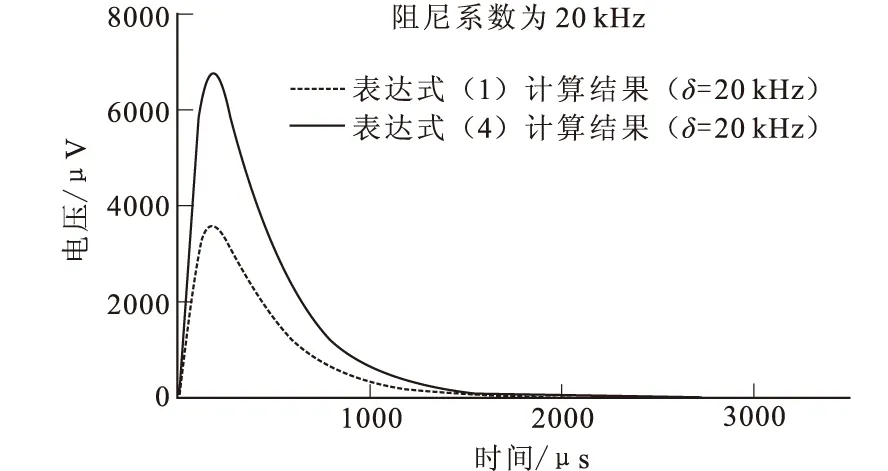
圖2 阻尼系數為20 kHz時計算結果對比圖

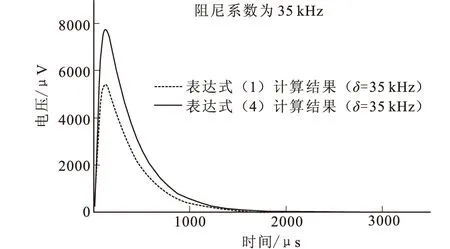
圖3 阻尼系數為35 kHz時計算結果對比圖

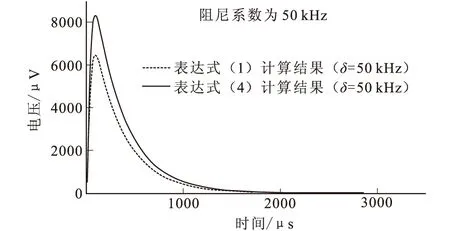
圖4 阻尼系數為50 kHz時計算結果對比圖

2 表達式(1)的誤差分析

由于式(1)被大量文獻引用，因此筆者對表達式(1)計算結果的影響進行研究。由式(2)和式(5)可知，線圈阻尼系數δ和時間常數τ是導致表達式(1)和表達式(4)出現差異的兩個因素，因此對δ和τ對表達式計算結果的影響進行探討。

2.1 線圈阻尼系數δ的影響

設定相關參數的值，并將其分別代入到式(1)、式(4)中,通過計算發現，當時間常數τ的值一定時，隨著阻尼系數的減小，式(1)的計算結果與式(4)的計算結果相比，式(1)計算的誤差越來越大。當阻尼系數在20 kHz～50 kHz(常用小線圈阻尼系數范圍[20])用式(1)計算的觀測電壓誤差達22 %～46 %，詳細計算結果見圖2、圖3、圖4，不同阻尼系數情況下用式(1)計算的觀測電壓相對誤差如表1所示。

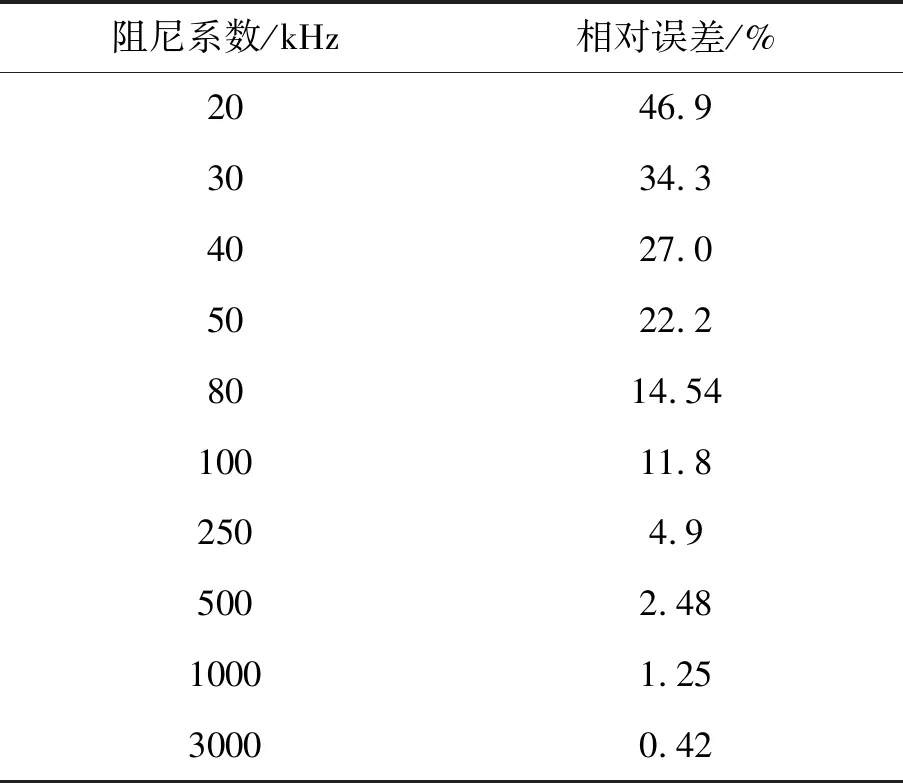
表1 式(1)計算結果相對誤差

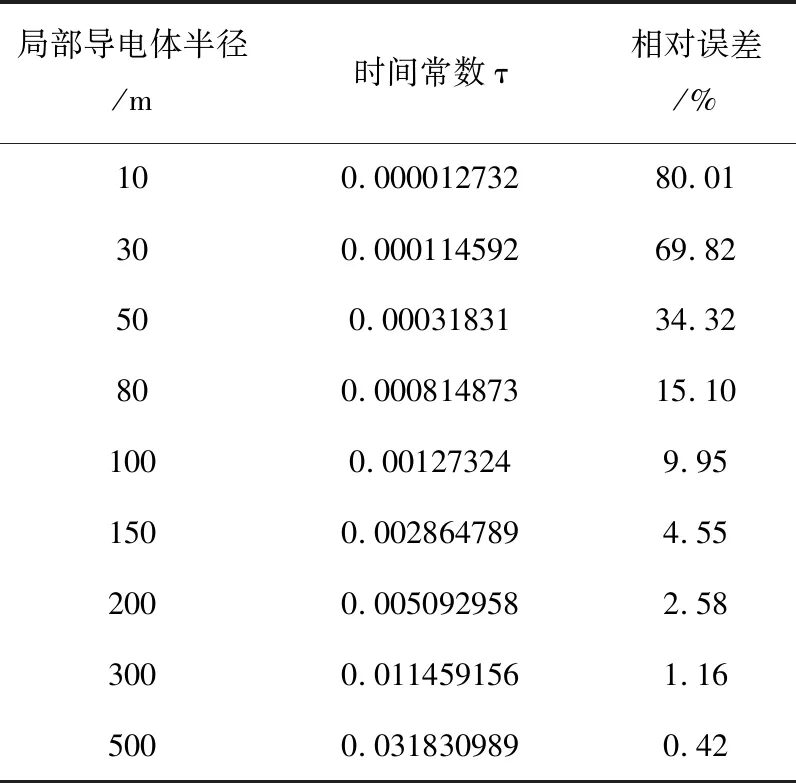
表2 式(1)計算結果相對誤差(δ=30 kHz)

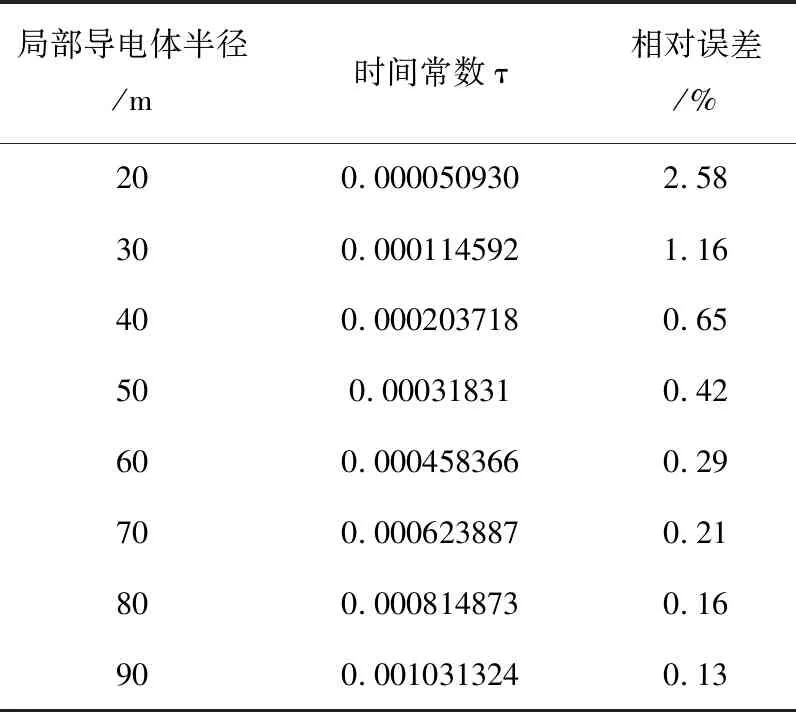
表3 式(1)計算結果相對誤差(δ=3 000 kHz)

由圖2、圖3、圖4可知，式(1)和式(4)計算的觀測電壓曲線形態相似，但是用式(1)計算的觀測電壓值偏低。

由表1可知，隨著阻尼系數的減小，用式(1)計算的觀測電壓的誤差越來越大。

2.2 時間常數τ的影響

時間常數τ的表達式為[8]：

τ=μ0σa2/π

(37)

式中，μ0=4π×10-7H/m為空氣磁導率，σ為電導率，a為局部導電體的半徑。

由于要研究當時間常數τ變化時，式(1)的計算結果與式(4)相比的誤差，且時間常數τ與局部導電體半徑呈正相關，所以取電導率σ為1 S/m，通過變化局部導電體半徑a的值來展開探討。

當阻尼系數一定時，不斷變化局部導電體半徑，式1)計算的觀測電壓值的誤差如表2、表3所示。

由表2、表3可知，當阻尼系數一定時，隨著時間常數τ的值的減小，表達式(1)計算的觀測電壓誤差越大。

3 結論

通過驗證式(1)是錯誤的,不建議使用,式(4)是正確的，建議使用；式(1)和式(4)計算的觀測電壓曲線形態相似；當時間常數一定時，隨著阻尼系數的減小，式(1)計算的觀測電壓誤差越來越大；當阻尼系數一定時，隨著時間常數的減小，式(1)計算的觀測電壓誤差越來越大。