2.5維各向異性介質直流電法異常場的正演模擬

柯頌頌，宋 滔，劉 云

(1.中國科學院 地球化學研究所礦床地球化學國家重點實驗室, 貴陽 550002；2.中國科學院大學，北京 100049)

0 引言

直流電阻率法各向同性的正反演技術已經比較成熟，并且在工程、找礦等領域有了廣泛應用[1-2]。隨著數值模擬技術的發展，研究的熱點聚集到了更符合實際情況的連續介質和各向異性介質。

對連續介質的研究，徐世浙[3]使用有限單元法矩形單元剖分;阮百堯[4]使用三角單元剖分，實現了對連續介質的數值模擬，取得較高精度;劉云[5]在阮百堯的基礎上，使用矩形內剖分四個三角形的剖分方式實現了對連續介質、復雜地形以及復雜模型的數值模擬。

近年來，對各向異性直流電法的研究也越來越多[6-9]。但關于直流電阻率法2.5維各向異性正演模擬的研究相對較少。徐世浙等[3]使用有限單元法對二維各向異性的直流電阻率法進行了模擬;Zhou等[9]使用高斯正交網格(Gaussian quadrature grids)實現了對2.5維復雜各向異性介質的數值模擬，取得較好的精度。由于三維各向異性參數太多，導致基于三維各向異性正演的反演研究工作進展緩慢，所以研究直流電阻率法2.5維的正反演方法成為探索各向異性反演工作的橋梁。在前人的研究中2.5維正演均是基于總場法的，因為異常場法需要求解一次場，而電性各向異性介質點源傅氏空間中的解析解較難求得，所以關于2.5維各向異性介質異常場法的研究較少。

這里給出各向異性介質2.5維總場和異常場的變分問題。在實現異常場法時，因為將點源各向異性介質空間電位轉換到傅里葉空間中具有一定困難，所以筆者進行了簡化處理，假設點源附近的介質為主軸各向異性，從而實現2.5維各向異性介質異常場法的模擬，通過算例證明該方法的正確性。

1 變分問題

一般定義各向異性電阻率為張量形式[11]，如式(1)所示。

(1)

選取如圖1所示的觀測坐標系，z方向為垂直方向，x、y方向為水平方向，假設介質構造為x方向，即沿x方向介質沒有變化，設介質電性主軸的平面x′y′與坐標軸xy平面的夾角為α，此時電阻率張量表達式(1)中旋轉矩陣D為：

(2)

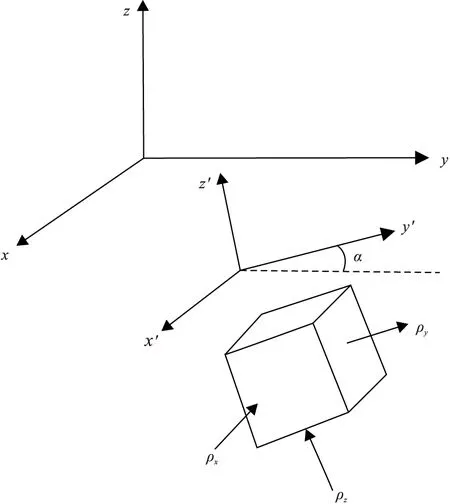
圖1 二維各向異性

將式(2)代入式(1)中得到介質的電阻率張量為：

(3)

相應的電導率為：

(4)

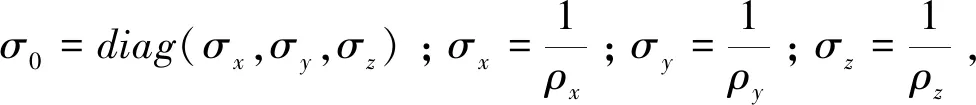
(5)

根據Zhou[9]、嚴波[11]等的推導，傅里葉空間中的電位U滿足的邊值問題如式(6)所示。

(6)

對應的變分問題如式(7)所示。

(7)

當采用異常場法模擬時，將總場分為背景場(一次場)和異常場(二次場)，以消除源的影響，提高模擬精度。

與各向同性的邊值問題和變分問題類似，我們給出異常場滿足的變分問題如式(8)所示。

(8)

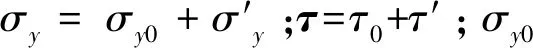
2 有限單元法

2.1 區域剖分

首先將整個區域剖分成矩形單元，然后再將每個矩形剖分成兩個三角形，如圖 2所示。

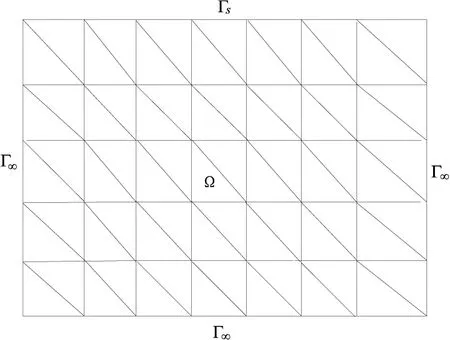
圖2 區域剖分

在三角單元內假設電位是線性變化的，在單元內任意位置的電位u可以通過形函數和三角形三個節點的電位表示，如式(9)所示。

u=Niui+Njuj+Nmum=NTu=uTN

(9)

其中:NT=(Ni,Nj,Nm)為形函數；uT=(ui,uj,um)為三角形節點的電位。

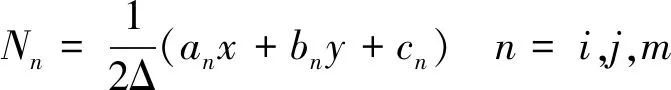
其中：Δ為三角形的面積，且有：

2.2 單元分析

將式(8)中的積分在區域離散化，表示成所有單元的線性組合如式(10)所示。

(10)

式(10)中的積分項依次記為積分1、2、3、4、5和6。

根據嚴波[11]等的推導，以及積分1和積分4的相似性，得到：

(11)

(12)

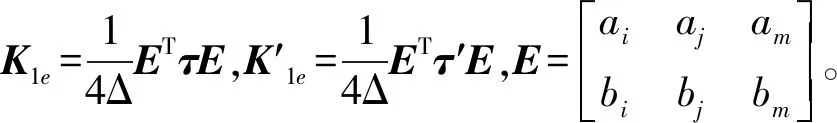
單元積分2和積分5為：

(13)

(14)

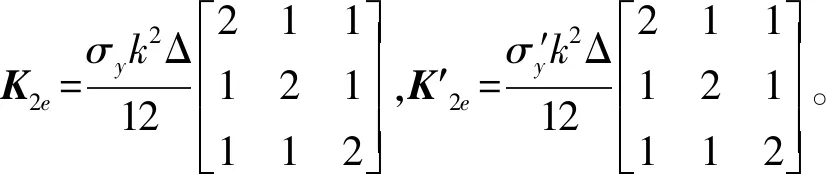
單元積分3和積分6為：

(15)

(16)

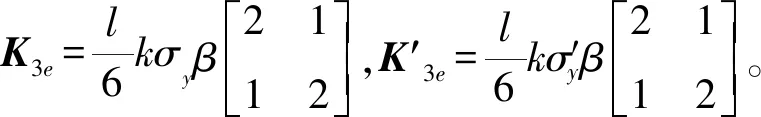
將單元矩陣添加到整體系數矩陣中的相應位置，得到式(17)。

(17)

令式(17)的變分為0，得到線性方程組(18)[3]。

(18)

解線性方程組得到波數域中異常場的電位，進行傅里葉反變換得到空間場中的異常場電位，最后加上一次場電位得到總場電位。

2.3 歐拉角的簡化

觀察式(17)和式(18)，要得到方程組還需計算波數域中的一次場電位U0，點源均勻半空間各向異性介質電位表達式為式(19)[12]。

(19)

其中B=(r-r0)T·ρ·(r-r0)，將B展開后，直接使用該表達式進行傅里葉變換較為困難，因此筆者采用簡化歐拉角的方法進行處理。假設二維構造下點源附近的介質(背景介質)電性主軸與觀測坐標系的夾角為零得到：

ρ=diag(ρx,ρy,ρz)

(20)

對式(20)進行傅里葉變換，得到傅氏空間中電位表達式為式(21)。

(21)

得到波數域中的一次場后，代入有限元公式進行計算，將角度信息也作為異常來處理，由有限元完成計算異常場的工作。

此處我們假設了背景電阻率的電性主軸與觀測坐標系的夾角α為零，所以該方法對α≠0的模型并不適合。

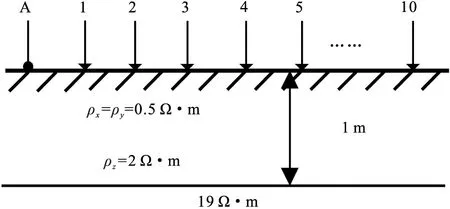
圖3 模型1：兩層含VTI介質模型

3 算例分析

3.1 兩層含垂直各向異性(VTI)介質的地電模型

設計一個兩層單界面模型，其中第一層為VTI介質，第二層為各向同性介質，模型和電極布置如圖3所示。發射電極為A點，模擬供入1A的電流，1～10為接收電極且電極之間距離為1 m。

3.1.1 算法驗證

分別使用總場法和異常場法進行模擬，選用的波數為徐世浙[3]計算的最優波數。異常場法中背景場設為ρx=ρy=0.5 Ω·m，ρz=2.0 Ω·m產生的電場，也即點源處的電阻率作為背景電阻率。將總場法與異常場法的數值模擬結果與解析解分別進行對比，如表1所示。

從模擬結果可以看出，使用異常場法精度較高，誤差均在1%以內，而總場法在點源附近誤差較大，并且整體的誤差也較異常場法較高,也證明了本文算法的正確性和準確性。

3.1.2 波數的討論

在以上計算中，如果采用宋滔等[14]計算的7點波數，總場法和異常場法的計算結果分別與解析解對比，相對誤差如表2所示。

從結果中可以看出，異常場法模擬的結果誤差非常小，但是總場法采用7點波數的模擬結果與解析解的相對誤差較大。這是因為在波數域中點源附近有限元解誤差較大，所以變換到空間域時誤差也較大；7點波數本來的精度是較高的，即如果有限元解越精確，得到空間域的電位也越準確，相反如果解的誤差較大，使用七點波數反而會使空間域的電位誤差變大。

因為在地形條件下無法使用異常場法，所以在各向異性的正演模擬中用總場法時采用5點波數；采用異常場法時選用7點波數，可以取得相對更高的精度。

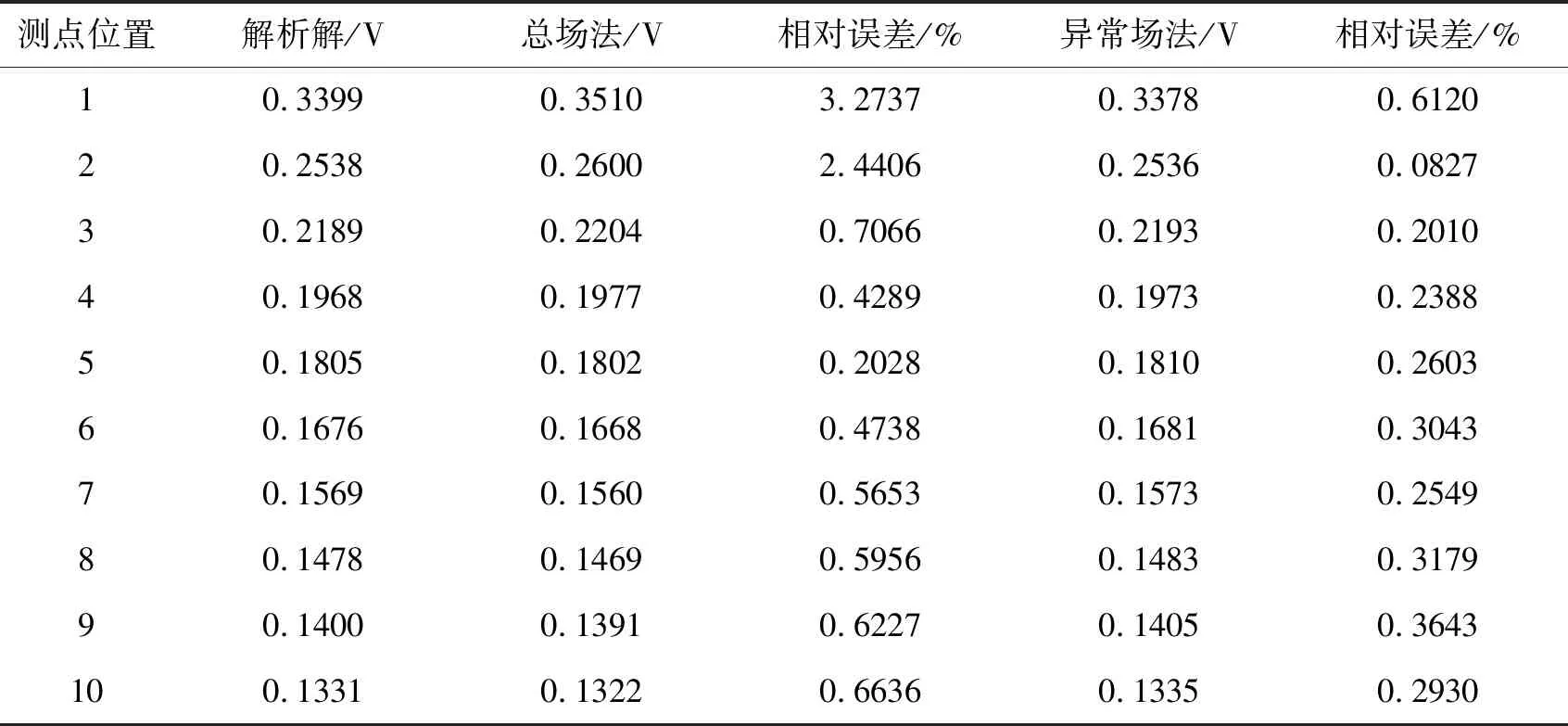
表1 數值解與解析解對比

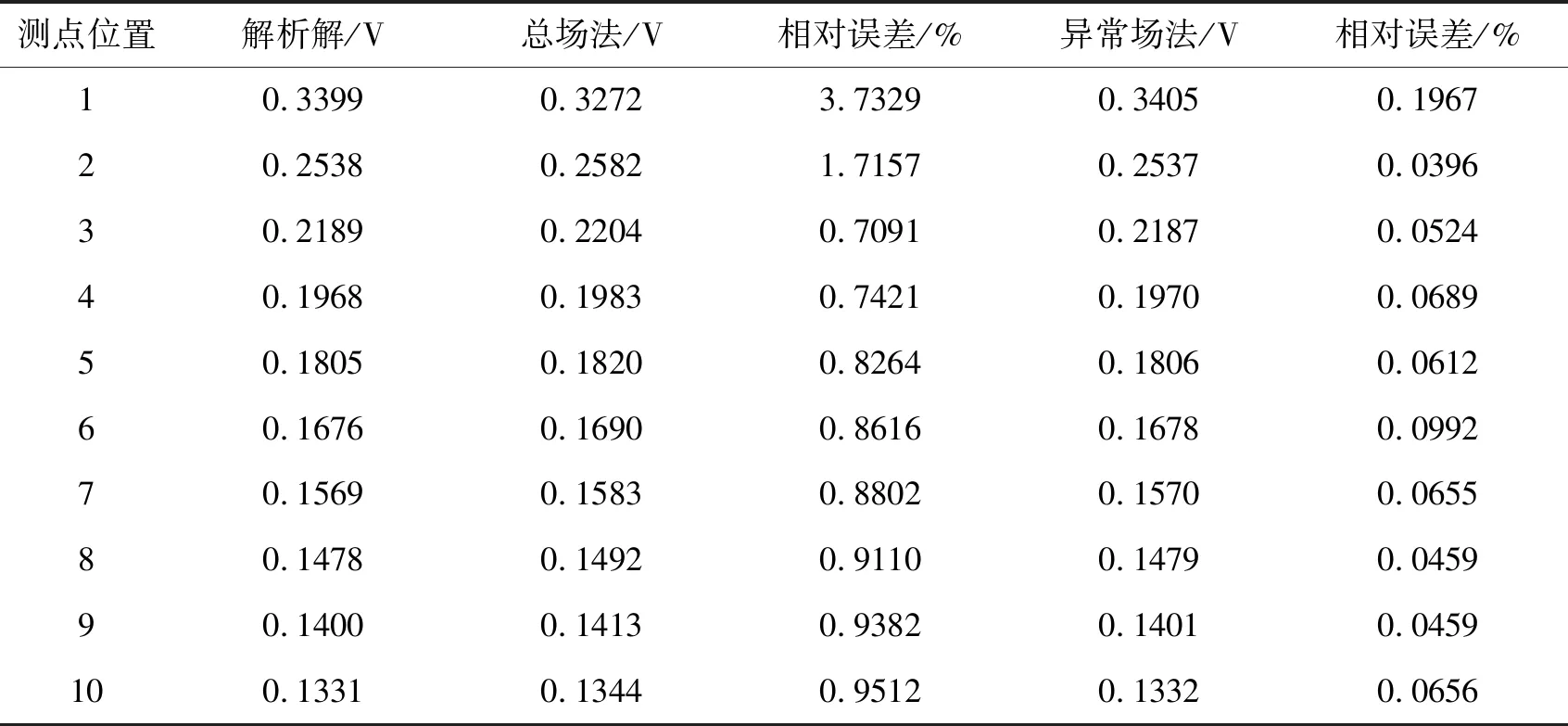
表2 采用7點波數的模擬結果對比

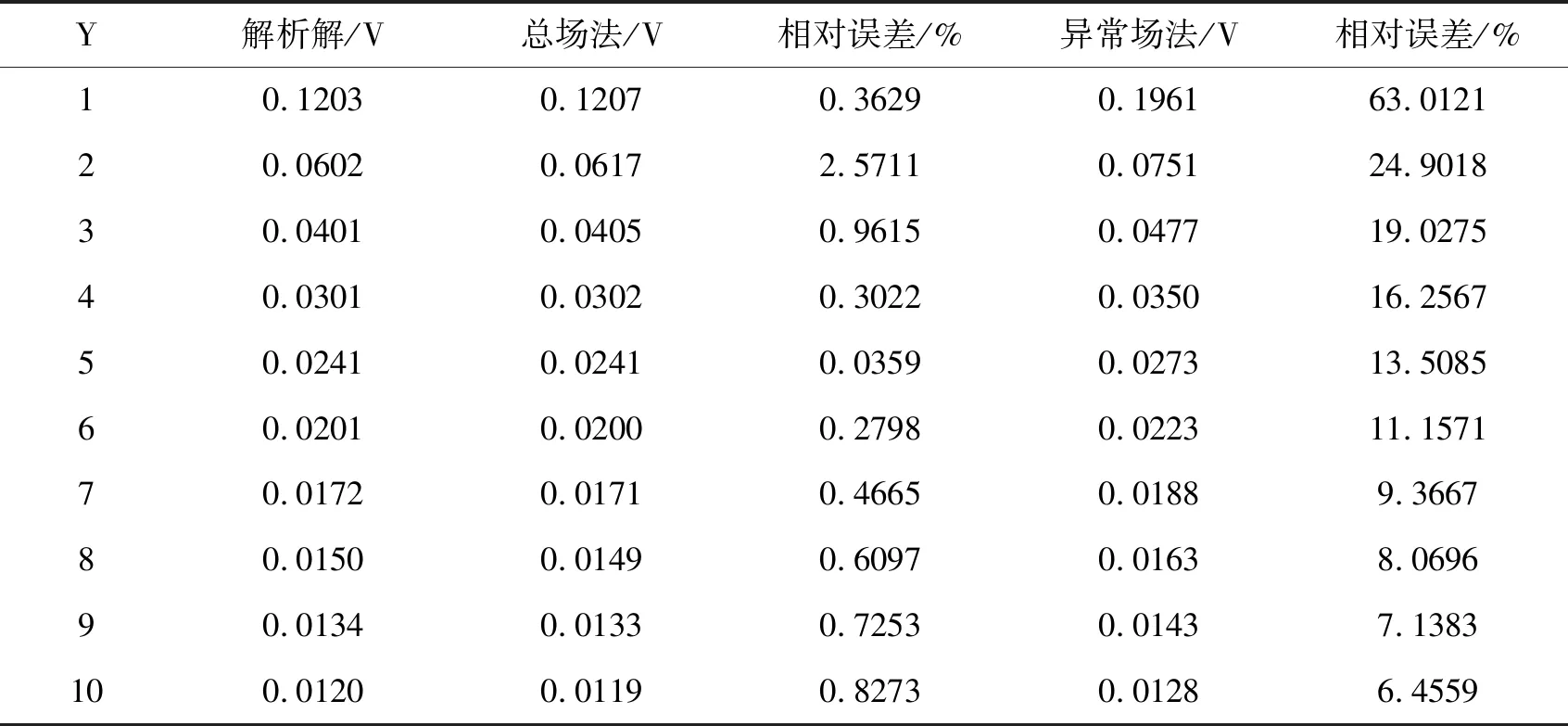
表3 TTI介質模擬結果對比

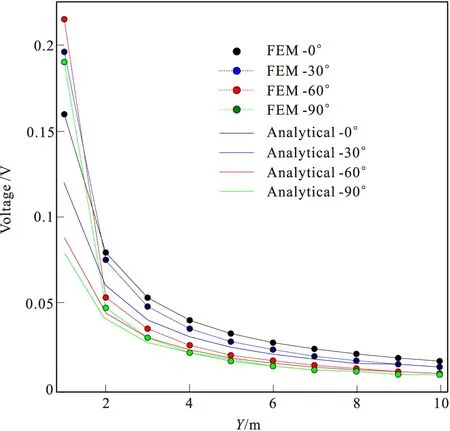
圖4 解析解與異常場法數值解曲線

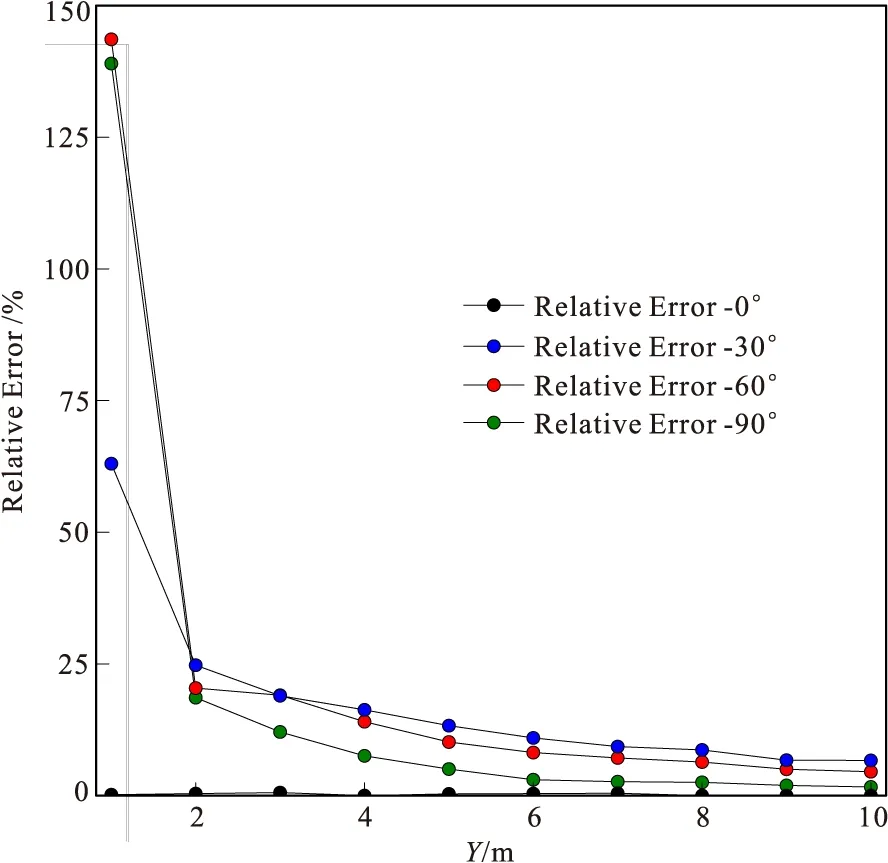
圖5 解析解與異常場法數值解相對誤差

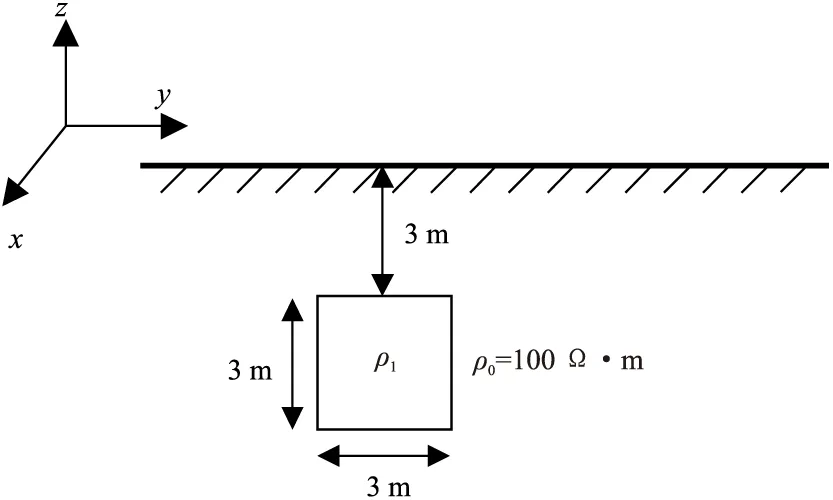
圖6 含異常體模型

3.1.3 背景電阻率的取值

采用異常場法簡化歐拉角時，假設點源附近的介質與選定坐標系的夾角為零，通過模型來計算當點源處介質為TTI時異常場的結果。

假設均勻半空間，電阻率為ρx=ρy=0.5 Ω·m，ρz=2.0 Ω·m，采用異常場法模擬α=0°、30°、60°、90°的結果，與解析解進行對比驗證文中的假設；設置電極為距離點源1 m～10 m且電極距為1 m，10個測量點。

表3給出了α=30°時，總場法與異常場法的解，以及它們與解析解的相對誤差，從表3中可以看出，總場法在臨近點源的第二個點的誤差較大，達到了2.571 1 %，在其他測點處的誤差均在1%以內；但異常場法的解誤差均較大，在源附近已經達到了63.012 1 %。因為此時背景電阻率的電性主軸與坐標系有α=30°的夾角，不滿足文中關于歐拉角的假設，所以此處采用異常場法處理的結果不準確。

設α=0°、30°、60°、90°，解析解與異常場法求解結果的曲線見圖4，以及相對誤差的曲線見圖5。

從以上模擬可以發現點源處的介質如果為TTI介質(背景介質)，只能采用總場法進行正演，文中給出的異常場法不再適用。

3.2 含異常體模型

設計如圖6所示的含異常體模型，異常體距離地面3 m，大小為3 m×3 m，背景介質為各向同性介質電阻率為ρo=100 Ω·m，在地表進行測量設置40個電極，異常體位于測量區域的中心部分。

設置三個模型，mod1異常體為各向同性電阻率為ρ=10 Ω·m，mod1異常體為各向異性電阻率為ρx=ρy=10 Ω·m，ρz=100 Ω·m，mod3異常體為各向異性，電阻率為ρx=ρy=100 Ω·m，ρz=10 Ω·m。

模擬對稱四極裝置的響應，取極距AB為3 m、7 m、11 m和21 m的視電阻率曲線進行對比，結果如圖7所示。

圖7中MD-10、MD-10-100、MD-100-10分別代表mod1、mod2和mod3。

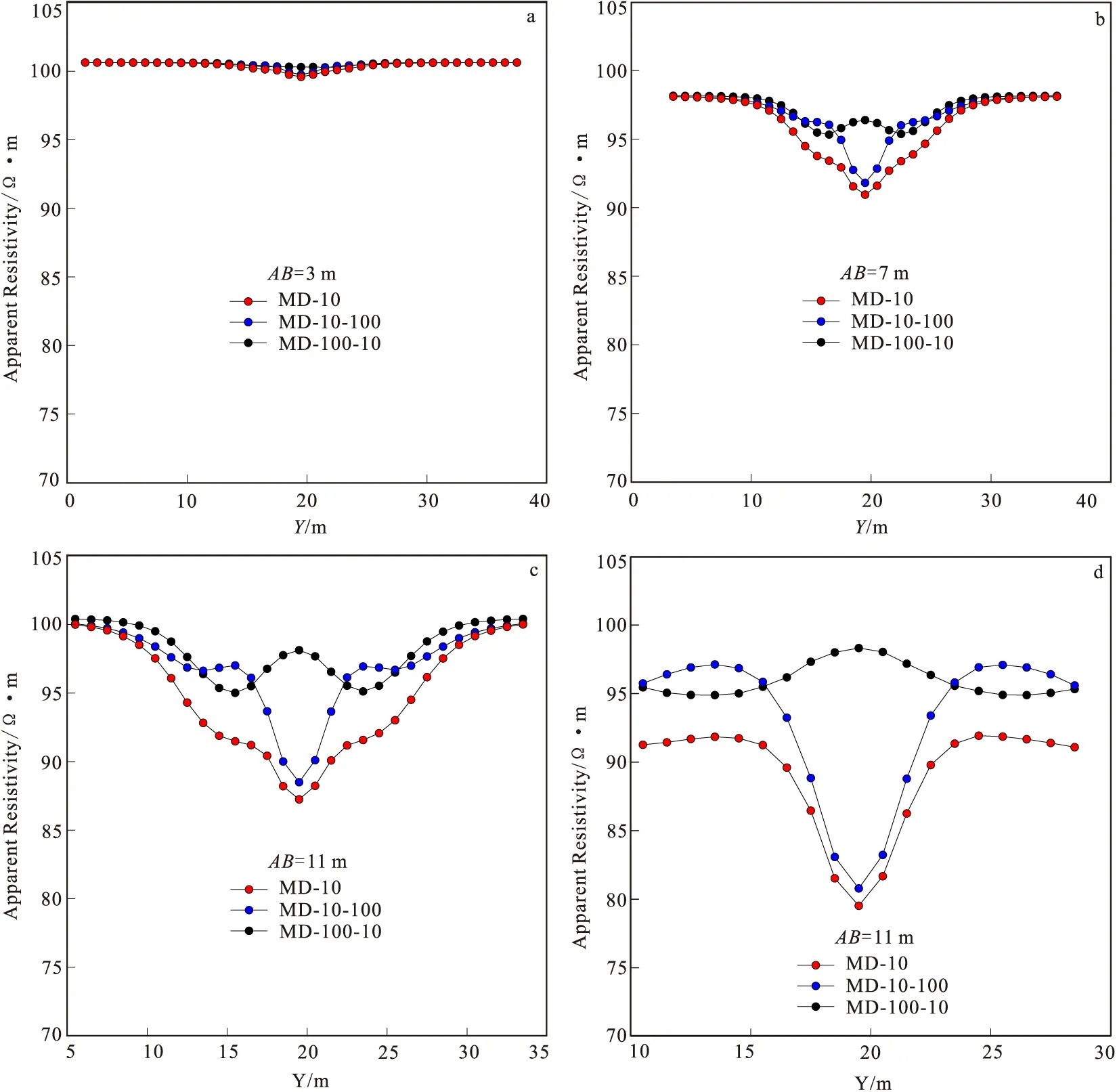
圖7 含低阻異常體模型極距為3 m、7 m、11 m和21 m模擬結果曲線圖

從圖7可以清晰得看出，當極距較小時，對稱四極法反映的是較淺介質的電性，所以三個模型的結果相近，均接近100 Ω·m，當極距變大時，受到不同異常體的影響，三個模型的視電阻率曲線出現分離。圖7中mod3在四個不同的極距下，視電阻率的值均與背景電阻率較為接近，為100 Ω·m，其異常體的橫向電阻率為100 Ω·m，縱向電阻率為10 Ω·m，而mod2模型的模擬結果與異常體為各向同性的 的模擬結果較為接近。對稱四極裝置、偶極偶極裝置以及二極裝置的響應，如圖8、圖9和圖10所示。

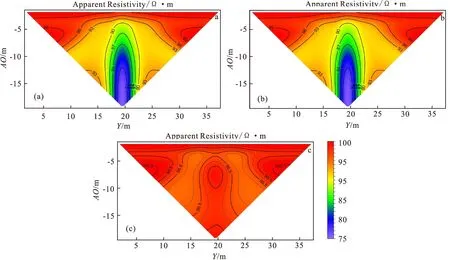
圖8 對稱四極裝置視電阻率剖面

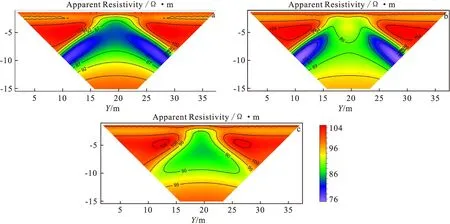
圖9 偶極偶極裝置視電阻率剖面

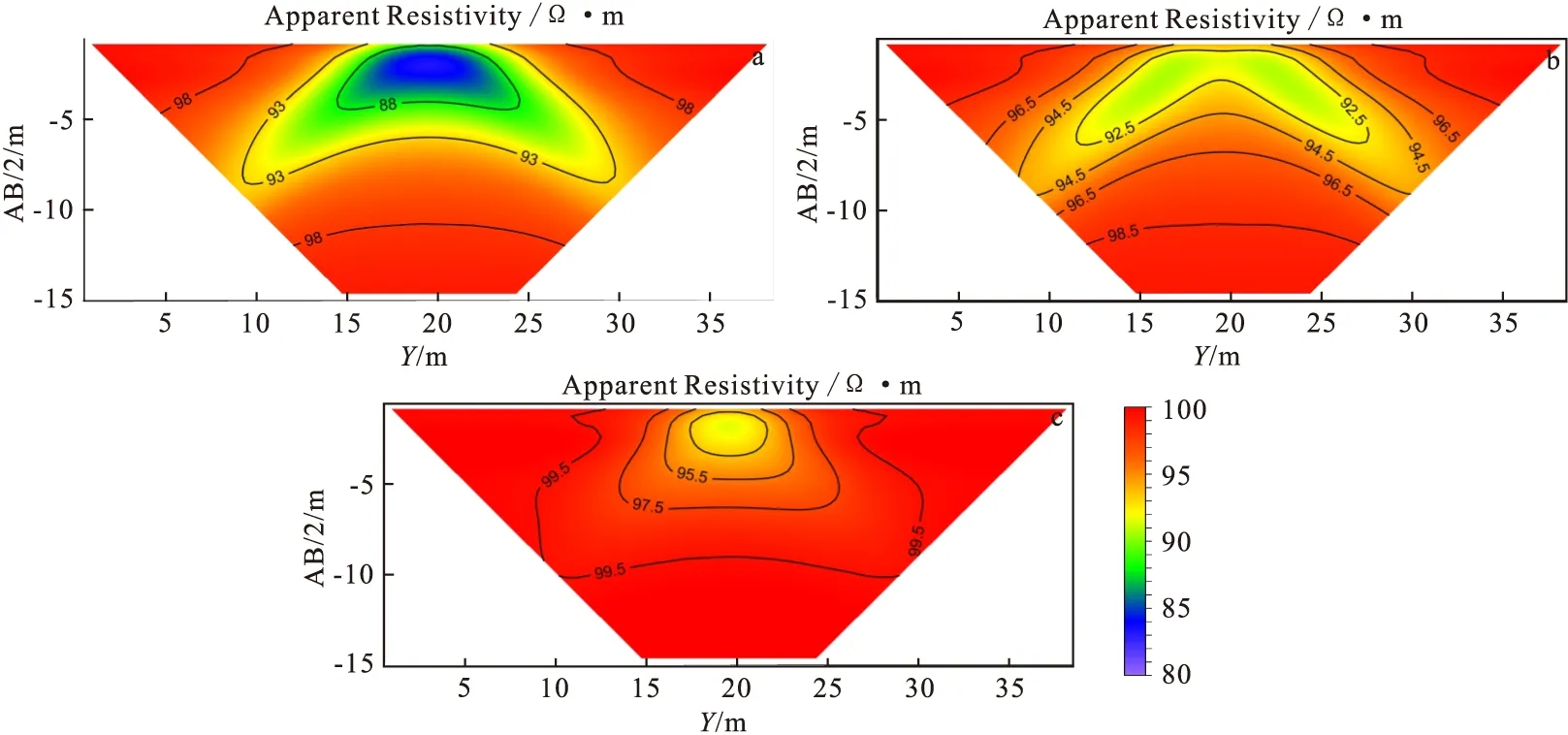
圖10 二極裝置視電阻率剖面

通過以上模擬，發現介質橫向電阻率的變化對測量的結果影響較大，而縱向電阻率對結果影響相對較小。二極和偶極偶極裝置相較于三極和對稱四極裝置，對縱向電阻率的反映更加靈敏，并且對異常的位置和形態反映也更加準確，其中偶極偶極裝置對縱向電阻率的變化最為靈敏。

4 結論

我們給出了點源2.5維各向異性異常場法的邊值問題和變分問題，并用有限元實現正演模擬。使用異常場法求解時，假設點源附近的介質為VTI介質，簡化空間電位解析解的歐拉角，使得異常場法可以進行。

通過算例分析，表明異常場法的精度更高。在模擬計算中，建議地形模型采用5點波數使用總場法，平地形模型使用異常場法7點波數，可以獲得更高的精度。

因為使用異常場法時，假設點源附近的介質為VTI介質，所以文中所提出的簡化方法并不適合點源附近的介質為TTI的情況，即介質的電性主軸與觀測坐標夾角不為0時，該方法并不適合。

通過模擬，發現對于二維介質，直流電阻率法對橫向電阻率的變化更為靈敏，而縱向電阻率對結果影響相對較小。