采用不同模擬方法的預制拼裝橋墩擬靜力加載模擬對比
孟慶一,李 剛
(1.青島理工大學 土木工程學院 青島市 266033; 2.濱化集團股份有限公司 濱州市 256600)
0 引言
隨著我國基礎設施建設行業的快速發展,橋梁工程開始向著快速、綠色、低能耗、低成本的方向發展。預制拼裝橋墩與整體現澆橋墩相比具有施工工期短、對周圍環境影響小、不阻礙交通等優勢[1-2],已經成為未來橋梁下部結構的應用趨勢,國內外已有很多橋梁應用預制拼裝橋墩作為下部結構;例如國外的佛羅里達七英里大橋、德克薩斯州183高速公路高架橋;我國的東海大橋、杭州灣大橋、港珠澳大橋等[3]。
目前,針對預制拼裝橋墩數值模擬的方法主要有三種:纖維模型法、實體模型法、集中塑性鉸模型法。葛繼平[4]等基于OpenSEES軟件進行過橋墩纖維模型法的模擬;Amini[5]、包龍生[6]等基于ABAQUS軟件進行過橋墩實體模型法的模擬;葛繼平[7]等基于OpenSEES軟件進行過橋墩集中塑性鉸模型法的模擬。以上各模擬結果均有試驗結果作為對比,證明三種模擬方法均可以準確模擬預制拼裝橋墩的力學性能,但三種分析方法在一起的對比工作進行的仍較少。
本研究基于現研究階段三種預制拼裝橋墩最常用的數值模擬方法:纖維模型法、實體模型法、集中塑性鉸模型法,建立三種預制拼裝橋墩有限元分析模型,進行擬靜力加載模擬,采用滯回性能、骨架曲線、累積耗能、剛度退化作為模擬對比指標,對三種分析模型的模擬效果做出評價,為預制拼裝橋墩的模擬提供參考。
1 預制拼裝橋墩有限元模擬方法
1.1 纖維模型法
纖維模型分析法是根據橋墩截面的材料組成和位置,把橋墩的截面材料分成若干種類的纖維單元,如圖1(a)所示,在計算時,通過合理劃分單元上的積分點數目,可以大大提高計算速度和準確性,如圖1(b)。
利用OpenSEES軟件建立節段預制拼裝橋墩纖維模型如圖2所示。纖維模型節段混凝土采用Concrete01本構,節段鋼筋采用Steel02本構模擬;普通節段采用非線性梁柱單元模擬,預應力鋼絞線采用桁架單元模擬,墩頂和墩底節點約束三個方向自由度模擬鋼絞線的錨固,中間節點與混凝土節點一一對應,約束水平兩個方向自由度,模擬鋼絞線在波紋管中的擺動,初始預應力采用初應變的形式施加;節段與節段接縫區域采用與接縫等長的接縫單元模擬,接縫單元中混凝土采用Concrete02本構不考慮受拉(受拉強度為0),采用墩身約束混凝土本構,應變取相鄰上方墩身約束混凝土的極限應變;橋墩自重采用集中質量方法在墩頂加載,總軸壓比為0.1。在橋墩底部使用零長度單元配合BondSP01材料(如圖3所示)來模擬鋼筋的粘結滑移現象。
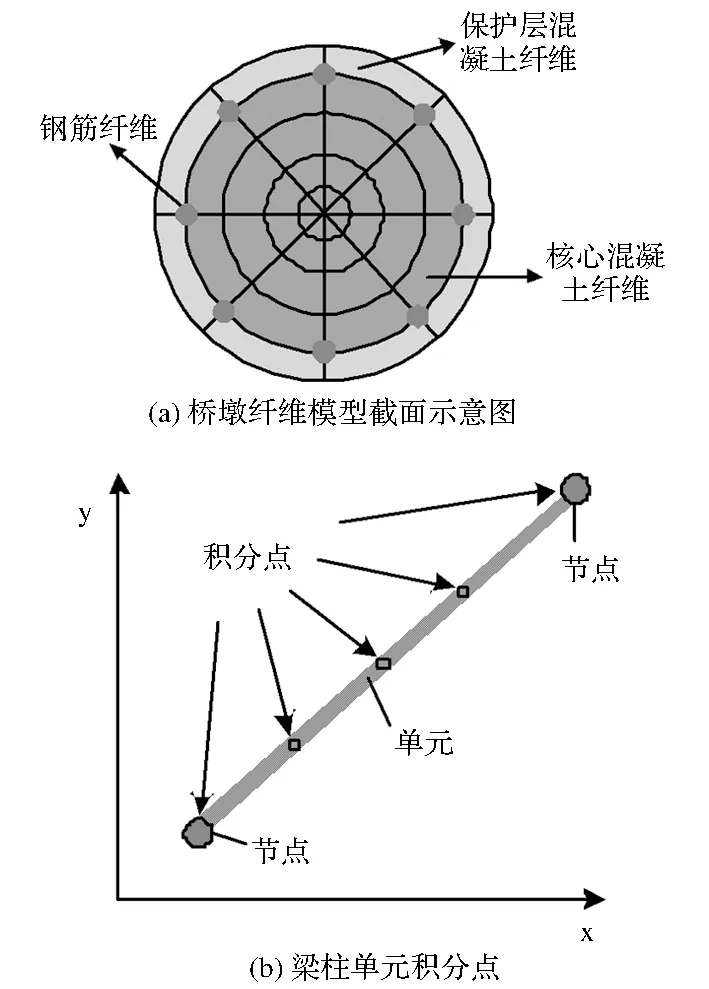
圖1 橋墩纖維截面和梁柱單元積分點
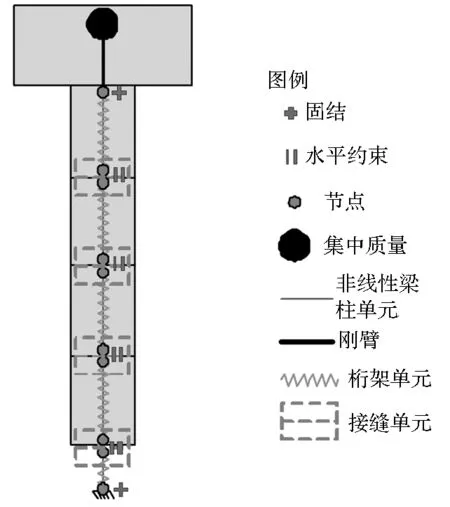
圖2 預制拼裝橋墩纖維模型
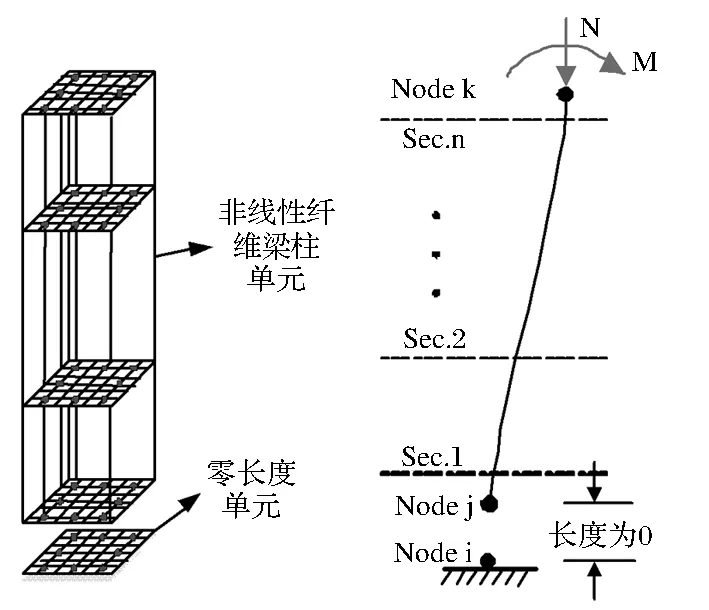
圖3 零長度單元模擬粘結滑移
1.2 實體模型法
實體單元分析法為依照橋墩的實際尺寸和構造建立橋墩有限元實體分析模型(包括混凝土和鋼筋),在分析時可充分考慮橋墩混凝土的塑性應變;縱向鋼筋和預應力鋼筋的應力變化,可操作性強。但也常常因為過于繁瑣的接觸計算而導致模型收斂困難,計算時應合理設置計算參數和接觸約束選項。
利用ABAQUS軟件建立預制拼裝橋墩實體模型如圖4所示。實體模型混凝土采用損傷塑性模型,鋼筋采用雙折線模型;節段縱筋和箍筋合成為鋼筋籠,內置于模型中;預應力鋼絞線分別嵌入在墩頂和墩底的混凝土中,采用降溫的方式施加初始預應力;對于模擬施加預應力大小(與溫度變化有關)的計算式為:
P=alΔtEsAs
(1)
式中:P為預應力鋼絞線的預應力;al為所設置預應力鋼絞線的膨脹系數,本模擬取值0.0001;Δt為溫度場溫度變化;Es為預應力鋼絞線的彈性模量;As為預應力鋼絞線的截面面積。
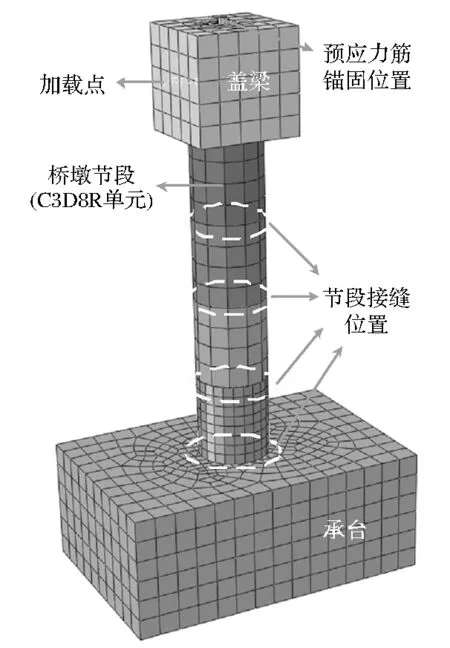
圖4 預制拼裝橋墩實體模型
混凝土選用C3D8R六面體單元模擬,節段鋼筋籠和預應力鋼絞線均選用T3D2梁單元模擬。節段與節段之間的接觸,切向定義面與面接觸,摩擦系數取0.4,法向定義為硬接觸。橋墩自重采用集中質量方法在墩頂加載,總軸壓比為0.1。
1.3 集中塑性鉸模型法
橋墩在較小的水平地震力作用下保持彈性工作狀態,在受到較大水平的地震力作用時,橋墩由起初的彈性狀態進入塑性狀態,產生非線性形變,橋墩墩底會形成塑性鉸,如圖5(a)所示,墩底塑性鉸范圍內截面曲率保持一致,其長度被稱為塑性鉸長度,利用曲率乘以塑性鉸長度就可將其轉換為集中轉動彈簧模型,如圖5(b)所示。該彈簧的性能控制參數需要根據橋墩集中塑性鉸長度、截面彎矩曲率關系以及橋墩自身的加卸載關系來確定。
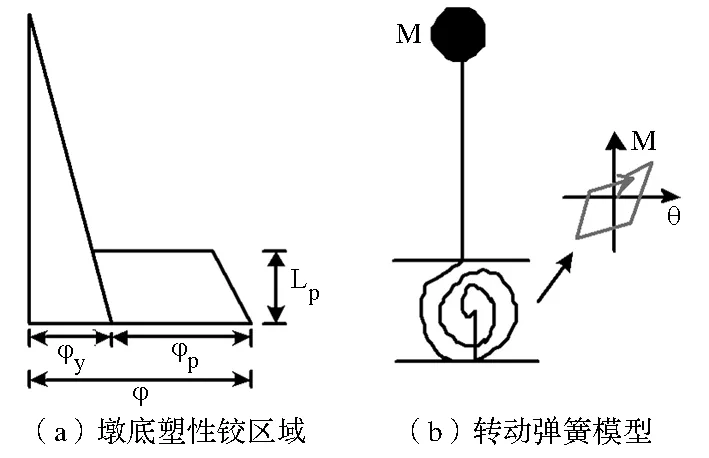
圖5 預制拼裝橋墩底塑性鉸
本文采用Priestley等人提出的公式計算塑性鉸長度:
對于預應力混凝土結構(包括預制拼裝混凝土結構),塑性鉸長度計算公式為:Lp=D/2
(2)
式中:Lp為墩底塑性鉸長度;D為加載方向寬度。
對于普通鋼筋混凝土結構,塑性鉸長度計算公式為:
Lp=0.08L+0.022fyedbl
(3)
式中:L為橋墩墩高;fye為縱筋屈服應力;dbl為縱筋直徑。
橋墩截面的彎矩-曲率采用XTRACT程序進行計算,其中需要考慮預應力筋長度伸長而產生的應變。
利用OpenSEES軟件建立預制拼裝橋墩的集中塑性鉸模型如圖6所示。橋墩上部采用剛性梁單元模擬,在墩底加入零長度單元配合PinChing4材料模擬橋墩的非線性行為和橋墩的彎矩-曲率計算關系。橋墩自重采用集中質量方法在墩頂加載,軸壓比為0.1。
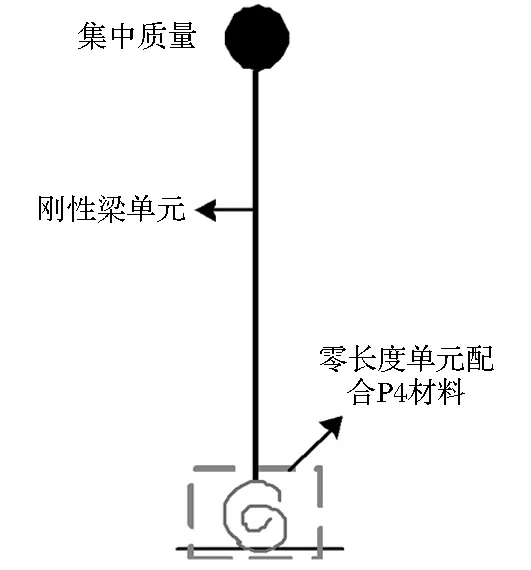
圖6 預制拼裝橋墩集中塑性鉸模型
PinChing4材料的本構關系如圖7所示,此材料可以通過定義骨架曲線上12個關鍵浮點,模擬材料的非線性行為和加卸載關系。表1給出了PinChing4材料經過計算之后的模型加卸載參數值。
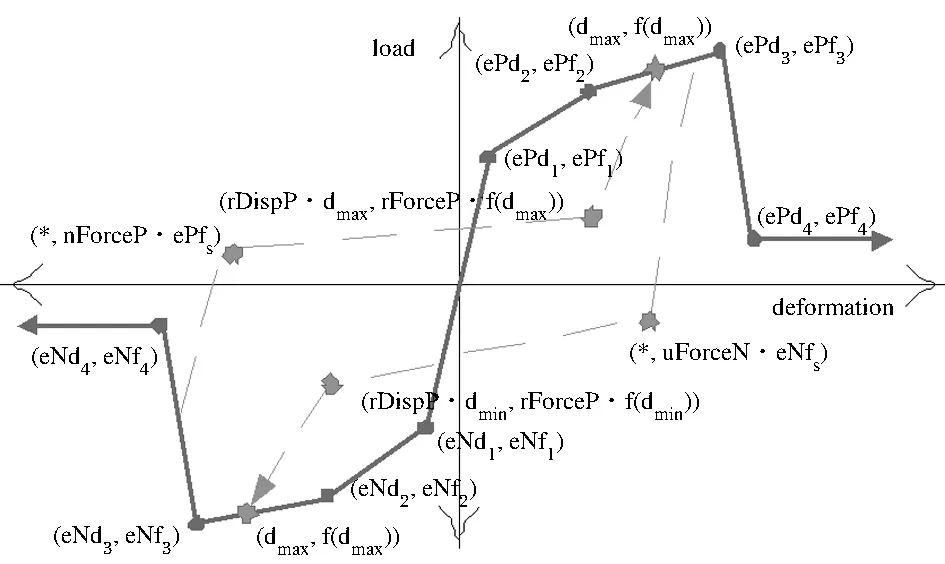
圖7 PinChing4材料本構模型

表1 模型加卸載參數值
2 預制拼裝橋墩數值模擬
2.1 算例橋墩的選取
選取文獻[8]中的預制拼裝橋墩試件2作為本次模擬計算的算例橋墩,試件2橋墩實際構造如圖8所示,混凝土、鋼筋和預應力鋼筋相關材料參數見表2。
2.2 加載制度
文獻[8]中試驗的擬靜力加載采用位移控制方式,側移幅值依次為0.1%、0.2%、0.3%、0.5%、0.75%、1%、1.5%、2%、2.5%、3%、3.5%、4%、
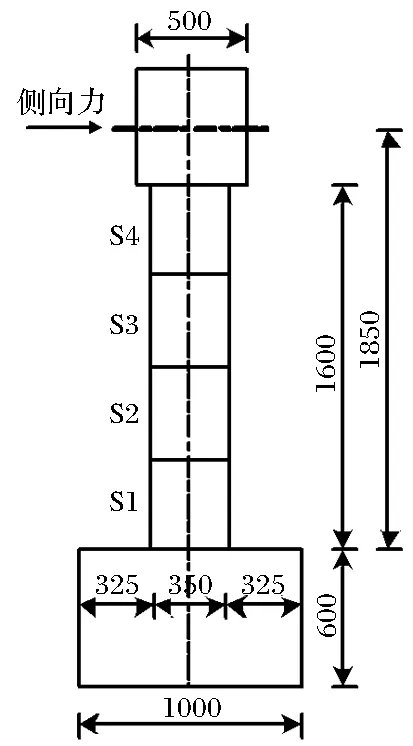
圖8 預制拼裝橋墩試件2構造圖
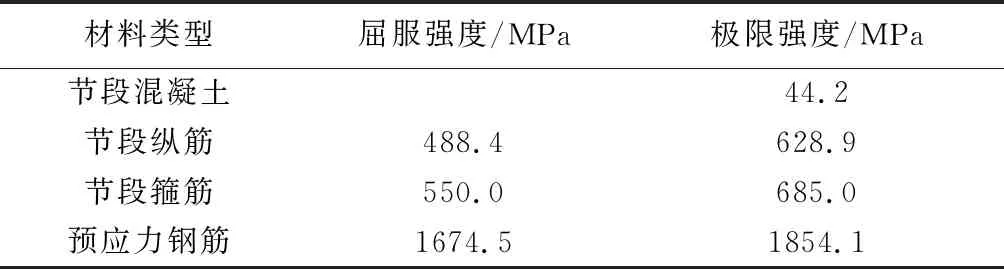
表2 試件2混凝土和鋼筋材料參數
4.5%、5%、6%、7%,每級2次循環加載。本文有限元分析擬靜力加載采用相同的加載幅值,為了使分析結果更加清晰準確,每級加載由2次減為1次,加載制度如圖9所示。
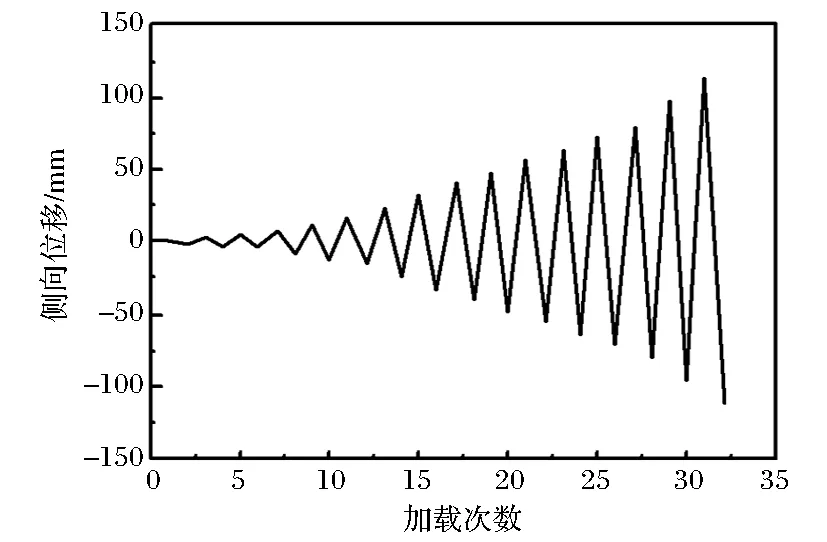
圖9 數值分析加載制度
3 結果分析
3.1 滯回曲線
經過擬靜力加載分析后,輸出不同橋墩模型的墩頂水平位移和墩底剪力,繪制出不同模型的水平力-位移滯回曲線如圖10所示,并將3組模型滯回曲線進行對比,如圖11所示。
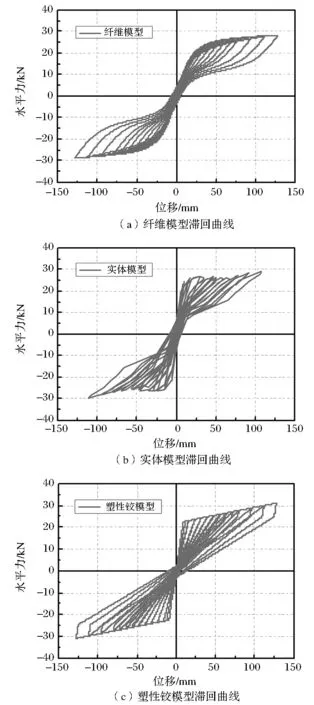
圖10 不同模型滯回曲線
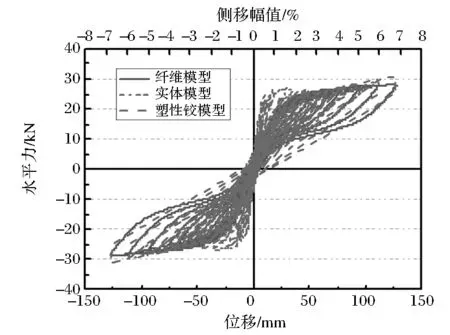
圖11 不同模型滯回曲線比較
從圖10可以看出,預制拼裝橋墩因預應力筋提供了較強的自復位能力,所以具有較小的殘余位移和耗能,滯回曲線呈雙旗型。三種分析模型對預制拼裝橋墩滯回性能的模擬效果各不相同,每種模擬方法均有自己優勢和不足。由圖11可知,實體模型計算最為精確,滯回環捏縮程度最大,更加符合此類型橋墩的實際試驗滯回性能,模型加卸載關系均與實際較為接近,而纖維模型和塑性鉸模型滯回環相對實體模型更為飽滿,滯回耗能更大,可能會高估橋墩的實際耗能能力。塑性鉸模型滯回曲線平直,模擬非線性的能力較弱。墩身若干節段通過預應力鋼筋牽拉成為整體的預制拼裝橋墩具有較大的剛度,這點的模擬上實體模型和塑性鉸模型具有更大的初始剛度和卸載剛度,與實際更為符合。三種模型加載后期均未表現出剛度和強度的下降。
3.2 骨架曲線
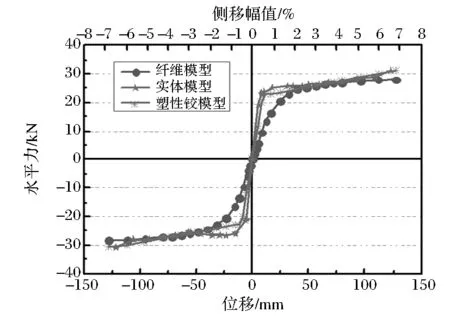
圖12 不同模型骨架曲線比較
由圖12可知,三種模擬方法模擬的橋墩模型骨架曲線各有不同,各模型加載后期均沒有出現明顯強度的下降,說明橋墩始終保持良好變形能力,加載后期并未出現較大的損傷;各模型具有幾乎相同的極限承載力,極限承載力分別為29.5kN、31.02kN、31.03kN。實體模型與塑性鉸模型初始剛度吻合較好,均大于纖維模型;實體模型在加載幅值達到2%后,有小幅的強度下降。
3.3 累積耗能
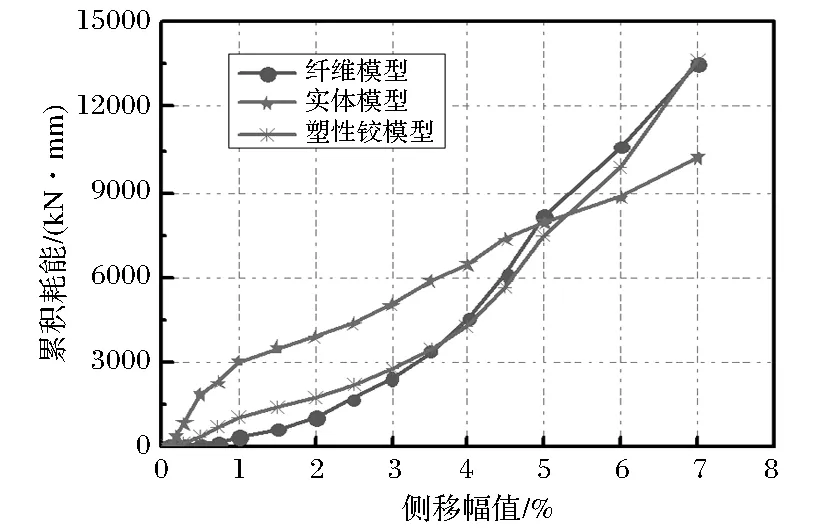
圖13 不同模型累積耗能比較
由圖13可知,加載前期實體模型累積耗能增長較快,在側移幅值為5%之前擁有最大的累積耗能,但側移幅值大于5%之后纖維模型和塑性鉸模型累積耗能超過實體模型;側移幅值為7%時纖維模型、實體模型、塑性鉸模型累積耗能分別為13516.42kN·mm、10226.9kN·mm、13659.03kN·mm。
3.4 剛度退化
繪制出不同橋墩模型的曲線如圖14所示,為橋墩水平力-位移曲線在原點處的切線斜率,等效剛度又被稱為割線剛度,為橋墩水平力-位移曲線上任一點(除原點)處切線的斜率。
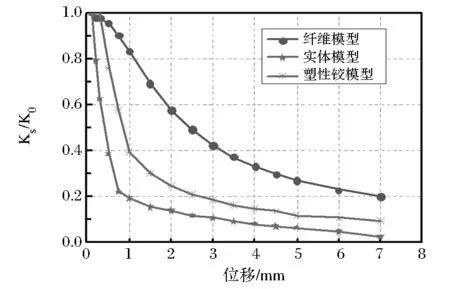
圖14 不同模型剛度比較
從圖14可以看出,各模型在加載初期剛度下降均較快,加載后期剛度趨于平緩,構件損傷發展變緩。纖維模型具有最大的值,其次是塑性鉸模型,最小的是實體模型;說明實體模型在模擬橋墩損傷累積方面具有更好的效果。因為具有較大的初始剛度,使得實體模型和塑性鉸模型橋墩剛度退化速度要明顯大于纖維模型。纖維模型對橋墩受到損傷后剛度退化的模擬敏感程度偏低。
4 結論
基于纖維模型法、實體單元法、集中塑性鉸法三種不同的模擬方法,利用OpenSEES和ABAQUS有限元分析軟件,分別建立預制拼裝橋墩的三種有限元模型,對比三種有限元模型的計算結果得出結論如下:
(1)三種分析模型模擬預制拼裝橋墩的滯回性能均存在優劣勢,實體模型滯回性能與試驗結果最為接近,實體模型和纖維模型可以更好地模擬預制拼裝橋墩非線性能力,塑性鉸模型模擬非線性能力較弱。
(2)三種分析模型模擬橋墩極限承載力和剛度方面能力相當,當橋墩發生大的側移幅值時纖維模型和塑性鉸模型耗能能力接近,均要大于實體模型。
(3)實體模型在模擬預制拼裝橋墩損傷方面具有更好的效果,纖維模型對橋墩損傷后剛度退化的模擬敏感程度偏低。
(4)為了更準確地評價三種模擬方法模型預制拼裝橋墩的優劣程度,仍需要比較更多的參數指標。

