基于剩余能量的認知無線傳感器網絡頻譜分配*

宋婷婷,張達敏,陳忠云,徐 航

(貴州大學大數據與信息工程學院,貴陽 550025)

無線傳感器網絡由大量分布在一定地理位置上的功率受限的傳感器節點組成 用于監視和報告某些特定的物理特征[1]。無線傳感器網絡(Wireless Sensor Networks,WSNs)使用未經許可的工業、科學和醫學(ISM)波段進行傳輸。然而,隨著這些網絡的使用和需求的增加,目前可用的ISM頻段不足以滿足它們的傳輸需求,將無線傳感器節點結合認知無線電(Cognitive Radio,CR)技術構成的認知無線傳感器網絡(Cognitive Wireless Sensor Networks,CRSNs)[2]讓傳感器節點作為次用戶(認知用戶)動態地和機會地訪問主用戶(授權用戶)頻帶中的頻譜漏洞。

CRSNs的信道分配方式大概分為集中式和分布式兩種。在集中式分配方式中[3],一個中心實體(例如,基站或專用協調器)檢測和識別頻譜機會,并根據預定義的策略將識別的頻譜分配給次用戶。當接收到傳輸請求時,中心實體會將頻譜分配的結果傳播到傳感器群中,這將帶來消息交換的開銷。在分布式方案中,傳感器相互競爭訪問頻譜資源。因此,每個傳感器都有能力檢測頻譜機會,并確定最佳策略,以最大限度地提高其效益,每個節點只與離它最近的或同一簇內的節點共享頻譜感知信息。

由于CRSNs中的傳感器節點依賴于供電能力有限的電源。因此,傳感器節點之間進行動態、高效的頻譜分配方案對于優化網絡中各個節點的能源消耗、最大限度地延長網絡生存期是非常必要的[4-7]。本文構造了一種認知無線傳感器網絡的能耗和信道狀態模型,以最大化網絡剩余能量為優化目標,對傳統的灰狼算法的位置向量更新進行改進。針對CRSNs,通過引入動態轉換函數,提出了一種改進的基于二進制灰狼優化算法(Improved Binary Gray Wolf Optimization Algorithm,IBGWO)的頻譜分配方案。通過實驗仿真比較分析,該方案能快速收斂達到全局最優,證明了 IBGWO 算法解決該問題的有效性和優越性。

1 系統模型及問題描述

1.1 網絡模型

本文的認知無線傳感器網絡是星形拓撲結構,含多個子簇。圖1是CRSNs網絡模型。每個子簇包含一個簇頭和若干簇成員,簇頭和簇成員都是傳感器節點且為次用戶,一個簇中的次用戶都只與其簇頭通信。主用戶分布于CRSNs網絡中,使用固定的授權頻譜,次用戶通過認知無線網絡的頻譜感知技術感知當前主用戶的可用頻譜,進行機會式接入使用。但若主用戶需要占用該信道,認知用戶則必須退出當前信道,認知無線傳感器網絡模型如圖1所示。

圖1 認知無線傳感器網絡模型

圖2 雙狀態馬爾科夫過程

1.2 主用戶行為及能量消耗建模

CRSNs網絡中主用戶行為可以使用雙狀態馬爾科夫過程來建模,以獲取當前狀態對先前狀態的依賴關系。各信道狀態根據主用戶信號的存在與否分為占用和空閑兩種,該過程可由圖2表示。

這個過程獨立于信道之間。對于第j個信道,Pj表示在當前時隙空閑的情況下,信道在下一個時隙被占用的概率。同樣,qj表示在當前時隙中信道j被占用的情況下,在下一個時隙中空閑的概率。經推導可得信道j空閑概率由式(1)表示:

(1)

假設一個數據幀的發送占據L個時隙。根據馬爾可夫模型,傳感器成功傳輸一個數據幀的概率等于所選信道j連續L個時隙處于空閑狀態的概率:

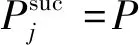
=(1-pj)L

(2)

(3)

假設一個簇中部署了I個傳感器,每個傳感器攜帶一個具有相同初始能量的不可充電電池。通信信道可以看作是一個簡單的路徑損耗模型,其中忽略了衰落和多徑效應。數據傳輸中的能量消耗為Ecir+εd2,其中Ecir為射頻電路的能量消耗,ε為接收機所需的放大器能量。d為簇成員傳感器與簇頭之間的距離。如果傳感器i傳輸l個時隙,總能耗為Ei(l):

(4)

根據上述公式,可以得到傳感器i在j信道上傳輸的統計期望能耗:

(5)

(6)

1.3 信道矩陣模型

本文的認知無線傳感器網絡的頻譜分配模型可以抽象為基于圖論著色理論的頻譜分配模型[8-9],把頻譜資源分成獨立的可用信道,次用戶機會接入主用戶空閑的可用頻譜。假設次用戶數為I,可用頻譜數為J,則相關矩陣定義如下:

①可用矩陣S={si,j|si,j∈{0,1}}I×J表示傳感器節點i是否可以使用頻譜j,si,j=1表示可以,si,j=0表示不可以。

②干擾矩陣C={ci,k,j|ci,k,j∈{0,1}}I×I×J表示不同的傳感器節點i和k在使用同一頻譜j時是否會存在干擾。ci,k,j=1表示存在干擾,ci,k,j=0表示不存在。

③信道分配矩陣A={ai,j|ai,j∈{0,1}}I×J表示信道j是否可以分配給傳感器節點i且不會對其他用戶產生影響。ai,j=1表示可以,ai,j=0表示不可以。矩陣同時滿足矩陣L和干擾矩陣C的條件為:

ai,jak,j=0∩ci,k,j=1 ?1≤i,k≤I,1≤j≤J

(7)

④剩余能量矩陣B={bi,j}I×J表示傳感器節點i選擇信道j傳輸數據,i節點的剩余能量。

整個網絡的剩余能量最大化對網絡的壽命最大化至關重要,因此由信道分配矩陣和剩余能量矩陣,可以得出頻譜分配完成后網絡中每個次用戶傳感器節點的剩余能量為Ri,則基于最大化網絡剩余能量的信道分配可表示為:

(8)

為了衡量每次頻譜分配結果的公平性,即網絡中各次用戶的剩余能量是否均衡,可以用網絡的比例公平性函數Ffairness表示:

(9)

2 IBGWO算法及CRSNs頻譜分配方案

灰狼優化算法(Gray Wolf Optimizer,GWO)屬于生物啟發式搜索算法,它模擬了灰狼群的特定等級和狩獵行為[9],具有調節參數少、編程易實現等特點,通常用在連續空間尋找最優解。而頻譜分配屬于解決離散空間組合優化問題,本文將定義新的轉換函數進行狼群在二進制空間里的位置更新,同時對收斂因子和位置更新公式進行改進,得到基于 IBGWO 的認知無線傳感器網頻譜分配策略通過尋求最大的剩余能量,進而得到網絡性能最優的頻譜分配策略。

2.1 基本灰狼優化算法

在GWO算法中,每只灰狼代表種群的1個候選解,其中,最佳候選解稱為α,第二最佳候選解稱為β,第三最佳候選解δ,其余候選解稱為ω。在捕食行為中,在已知獵物位置情況下,先包圍獵物,則當前灰狼的位置更新公式如式(11):

D=|KXP(t)-X(t)|

(10)

X(t+1)=XP(t)-GD

(11)

式中:t表示迭代次數,G和K為系數向量,XP表示獵物位置,X表示在獵物周圍的灰狼位置。G和K的表示為

G=2ar1-a

(12)

K=2r2

(13)

(14)

r1和r2為在[0,1]區間的隨機向量,a是收斂因子,隨著迭代次數從2線性遞減為0。在捕食過程中,灰狼群能夠識別獵物的位置并對其進行包圍,假設當前狀態中的α、β、δ對獵物的潛在位置有更好的感知力,其他搜索代理(包括ω)根據α、β、δ的位置更新其位置。所以下一代灰狼群位置的更新如式(15)所示:

(15)

Dα=|KXα-X|

Dβ=|KXβ-X|

Dσ=|KXσ-X|

(16)

X1=Xα-G1Dα

X2=Xβ-G2Dβ

X3=Xσ-G3Dσ

(17)

2.2 改進的二進制灰狼優化算法(IBGWO)

2.2.1 動態轉換函數

不同于GWO算法,本文中灰狼的位置更新是在二進制搜索空間進行的。目前已知的灰狼算法都是使用原始sigmoid函數作為轉換函數將位置映射到0～1之間[10-12],確定當前位置最終取值。一般來說,在運行的早期階段,優化算法應該更注重探索能力,避免陷入局部最優,但是在運行的后期階段算法則需注重開發能力,以提高求解精度。基于此本文提出了一種動態轉換函數,將灰狼的位置更新采用具有概率性質的方程,決定位置為0或1的概率,確定當前位置最終取值,能動態調節算法中探索與開發能力的平衡,該轉換函數如式(18)所示:

(18)

(19)

(20)

2.2.2 基于比例權重的位置更新

基本灰狼算法通過計算α、β、δ位置的平均值進行位置更新,但這樣沒有體現這三只狼在捕食過程中的貢獻程度及α狼作為主要領導者和適應度最高的個體在決策時的重要性。本文提出由α、β、δ的適應度值之間的比例構成2個權值因子,使α狼在狩獵過程中占有更大的權重,動態調整算法的位置向量更新,其表達式為:

w1=fa/fδw2=fβ/fδ

(21)

(22)

式中:fa、fβ、fδ分別為α、β、δ狼的適應度值。

2.2.3 算法性能測試

為了驗證算法性能的有效性,采用4個測試函數,取30次獨立優化結果,將IBGWO算法與采用原始sigmoid函數作為轉換函數的GWO算法、傳統的二進制粒子群算法BPSO和遺傳算法GA作比較。表1為測試函數列表,表2為優化結果。

表1 測試函數列表

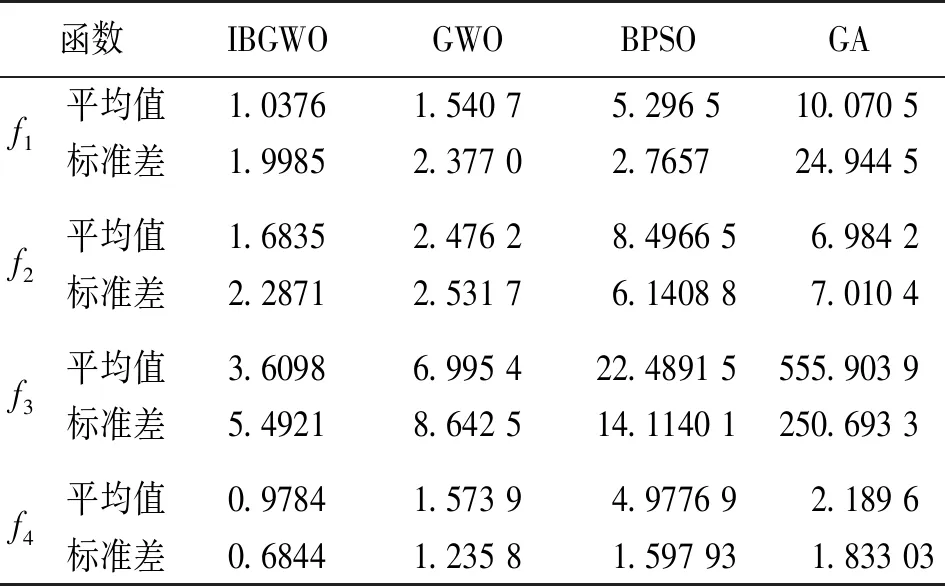
表2 算法優化結果

單峰測試函數只有一個極值,通過其結果可以更好地分析算法的全局搜索能力。多峰測試函數具有多個極值,對多峰測試函數的優化可以分析出算法跳出局部最優的能力。通過表2可知,IBGWO算法與其他三種算法相比,對于單峰測試函數和多峰測試函數,IBGWO算法的平均值和標準差都小于其他算法,因此具有更好的尋優能力和穩定性。

2.3 頻譜分配方案

本文提出的基于IBGWO的CRSNs頻譜分配方案中,每只灰狼位置對應一種頻譜分配方案。因此,頻譜分配問題的最終求解目標即為最大化剩余能量的無干擾信道分配矩陣A。因為可用矩陣S和信道分配矩陣A之間的約束關系,所以可用矩陣S中的零元素在位置上對應矩陣A的0元素,即當前通信環境下頻譜j不能分配給用戶i使用,即Si,j=0,從而ai,j只能為0。解只記錄與可用矩陣S中值為1的元素位置對應的分配矩陣A中的元素值,所以解的編碼長度D由矩陣S中1個數決定,其計算公式如式(23):

(23)

基于IBGWO的CRSNs頻譜分配方案具體實現流程如下:

①生成矩陣:由CRSNs網絡拓撲結構得到可用矩陣S,剩余能量矩陣B以及干擾矩陣C。

②初始化參數:隨機產生初始灰狼種群。

③根據適應度函數計算個體適應度值,并對適應度值進行排序,記錄適應度排前三的個體位置X1、X2、X3。

④根據式(12)、(13)更新系數向量,根據式(15)～式(17)更新其他個體的位置。

⑤依照式(18)～式(20)將更新的灰狼位置進行離散化。

⑥若沒達到最大迭代次數,則返回步驟③,否則迭代結束,并輸出全局最優解。

3 仿真及結果分析

利用MATLAB 建立仿真實驗環境。本文提出的基于簇的認知無線傳感器網絡,將本文改進二進制灰狼優化算法(IBGWO)與傳統灰狼(GWO)、粒子群(PSO)和遺傳(GA)算法進行比較,分別通過對比分析網絡最大剩余能量、次用戶的接入公平性四種算法的性能,驗證IBGWO用于解決認知無線傳感器網絡頻譜分配問題的有效性與優越性。

在本文的網絡模型中,每個簇內的傳感器節點只與簇頭通信,設次用戶共I個,主用戶數為J,設可用信道數等于主用戶數。由公式(4)可知,節點i的能耗與節點i和簇頭間的距離di有關,傳感器節點隨機分布,則距離公式為:

di=1+9×rand( ),?i∈[1,I]

(24)

隨機生成當前傳感器節點的剩余能量,如式(25)所示:

(25)

式中:100 000表示網絡的每個節點的初始能量。設信道從空閑到占用的狀態轉移概率為:

p(j)=0.1+0.09×rand( ),?j∈[1,J]

(26)

3.1 算法性能比較

設置次用戶數I=12,主用戶數J=18,一個主用戶對應一條可用信道,最大迭代次數Maxiter=200。圖3和圖4分別表示的在30種不同的傳感器節點和主用戶節點分布位置,4種算法進行頻譜分配得到的網絡總剩余能量和認知用戶數接入公平性。可得知,IBGWO算法在不同的用戶地理位置分布情況下,其網絡總的剩余能量和次用戶接入公平性皆大于其他算法。

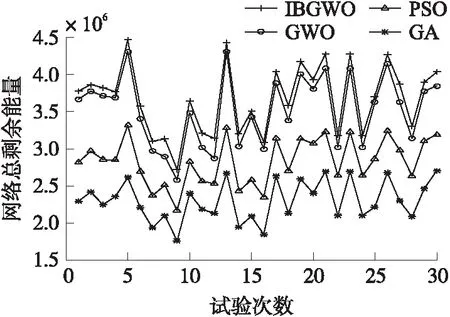
圖3 不同用戶位置情況網絡總剩余能量

圖4 不同用戶位置情況次用戶接入公平性

圖5表示四種算法在進行一次仿真時網絡總剩余能量優化過程。次用戶數I=12,主用戶數J=18。從搜索精度上看,IBGWO 算法在優化過程中尋找的頻譜分配方案,能使網絡達到更大的剩余能量。從收斂速度來看,IBGWO算法在30代左右就能收斂、GWO算法在45代左右收斂、PSO算法在55代左右收斂,GA算法在110代左右收斂,其中GA算法收斂速度較其他算法慢很多,且極易陷入局部最優。綜上,IBGWO收斂速度比其他算法快,尋優精度更高。

圖5 網絡總剩余能量優化過程

3.2 可用頻譜數量對頻譜分配的影響

在認知無線傳感器網絡中,傳感器個數、發射功率、主用戶的授權頻譜使用情況、地理位置等都可能在不斷變化,進而影響網絡總剩余能量。圖6和圖7 分別表示在次用戶數I=15,主用戶數J的取值從10逐漸增加到30時,網絡平均剩余能量以及對次用戶接入公平性與可用頻譜數之間的關系。當可用頻譜數增加時,次用戶接入授權信道的選擇變多,用戶間的沖突就會變少,則網絡平均剩余能量和次用戶接入公平性增加。由圖6、圖7可知,IBGWO算法的頻譜分配方案,其獲得的平均剩余能量和次用戶接入公平性都高于其他算法。

圖6 可用頻譜數對平均剩余能量的影響

圖7 可用頻譜數對次用戶接入公平性的影響

3.3 次用戶數量對頻譜分配的影響

為了進一步對比四種算法的性能,分析當監測區域中的次戶數量發生改變時,對相關算法將會產生怎樣的影響。圖8和圖9分別表示在主用戶數J=15,次用戶數I的取值從10逐漸增加到30時,網絡平均剩余能量以及對次用戶接入公平性與次數之間的關系。由圖8、圖9可知,當網絡中主用戶數即可用信道數固定時,隨著次用戶數增加,用戶之間干擾沖突增加,網絡負荷也隨之加重,導致網絡平均剩余能量和次用戶接入公平性不斷減少。但是IBGWO的網絡平均剩余能量和次用戶接入公平性始終優于GWO、PSO和GA算法。

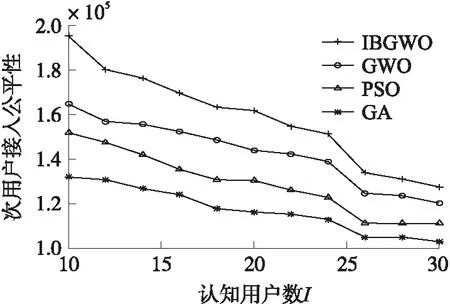
圖9 次用戶數對次用戶接入公平性的影響

4 結束語

針對WSN的使用的ISM頻段資源稀缺及電量消耗問題,本文將WSN和認知無線電的頻譜分配技術結合,建立了基于主用戶行為的能量消耗模型,提出基于改進二進制灰狼優化算法的頻譜分配方案。仿真結果表明,改進的算法以最大化網絡總剩余能量為目標,在保證主用戶正常傳輸的情況下,具有較好的分配效果、延長網絡生存周期。與其他三種算法相比,

IBGWO算法能獲得更高的網絡總剩余能量和次用戶接入公平性,更適用于無線傳感器網絡。