雷電快電場測量儀幅頻特性的時域標定方法研究*

賈 晟,石立華*,邱 實,孫 征,李 云,周穎慧

(陸軍工程大學電磁環境效應與光電工程國家重點實驗室,南京 210007)

自上世紀70年代以來快電場測量儀開始被應用于自然閃電和人工引雷情況下地面垂直電場的測量[1-3]。快電場測量儀可以捕捉雷電過程中的瞬態變化,記錄電場波形變化細節[4],使得其在閃電起始過程定位[5]、通道特性研究[6]等方面發揮重要作用,成為雷電觀測的基本手段之一。

IEEE標準指出,校準電磁脈沖傳感器時域參數時,應該考慮其頻域的特性。標準中給出了兩種校準方法,標準天線法和標準場法[7]。其中,標準場法的校準原理是:為待校準的傳感器提供可準確計算的參考電場,將傳感器置于電場環境中校準測量。該標準中指出產生標準電場的設備包括TEM室、GTEM室、波導等設備。TEM室(Transverse Electromagnetic cell)結構簡單,檢測方法簡便,可以產生均勻性良好的電場,作為標準電場[8-9]。其內部電場幅值可通過輸入電壓與結構尺寸參數計算出,其金屬外殼可以屏蔽外界電磁環境干擾和避免內部電場對外界輻射,提高了實驗結果的可靠性[10]。

幅頻特性曲線常用的標定方法為頻域標定法,原理是將連續正弦波作為激勵饋入到TEM小室,測量每個頻點處傳感器的響應與饋入的連續波幅值,繪制傳感器的幅頻特性曲線[11]。除此以外,還可以通過時域方法標定傳感器的幅頻特性曲線。由傳感器輸入、輸出時域波形建立傳感器的數學模型,描述系統的傳遞函數,最終得到該傳感器的幅頻特性曲線。這種時域標定方法屬于系統辨識理論的范疇,當前一些學者運用該方法來研究傳感器的特征參數。石立華等[12]人研究了脈沖磁場傳感器的時域標定問題,基于系統辨識理論建立了傳感器的時域模型和誤差修正模型。孟萃等[13]人建立了時域動態模型來研究核電磁脈沖傳感器的靈敏度系數一致性問題。譚堅文等[14]人采用時域方法針對脈沖電流探頭的輸出波形低頻失真建模及校正。

快電場測量儀用于捕捉雷電過程中的細節事件。由于設計傳感器時靈敏度與時間常數不能兼顧[4],因此傳感器輸出信號中存在低頻失真的現象。若想通過傳感器所記錄的波形還原電場變化,那么補償低頻失真是關鍵內容。因此,使用前需要明確傳感器的幅頻特性[15-17],在波形失真的情況下根據時域波形對實測數據實現動態校正補償,是傳感器響應信號后處理的重要環節。

本文基于輸入-輸出誤差模型理論,依據標準場法的校準原理,搭建了快電場測量儀幅頻特性曲線標定系統,采用最終預報誤差法辨識模型階數,建立傳感器系統的最優模型,對快電場測量儀(以下簡稱“快天線”)幅頻特性展開時域標定,并與頻域標定結果和時域FFT標定結果作對比。通過設計快天線的逆系統,對輸出信號補償低頻失真,還原真實電場變化。實驗結果表明,基于輸入-輸出誤差模型的時域標定法能夠準確標定快電場測量儀的幅頻特性曲線,所設計的逆系統可以很好的還原電場信號。

1 傳感器幅頻特性標定方法

傳感器幅頻特性標定方法可分為時域和頻域標定。頻域標定是采用不同單頻點的連續波來標定傳感器的幅頻特性特性曲線,而時域標定本質上是建立數學模型來求解傳感器的傳遞函數。

1.1 幅頻特性頻域標定方法

將不同單頻點連續正弦波饋入TEM小室,記TEM小室輸出電壓為V1,快天線響應電壓為V2,記錄實驗中每次TEM小室輸出電壓V11、V12、V13、V14、V15……和對應的快天線響應電壓V21、V22、V23、V24、V25……,則幅頻響應H(f)可以表示為:

(1)

根據式即可繪制出傳感器的幅頻特性曲線。

1.2 幅頻特性時域標定方法

1.2.1 輸入-輸出誤差模型理論

系統辨識理論作為一種“黑箱”建模理論,在電磁脈沖傳感器時域測量與波形校準等方面發揮了重要作用。

輸入-輸出誤差模型是系統辨識理論中的一種線性時不變模型。它是采用數學的方法對系統的輸入、輸出數據提煉出數學模型,該模型以緊湊形式描述系統的傳遞函數,表達出系統的動態特性[18]。

快天線電場傳感器可視為線性移不變(LSI)系統,設輸入信號為u(k),輸出信號為z(k),則有:

(2)

式中:B(z-1)=b0+b1z-1+b2z-2+b3z-3+…+bmz-m,A(z-1)=1+a1z-1+a2z-2+a3z-3+…+anz-n,ε(k)是誤差項。因此對于傳感器系統,其傳遞函數H(z)可用多項式B(z-1)和A(z-1)表示,

(3)

從z域變換到頻域,根據z=ejω和ω=2πfi/fs,所以,

(4)

因此,可以通過數學模型的傳遞函數獲得傳感器系統的幅頻響應等信息。

1.2.2 模型階次辨識

為使所建立的數學模型與實際系統高度吻合,式中B和A的階數nb和na是重要的影響因素。本文采用最終預報誤差法FPE(Final Prediction Error)來辨識模型階數nb和na,建立最優數學模型。最終預報誤差法是選用預報誤差項作為準則函數,當預報誤差項最小時,其對應的階數就最接近真實模型的階數,此時的數學模型將與實際系統一致性很好。

考慮到實驗系統本身存在的白噪聲,將式改寫成最小二乘格式,

z(k)=hT(k)θ+ε(k)

(5)

式中

(6)

因此,預報誤差可表示為

(7)

(8)

1.2.3 時域分步標定

方波具有豐富的頻域分量,其上升沿含有高頻分量,可以反映出傳感器的高頻響應特性,其“平頂”降落可以反映出傳感器的低頻響應特性。受普通示波器采樣深度的限制,要想獲得系統準確的高頻和低頻信息,需要采集不同時間尺度的輸入和輸出波形。因此,在時域標定過程中選擇不同脈寬的方波作為輸入波形,分步標定快天線的高頻和低頻響應。

1.3 幅頻特性時域FFT標定方法

設傳感器輸入信號為x1,輸出響應為y1,對傳感器的輸入與輸出時域波形分別做傅里葉變換,對應的頻域為|Fx|、|Fy|,則頻域響應H(f)為

(9)

由式可得傳感器的幅頻特性曲線。

圖1 實驗設置圖

2 幅頻特性標定實驗

2.1 實驗系統設置

本文基于TEM小室搭建了標準場校準系統[19],實驗設置如圖1所示。實驗中采用Rigol DG4162型函數/任意波形發生器(以下簡稱“信號發生器”)作為信號源,內阻為50 Ω,其特點是輸出波形穩定,幅值準確,波形失真程度低,用于輸出穩定連續的正弦波和方波。采用Tek 3024型示波器采集數據,該示波器帶寬范圍可達200 MHz,采樣率為2.5 GHz,最小水平分辨率為2 ns/格,最大垂直分辨率為 10 mV/格,完全滿足實驗要求。實驗時,設置示波器通道內阻均為50 Ω。

將快天線連接電源,置于TEM小室的下層空間中央位置,保持天線的圓形平板與TEM小室的中間隔層平行,避免由于人為因素引入實驗誤差。信號發生器輸出端口通過同軸線向TEM小室饋入激勵信號。TEM小室另外一端通過同軸線連接至示波器通道一,監測饋入TEM小室的波形;快天線的輸出端口連接至示波器通道二,監測快天線響應。

2.2 頻域標定

將不同頻點的正弦波饋入TEM小室,在小室下層空間產生均勻電場作為傳感器輸入,快天線的響應幅值隨頻率變化而動態變化。實驗時利用信號發生器產生幅值為20 V、不同頻率的正弦波,注入TEM小室,按照每十倍頻程記錄一組TEM小室輸出電壓V1和快天線響應電壓V2(根據具體情況可以適當增加頻點數)。根據式,連續正弦波標定快天線幅頻特性曲線的結果如圖2所示。從圖2中可以看出由于讀數誤差的存在,幅頻曲線高頻部分光滑程度較差,快天線-3 dB帶寬范圍約為200 Hz～6 MHz。

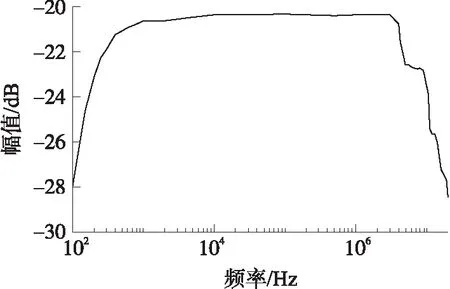
圖2 連續波標定幅頻曲線結果

2.3 基于輸入-輸出誤差模型的時域標定

2.3.1 傳感器高頻響應標定

設置示波器采樣率為2.5 GHz,采樣長度為10k個點,示波器水平分辨率為40 ns/格。為了更好獲取快天線高頻響應,向TEM小室注入頻率為1 MHz的方波,采集輸入與輸出波形,建立數學模型。選取目標數據段,即輸入波形和輸出波形的上升沿,如圖3(a)所示。

根據FPE定階法,選取最終預報誤差最小情況下的模型階數作為最優模型階數。確定多項式B和A的階數分別為6、6,傳遞函數H(z)為

H(z)=(5.358×10-4+0.003 8z-1-9.755×10-4z-2-
0.007 5z-3+2.696×10-4z-4+0.003 9z-5)×

(1-0.079z-1-2.851z-2+0.131 5z-3+2.73z-4-
0.056 7z-5-0.876z-6)-1

(10)

比較模型輸出結果和傳感器輸出結果,波形吻合程度高達96%,如圖3(b)。將H(z)由z域變換到頻域,因此可求出快天線傳感器高頻部分幅頻響應,如圖3(e)。快天線高頻的-3 dB帶寬范圍(即>-23 dB范圍內)是<7 MHz。

2.3.2 傳感器低頻響應標定

設置示波器采樣率為1 MHz,采樣長度不變,水平分辨率為200 μs/格。向TEM小室注入方波信號,頻率為400 Hz,獲得快天線傳感器的低頻部分響應,如圖3(c)。選取波形時確保“平頂”部分完整。根據FPE定階法,分別確定多項式B和A的階數為6和9,其傳遞函數H(z)為

H(z)=(0.0611+0.0993z-1+0.0226z-2-0.0569z-3-
0.0834z-4-0.0426z-5)(1+1.198z-1-0.358z-2-
1.1545z-3-0.926z-4+0.0088z-5+0.448z-6+
0.1537z-7-0.159z-8-0.2035z-9)-1

(11)

比較模型輸出結果與傳感器響應結果,模型辨識結果與傳感器輸出結果吻合程度為95.6%。根據系統傳遞函數求出快天線低頻部分的幅頻特性曲線,如圖3(f),快天線低頻的-3 dB帶寬范圍是>200 Hz。

基于輸入-輸出誤差模型時域標定幅頻曲線結果較為光滑,高頻段和低頻段連接部分幅值差小于0.2 dB,誤差在可接受范圍內。

圖3 基于輸入-輸出誤差模型的幅頻特性時域標定結果

圖4 時域FFT標定結果

2.4 時域FFT標定

仍選用基于輸入-輸出誤差模型時域標定的數據計算傳感器幅頻特性曲線,結果如圖4所示,通過比較可以看出傅里葉變換獲得的曲線效果較差,由于高低頻內噪聲的存在,圖4中曲線振蕩嚴重,突出體現在3 MHz以上和3 kHz～10 kHz之間。采樣長度不足的問題導致低頻段的幅頻曲線上點數較少,曲線光滑度較差。

圖5 模型重構結果與原始輸入對比

3 波形失真補償

對失真波形補償,本質上是設計快天線的逆系統,對失真波形重構。建立快天線的逆系統模型,將快天線響應作為模型輸入,模型的輸出就是實際上快天線的輸入。以圖5中快天線輸入和失真波形為例,通過重構逆系統、模型辨識,確定逆系統傳遞函數H(z)為

H(z)=(10.38-3.526z-1-4.17z-2+1.11z-3-5.52z-4-
8.71z-5+6.44z-6+1.91z-7-2.11z-8+4.19z-9)×

(1-0402z-1-0.354z-2+0.1996z-3-0.619z-4-
0.837z-5+0.661z-6+0.156z-7-0.272z-8+
0.5z-9-0.0325z-10)-1

(12)

根據逆系統傳遞函數得到重構后的波形如圖5所示。對比模型輸出和快天線輸入,重構結果很好,波形趨勢一致。

4 結果對比與分析

①圖6(a)為頻域標定結果和基于輸入-輸出誤差模型時域標定結果的對比。對比幅頻特性曲線頻域標定結果和時域標定結果,可以看出,兩種方法的結果的“平頂”部分吻合程度基本一致。在傳感器系統響應-3 dB帶寬范圍內,時域標定結果與頻域標定結果一致。在-3 dB帶寬范圍外,兩種方法所得結果的吻合程度也比較高。圖6(b)為時域FFT標定結果和基于輸入-輸出誤差模型時域標定結果的對比,模型辨識方法的優越性非常明顯。

②幅頻曲線標定結果可以看出,在低頻截止頻率段與高頻截止頻率段,快天線靈敏度系數可看作頻率f的函數,而在中頻段,快天線響應幅值與輸入信號頻率大小無關,可看作一常數。因此在截止頻段使用峰值標定傳感器靈敏度是沒有意義的,即在標定傳感器靈敏度之前,應首先明確傳感器的幅頻特性。

圖6 連續波頻域標定、時域標定和時域FFT標定結果對比

③頻域標定法、基于輸入-輸出誤差模型的時域標定法和時域FFT標定法比較:

基于頻域測量的幅頻曲線標定法基于時域測量的輸入-輸出誤差模型標定法基于時域測量的FFT標定法實驗設備連續波信號源加接收機,或網絡分析儀脈沖信號源加示波器脈沖信號源加示波器特點小信號測量、非參數化的幅頻曲線脈沖大信號測量、參數化模型脈沖大信號測量、非參數化模型應用獲知頻帶特性,獲得通頻帶內的幅度校準系數獲知波形響應特征、頻帶特性,獲得全波形的校準模型,可直接用于失真恢復獲知波形響應特征、頻帶特性,FFT和逆FFT在高頻段噪聲影響嚴重

④幅頻特性曲線標定過程中,確保實驗步驟連續,一次性完成數據采集,以保證傳感器和相關實驗設備所處狀態一致。

5 傳感器標定結果的實際應用

本文方法獲得的電場傳感器標定結果不僅為確定傳感器靈敏度系數和響應帶寬提供了描述參數,同時也為校正傳感器失真提供了有效方法,在雷電電磁場波形的準確測量中獲得了應用。

圖7為一次地閃回擊過程的快慢天線測量結果及快電場傳感器的校正結果。其中,慢天線通常用于測量雷電過程的電場慢變化,主要反映放電過程的電荷變化引起的電場抬升,這類天線具有較大的時間常數,低頻特性良好;而快天線主要反映電場快速變化,低頻響應不足,因此存在后沿保持能力不足,類似于圖3(d)中的“平頂下降”現象。利用實驗室階躍波標定獲得的結果,根據建立的快天線逆系統模型對實測快天線數據低頻補償,并將結果與慢天線數據對比。

圖7 模型補償結果與實測結果比較

由圖7可看出,對快天線數據做低頻補償后取得較好的效果,后沿得到有效校正,與慢天線反映的電場抬升趨勢吻合一致。

6 總結

本文基于輸入-輸出誤差模型理論對快電場測量儀建立數學模型,分步計算出快電場測量儀的幅頻特性曲線,并與頻域標定方法、時域FFT標定方法作比較。建模過程中采用最終預報誤差法(FPE)確定傳遞函數的最優階數,提高了模型吻合度。本文設計了快電場測量儀的逆系統模型對失真方波和實測雷電電場數據校正補償,均取得了較好的結果。