中心支撐鋼框架在空腹效應作用下抗連續倒塌分析

喬惠云， 魏建鵬， 田黎敏

(1. 福建工程學院 土木工程學院，福州 350118； 2. 福建省土木工程新技術與信息化重點實驗室，福州 350118；3. 西安建筑科技大學 土木工程學院，西安 710055)

連續性倒塌是指初始局部構件破壞向其它構件擴展，最終導致結構整體破壞或者大范圍區域的倒塌。框架結構倒塌過程可能經歷彎曲效應、懸鏈線效應，壓拱效應和空腹效應。常用的單層子結構模型可以反應前三種抗倒塌效應，相應的研究較多。李易等[1]基于能量方法分析了彎曲效應的工作機理。Yang等[2-5]通過靜力加載試驗研究梁柱節點在中柱失效下的力學性能，分析子結構從彎曲效應向懸鏈線效應發展情況。周育瀧等[6]建立了壓拱效應下梁板子結構的連續倒塌抗力分析模型。而空腹效應只存在于空間框架結構，Sagiroglu等[7]對某七層鋼筋混凝土進行抗倒塌研究，指出空腹效應的特性是豎向構件對各層內力重分配的結果。課題組曾采用頂層子結構模型，保守估計了空腹效應的貢獻[8-9]，但是簡化子結構模型仍然避開結構的整體受力特點，空腹效應在空間結構的工作原理還需進一步研究。

支撐框架結構是一種抗震性能良好的結構體系，具有較高的彈性剛度和強度特性，常被用于提高結構在水平地震作用下抗震性能[10-11]，能否用于構件失效后的抗連續倒塌需要進一步研究。施煒等[12]研究發現按抗震規范設計的多層框架結構，抗倒塌能力存在不足，需要采取一定的構造措施。失效柱正上方各層類似于空腹桁架，傅傳國等[13]在空腹桁架底層施加了預應力，使結構在水平和豎向荷載作用下，整體工作性能良好。缺點是失效柱位置不確定，底部加強難以實現。Macarena等[14]在已有建筑的頂層布置轉換梁，將豎向荷載轉移到屋頂，使舊建筑滿足抗連續倒塌規范要求，按此思路，本文在常用中心支撐框架的頂層布置水平支撐，研究框架結構在該構造措施下的抗倒塌性能，以及空腹效應發揮的作用。

1 多層鋼框架去柱模擬

本節首先用數值方法模擬已有多層框架去中柱試驗，李國強等[15]和謝甫哲等[16]分別對多層鋼框架進行動力分析，瞬時拆除中柱，給出結構的抗倒塌性能；隨后，分析中柱失效后剩余結構的內力分布，并指出空腹效應的特點。

1.1 李國強試驗模擬

選取試驗中一個試件，記為Frame A，立面圖與荷載布置如圖1所示，框架梁和柱的截面均采用H54×50×4×4(mm)，節點采用全焊節點，配重大小分別為P1=385 kN，P2=2.1 kN，用擺錘沖擊的方法引起中柱瞬時失效。

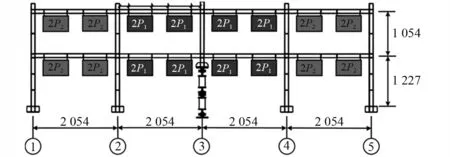
圖1 Frame A的立面圖與荷載布置Fig.1 Elevation and load distribution diagram of Frame A

采用ABAQUS中梁單元B22建立有限元模型，如圖2所示，模型考慮符合鋼材微觀機制的應力三軸度損傷準則[17]，阻尼為瑞雷阻尼。配重施加方式不是以常用的外荷載形式施加，而是將配重折算成一定體積和密度的質量塊，這是因為配重參與結構的固有頻率，影響結構的動力特性。

中柱突然失效，材料受應變率影響很大，鋼材的應變率采用Cowper-Symonds模型[18]，屈服應力與應變率的關系為

圖2 Frame A有限元模型Fig.2 Finite element model of Frame A

(1)

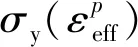
分析柱失效點位移Δ隨時間t的變化情況，如圖3所示，并將模擬值與試驗值對比，發現有限元結果與試驗結果基本一致，說明有限元模型可以反映試件的初始狀態及柱失效后的動力反應；圖中還列出忽略應變率的有限元模擬結果，與試驗結果差別很大，說明動力模擬應當考慮應變率的影響。

圖3 Frame A失效點位移時程曲線Fig.3 Displacement time history curve of Frame A at the failure point

圖4為失效跨梁端彎矩M和軸力F隨時間t的變化情況，結構振動穩定后，梁端彎矩值大小接近，約為7.1 kN·m，彎矩分布規律與破壞前的結構一致；失效跨各層梁的軸力分布差別較大，第1、第2層的軸力符號相反，穩定后的值分別為26 kN和-11 kN。頂層的軸壓力是豎向構件對各層內力重分配的結果，表現出空腹效應的特點。

圖4 Frame A 失效跨內力變化曲線Fig.4 Internal force curve of Frame A in failure span

1.2 謝甫哲試驗模擬

圖5為謝甫哲等研究中的三層四跨平面鋼框架，第1層的層高為510 mm，第2、第3層的層高為400 mm，跨度為500 mm。梁和柱均采用方形鋼管，梁截面為□20×1.2(mm)，柱截面為□30×1.2(mm)。

試驗包括兩組試件，截面形式與幾何尺寸都相同，只有配重不同，第一組處于彈性狀態，中柱瞬時失效后，結構經過短時間的振蕩，重新達到穩定，配重G1=G2=G3=452.8 N，將試件標記為Frame B；第二組試件發生彈塑性破壞，并最終倒塌，配重G1=G2=2 563.7 N，G3=2 753.8 N，標記為Frame C。

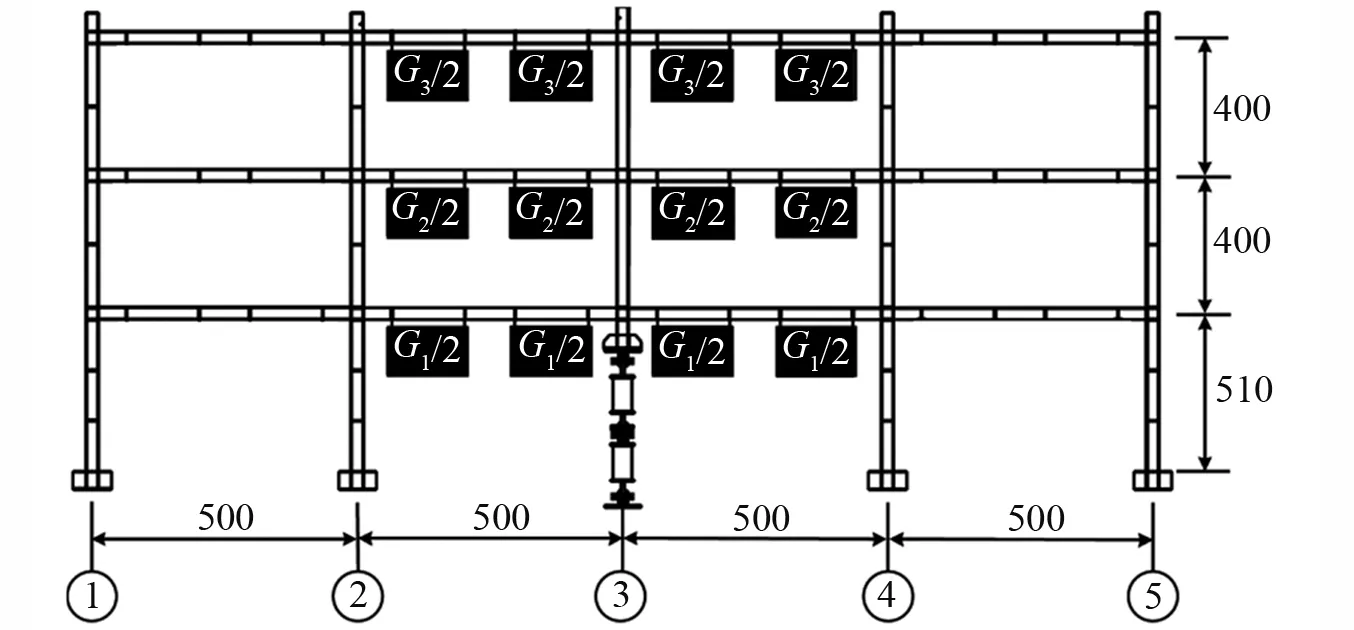
圖5 Frame B和Frame C的立面圖與荷載布置Fig.5 Elevation and load distribution of Frame B and C

采用梁單元B22建立有限元模型，用隱式動力法進行分析。材料的彈塑性本構模型考慮損傷與應變率，并計入瑞雷阻尼的影響。試件Frame B處于彈性變形階段，主要依靠梁端彎矩抵抗不平衡荷載，分析試件在中柱失效后的受力特點，特別是各層梁的軸力分布情況，圖6給出部分計算結果。

圖6(a)為Frame B在失效點的位移時程曲線，將有限元模擬結果與試驗結果對比，振幅和頻率基本吻合，符合試驗的動力特性。圖6(b)為失效跨軸力時程曲線，振動穩定后，第1層為拉力192 N，沒有發展懸鏈線效應；第3層為壓力-340 N，有空腹效應的特點；第2層為拉力99 N，大小在其余兩層之間。第1、第2、第3層軸力合力等于-49 N，遠小于各層軸力，認為在小變形下各層軸力平衡。

圖6 Frame B部分計算結果Fig.6 Part of the calculation results of Frame B

試件Frame C進入塑性變形階段，結構發生大變形，懸鏈線效應發揮作用，分析試件在中柱失效后的受力特點，圖7給出部分計算結果。

圖7(a)為Frame C在中柱失效位置的位移時程曲線，并將其與試驗結果對比，動力反應(振幅和頻率)與試驗結果相差不大，認為有限元模型符合試驗的力學特性。圖7(b)為Frame C在失效跨的軸力時程曲線，第1層的拉力值(6 700 N)遠大于第2、第3層的壓力值(-683 N，-890 N)，各層軸力合力為5 127 N，數值大小與第一層軸力接近。第1層向懸鏈線效應發展，而第2、第3層表現出空腹效應的特點，該現象也可以由圖8的軸力云圖反映。

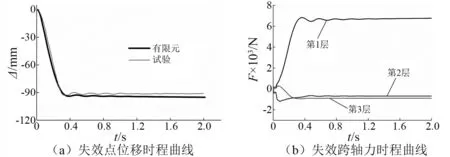
圖7 Frame C部分計算結果Fig.7 Part of the calculation results of Frame C

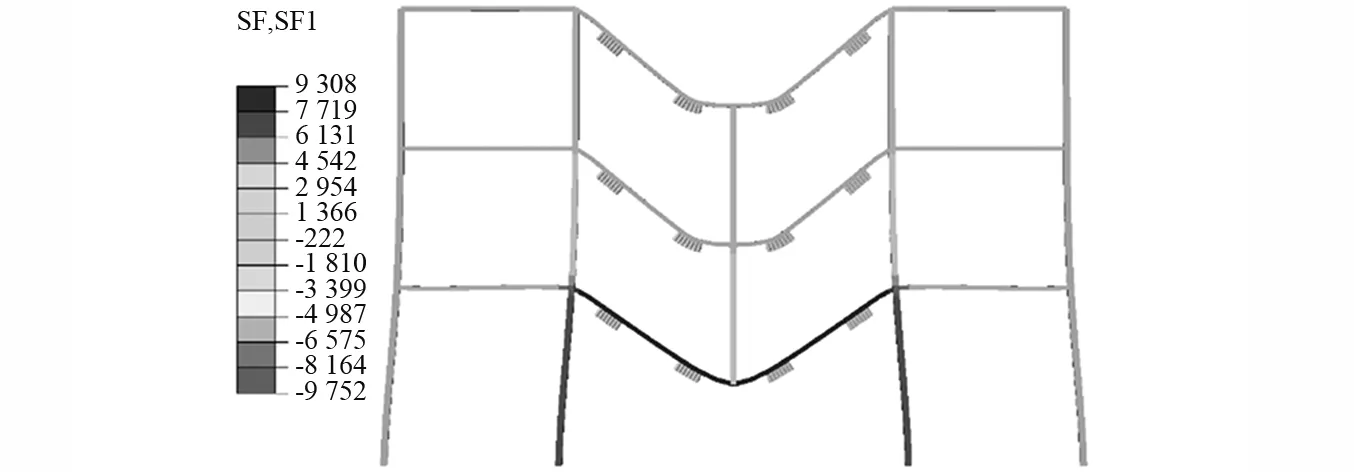
圖8 Frame C軸力云圖Fig.8 Axial force cloud of Frame C

2 空腹效應

2.1 空腹效應工作原理

中柱失效后，剩余結構作為一個整體共同變形，變形主要集中在失效跨，而相鄰跨的變形較小，分析空腹效應的工作原理，取失效跨為研究對象，將相鄰跨作為失效跨的邊界。

結合多層框架Frame A，Frame B，Frame C的軸力分析結果，無論結構為小變形(彈性狀態)還是大變形(彈塑性狀態)，頂層梁的軸力為壓力；底層梁的軸力為拉力，底層在大變形時表現出懸鏈線效應；中間層梁軸力相對較小，方向可能為拉力，也可能為壓力。框架各層梁的軸力形成新的力偶矩，產生空腹效應，與梁端彎矩一起抵抗連續倒塌。

通過對多層框架Frame A，Frame B，Frame C模擬分析還發現，大變形時，底層梁的軸力遠大于其它層，認為軸力合力主要作用在底層梁；小變形時，各層軸力平衡，仍然可以認為軸力合力主要作用在底層梁，基于此考慮，計算抗力PB將分為小變形和大變形兩種情況，并將各層的內力移動到底層。

以n層框架為例，如圖9(a)所示。假設梁柱節點剛度足夠大，能夠傳遞梁和柱中的塑性彎矩。失效柱兩側的跨度分別為L和L′；n為總層數；Hi為第i(i=1,2，…，n)層的層高；Mi，Fi和Vi分別為第i層左側的梁端彎矩、軸力和剪力；M′i，F′i和V′i分別為第i層右側的梁端彎矩、軸力和剪力。

將左側各層梁的軸力向第1層梁端(點O)移動，將右側各層梁的軸力向點O′移動，分別得到兩側軸力的合力Fo和F′o，一般情況下，Fo=F′o。與此同時，各層軸力形成的力偶矩Mo和M′o，可以表示為

(2)

(3)

采用同樣的方法，將各層梁端的剪力和彎矩向第1層移動，得到剪力和彎矩的合力，分別表示為

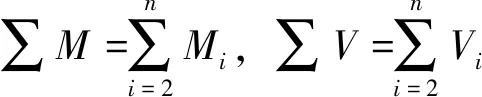
(4)

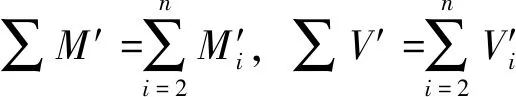
(5)

經過對各層軸力、剪力和彎矩求合力計算，多層框架結構可以簡化為圖9(b)計算示意圖。

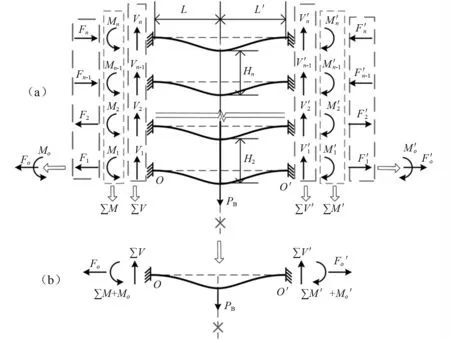
圖9 中柱失效后空腹效應示意圖Fig.9 Schematic diagram of vierendeel action after middle-column failed

小變形時，各層軸力的合力Fo與F′o接近于0，由彎矩抵抗連續倒塌，抗力PB包含兩部分：①由梁端彎矩∑M和∑M′貢獻，這部分記為PB1；②由空腹效應產生的力偶Mo和M′o貢獻，這部分記為PB2。在圖9(b)中，若僅有PB1作用在梁上，由力的平衡條件，抗力PB1與梁端彎矩∑M和∑M′的關系表示為

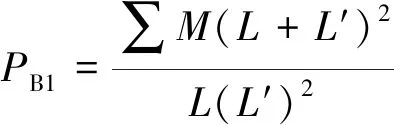
(6)

若僅有PB2作用在梁上，由力的平衡條件，抗力PB2與力偶Mo和M′o的關系表示為

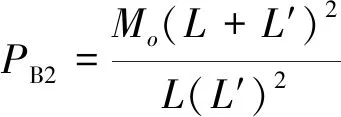
(7)

大變形時，軸力合力Fo和F′o與底層梁軸力接近，有Fo=F′o≈F1，部分梁發展了懸鏈線效應，結構除了由彎矩抵抗連續倒塌，還由梁的軸拉力提供部分抗力，將其記為PB3。 假設w為中柱失效點處的位移，由力的平衡條件，抗力PB3與軸力Fo的關系為

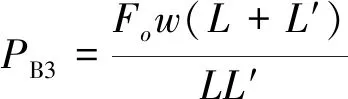
(8)

綜合考慮梁端彎矩，以及軸力作用下的懸鏈線效應和空腹效應，多層框架的抗力需求PB由式(6)、式(7)和式(8)求和得到

(9)

2.2 算例驗證

選取“4”節實例的中間幾跨，驗證“2.1”節抗力計算的合理性，梁截面為H500×200×10×18(mm)，柱截面為H350×300×20×30(mm)，層高H=4.2 m，左邊兩跨L=7.72 m，右邊兩跨L′=6.5 m。采用ABAQUS中的梁單元B22建模，在柱失效點處通過位移加載方式完成Pushdown分析。失效點處達到最大位移時，剩余結構的軸力分布與變形如圖10所示。

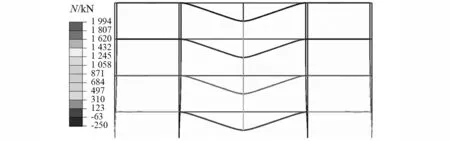
圖10 剩余結構的軸力分布與變形Fig.10 Deformation and axial force distribution for remainder structure

分析失效跨梁端彎矩、軸力隨柱失效點處撓度w的變化情況，圖11給出左側梁端內力變化曲線。大變形時，第1層梁的軸拉力發展到懸鏈線效應，并導致第1層彎矩減小；第2～第4層軸力較小，梁端彎矩接近，其中第4層軸力為壓力，剩余結構主要由彎曲效應抗倒塌，并發生空腹效應。

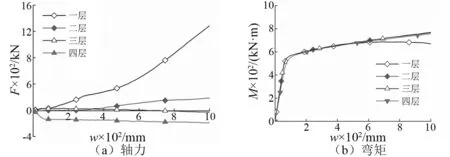
圖11 左梁端內力變化曲線Fig.11 Internal force curve of left beam-end

按照“2.1”節建議方法計算剩余結構的抗力PB，包含梁端彎矩貢獻PB1，空腹效應貢獻PB2和懸鏈線效應貢獻PB3，并和有限元模擬結果對比，如圖12所示，有限元結果與理論計算結果吻合良好。圖12還列出了只考慮彎曲效應的結果(PB1)和忽略空腹效應的結果(PB1+PB3)，對比PB1曲線和PB1+PB3曲線發現，懸鏈線只在大變形時發揮作用；對比PB曲線和PB1+PB3曲線發現，本例中空腹效應的貢獻為12%，多層框架的空腹效應不應該被忽略。

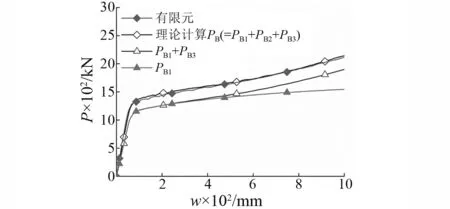
圖12 剩余結構的抗力變化曲線Fig.12 Resistance curve for remainder structure

3 中心支撐框架抗連續倒塌

V形(倒V形)支撐是中心支撐框架最常用的支撐形式，能夠提供更多的空間，方便門窗洞口設置和設備放置，本節在“2.2”節算例的基礎上布置倒V形中心支撐，支撐截面采用H250×250×9×14(mm)。布置兩種類型中心支撐框架，采用Pushdown法分析中柱失效后的抗倒塌性能，并與純框架結構對比，如圖13所示。

圖13 兩種中心支撐框架Fig.13 Two steel concentrically braced frame

中心支撐框架Ⅰ為抗震設計常用的支撐體系，將中柱失效后的抗力與純框架對比，如圖13(d)中C1曲線與C0曲線，當位移w<300 mm時，小變形下梁中軸力基本不發展，C0與C1曲線重合；大變形時梁中拉力參與抵抗外荷載，柱間支撐增加了梁端約束，有利于懸鏈線效應發揮作用，C1曲線抗力值稍大于C0曲線，當w=900 mm時，前者是后者的1.3倍。

中心支撐框架Ⅱ在常用中心支撐框架Ⅰ的基礎上，布置頂層水平支撐，增強上層梁的軸向剛度，有利于空腹效應發揮作用；同時，支撐體系形成新的荷載傳遞路徑，部分重力荷載由水平支撐傳遞到相鄰結構，再由豎向支撐傳遞到基礎。最終，中心支撐框架Ⅱ的抗力如圖13(d)中C2曲線，數值遠大于C0和C1曲線。由水平支撐連接的第3、第4層梁組成整體，抗彎剛度大，向下變形前，要先克服相鄰結構的軸向約束，抗力曲線呈現先提高后降低的趨勢，峰值時刻抗力值4 300 kN，為同時刻曲線C0和C1抗力值的3倍。隨著懸鏈線效應的發展，曲線C2與其余兩條曲線的差距減小，但采用水平支撐加強的框架仍有明顯的優勢，當w=900 mm時，支撐框架Ⅱ的抗力值是支撐框架Ⅰ的1.46倍。

由以上分析發現，中心支撐框架Ⅱ比框架Ⅰ整體性加強，其水平支撐大幅提高結構的抗倒塌能力，使結構兼具抗震和抗連續倒塌性能。彎曲效應PB1、空腹效應PB2和懸鏈線效應PB3在抗連續倒塌不同階段所占比例不同，圖14列出部分結果。

小變形時，由水平支撐連接的第3、第4層梁形成的空腹效應PB2，與彎曲效應PB1共同抵抗不平衡荷載，圖14列出w=0.1 m時兩者所占比例；在懸鏈線過渡階段，梁中軸拉力參與抵抗倒塌，比如w=0.5 m時，PB3占比5%；隨變形增大，懸鏈線效應貢獻增大，空腹效應的影響相對減小，當w=0.9 m時，結構進入懸鏈線效應，PB3占比增大到25%。

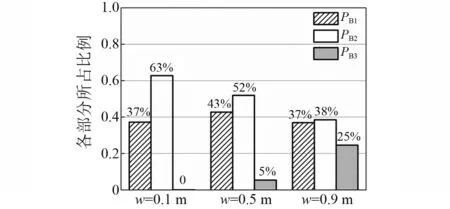
圖14 中心支撐框架Ⅱ的抗倒塌效應Fig.14 Anti-collapse mechanism of steel concentrically braced frame Ⅱ

4 實例分析

俄亥俄州立大學某綜合大樓采用鋼框架結構，由地上四層與地下一層組成，在大樓達到使用期限被拆除前，Song等先拆除底層4根柱，拆柱順序標在底層平面圖，如圖15所示。四根柱依次被拆除并分別達到穩定時，柱失效點的位移分別為6.05 cm，6.12 cm，17.93 cm和9.98 cm。

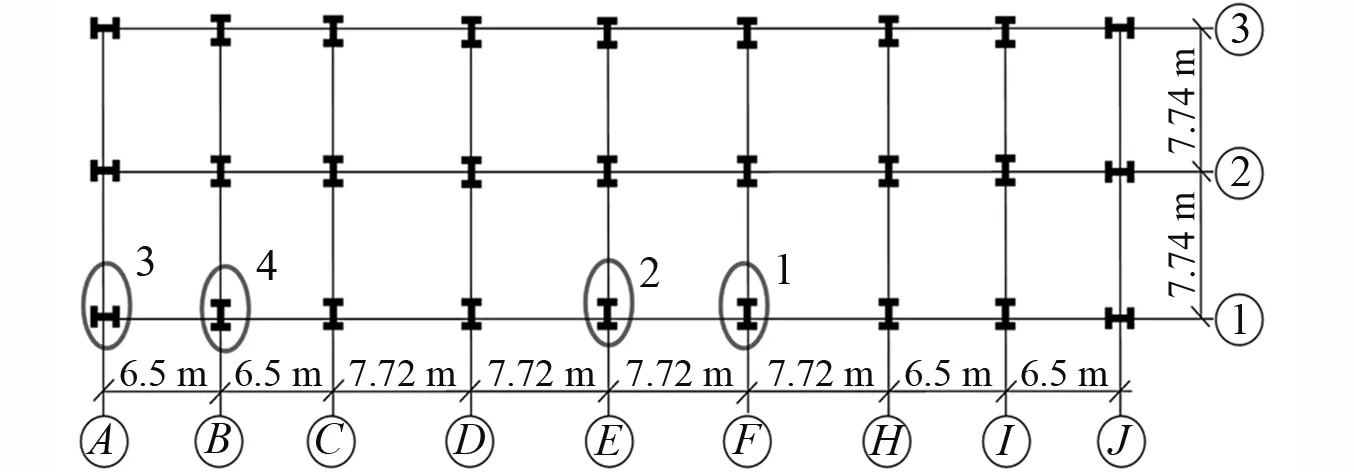
圖15 俄亥俄州立大學綜合大樓底層平面圖Fig.15 The ground plan of the Ohio Union building

模擬四根柱的拆除過程，采用有限元軟件ABAQUS的梁單元B32建模，并考慮材料與幾何非線性的影響，具體建模過程見喬惠云等的研究。每根柱的拆除分為兩步：①在0.01 s內完成柱拆除，拆除方式采用在Edit Keyword模塊加入語句*MODEL CHANGE, TYPE= ELEMENT, REMOVE； ②剩余結構在0.5 s內沒有動態激勵，動力響應在阻尼作用下趨于穩定。

將本文模擬結果與文獻[20]的結果對比，如圖16所示，各柱穩定后的失效點位移分別為6.33 cm，6.47 cm，17.75 cm，9.23 cm，與文獻[20]誤差在7.5%以內，說明本節模擬結果有效。需要說明的是，文獻[20]的位移時程曲線從4根柱都失效后開始計時，為方便與文獻結果對比，本文也采用相同時間。

圖16 本文模型與文獻[20]的柱頂節點位移對比Fig.16 Comparison of displacement above each removed column between this model and references [20]

為研究支撐體系對空間框架的抗連續倒塌作用，以俄亥俄綜合大樓為原型結構，記為Model 0，在失效柱附近布置倒V形支撐體系，建立兩個中心支撐框架模型Model Ⅰ和Model Ⅱ，支撐截面采用H250×250×9×14(mm)。Model Ⅰ在第1～4層布置豎向支撐，支撐位于圖15中CD跨和HI跨；Model Ⅱ在Model Ⅰ豎向支撐的基礎上，布置頂層水平支撐。

采用Model 0拆柱方式，瞬時拆除中心支撐框架Model Ⅰ和Model Ⅱ的兩根中柱，柱失效點的位移時程曲線如圖17所示。柱1失效后，Model Ⅰ在失效點的

穩定位移為5.58 cm，與原型框架Model 0結果(6.33 cm)接近，說明抗震常用的豎向支撐體系對抗連續倒塌貢獻有限；Model Ⅱ經過短時振蕩達到穩定平衡，穩定時位移為1.26 cm，約為原型框架結果的1/5，加入水平支撐提高結構的整體性，抗連續倒塌性能隨之提高。柱2失效后，柱失效點位移仍有相同的規律，Model Ⅱ最快達到穩定平衡，穩定時位移為1.22 cm，約為原型框架結果(6.47 cm)的1/5.3；同樣，采用豎向支撐的Model Ⅰ與原框架Model 0計算結果相差不大。

圖17 失效點的位移時程曲線Fig.17 Displacement time history curve at the failure point

兩根中柱失效后，對比Model Ⅰ與Model Ⅱ與原型框架Model 0的應力分布，圖18為柱2頂部位移達到第一個位移峰值時刻的應力云圖。Model Ⅰ與Model 0的應力分布接近，最大應力發生在失效跨，失效柱正上方的梁和剩余柱組成類似空腹桁架的結構，而提高頂層的剛度是空腹桁架的加強方式之一，所以在Model 0和Model Ⅰ頂層布置水平支撐，形成Model Ⅱ，有利于將失效跨的大部分重力由水平支撐傳到相鄰結構。

圖18 兩根中柱失效后應力云圖Fig.18 Stress cloud after column 1 & 2 removal

對比彎曲效應PB1、空腹效應PB2和懸鏈線效應PB3分別在框架Model 0，ModelⅠ，ModelⅡ所占比例，圖19為柱2頂部位移達到第一個位移峰值時刻的結果。Model Ⅰ的支撐體系增強豎向構件的剛度，有利于豎向構件對各層內力重分配，與Model 0相比，空腹效應PB2所占比例從34%提高到41%；Model Ⅱ頂層剛度較大，失效跨的重力由殘留柱傳遞到水平支撐和梁的組合結構，再由豎向支撐傳遞到基礎，形成新的傳力路徑，軸力組成的力偶矩Mo對抵抗連續倒塌起主導作用。需要說明的是，懸鏈線效應PB3在框架Model 0，ModelⅠ，ModelⅡ所占比例均較小，這是由于原結構在拆除柱前，清空了家具、工作設備等活荷載，結構只承受自身重力，遠沒有達到進入懸鏈線效應的荷載。

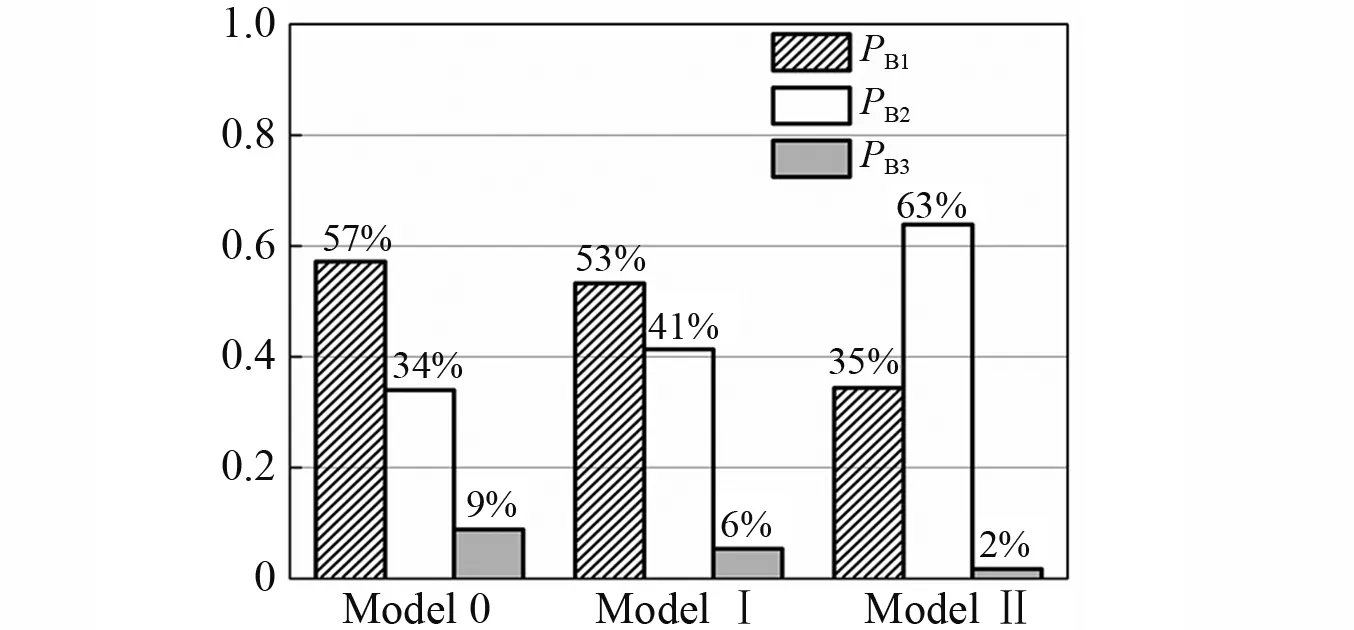
圖19 柱1失效后的抗倒塌效應Fig.19 Anti-collapse mechanism after column 1 loss

5 結 論

本文通過對已有多層框架去柱試驗的模擬，分析空腹效應的工作原理，然后對抗震常用的中心支撐框架布置水平支撐，提高空腹效應的貢獻，增強結構抗連續倒塌性能，主要結論如下：

(1) 瞬間去柱等動力模擬，應變率對材料塑性的影響較大，忽略應變率會導致位移結果偏大；同時，配重等豎向荷載通過慣性力間接影響結構的動力特性，模擬過程中，要將荷載折算成結構的密度計算。

(2) 多層框架各層梁的軸力方向不同，軸力組成一個新的力偶矩Mo，即空腹效應，與梁端彎矩以及懸鏈線效應共同抵抗不平衡荷載。

(3) 改進抗震設計常用的中心支撐框架，在結構頂層布置水平支撐，水平支撐體系可以明顯減小失效節點處位移，通過發揮空腹效應的貢獻，提高結構的抗連續倒塌性能。

(4) 將支撐體系用于俄亥俄州立大學綜合大樓，相鄰兩根中柱失效后，失效柱正上方的梁和柱組成類似空腹桁架的結構，頂層水平支撐體系使結構整體性增強，將失效跨的大部分重力傳遞到相鄰結構。