空間第二型曲線積分的計算方法

王紅喜，楊 青

(1.陜西職業技術學院 基礎課部，西安 710100；2.西安航空學院 理學院，西安 710077)

0 引言

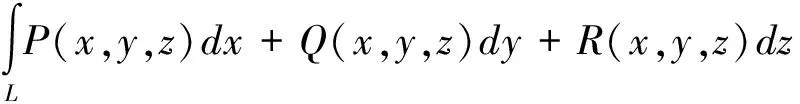
1 常用的計算方法

對于空間曲線積分的計算可分為直接計算法和間接計算法，其中直接計算是指根據曲線L的方程將其化成定積分來計算。間接計算法是指根據曲線積分與路徑無關和斯托克斯公式來計算。因此可將空間第二型曲線積分的計算分為以下情形。

1.1 直接計算

這種方法可概括為“選參代入”。

第一步(選參)：常見的空間曲線L的方程類型有參數方程和一般方程[2]。當空間曲線的方程是一般方程時，往往要將一般方程轉化成參數方程，這樣就選擇了參數。

第二步(代入)：把L的方程代入曲線積分中，積分的路徑變成了區間，也就是將曲線積分化成定積分。注意這里定積分的下限是曲線L起點處的參數值，上限是曲線終點處的參數值。

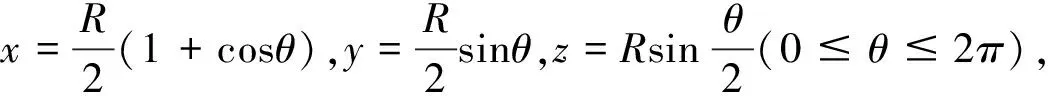
一般地，這種方法適用于第二型曲線積分的積分路徑規則，易于“選參”，并且代入后定積分容易計算。否則，我們可以考慮使用下面的計算方法。

1.2 應用空間曲線積分與路徑無關定理

用直接法計算，將曲線的一般方程寫成參數方程時，不是一件容易的事情，即使能寫出參數方程，如果被積函數形式復雜，這時將其化成定積分時也難以計算。若空間曲線積分與路徑無關，就可以選擇恰當的路徑來計算積分。

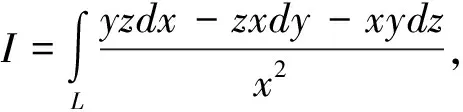
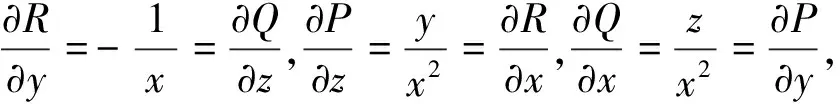
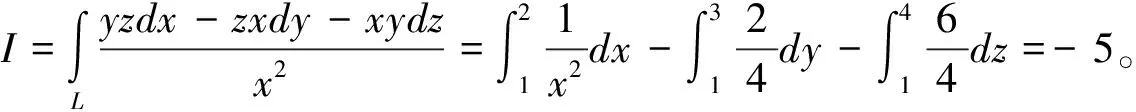
1.3 應用斯托克斯公式

斯托克斯公式將空間閉曲線積分和閉曲線張成的曲面上的曲面積分聯系在一起[3]，因此可以應用斯托克斯公式來簡化某些第二型曲線積分的計算。

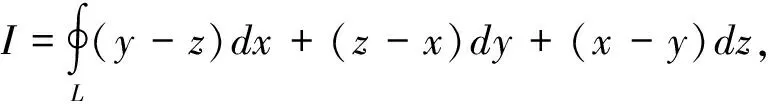
從x軸正向向負向看去取順時針方向。

(cosα，cosβ，cosγ)是指與∑同方向的單位法向量。

根據L的方向，∑取平面y-xtanα=0，方向指向∑的后側，故

應用斯托克斯公式計算第二型曲線積分時，通常是將曲線積分化成第一型曲面積分來計算，這時一定要注意閉曲線和它所張成的曲面的方向需符合右手規則。

雖然斯托克斯公式可以將空間曲線積分化成第一型曲面積分來計算，但是如果第一型曲面積分的被積函數比較復雜，那么采取這種方法達不到計算的目的。

2 常見的解題技巧

在計算空間第二型曲線積分時，適當的應用曲線積分的性質會使計算變得簡便。

2.1 利用曲線積分的牛頓-萊布尼茨公式

由空間曲線積分與路徑無關的四個等價命題知[4]，如果存在一個三元函數u(x,y,z)，使得在Ω內每一點都有du=Pdx+Qdy+Rdz，這時空間第二型曲線積分就可以用終點和起點的函數值的差來計算。只要能求出原函數，就能利用曲線積分的牛頓—萊布尼茨公式計算曲線積分。

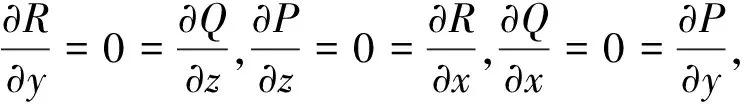
2.2 利用性質化成平面曲線積分

根據第二型曲線積分的性質[5]，如果空間第二型曲線積分的積分曲線的方程中出現z=c(y=c或z=c)(這里c是常數)，這時可將z=c(y=c或z=c)先代入空間曲線積分中去，化成平面第二型曲線積分來計算。當然，在適當的條件下，可以用格林公式計算平面第二型曲線積分。

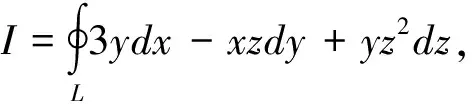
2.3 利用關于坐標面的對稱性

命題1 設被積函數是連續函數，L=L1∪L2，L1，L2關于xoy坐標面對稱，以xoy坐標面區分，L1，L2的走向相反。則

3 結語

圖1 積分曲線示意圖

本文主要歸納總結了空間第二型曲線積分的計算方法。首先從直接計算(選參代入)方法入手，然后采用曲線積分與路徑無關的條件以及斯托克斯公式來求解空間第二型曲線積分，這樣大大增強了計算空間第二型曲線積分的靈活性。最后又歸納總結了空間第二型曲線積分的一些解題技巧。