基于模糊人工勢場法的機械臂避障達點研究

韓 峰，趙 京

（北京工業大學 機械工程與應用電子技術學院，北京 100124）

0 引言

機器人的路徑規劃算法有RRT，A*等，還有一些人工智能算法。但是人工勢場法以其簡單的特點獲得了廣泛的應用。人工勢場法是由KHABIT[1]提出的。王俊龍等[2]利用虛擬斥力勢場法解決了人工勢場法中的局部極小問題。唐彪等[3]利用添加虛擬目標點來改進人工勢場法。Wei Guan等[4]利用變步長結合重構的勢場函數來逃離局部極小點。楊小菊等[5]利用模糊控制算法進行移動機器人的避障研究，將傳感器采集到的信息反饋給模糊控制器，進而不斷修正位姿進行避障。Amal Karray等[6]利用自適應模糊控制器實現移動機械臂的軌跡追蹤和避障。

針對人工勢場法常見的局部極小問題的解決方法大多集中在陷入極小問題后如何逃離，本文通過添加模糊控制器控制引力與斥力勢場權重系數可以避免陷入局部極小，規避該問題。

1 人工勢場法的原理

傳統的人工勢場法就是在笛卡爾空間中引入了引力勢場以及斥力勢場，引力勢場是由目標點對機械臂的吸引產生的，而斥力勢場是由障礙物對機械臂的排斥所產生的。在這兩個合勢場的共同作用下，機械臂到達目標點并實現了避障。設機械臂的當前位置是P=[x，y，z]，目標點的位置是Pg=[xg，yg，zg]，那么引力勢場的一般式如式(1)所示。

式(1)中ka表示引力勢場系數，Uatt就是引力勢場。

斥力勢場表示為式(2)所示。

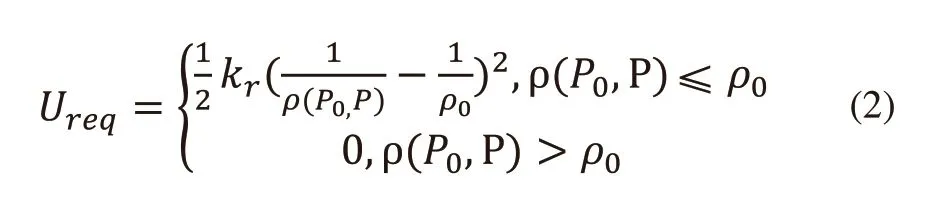
式(2)中kr是斥力場系數，ρ（P0，P）是障礙物到機器人的距離，ρ0是斥力勢場的影響距離，是一個常數。

2 改進算法

2.1 關節空間搜索

傳統的人工勢場法通常針對的是平面移動機器人，在二維空間中受引力和斥力的合力作用。但這里是針對機械臂的路徑規劃，而機械臂是強耦合以及在三維空間運動的。如果在三維空間進行路徑規劃就需要進行反解，這就大大增加了計算量，同時容易出現奇異點的問題。本文中是在關節空間進行的規劃。關節空間搜索方法如下：

1）設當前的關節位置為θ=（θ1，θ2，…，θn），n為機械臂關節數目。

2）設定步長為σ，遍歷每個關節角的相鄰位置,每個關節角都有3個位置，則總共有3n種組合方式。

在手術室內,由經管護士繼續以親切的語言和熱情的態度與其交流,與患者建立良好的護患關系,以減輕其因為環境改變而帶來的心理壓力。給患者介紹手術環境,手術過程,以及注意情況,多與患者溝通,適時給予安慰和鼓勵,及時解決患者的心理問題,提高患者對其自身疾病的認知程度和應對能力。消除患者對手術疼痛的恐懼感及焦躁的情緒,以積極平和的心態應對術后疼痛等問題,提高對治療的依從性。

3）計算每種組合的合勢能，最小的勢能所對應的關節角就是下一步的關節角位置。

4）如此循環計算，直至到達目標點。

在關節空間中搜索，將合勢場作為目標函數，機械臂就向著合勢場最小的方向運動，該方式規避了反解等問題。降低了計算的難度和強度。

2.2 勢場函數

針對人工勢場法中勢場函數中的參數引力與斥力勢場系數ka，kr不好確定的問題，這里對勢場函數進行了改進，確定了參數的選取。

引力勢能：

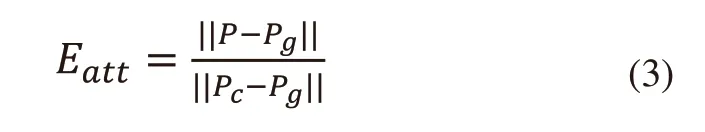
式(3)中P是機械臂末端的位置，Pg是目標點位置，Pc是機械臂末端初始位置。

斥力勢能：

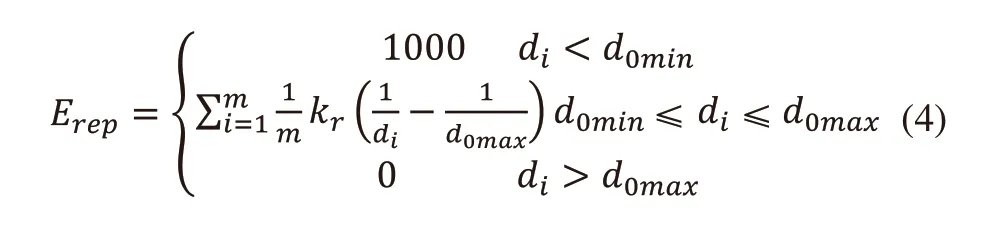
3 模糊控制器設計

這里設計了一個模糊控制器來控制勢場函數中的引力勢場權重系數Wa和斥力勢場權重系數Wr。該模糊控制器將機械臂與障礙物的距離以及該距離的變化率作為輸入，權重系數Wa，Wr作為輸出。如圖1所示。

圖1 勢場權重模糊控制器

引入權重系數后，合勢場就如式(5)所示。根據機械臂與障礙物的距離以及距離變化率，模糊控制器控制兩權重系數的大小。

輸入為障礙物與機械臂距離，其論域是[100，1000]，其模糊語言變量為['VN'，'N'，'M'，'F'，'VF']，距離變化率的論域為[-1，1]，模糊語言變量為['Negative'，'Zero'，'Positive']。圖2為機械臂與障礙物距離隸屬度函數，這里用的是三角形隸屬函數。圖3為機械臂與障礙物距離變化率隸屬度函數。

圖2 障礙物距離隸屬度函數

圖3 障礙物距離變化率隸屬度函數

輸出為引力勢場權重系數Wa和斥力勢場權重系數Wr。Wa其論域為[5，1 0]，模糊語言變量為['VS'，'S'，'M'，'B'，'VB']；Wr論域為[0，5]，模糊語言變量為['VS'，'S'，'M'，'B'，'VB']。圖4和圖5分別為Wa和Wr的隸屬度函數。模糊系統的Wa和Wr輸出曲面如圖6、圖7所示。

圖4 引力勢場權重系數隸屬度函數

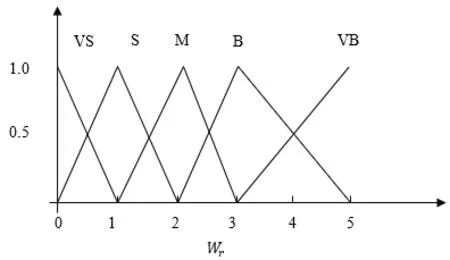
圖5 斥力勢場權重系數隸屬度函數

圖6 引力勢場權重系數輸出曲面

圖7 斥力勢場權重系數輸出曲面

該模糊控制器的規則如表1所示。本文的模糊推理采用Mamdani法，反模糊化采用了重心法。采用的是IFTHEN條件語言，共有3×5=15條模糊控制規則。

表1 模糊控制規則

4 仿真實驗

4.1 機械臂建模

這里用MATLAB進行了仿真實驗。選定的機械臂為kukaiiwa機械臂，如圖8所示。其DH參數如表2所示。這里仿真只用到該機械臂的前四個關節。

圖8 kukaiiwa機械臂

表2 kukaiiwaDH參數

圖9 機械臂前四個自由度DH參數模型

該kukaiiwa機械臂是七由度的，有肩部，肘部和腕部。這里只關注前四個自由度，腕部關節作為末端點。

式(6)、式(7)，式(8)中P，Pe，Ps分別是機械臂末端，肘部以及肩部的空間位置坐標。

4.2 局部極小問題

假設機械臂初始位置時θ=[0，0，0，0，0，0，0]，目標點的坐標為Pg=[400，400，400]，障礙物坐標為P0=[200，200，500]，d0min=100，d0max=300。首先對傳統算法的進行了仿真。圖10是傳統算法中機械臂的四個關節角位置圖。

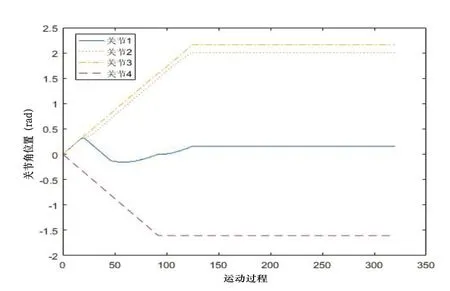
圖10 傳統算法機械臂四個關節角位置

由圖可以看出機械臂關節角保持不變，機械臂末端并為達到目標點。此時機械臂陷入了局部極小。同樣的任務對改進算法進行了仿真。關節角位置如圖11所示。

圖11 改進算法機械臂四個關節角位置

圖12是機械臂末端與目標點距離，由圖可以看出機械臂到達了目標點。機械臂與障礙物距離如圖13所示，可以看出機械臂與障礙物距離大于最小安全閾值d0min，機械臂實現了避障達點。

圖12 機械臂末端與目標點距離

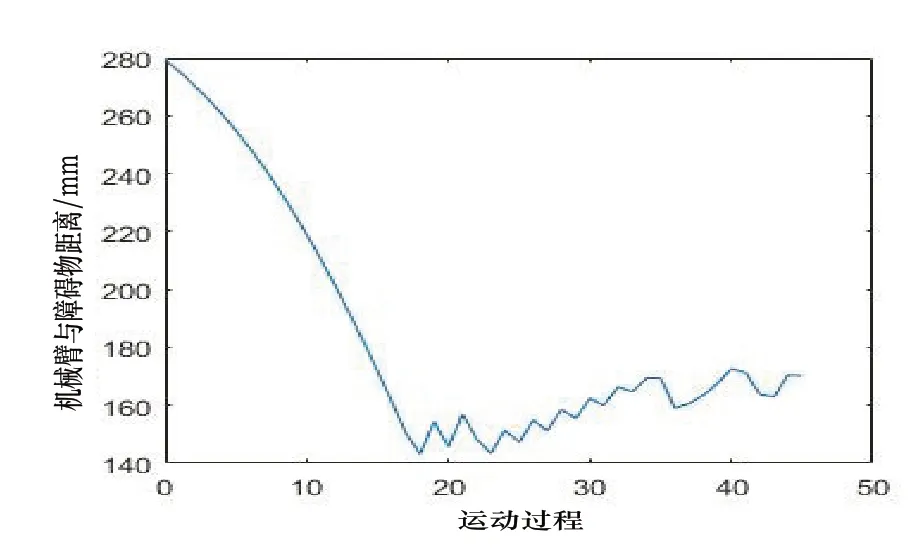
圖13 機械臂與障礙物距離

5 物理樣機實驗

這里使用了kukaiiwa機械臂進行了實驗驗證。如圖14所示，機械臂實現了避障達點運動。

圖14 kukaiiwa機械臂避障實驗

6 結語

使用模糊人工勢場法在關節空間進行避障路徑規劃，對原算法的勢場函數進行了改進，同時加入了權重系數，利用模糊控制器控制該參數，解決了局部極小問題。通過MATLAB仿真以及kukaiiwa機械臂的實驗驗證了方法的有效性。