研究分數(shù)的由來

□屈晶晶

研究背景

人類歷史上最早產(chǎn)生的數(shù)是自然數(shù)，它的出現(xiàn)給人們帶來了極大的便利，但是在日常的學(xué)習(xí)和生活中往往會出現(xiàn)不能正好得到整數(shù)的結(jié)果。例如這種情況：家里買來一個大西瓜，有4 個人分著吃，每個人吃這個西瓜的多少呢？這個結(jié)果就不是整數(shù)。所以，研究分數(shù)的由來，了解分數(shù)的應(yīng)用，能夠幫助我更好地解決學(xué)習(xí)和生活中的難題。

研究過程

1.畫圖

首先，分別找到三張不同形狀的紙片——長方形、正方形和圓，然后將這些紙片按照不同的方式平均分成不同的份數(shù)，我將其中的一份涂上顏色，最后用分數(shù)來表示被涂上顏色的一份是多少。

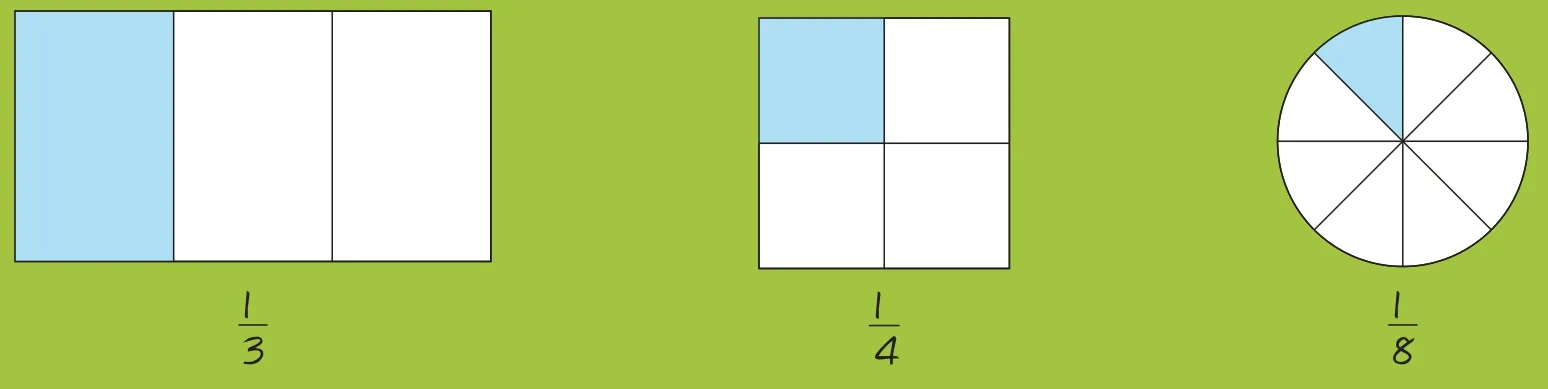
2.計算

我們都知道6÷3＝2，15÷5＝3，這些計算結(jié)果都是整數(shù)，那么2÷3 等于多少呢？大約在公元前的五世紀(jì)，中國開始出現(xiàn)把兩個整數(shù)相除的商看作分數(shù)的認識，也就是說這個表示兩個整數(shù)相除的商。

從上表可以看出，分數(shù)與除法的關(guān)系是緊密相連的，分數(shù)的分子相當(dāng)于除法里的被除數(shù)，分數(shù)的分數(shù)線相當(dāng)于除法里的除號，分數(shù)的分母相當(dāng)于除法里的除數(shù)，這個分數(shù)本身就是除法里的商。

3.分數(shù)的表現(xiàn)形式

古代是用算籌表示分數(shù)，在我看來就是用小棒來擺出分數(shù)，分子擺在上面，分母擺在下面。印度人沒有算籌就用阿拉伯?dāng)?shù)字表示，同樣的，分子在上，分母在下。后來，阿拉伯人用一條短橫線把分子和分母隔開，就成了我們現(xiàn)在用的分數(shù)。

研究結(jié)論

通過“分數(shù)的由來”這一課題的研究，我知道了分數(shù)的產(chǎn)生是為了更好更快地服務(wù)于我們的生活。……