基于改進模擬退火算法的采煤機滾筒調高優化研究

趙有生，賈 文，王強喜，盛長斌，閆孝姮

(1.山西焦煤集團投資有限公司，山西 太原 030024；2.山西焦煤集團嵐縣正利煤業有限公司，山西 呂梁 035200；3.遼寧工程技術大學 電氣與控制工程學院，遼寧 葫蘆島 125105)

目前采煤機智能化自動割煤已經成為綜采工作面的主要發展方向和發展趨勢，實現滾筒的快速和穩定的調高是實現采煤機智能化、無人化割煤的關鍵技術[1-3]。針對采煤機滾筒自適應調高，陳浩峰[4]等建立了滾筒調高關鍵元件閥控缸的數學模型，為以后調高控制策略的發展提供了研究基礎。張修榮[5]從電液比例控制系統出發建立了調高系統的傳遞函數，進一步使用了PID控制器對調高系統控制，這種方式雖然比開環控制更加穩定，但是沒有提及尋找最優的PID參數的方式。針對傳統閉環控制具有的不靈活、適應性差的缺點，趙麗娟[6]，等建立了滾筒調高的傳遞函數，進一步提出了基于模糊PID的采煤機調高控制策略，通過仿真證明了這種控制策略與傳統PID相比具有較好的平穩性和快速性。高永新[7]等利用MATLAB/simlink中的工具箱構建了采煤機調高控制系統的仿真模型，通過輸入不同的信號證明了模糊自適應PID比傳統PID 具有位置跟蹤性能好的優點。馮凱[8]等，使用以遺傳算法尋優后的PID參數構建了采煤機調高系統的PID控制器，結果表明使用這種優化后的參數的PID控制器，比傳統控制器具有響應速度快，跟蹤平穩性好的優點。但是，上述控制策略具有一定的局限性，模糊PID中的模糊控制經驗復雜，隸屬函數關聯性較高，且模糊控制器的設計依賴于現場的專家經驗。遺傳算法的局部搜索能力較弱且計算量大，往往需要多次尋優才可以得到局部最優的值。因此本文提出一種基于改進的模擬退火算法的采煤機滾筒調高控制策略，不僅具有傳統模擬退火算法的優秀的局部搜索能力，而且通過回火行為增強了算法的全局搜索能力，精準確定采煤機滾筒調高的PID參數，利于煤炭生產。

1 改進的模擬退火算法

1.1 傳統模擬退火的原理

模擬退火算法求解思想和過程與熱力學中固體熔融再凝固這一退火過程相類似，在工程中運用模擬退火算法尋優的基本原理是，將實際問題中要優化的目標函數作為模擬退火算法中的目標函數，將目標函數的解空間對應狀態空間，按照狀態產生函數隨機的產生解，根據接受概率選擇是否接受當前解為新解，逐步尋優的過程。

1.2 傳統模擬退火算法尋優的過程

1)初始化：給定初始溫度Tk(k=0)，隨機初始化解x0，退火系數λ，內外部中止條件，以及能量函數。

2)在當前溫度下，在當前最優解xk的鄰域內根據狀態產生函數隨機的產生新解x’；根據目標函數的函數值來判斷新解x’是否直接滿足優化條件，若是則用新解x’來替換當前解xk。若不是直接滿足則計算當前解是否在Metropolis準則決定的接受概率下，若在接受概率下，依然用新解x’來替換當前解xk。否則，舍棄掉新解。

3)根據內部循環中止原則判斷是否應該中止內部循環，常用的內部循環準則是：判斷在溫度T下是否達到了規定的迭代次數即鏈長L，或者滿足平衡條件。若滿足則轉到步驟(4)，若不滿足則跳轉到步驟(2)。

4)退溫過程：令k=k+1，Tk+1=λTk。

5)判斷是否滿足中止條件，若滿足則停止并尋優輸出尋優完成的KP、KI、KD，若不滿足則執行步驟(2)。

ITAE是常用的評價系統性能的指標，改變KP、KI、KD三個參數的值直接影響的是系統的性能，所以可以采用ITAE作為模擬退火算法的目標函數。其數學表達式為式(1)。可以看出ITAE的值越小說明選取的KP、KI、KD的值越合適。

1.3 模擬退火算法的改進

1)針對傳統模擬退火算法會產生重復的解，在第(2)步引入禁忌搜索(TS)的思想。即構建一個長度為L的禁忌表將每次產生的優秀的采煤機調高參數按隊列加入禁忌表中，若后面產生的采煤機調高參數在禁忌表中則返回重新生成，這樣可以有效避免采煤機調高參數的重復生成，加強了全局搜索能力。

2)針對模擬退火算法在溫度較低時難以跳出局部搜索的陷阱，在第(4)步中引入回火升溫的過程，即當溫度較低時適當的升高系統溫度，有利于算法跳出局部搜索的陷阱，得到最優采煤機調高參數。

3)針對模擬退火算法的效率問題，在第(5)步中引入一種新的中止尋優的方法，即當目標函數的值已經連續λ次不發生較大的變化則可以認為尋優已經完成，采煤機調高參數已經得到。

2 采煤機調高系統的傳遞函數

采煤機滾筒調高系統，主要由搖臂機構、截割滾筒、閥控缸、反饋機構和液壓控制回路來組成。采煤機調高系統實際上是一個電液比例控制系統，根據文獻[5]，若忽略活塞運動過程中的黏性阻尼系數和外部干擾，可以得到采煤機調高系統的傳遞函數為：

式中，A1和A2分別為調高油缸內部活塞左右兩腔有效面積，m2；Kq、Kf分別為反饋系數和等效系數；ωh和ξh系統阻尼比和固有頻率系數。本文選取的采煤機的參數如下：2A1-A2=15×10-3/m2、ωh=163/rad·s-1、Kq=2/m2·s-1、Kf=1.5。帶入式(2)可得采煤機調高系統的傳函為：

3 仿真與驗證

3.1 改進模擬退火算法的驗證

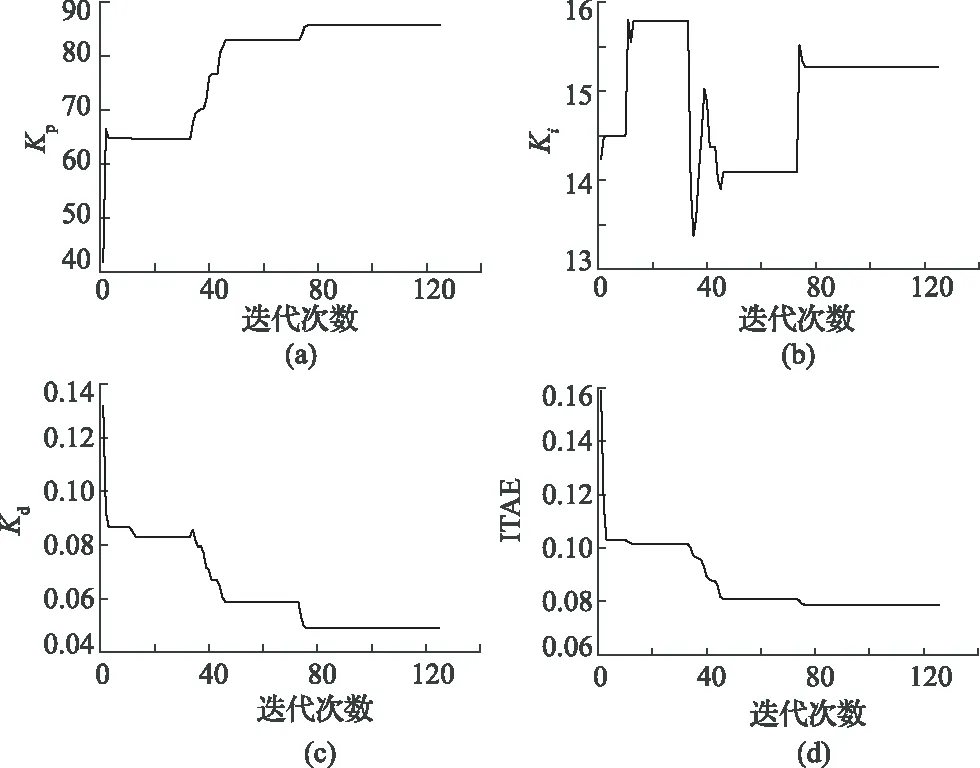
圖1 傳統模擬退火算法各參數值隨著迭代次數的變化

使用MATLAB分別編寫傳統模擬退火尋優算法和改進后模擬退火算法的程序，給定相同的初始參數(包括：初始溫度T0=150，Metropolis鏈長L為200，降溫系數γ=0.95，中止溫度Te=1。)同時設置改進的模擬退火特有的參數如下：(回火系數λ=0.5，溫度降低φ=30次解不變就中止尋優)。針對前文提出的采煤機調高系統的傳函，編寫相同的ITAE計算函數，根據系統整定的經驗可以選取KP、KI、KD的取值范圍分別是[0，90]，[0，20]，[0，0.15]。傳統模擬退火算法和改進的模擬退火算法在尋優過程中KP、KI、KD最優解和ITAE的最小值隨著迭代次數的變化過程分別如圖1中的(a)、(b)、(c)、(d)、和圖2中的(a)、(b)、(c)、(d)所示。經過對比可以看出雖然改進前后的算法都能夠實現對KP、KI、KD的參數的尋優，但是改進后的模擬退火算法尋優得到的參數能夠使的ITAE的值達到最小為0.02，而傳統模擬退火算法尋優得到的參數值僅能夠使ITAE的值達到0.08。這表明傳統模擬退火算法陷入了局部尋優，同時也說明前文提到的針對模擬退火算法的改進措施能夠使模擬退火算法有效的避免陷入局部尋優，得到全局最優解。

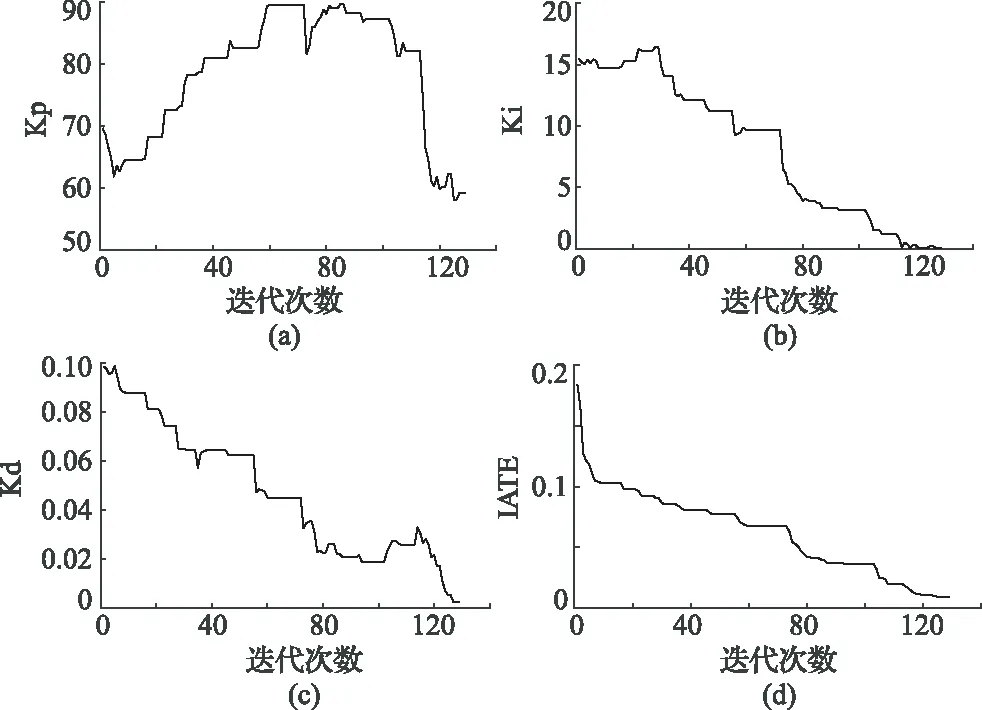
圖2 改進后模擬退火算法各參數值隨著迭代次數的變化

3.2 調高系統的仿真驗證

由于任何優化算法都是理論上可以達到最優，所以為了避免誤差，在進行多次仿真后取平均值得到最優值為KP=59，KI=0.1，KD=0.05。使用優化后的參數結合simulink中的仿真工具箱構建系統的仿真框圖。仿真框圖如圖3所示。

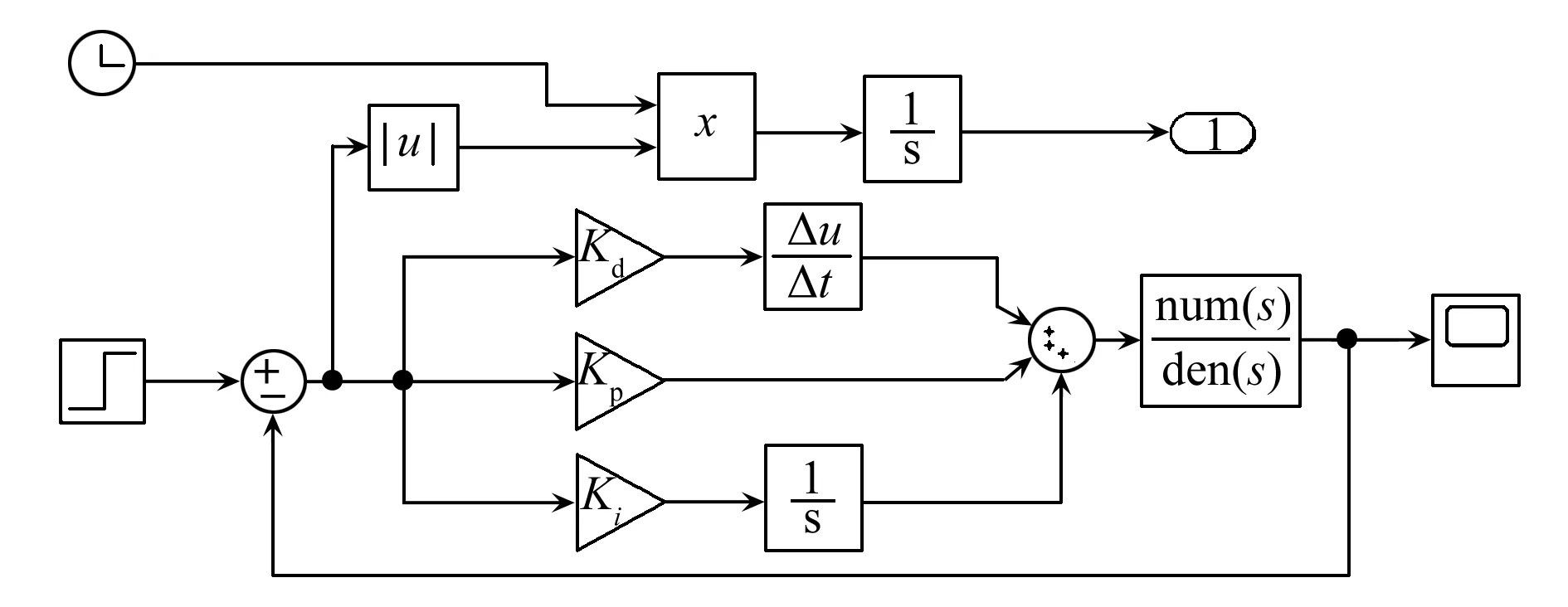
圖3 系統仿真框圖

在第6s處給定幅值為1持續1s的擾動來驗證其魯棒性，其輸出曲線如圖4所示，從圖4中能夠看出，系統受到擾動后用了0.1s的時間恢復到穩定水平，表明系統對擾動有著較好的抗性，魯棒性強。同時可以看到系統還具有較小抖震，表明系統具有良好的穩態特性。

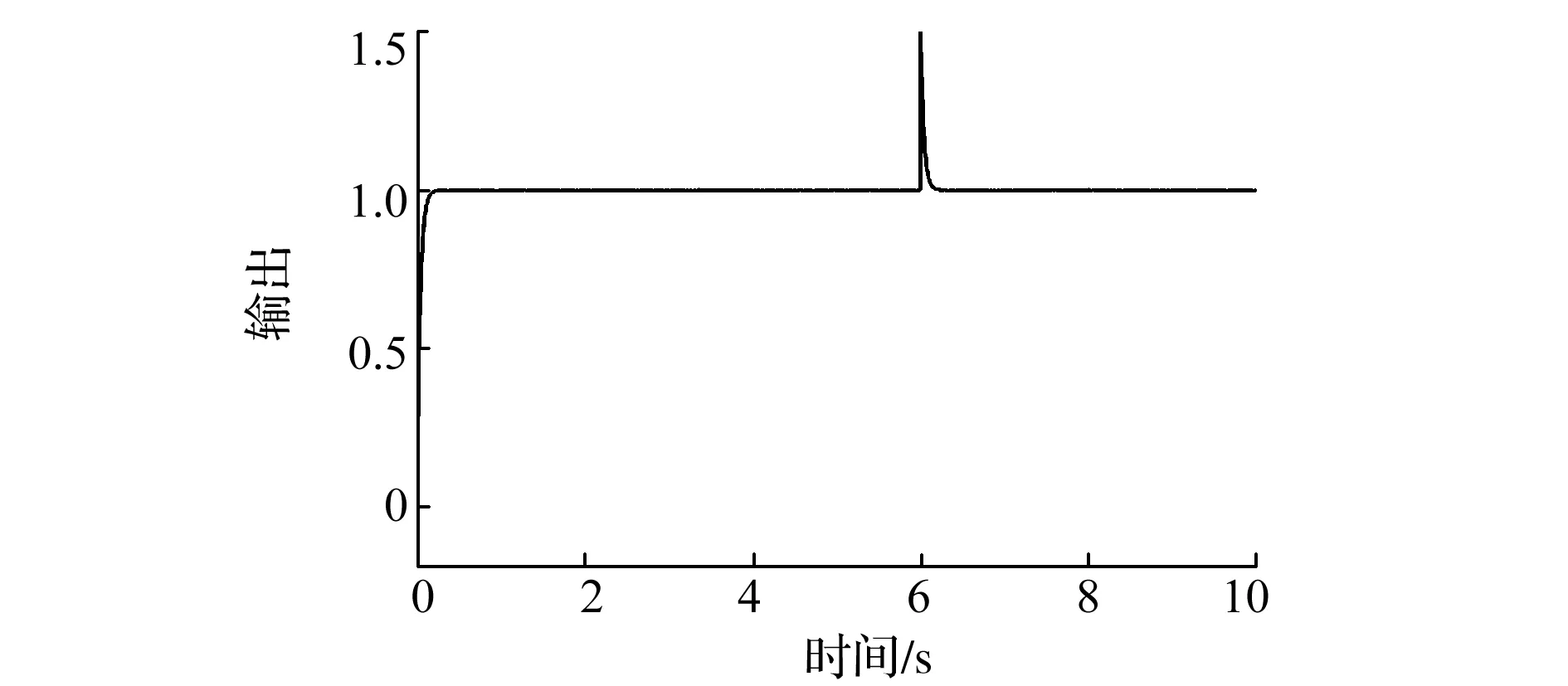
圖4 擾動仿真結果圖

分別給系統輸入幅值為1、周期為2、占空比為50%的方波信號和幅值為1、角速度為10πrad/s、的正弦信號來驗證系統的信號跟蹤特性，設置仿真時間10s和5s。仿真結果分別如圖5、圖6所示，從圖中可以看出系統能夠較好的跟蹤不同的輸入信號，表明系統有較好的跟蹤特性。

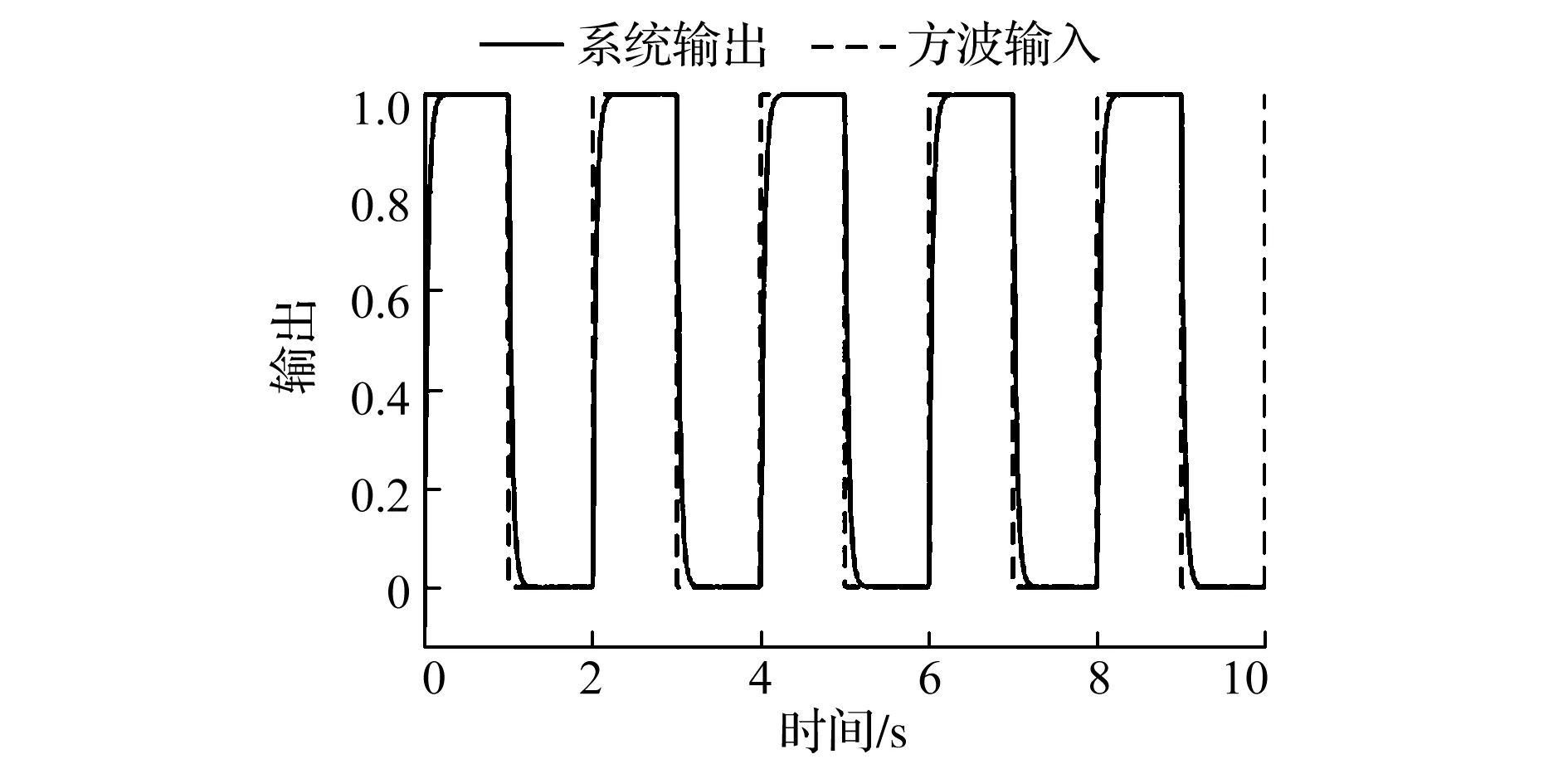
圖5 方波信號的跟蹤仿真

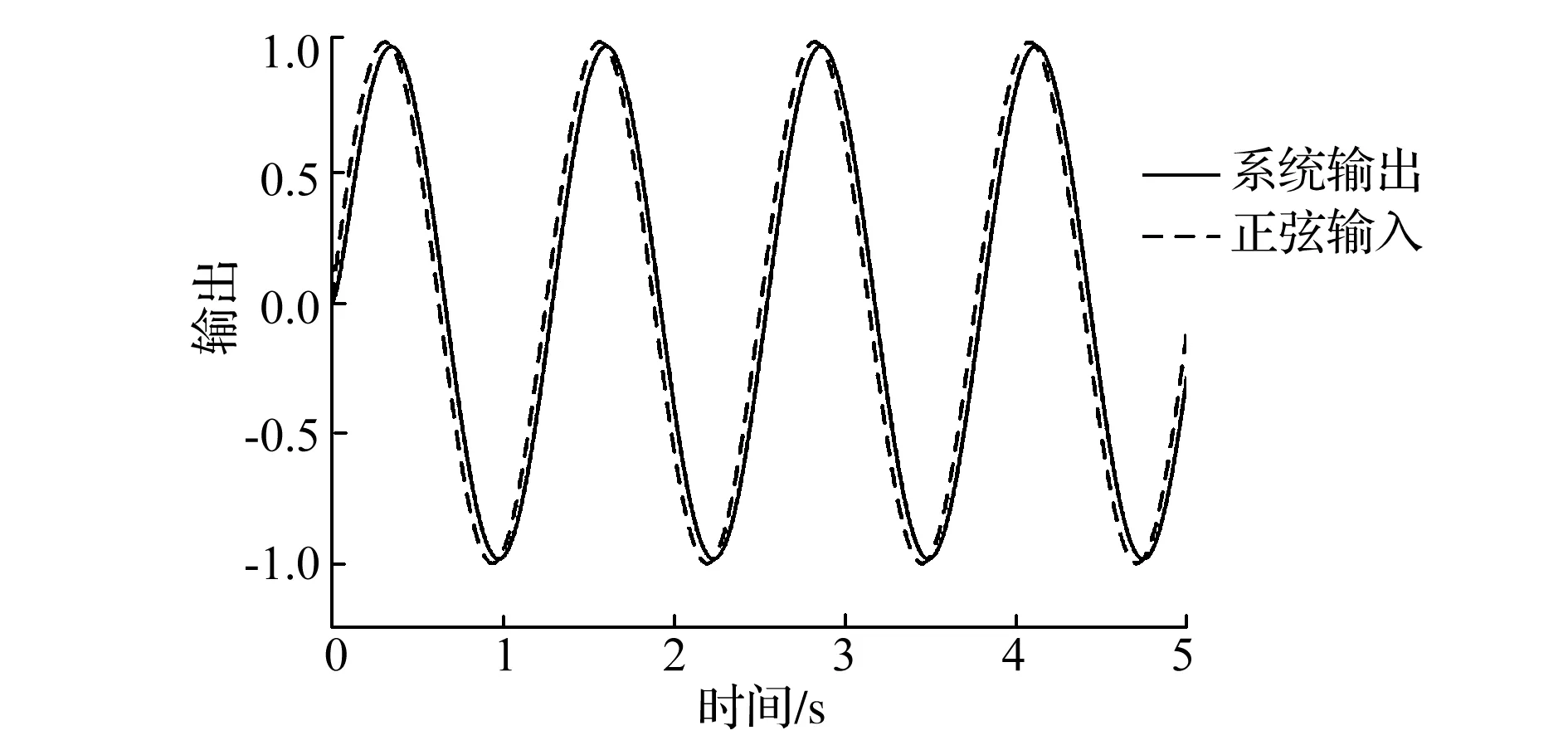
圖6 正弦信號的跟蹤仿真

4 結 論

1)根據模擬退火算法理論前提，在傳統的模擬退火算法的基礎上引入了禁忌搜索、回火退火的思想。以采煤機調高系統的ITAE指標作為目標函數，結合MATLAB程序尋優計算了采煤機滾筒調高系統PID控制器的參數。

2)以采煤機調高系統的傳函為基礎，構建了采煤機滾筒調高系統的仿真模型，研究并分析了采煤機滾筒調高系統的跟蹤特性和魯棒性。通過對不同信號的跟蹤，仿真結果表明設計的控制器穩定有效。為采煤機滾筒調高實現準確跟蹤目標路徑提供了一種有效途徑。