基于多元退化的航空機電系統的剩余壽命預測

劉敏 劉長生

摘要：當前，基于競爭故障的航空機電系統剩余壽命預測模型的研究較多，而其中以性能退化和突發故障并存為基礎的模型建立備受關注。這一方法以狀態監測數據為依據，分析了性能退化故障和突發故障的關聯度，并通過對參數退化率的監測分析預測系統的使用壽命，最后建立了航空機電系統壽命變化趨勢的模型。該模型的建立有利于提高航空機電系統剩余壽命預測的準確率，能夠為機電系統的維修提供科學的參考。

關鍵詞：機電系統;性能退化;剩余壽命

中圖分類號：TP311 文獻標識碼：A

文章編號：1009-3044（2019）31-0229-02

對航空機電系統剩余壽命的預測能夠為飛機的飛行提供一定的依據，能夠有利于提高飛行的安全性和穩定性，因而受到了極高的重視。關于航空機電系統剩余壽命的研究也較多，如故障預測、故障維修等，這些方法都以狀態的檢測信息為基準，所采集到的信息較為單一、片面，無法準確預測航空機電系統的剩余壽命。也就是說，關于航空機電系統剩余壽命的預測多集中在單一的角度而開展，退化量的多元化沒有受到應有的關注。因此，筆者嘗試通過多個退化模式對航空機電系統的故障進行判斷，并判斷系統的剩余壽命。

1基本思路

根據機電系統剩余壽命預測所需要的數據，本研究選擇了相關參數，隨后建立了以性能退化為基準的故障模式，重新設定了新的參數，然后分析了混合威布爾模型對突發故障的預測作用，并對其進行了預測。然后，從多元退化的角度建立了退化故障和突發故障的剩余壽命預測模型。

2獲取數據

航空機電系統剩余壽命的預測需要有豐富的、有效的參數支持，而如何獲取參數也成了當前學界研究的熱點和難點問題。常規來講，航空機電系統會產生兩類數據，一類是性能退化數據，另一類是突發數據。性能退化數據主要是通過系統狀態的檢測獲得的，而狀態檢測數據具有樣本小、緯度高的特點。為了更好地利用這些參數，在使用前要先對其進行優化處理：首先要進行篩選，選出有效數據，剔除無效數據。然后將收集到的參數融合到一起，并通過貝葉斯工具分析機電系統的退化情況。另外，突發故障具有突發性、緊急性的特點，突發故障的數據少，因此，多使用普遍反映故障發生率高的數據作為突發故障數據使用。

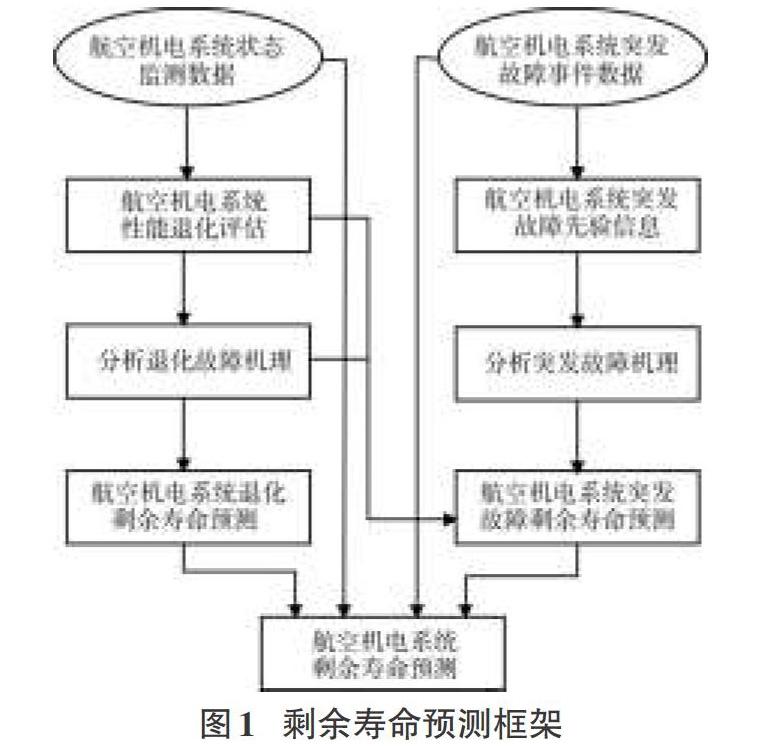
3航空機電系統剩余壽命預測的基本框架

為了提高對航空機電系統剩余壽命的預測準確度，本研究建立了以性能退化故障數據和突發故障數據為基礎的競爭故障影響下的剩余壽命預測框架。詳見圖1。

4以貝葉斯線性模型為支撐的航空機電系統性能退化預測的模型

首先，假設航空機電系統的性能退化的相關參數已經被提取，然后再構建航空機電系統性能退化預測的模型。設參數和退化程度的關系為0，將矩陣表示為u=（u1，u2，……vuk），其中k是個數，vk是n行列矢量，n為觀測的次數。那么能夠將狀態檢測參數和性能退化參數表示為：U=V·θ+e，e～N（O，∑）。由于航空機電系統的狀態檢測數據具有不穩定性和隨機性的特點，本研究選擇使用了貝葉斯線性模型對檢測數據進行處理，以此降低數據的不確定性，從而提升預測的精準度。根據有關研究和筆者的實際經驗，假設航空機電系統的檢測參數呈逆高斯分布狀態，通過公式能夠計算出航空機電系統狀態監測數據的期望和方差值，然后使用M=E【（θ-θ）（θ-θ）T計算后驗期望值。

航空機電系統的性能退化數據多表現為平穩狀態，因此，本研究使用線性退化模型對航空機電系統各部分的狀態參數的退化率進行描述，并使用退化率預測系統的使用壽命。用s（t）表示t時間段內的退化累積量，用ε（t）表示噪音函數，用來衡量t課時的噪音數據，公式可表示為s（t）=Ф+βt+ε（t）。

根據有關研究和實際經驗，航空機電系統檢測數據呈正向分布，其均值用u表示，方差用δ表示。使用貝葉斯法能夠得到不斷融合的監測參數，并建設系統的剩余壽命為T，性能退化的范圍用D表示，則能夠將第l個觀測點的預測壽命表示為S（T+t）=D。

在得到新的檢測數據之后，將數據帶入U=V·θ+e，e-N（0，∑）之中就能夠得到機電系統的退化程度，并能夠得到系統的退化率，然后使用貝葉斯法預測航空系統在未來一段時間段內的退化率。并假設航空機電系統退化率呈正態分布，并表示出后驗期望均值、方差和區間等。然后按照s（T+I）=D這一公式，使用蒙特卡洛仿真法計算航空機電系統性能退化故障的剩余壽命。

5以混合威布爾模型為支撐的航空機電系統突發故障預測的模型

1）混合威布爾模型

由于航空機電系統的性能退化故障數據類型多樣，但突發故障數據較少，筆者就選用了威布爾分布對航空機電壽命預測中的突發故障數據進行處理，以更加充分地利用這些數據。我們使用y來表示機電性能退化和壽命分布變化的關系。由于航空機電系統性能退化具有多種類型，本文選用混合威布爾模型的可靠性更高。設航空機電系統是由兩個圍而不分布構成，其中的一個權重概率為p，那么機電系統突發故障的可靠度就可以表示為R（t）=pxexp[t/a+（1-p）xexp]。然后結合機電系統的特點，根據性能退化率的上下限建立了威布爾模型，系統可靠性的計算如下：R（t）=pxexp[-t/a]+（1-p）xexp[-t/a]，所得的結果可靠度更高。同時，在代人公式計算的航空機電系統性能退化率的上下限，能夠計算對應的威爾分布形狀參數，建立了混合威爾分布模型，所得到的權重p和（1_p），另外還需要驗證分布逆Ga（a，b）的超參數。

2）逆Ga（a，b）的超參數先驗和后驗參數學習

通過計算我們能夠知道參數a的均值和方差，尺度參數能夠表示為a=t/ln（1/Ro）]，超參數a和b能夠得到a=E²/a²，b=E（a）/a2，通過搜集突發故障檢測數據，t為突發故障發生，n為突發故障的樣本數，在學習后的后驗參數a和b表示為a=a+t，b=+n。

3）Beta（w，n）超參數先驗和后驗參數的學習

分布參數的先驗分布為叮π（p）=β（p，w，n），一般情況下，我們將Pn設為0.5，然后對數據和超參數關系w/w+n=pn，然后就可以將先驗分布和后驗分布參數表示出來，即w=（w-1）/B（w，n），n=（n-1）/b（w，n）。通過這一公式，我們能夠準確地表述出來先驗分布、后驗分布超參數兩者之間是如何相互影響的。

6實例分析

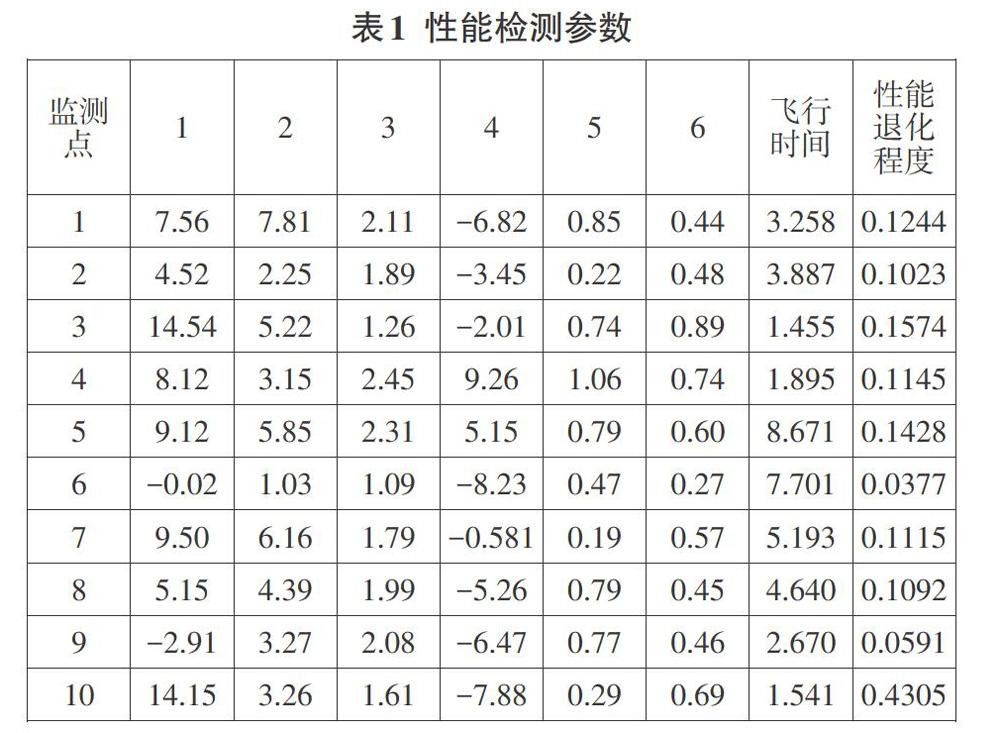
為了更好地驗證模型的有效性，我們選取了航空機電系統中具有代表性的系統為例，根據系統的主要檢測參數，采取了檢測時刻的起飛時間，選取10個監測點作為樣本，使用蒙特卡洛仿真方法計算航空發動機性能退化程度，并分析了其閾值的準確度等相關數據。

從表1中我們能夠得到10個監測點的檢測參數，并能夠計算出性能退化值和實際退化值的誤差低，利用前文中的計算公式能夠得到航空發動機系統性能退化乘0余壽命。

通過表1中對發動機的3此檢測和維修參數，我們能夠得到突發故障的先驗值為0.95，然后計算相關參數，并使用蒙特卡洛方法預測航空發動機系統突發故障壽命本實驗以R=0.90作為可靠度閾值，設發動機系統的性能退化故障剩余壽命為TP，突發故障的壽命Ts，取它們的最小值，計算結果如下：每次飛行時間分別為1708、4739、5594，每次突發故障剩余壽命的預測值分別為6026、2922、2113，剩余壽命的預測值分別為5872、2822、2113，R可靠閾值分別為-2.65，-1.62，-1.02。最后得到實際飛行時間為2185小時，整體結果誤差率小于5%，說明本方法有效，能夠用于航空機電系統剩余壽命的預測。

7結束語

本研究以性能退化故障和突發故障為基礎建立了航空機電系統剩余壽命預測的模型，這一方法實現了對狀態檢測數據的全面、有效使用，合理評估了性能退化故障和突發故障的相關度，較為準確地描述了機電系統壽命變化的趨勢，使航空機電系統剩余壽命的預測更加準確，為機電系統復雜裝備的制造和檢測奠定了堅實的理論基礎。