一種基于動態規劃法的關鍵路徑算法

詹澤梅

摘要：數據結構是計算機及其相關專業的一門重要專業課。在數據結構課程中，關鍵路徑是一個難點問題。本文首先概述了關鍵路徑問題，接著介紹了動態規劃法，分析其求解關鍵路徑的可行性，最后重點描述了采用十字鏈表存儲有向圖時的一種基于動態規劃法的關鍵路徑求解算法。

關鍵詞：關鍵路徑;動態規劃法;十字鏈表;AOE-網

中圖分類號：TP311 文獻標識碼：A

文章編號：1009-3044（2019）31-0215-03

1關鍵路徑

有向無環圖可用于描述一項工程的施工流程。在有向無環圖中，既可用頂點表示子工程（又稱活動），也可用有向邊表示子工程。當用有向邊表示子工程時，邊上的權值可表示完成子工程所需的時間、價錢等信息。這種邊表示子工程活動的有向無環圖就稱為AOE-網（ActiviIy On Edge），即邊表示活動的網。在AOE-網中，有且僅有一個人度為零的頂點，它稱為源點，代表工程的開始點;有且僅有一個出度為零的頂點，它稱為匯點，代表工程的結束點。

對于一項工程，人們通常要估算完成工程所必須的最短時間。當在計算機中用AOE-網描述工程施工流程時，完成工程所必須的最短時間就等于AOE-網中源點到匯點最長路徑的長度。此處路徑長度是指路徑上各活動持續時間之和，即各有向邊上的權值之和。路徑長度最長的路徑叫作關鍵路徑。估算整個工程完成所必須的最短時間，實際上就是要求AOE-網中的關鍵路徑。

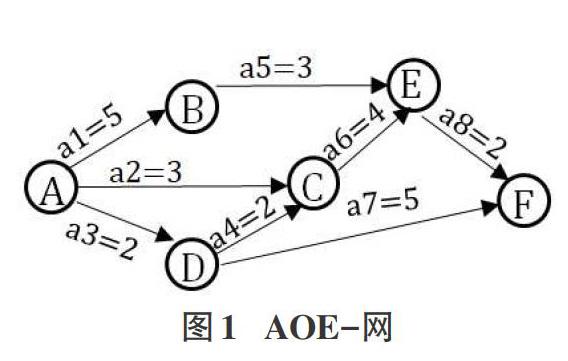
例如，圖1是一個AOE-網，它表示該工程可分為8個子工程活動。活動之間的施工先后關系是：工程一開始就可執行活動a1、a2、a3，活動a1完成后可開始執行活動a5，活動a3完成后可開始執行活動a4、a7，活動a2、a4完成后可開始執行活動a6，活動a5、a6完成后可開始執行活動a8，活動a7、a8完成后則整個工程完成。有向邊上的權值表示完成活動所需要的時間。頂點A是工程開始點（源點），頂點F是工程結束點（匯點）。完成該工程所需要的最短時間等于源點A到匯點F的最長路徑的長度。此AOE-網的最長路徑有兩條：ABEF和ADCEF，路徑長度為10，即完成整個工程的最短時間是10。這兩條路徑都是關鍵路徑。

2動態規劃法

動態規劃法是求解多階段決策最優化問題的一種常用方法。它所解決的問題需要滿足最優性原理。最優性原理簡單地說就是原問題的最優解由各個子問題的最優解構成。

關鍵路徑問題就是求AOE-網中源點到匯點的最長路徑，假定AOE-網的源點s到匯點t的最長路徑是s，x1，X2，…，Xp，t，則路徑s，x1，X2，…，Xp一定是源點s到頂點Xp的最長路徑。可用反證法證明關鍵路徑問題滿足最優性原理。如果路徑s，x1，x2，…，Xp不是源點s到頂點xp的最長路徑，存在另一條路徑s，Yl，Y2，…，Xp的長度大于路徑s，x1，x2，…，xp的長度，則路徑s，Y1，Y2，…，Xp，t的長度就大于路徑s，x1，X2，…，Xp，t的長度，這就與最初的假設“假定AOE-網的源點s到匯點t的最長路徑是s，x1，X2，…，Xp，t”相矛盾。所以關鍵路徑問題滿足最優性原理，可用動態規劃法求解。

動態規劃法將待求解問題分解成為若干個相互重疊的子問題，每個子問題對應決策過程的一個階段。該方法的求解過程通常可分為三個階段：劃分子問題、設定動態規劃函數、計算各個子問題并填寫表格。

3基于動態規劃法的關鍵路徑算法

3.1算法分析

動態規劃法求解問題時首先是劃分子問題。對于關鍵路徑問題如何劃分子問題呢？假設我們用Cxy表示有向邊上的權值，用Dis（s，v）表示源點s到頂點v的最長路徑長度。假設頂點u是頂點v的前驅頂點，則源點s到頂點v的最長路徑長度應為Csv和Dis（s，u）+Cuv中的最大值。即有以下等式成立。

由于源點s到頂點v的最長路徑與源點s到頂點v的前驅頂點u的最長路徑相關，所以子問題可設定為求源點到某頂點的最長路徑。動態規劃函數可使用上述等式。

動態規劃法的第三個步驟是計算各子問題并填表。此問題中就是要計算源點到各頂點的最長路徑。對于AOE-網中的各頂點，應按什么順序求解子問題呢？顯然前驅頂點的最長路徑應先求，所以應按照圖中有向邊指示的先后順序求各頂點的最長路徑，對于沒有先后順序的頂點可按任意順序求解。換句話就是要按圖中頂點拓撲有序序列中的先后順序求解源點到各頂點的最長路徑。

3.2圖的存儲表示

關鍵路徑算法的設計與圖的存儲結構密切相關。本問題中的有向圖如何存儲呢？由于在求源點到各頂點的最長路徑時，要按拓撲有序序列中的頂點順序求，那么就要對有向圖中頂點進行拓撲排序。在拓撲排序過程中，需要知道從各頂點出去的有向邊（弧），所以在圖的存儲結構中，應能方便找到從各頂點出去的弧。又由于源點到某頂點v的最長路徑與源點到v的前驅頂點的最長路徑相關，所以在圖的存儲結構中，要能方便找到任意一頂點的前驅頂點。十字鏈表存儲結構能很好地滿足這兩個要求，所以我們以十字鏈表作為本問題中圖的存儲結構。圖1所示有向圖的十字鏈表存儲結構如圖2所示。

3.3關鍵路徑算法

求關鍵路徑之前，首先要求出AOE-網的一個拓撲有序序列，假設用數組TopoV存儲拓撲有序序列中各頂點的位置下標。可按拓撲排序的方法求TopoV數組值。求解步驟如下：（1）找AOE-網中入度為0的頂點并存儲在數組TopoV中;（2）刪除以該頂點為弧尾的弧。重復執行（1）（2）兩步，直至找不到人度為0的頂點為止。

然后按算法1求AOE-網的源點到各頂點的最長路徑信息，最后按算法2輸出關鍵路徑和其長度。

算法1中MaxLenV數組存儲源點到每個頂點的最長路徑信息，其中MaxLenV[i1記錄源點到拓撲序列中第i+1個頂點的最長路徑信息，該頂點在有向圖的十字鏈表的vertices數組中的位置下標為TopoV[i]。頂點的最長路徑信息類型定義如下：

4總結

動態規劃法是求解最優化問題的一種常用算法設計技術。關鍵路徑問題的解滿足最優性原理，因此可用動態規劃法求解。本文在有向圖采用十字鏈表存儲方式下，設計了一種基于動態規劃法的關鍵路徑算法，該算法能正確的輸出源點到匯點的關鍵路徑及其長度。