帶參數學習的引導信號迭代學習控制方法
黃靜, 鄭華義, 李宏, 李國岫, 邱成
(1.北京交通大學 機械與電子控制工程學院, 北京 100044; 2.北京精密機電控制設備研究所, 北京 100076)
0 引言
在航空航天領域中,飛行器空氣舵的主要作用是控制飛行器的飛行姿態以及調整與改變飛行軌跡,其性能好壞直接影響飛行器的控制精度和穩定性。
空氣舵負載模擬器是空氣舵的重要地面試驗設備,用于模擬空氣舵在飛行過程中所承受的載荷,為空氣舵地面試驗提供可靠的試驗保障和技術支持。隨著我國航天和國防事業的大力發展,對飛行器提出了更高的要求,研究能夠精確復現飛行過程中力學條件的空氣舵負載模擬器勢在必行。而空氣舵負載模擬器在加載試驗中,會經常加載一些連續性、周期性負載,例如正弦信號、三角波信號、方波信號等。在加載過程中,除了加載系統的運動以外,空氣舵本身也會進行獨立的運動,二者運動是通過某些連接件耦合在一起的,因此給加載端控制帶來了極大的挑戰和難度。
本文研究的負載模擬器結構示意圖如圖1所示。從圖1中可以看出,加載系統和承載系統(空氣舵作動器)通過搖臂連接在一起,在空氣舵作動器獨立運動過程中,需要加載系統加載上所要求的模擬載荷。針對空氣舵負載模擬器所加載的負載具備周期性特點,期望找到一種帶有學習能力的智能型控制方法,以適應空氣舵地面負載試驗的要求。
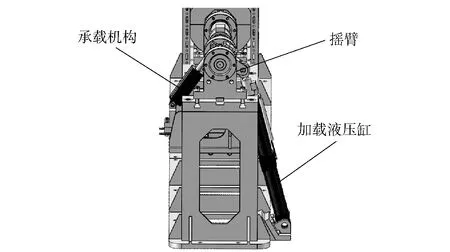
圖1 系統結構示意圖Fig.1 Schematic diagram of load simulator structure
在控制領域中,日本學者Uchiyama[1]最早于1978年基于迭代學習思想提出迭代學習控制(ILC)方法,隨后在1984年Arimoto等[2]正式提出該方法的理論框架并發展至今,如今迭代控制方法依然是智能控制領域的一個重要研究領域[3-6]和研究熱點[7-11]。
但是在ILC理論中,雖然理論上能夠證明其控制誤差最終收斂,但是對中間過程的誤差卻沒有限制和要求。而在實際工程應用中,即使誤差最終收斂,若是中間過程的誤差過大,也是不能接受的[12]。將傳統ILC方法應用于空氣舵負載模擬器的液壓控制系統中,嘗試跟蹤一個正弦信號,其系統輸出如圖2所示。
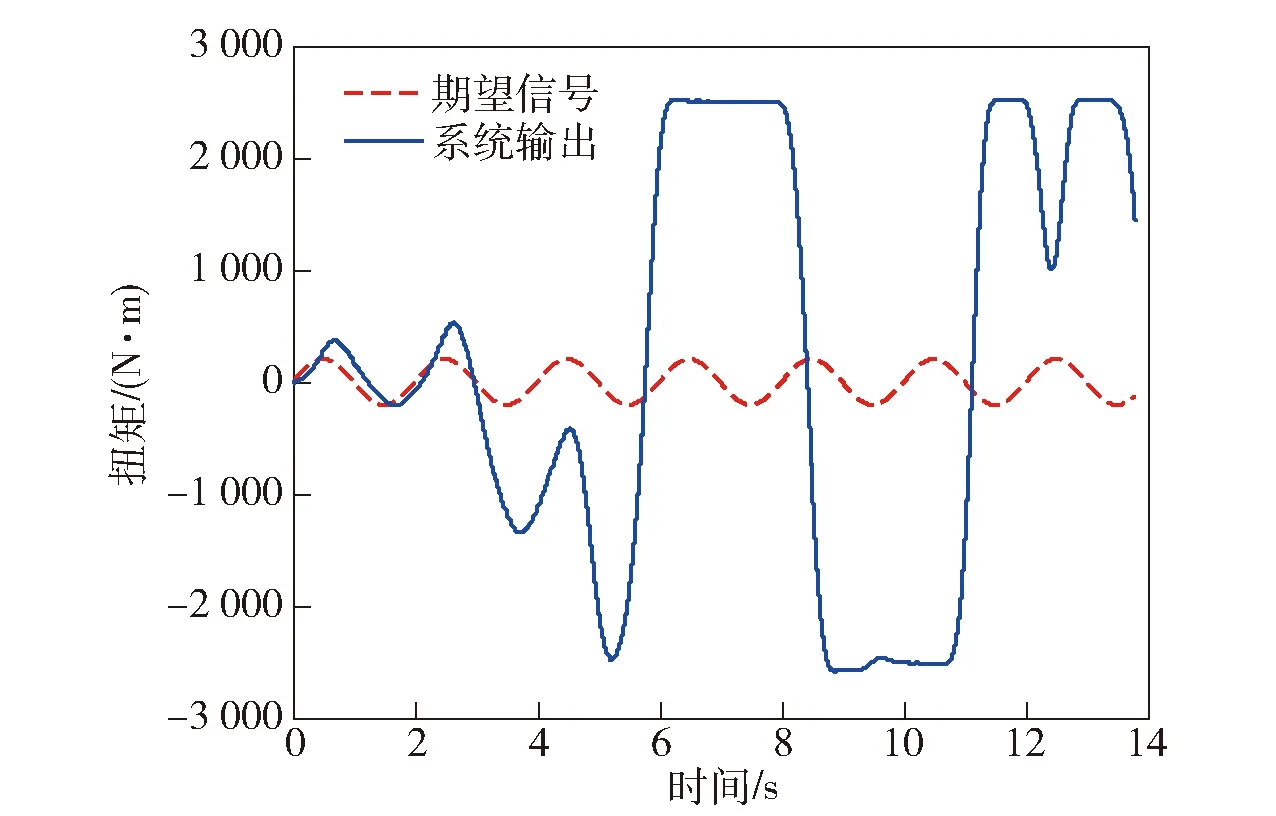
圖2 傳統迭代學習實際系統輸出Fig.2 Traditional iterative learning output in real system
從圖2中可以看出,系統在第2個周期后,誤差越來越大,系統逐漸失控。究其原因,主要有兩點:一是迭代學習控制理論中,一般都要求或假設每個周期的初始狀態是嚴格一致的,但是這一點在實際系統中很難做到;二是因為實際控制系統中,輸入信號和輸出信號之間存在一定的相位延遲,傳統ILC一般都未考慮相位因素的影響,在實際應用過程中,相位延遲也會對“經驗學習”有重要影響。
針對以上問題,本文嘗試保留ILC的優點,即智能性和實現簡單性,提出部分改進,希望解決傳統迭代控制方法中中間過程誤差較大、系統不受控的問題,同時使得新的ILC方法具備更快的收斂速度和更好的控制效果。
1 引導信號ILC方法的提出
控制系統一般有多種數學表示方法,若采用狀態方程表示方法,則離散的控制系統可以寫為(1)式的形式:
(1)
式中:k=1,2,3,…表示迭代次數;xk(t)、uk(t)、yk(t)分別表示系統第k次的狀態向量、輸入向量和輸出向量;xki(t)表示第k次迭代時系統的第i個狀態;A、B、C為系統的系數矩陣。
傳統ILC方法表達式如(2)式所示:
(2)
式中:ek(t)為系統第k次迭代的控制誤差向量;yd(t)為系統的期望信號向量;f(·)函數代表某種迭代學習律。
利用誤差向量ek(t)和輸入向量uk(t),通過設計或構建的學習律,便可以產生第k+1次的輸入向量uk+1(t)。從(2)式中可以看出,傳統ILC的學習對象是系統的輸入信號。為了解決系統控制過程中不受控的問題,結合傳統比例、積分、微分(PID)控制方法,提出一種新的控制信號即引導信號。讓系統的跟蹤信號不再直接跟蹤期望信號,而是跟蹤引導信號,迭代學習的對象也不再是輸入信號,而是引導信號。由引導信號和系統反饋輸出信號形成閉環PID控制,便能解決之前系統的不受控問題。
系統的引導信號ILC方法可以表示為如下形式:
(3)
式中:rk(t)為系統第k次迭代的引導信號;p為系統PID控制中的比例系數;L為N×N階迭代學習增益矩陣,N為一個周期內的采樣次數。
該方法應用于實際系統中,系統的輸出與傳統ILC的輸出對比圖如圖3所示。從圖3中可以看出,采用引導信號ILC方法以后,系統不再出現失控的情況,并且控制效果隨著迭代學習過程的進行逐漸得到改善。表明在引導信號ILC方法的作用下,系統不僅具備了學習的智能特性,并且解決了中間過程不受控的問題。
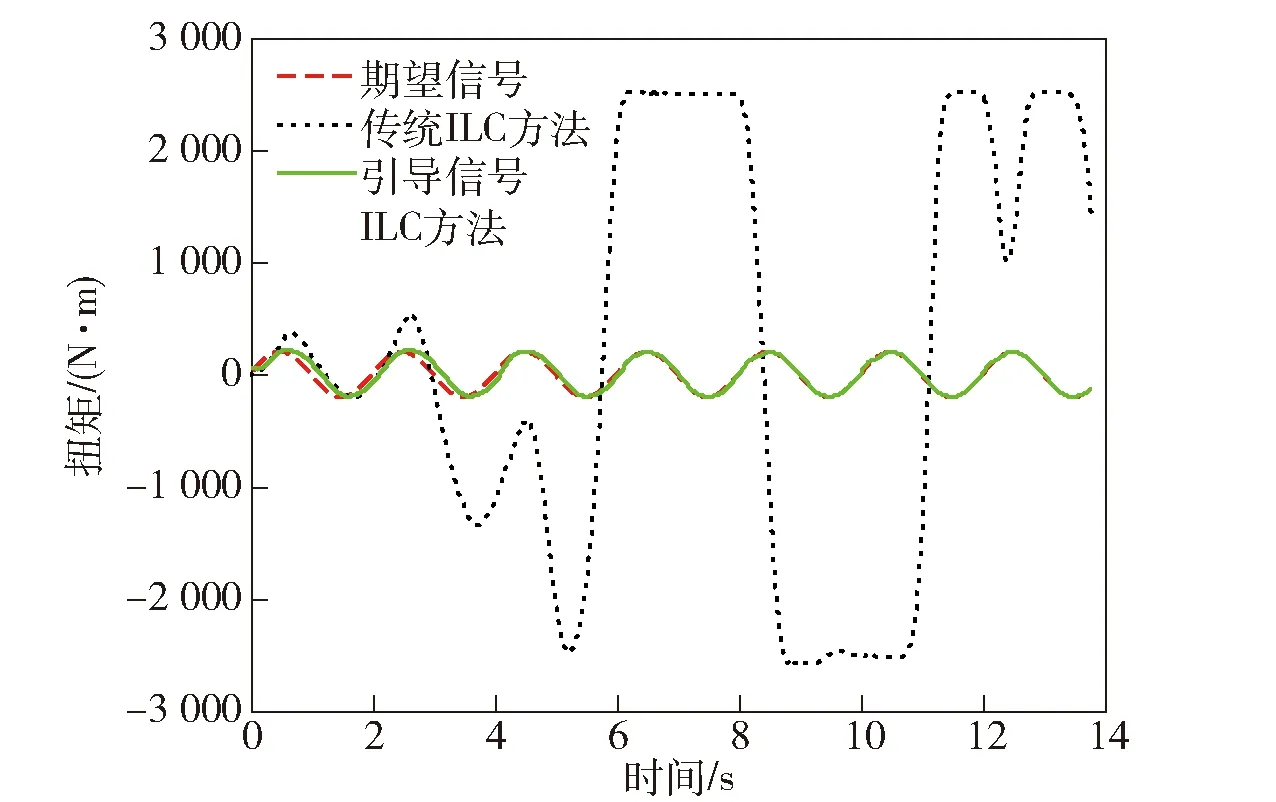
圖3 引導信號ILC實際控制效果Fig.3 Actual control effect of guiding signal iterative learning control algorithm
2 引導信號雙重學習控制方法的提出
(3)式中控制方法中的學習參數L為一個固定參數,為了提高學習效率,使控制系統具備更快的收斂速度,考慮針對學習參數進行一定的改進,充分利用系統的控制誤差,在每個迭代周期根據系統的誤差及控制效果,進行參數的自我調整,使系統具備更好的智能性和學習能力。為此針對上述控制方法,做出如下改進:即通過對比同一時刻,最近2個迭代周期的誤差大小以及變化趨勢對學習參數進行優化和改進。其基本思路是:通過迭代學習,如果當前誤差比之前的誤差有減小的趨勢,則表明當前系數是有效的,并且增大下一次的學習參數,使得學習的速度變快,直至誤差滿足精度要求,則停止參數學習過程。具體參數學習和改進過程如(4)式:
(4)
式中:pL為學習系數;eh為設置的學習誤差門限值,eh>0;當迭代誤差ek(t)小于誤差門限時,停止學習過程,此時引導信號rk(t)沿用前一次迭代的rk-1(t)信號;Lk(t)為第k次迭代的學習增益矩陣。
在迭代學習過程中,當系統輸出逐漸逼近期望信號的過程中,系統誤差ek(t)會越來越小,甚至可能是一個接近于0的值,因此為了防止學習參數Lk(t)突然間劇烈變化、導致系統不穩定,在學習過程中設置了誤差門限eh,只有當系統誤差超出ek(t)>eh時,系統才需要進行迭代學習。
3 收斂性分析及證明
收斂性分析的核心理念主要是依賴于壓縮映射原理[13]和不動點原理[14-15]。因為迭代學習具有重復性的特點,所以研究人員總是要求或期望系統每次都從同一初始狀態開始進行學習。初始狀態對于學習方法收斂性的證明有著重要作用,因此在大部分的收斂性證明中總是假設或設定系統的初始狀態都保持不變基[16-20],但是這一假設在實際過程中幾乎是不可能實現的。針對這一情況,本文提出的帶參數學習引導信號迭代學習方法需要在初始狀態不一致的情況下進行數學證明。
針對(4)式中提出的參數學習迭代控制方法,需要進行系統的收斂性分析和證明。根據(1)式,系統第k次迭代時的輸出yk(t)可以表示為(5)式:
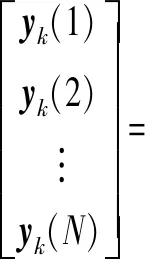
(5)
式中:xk(0)是第k次迭代時的系統初始狀態。

則系統第k次迭代時輸出和輸入之間的向量表達式(5)式可以改寫為(6)式:
yk=Guk+Dxk(0).
(6)
本文研究的空氣舵負載模擬器加載系統,在周期信號控制作用下具備一個基本特性:系統控制引導信號為連續的周期性信號時,當系統穩定后的輸出也呈現出周期性特性,該特性如圖4所示。

圖4 系統周期特性圖Fig.4 Periodic characteristics diagram
這一周期特性用數學表達式可以表示為
當rk(t)=rk-1(t)時,有
yk(t)=yk-1(t),
(7)
相應地,可以推導出如下等式:
當rk(t)=rk-1(t)時,有
uk(t)=uk-1(t).
(8)
根據系統時間上的連續性xk+1(0)=xk(N)和重復性xk+1(0)=xk(0),有
xk+1(0)=xk(0)=xk(N).
(9)
根據(1)式將xk(N)展開,可以得到如下等式:
xk(0)=ANxk(0)+Quk-1,
(10)
式中:向量Q=[AN-1B,AN-2B,AN-3B,…,AB,B],為1個參數矩陣。
(10)式就是連續性、周期性信號作用下系統狀態變量所具備的特性。在此特性基礎上,可以進一步分析系統在新提出迭代學習律下的收斂性。
系統第k+1次的誤差ek+1可以寫為如下表達式:
ek+1=yd-yk+1=yd-Guk+1-Dxk+1(0)=
rd-pG(rk+1-yk+1)-Dxk+1(0)=
yd-pG(rk+Lkek-yk+1)-Dxk+1(0)=
yd-pG(rk-yk+Lkek-yk+1+yk)-Dxk+1(0)=
yd-pG(rk-yk)-Dxk(0)-pG(Lkek+yk-yk+1)-
Dxk+1(0)+Dxk(0)=
yd-pGuk-Dxk(0)-pG(Lkek+yk-yk+1)-
Dxk+1(0)+Dxk(0)=
ek-pG(Lkek+(yd-yk+1)-(yd-yk))-
Dxk+1(0)+Dxk(0)=
ek-pG(Lkek+ek+1-ek)-D(xk+1(0)-xk(0)),
(11)
式中:ek=[ek(1),ek(2),…,ek(N)]T為系統第k次迭代時的誤差向量;Lk=[Lk(1),Lk(2),…,Lk(N)]T為系統第k次迭代時的學習增益矩陣;yd為期望信號。
由(11)式可以推導出
ek+1=ek-pG(Lkek+ek+1-ek)-
D(xk+1(0)-xk(0)).
(12)
根據(1)式,將xk(t+1)=Axk(t)+Buk(t)展開,可得
xk+1(0)=xk(N)=ANxk(0)+Quk,
(13)
根據uk(t)=p(rk(t)-yk(t)),可以推導出uk和uk-1之間的關系如下:
uk=uk-1+pLkek-1+pek-pek-1.
(14)
(13)式代入(12)式中,可得
xk+1(0)=ANxk(0)+Quk-1+pQek+
pQ(L-I)ek-1.
(15)
再根據(10)式,(14)式可以進一步化簡為
xk+1(0)=xk(0)+pQek+pQ(L-I)ek-1.
(16)
根據(15)式可以將(11)式進一步寫為如下等式:
(I+pG)ek+1=ek+[-pG(Lk-I)-pDQ]ek-
pDQ(Lk-I)ek-1,
(17)
矩陣I+pG可逆,(17)式兩端同時左乘逆矩陣(I+pG)-1可得如下表達式:
ek+1=(I+pG)-1[I-pG(Lk-I)-pDQ]ek-
p(I+pG)-1DQ(Lk-I)ek-1.
(18)
(4)式中

由此可得
(19)
|ek-1(t)|>eh,因此由(19)式可以推導出如下不等式:
即
(20)
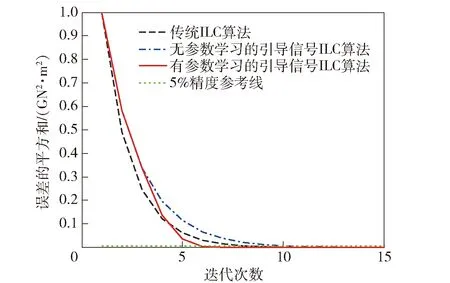
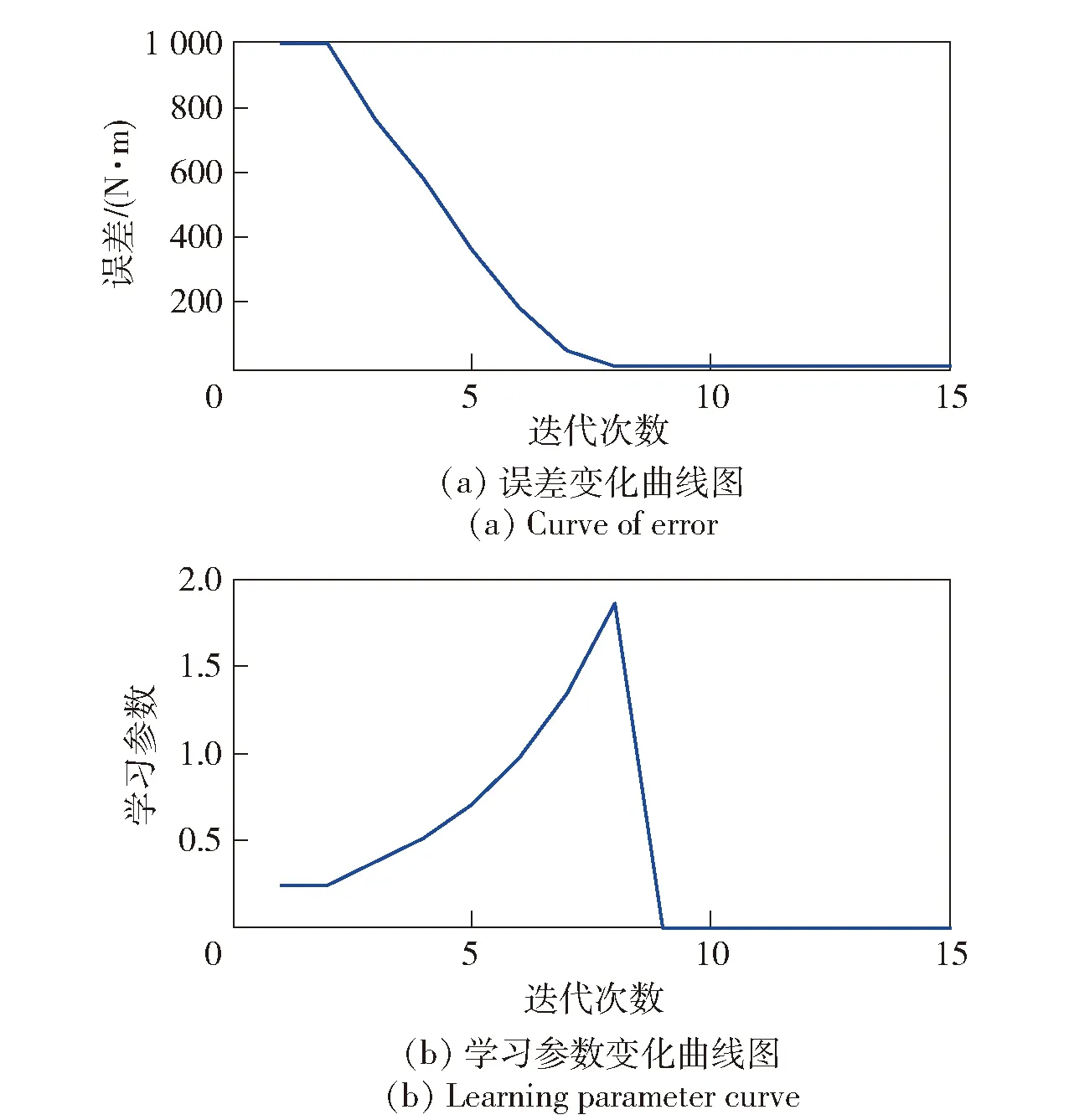
在實際系統中,系統誤差總是存在邊界的,即ek+1 (21) (21)式代入(18)式中,可得(22)式 (22) 對不等式(21)式兩邊同時取范數,并根據范數的相容性可得(23)式: (23) 為了進一步證明系統的收斂性,特引入引理1. 根據引理1,如果(23)式中滿足如下條件(24)式: (24) 至此,系統在迭代學習方法即(4)式作用下,系統的收斂性證明完畢。(24)式即系統在參數學習方法下收斂的充分條件。可以選取合適的參數L1、p、pL使得不等式(24)式成立,從而保證系統的收斂性。 為了對本文提出方法進行驗證,設計并進行了仿真對比實驗。在仿真對比實驗中,應用了傳統迭代學習方法、不帶參數學習的引導信號ILC方法和帶參數學習的引導ILC方法。引導信號在第1個迭代周期的取值為期待信號,即r1(t)=yd(t),取pL=-0.6,p=0.003. 將選定的3種方法分別用于仿真系統,針對輸入為0.5 Hz、幅值為1 000 N·m的正弦信號,系統誤差收斂情況對比如圖5所示。 圖5 收斂速度對比圖Fig.5 Comparison of convergence speeds 從圖5中可以看出,在3種控制方法作用下系統都能收斂,并使系統的控制誤差落入5%的誤差區間之內。但是從收斂速度來看,本文提出的方法具有最快的收斂速度,在第6次迭代時就使系統的控制誤差到達設定要求。而傳統ILC方法和無參數學習的引導信號ILC方法分別需要9次迭代和11次迭代。其對比結果如表1所示。 表1 收斂速度對比對表 從表1可以看出,帶有參數學習的引導信號ILC具有更快的收斂速度和更好的控制效果。 針對參數學習過程中的某一時刻,以t=500 ms時刻為例,其前15次迭代過程中該時刻點的學習參數Lk(500)的變化曲線如圖6所示。 圖6 學習參數變化曲線圖Fig.6 Changing curve of learning parameter 從圖6中可以看出,在迭代過程中,該時刻點的誤差呈現減小的趨勢,表明該點當前的參數調整是有效的,因此學習參數一直呈現增長趨勢,期望該點的控制誤差能夠盡快減小到門限值。當該點誤差在第6次迭代達到設定的門限值以后,該點停止迭代學習,學習參數變為0并維持不變。 1)針對傳統迭代學習在實際控制系統中出現的系統發散問題,本文提出了帶參數學習的引導信號ILC方法。該方法充分結合了PID控制和迭代控制的優點,使系統在完全受控的情況進行迭代學習,并讓系統具備了一定的智能型。為了增強系統的智能型,提出的改進方法使得系統的學習參數本身也具備學習能力。 2)在收斂性分析和證明中,針對實際情況中每個迭代周期初始狀態不一致的情況,本文證明了帶參數學習的引導信號ILC方法的收斂性并給出了收斂的充分條件,說明了該方法的實用性。 3)將改進后的的控制方法同傳統ILC方法和不帶參數學習的引導信號ILC方法進行對比,從實驗對比結果可以看出,改進后的控制方法具備更快的收斂速度和更好的控制效果,充分說明了本文方法的有效性和優越性。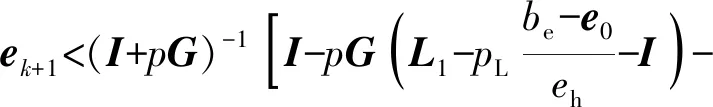
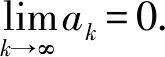
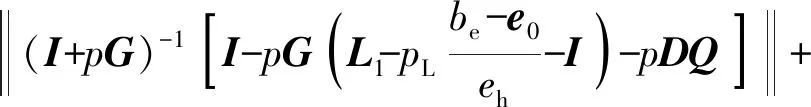
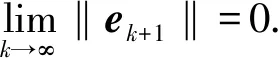
4 對比實驗及驗證

4 結論

