基于改進遺傳算法優化BP神經網絡的銷售預測模型①

圣文順,趙翰馳,孫艷文

1(南京工業大學浦江學院,南京 211200)

2(河海大學 計算機與信息學院,南京 210008)

隨著經濟環境的高速發展,眾多企業步入科學化管理時代,但企業管理人員對企業的銷售預測管理方面仍有疏漏,甚至出現了各種問題.比如管理人員常用的銷售預測模型為專家法,就是靠有經驗者的從事經驗來對銷售進行人為主觀預測,與本文提出的改進BP神經網絡算法相比有這快速、簡單的優點.但同時也有不可彌補的缺點,每位專家的預測可能不一樣,帶有嚴重的差異性與客觀上的不可靠性.還有時間序列方法中最為簡單的指數平滑法[1],通過不同的權重來控制預測的精度,但是隨著預測時間的延長精確率會大打折扣.再者如ARIMA模型,相對于前兩者就較為復雜,其原理是利用歷史銷量對未來銷量進行預測,但是ARIMA模型的建立,需要數據集具有趨勢性強的特點,對于趨勢性弱的數據集,則通過ARIMA模型得到的結果預測效果也不理想.

作者就以上3種預測方法的優缺點,提出進行改進優化后的BP神經網絡算法預測模型,同時利用指數平滑法和遺傳算法模型得到的結果與改進后的BP神經網絡算法進行對比實驗,以驗證其在準確度、對數據集趨勢性依賴強度、預測時間長度失準度方面的優化提升.

1 優化BP神經網絡的算法設計基礎

1.1 時間序列模型

時間序列,是一組按時間順序排列并隨時間的變化而變化的數據序列[2].一個時間序列往往是由上兩點或多點以變化的方式疊加或耦合起來的.

所選擇的二次指數平滑法[3]處理數據可預防實際在時間序列出現直線形式的上下波動時產生的“滯后”現象[4],并能自動識別數據模式的變化,加以調整.

1.2 BP神經網絡

BP神經網絡是帶有隱含層的多層前饋網絡,是一種誤差反向傳播算法[5].此算法由信息正向傳遞和誤差反向傳播組成,其基本原理是不停地修正網絡中各層節點的權值、閾值,直到網絡輸出達到目標輸出值,且具有很好的泛化能力.

2 優化BP神經網絡的具體算法設計

2.1 算法原理

可泛化型時間序列校正下的遺傳算法優化BP神經網絡預測模型(簡稱TC_GA_BP神經網絡預測模型),使用了合并傳統BP神經網絡以及遺傳算法[6-8]對BP神經網絡進行改進,利用時間序列預測值和改進后的GA_BP神經網絡[9-11]進行“誤差值”比較,利用時間序列模型預測結果誤差呈增函數關系的特點,使用其與GA_BP神經網絡的差值進行一元線性回歸[12,13],討論出兩者之間誤差值的函數擬合關系,再利用擬合函數[14]進行誤差測算,最后通過兩者誤差規律,校正其中一者的預測值,這里選擇對GA_BP神經網絡的預測值進行校正,從而最后得到校正后的預測值.

已知BP神經網絡算法的收斂速度較慢是由于BP神經網絡算法究其本質是梯度下降法,因為需要優化的目標函數非常復雜,所以出現“鋸齒形現象”在所難免,這會使得BP算法低效.與此同時正也因為目標函數的復雜,BP網絡的神經元輸出在接近0或1的情況下,會出現一些平坦區,在這些平坦區內,權值誤差變化很小,使訓練過程幾乎停滯.再者為了使網絡執行BP算法,必須預先賦予網絡的步長更新規則,這樣也會使得算法低效.就此引發出利用遺傳算法優化BP神經網絡的優化方式.

而在面臨小數據量的處理情況時,由每個個體獨立討論是有可能利用線性關系處理非線性問題,真實值與預測值之間一定會存在誤差.故令距離為d,那么就有dtr為時間序列預測與真實值之間的誤差,dnr為改進后BP神經網絡與真實值之間的誤差,會出現數值大小關系上不同的6種情況.

為解決此問題,對時間與真實值之間的誤差dtr和改進后BP神經網絡與真實值之間的誤差dnr進行一次減法運算,距離令為dtn,對dtn與試驗次數之間進行一元線性回歸,線性回歸的函數關系結果,視為自校正函數的核心部分,得到的一元回歸模型忽略隨機擾動項并記總體回歸系數為 α.

得到了一元回歸模型的具體表達,利用時間序列預測值減去回歸模型得出的對應誤差量,得出修正E值,即可以用來的再次優化GA_BP神經網絡的傳遞權值和各個神經元的閾值,以達到利用校正函數[15]修正GA_BP神經網絡的目的.

在GA_BP神經網絡的優化后,依舊存在步長 η的選擇問題,過大的 η會導致收斂過快引起不穩定,過小的 η雖然避免了不穩定,但是收斂速度就會很慢.此時針對于利用增加優化因子 α的方法再對GA_BP算法進行二次優化,利用該動量有效的改變 η的值,使得 η不再是一個恒定的值,引入這個優化因子之后,使得調節向著底部的平均方向變化,不至于產生大的擺動,即優化因子起到緩沖平滑的作用.若系統進入誤差函數面的平坦區,那么誤差將變化很小,于是 Δw(t+1)近似于Δw(t),而平均的 Δw將變為:其中系數變得更為有效,使調節盡快脫離飽和區,具體在算法中加入“優化因子”的關系式,見式(1)：

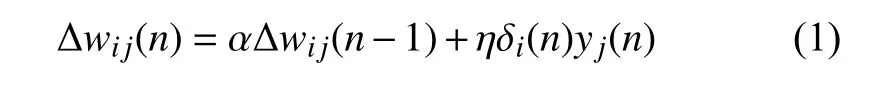
其中,第二項是傳統BP神經網絡的修正量,第一項就是上文提及的優化因子,α為某一個正數優化因子具體所起作用就是：當順序加入訓練樣本時,上式可寫成以t為變量的時間序列,t取0到n,因此,上式可看做是Δwij的一階差分方程,對Δwij(n)求解,見式(2)：

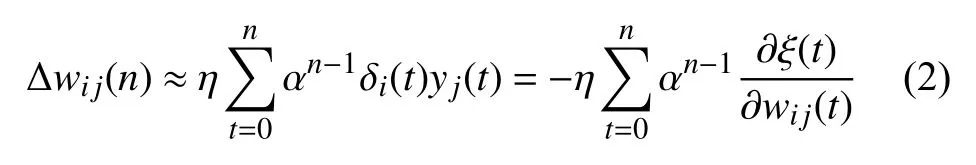
結合上面分析結果,二次改進后wij=wij-ηdjOi的簡單形式,見式(3)：

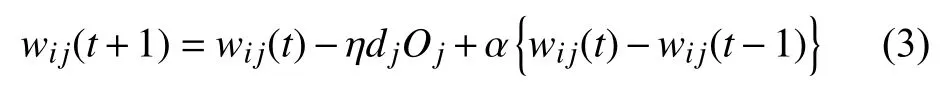
其中,O為各層元素的實際輸出值.

經過對GA_BP神經網絡預測值修正后,可以得到誤差平方和Ec,及E的修正值.利用數學方法,對GA_BP神經網絡的權值與閾值進行再一次帶有優化因子的優化,步驟如下：

已知輸出層的輸出誤差Ec,見式(4)：

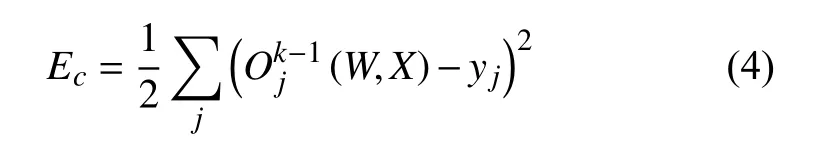
其中,W為權矢量,X為輸入矢量,yj為期望輸出.展開至隱層誤差Ec,見式(5)：

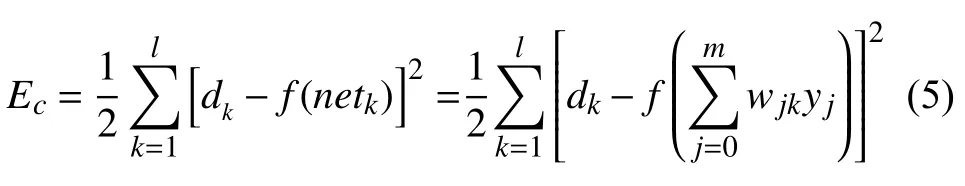
最后推導至輸入層Ec,見式(6)：

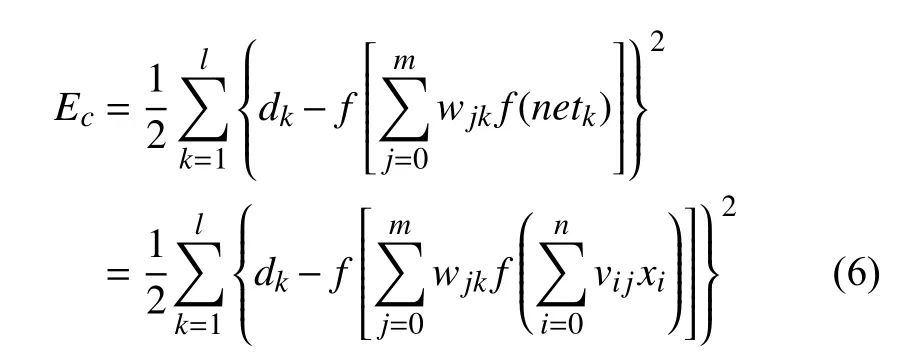
根據誤差就可以得出權值函數wc和vc.最后成功通過再一次的權值和閾值調整來更新校正函數,修正GA_BP神經網絡,得到TC_GA_BP神經網絡.

2.2 算法構建

基于優化BP神經網絡的流程圖如圖1所示.

圖1 基于優化BP神經網絡的流程圖

3 優化BP神經網絡在Kaggle競賽數據集中的應用

利用上文提到的算法對Kaggle競賽數據集[16]進行銷售預測.

3.1 時間序列仿真實驗

使用由Kaggle競賽提供的Restaurant Revenue Prediction數據集,抽取其中的一家名為“Stanbul”的餐廳作為實驗對象進行仿真實驗.利用已有銷售額統計的50條數據,使用時間序列預測模型的二次指數平滑法對其進行時間序列仿真預測,而且與一次指數平滑法的結果做對比仿真結果如圖2、圖3.

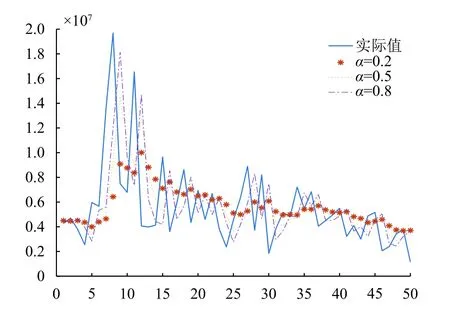
圖2 一次平滑指數預測圖

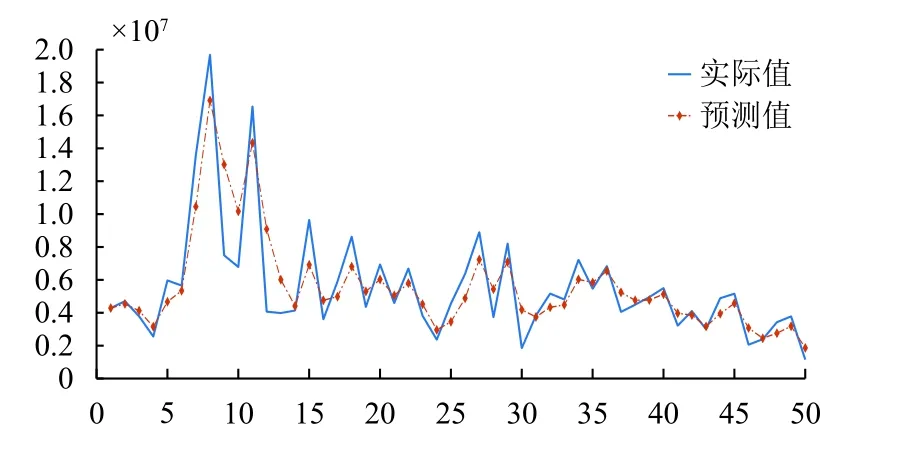
圖3 二次平滑指數預測圖

經過試驗,實驗結果與理論預測完全符合,一次指數平滑法在25個數據集仿真結果中,出現了大量的滯后反應,無論α=0.2,α=0.5還是α=0.8都無法改變滯后反映,這也正體現了二次指數平滑預測較高的準確度(誤差率25.7471%),為下文提供了可行方案.

3.2 算法實現過程

將優化后的 BP 神經網絡算法,與經典 BP 神經網絡、時間序列模型、遺傳算法改進神經網絡進行銷售預測的比較.在已有銷售額統計的50條數據中,抽取其中的25條作為仿真訓練集,剩余的25條作為仿真驗證集,用于驗證誤差.3種算法的誤差對比分析如圖4、圖5和圖6所示.

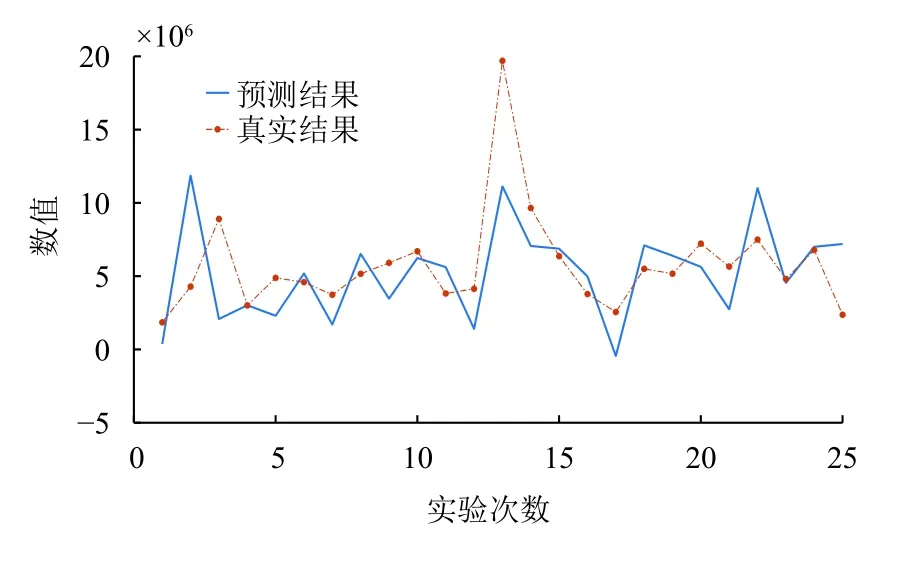
圖4 傳統BP神經網絡預測圖(誤差為50.2401%)

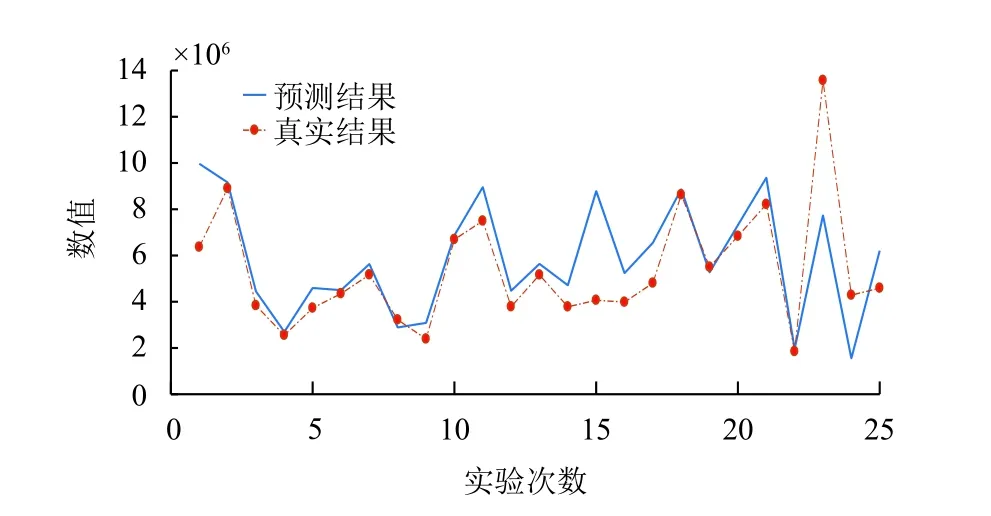
圖5 遺傳算法BP神經網絡預測圖(誤差為23.629%)

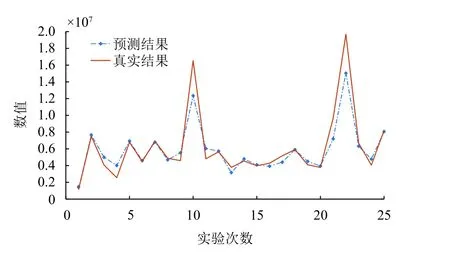
圖6 TC_GA_BP神經網絡預測圖(誤差為12.088%)

由圖像直觀看出,在相應的被修正點上,預測值比遺傳算法改進BP神經網絡的結果預測值更為接近真實值結果,而誤差率也降至約12%,提高近11%.由此可知,新提出的TC_GA_BP神經網絡模型的預測輸出結果,在預測的準確度上大大改善,比另外3種模型的預測更加接近未來真實值.

3.3 結果分析

部分預測結果如表1所示.

表1 預測結果對比

統計數據表明,TC_GA_BP神經網絡預測模型的仿真效果最好,達到12.088%；而傳統BP神經網絡的結果誤差最大,達到50.2401%,被認為是不可信的預測模型；時間序列預測模型和改進后的BP神經網絡都有良好的仿真實驗,但仍沒達到TC_GA_BP神經網絡的預測精度.因此TC_GA_BP神經網絡在同屬性的數據集預測上優于其他3種預測模型.

4 總結與展望

文章首先采用時間序列模型減少源數據的誤差,利用優化后的BP 神經網絡,建立起適當的銷售預測模型,并具體應用于某數據集中.實驗表明優化后的 BP神經網絡算法在提高了預測準確度和收斂速度的同時,也簡化了網絡結構,減少了數據的誤差.由于可利用于訓練網絡的數據量太少,導致網絡訓練情況不佳,達到的準確度不是太高.如需進一步的深入研究,可考慮在現有算法基礎上訓練更多的數據集.