基于改進的支持向量機決策樹電梯載重分類方法研究

（華中科技大學無錫研究院，江蘇 無錫 214100）

SVM是機器學習中經典分類器之一，常被用于解決低維數據線性不可分問題，通過核函數將低維數據映射到高維空間，因此在模式識別、小樣本等問題中，SVM有著不可比擬的優勢。然而，SVM本身是一個二類分類器，對于多類分類問題，可以通過兩種方法進行問題推廣：①通過二次優化來描述整個問題；②將一個問題分成多個問題，如：1-a-1、1-a-r、DAGSVM以及SVMDT。

張先武等人分別詳細闡述了1-a-1、1-a-r、DAGSVM的基本思路：1-a-1是通過投票方法決策，在票數相同的情況下，存在不可分區域；1-a-r將N類問題分成N個分類器，在分類過程，分類速度較快，但每次構造分類器都要將整個工作集作為訓練樣本，訓練速度會變慢；DAGSVM是在1-a-1的基礎上提出來的，在分類階段只需要使用N-1個分類器，分類速度比1-a-1和1-a-r都要快，但該方法的泛化能力與有向無環圖中的位置有關。Kumar和Jair Cervantes等人在傳統SVM的基礎上，提出使用DT算法在SVM決策邊界上劃分3個類節點，通過使用參數來確定數據屬于哪類。Anish Jindal等人將SVMDT方法引入到工業能源分類問題中，準確率有了很大提高。然而引入來搭建樹結構時存在一個問題，當樹根節點出現分類誤差時，誤差會隨著樹的層數的增加而積累越多，最終分類結果與實際結果之間相差甚遠。王道明和Shih-Wei Lin等人在此基礎上提出了基于自變異粒子群（PSO）聚類的決策樹SVM的算法，在每個SVM訓練前針對每個子節點通過PSO聚類算法進行二分類劃分，確定各子分類器的位置以及訓練樣本，該方法以增加訓練樣本時間來換取優良的分類性能。

雖然通過引入粒子群算法優化樹結構，但仍然存在缺陷，PSO算法容易陷入局部最優。基于此本文引入模擬退火算法，既保障粒子群算法的全局尋優能力，也避免了粒子群算法易陷入局部最優，使得模型的訓練效果達到最優。

1 支持向量機決策樹

1．1 支持向量機

SVM是機器學習中較為常見的方法之一，被廣泛應用于分類和回歸問題，它的核心思想就是在正、負樣本之間尋找最優分類超平面。

假設訓練集樣本為(xi, yi)，xi為第i 個樣本數據，i = 1,2,...,I ，I為樣本數，xi∈Rq(R為實數域，q為輸入數據的維度)；yi為第i 個樣本數據的類標簽，yi∈{- 1 ,+1}。

當樣本集線性不可分類時，引入松弛變量ξi(ξi>0)，i = 1,2,...,I ，利用式(1)和(2)求解最優分類面。

其約束條件為：

式中：C為懲罰因子，表示目標函數的損失情況；C越大，損失越大。

在以上基礎上引入Lagrange函數L(w,b,a)為：

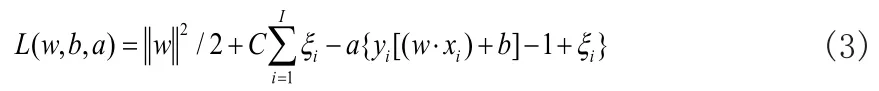
式中：a為Lagrange因子。

在低維空間，樣本無法進行線性分類時，SVM通過核函數K(xi, xj)將樣本數據xi從低維空間映射到高維空間進行線性分類，根據Mercer條件得到最優決策函數F(xi)：

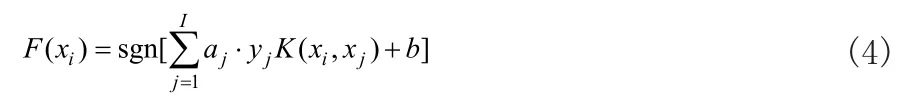
式中：aj表示a的其中第j個解。

在本文中，選取高斯核函數K(xi, xj)為：

式中：σ為寬度參數，控制取值范圍。

1．2 支持向量機決策樹

SVMDT的核心思想是將多分類問題分解為多個二分類問題，通過比較不同類之間的歐氏距離進行分類，距離越大越容易分。將整個樣本集有選擇的分為正樣本集和負樣本集，分別記為C1和C2，N1和N2分別為C1和C2的類別個數；N=N1+N2為所有節點需要劃分的總類別數；Zn表示第n類樣本，n= 1,2,...,N；Zn的樣本數為ln。分類器的建立過程如下：

（1）利用式(6)計算出N個類中每個類的樣本中心An為：

式中：zu為Zn中第u個樣本向量。

（2）同樣計算出正、負樣本集C1和C2的中心e1和e2，并利用式(7)計算C1、C2之間的歐氏距離為：

（3）利用式(8)計算正樣本集中每個類的樣本中心到正樣本集中心e1的平均距離為，負樣本集中每個類的樣本中心到負樣本集中心e2的平均距離為，如下式：

式中：Zn∈C1表示Zn是正樣本集中的樣本，則利用式(8)上式計算；否則利用式(8)下式計算。

（4）利用式(9)計算最大距離值d，以此來劃分出類：

（5）重復上面2到4步，知道所有的類分出來為止。

2 粒子群優化的支持向量機決策樹

SVMDT雖然縮短了訓練和分類的時間，提高了分類精度，但在構建樹結構時，若根節點出現分類錯誤，會順著子節點的延續而往下積累，最終導致與實際結果相差很大。基于此，通過引入PSO聚類算法來優化樹結構，可將數據集進行最優劃分。

2．1 PSO 算法

PSO源于鳥群捕食行為的研究，核心思想是通過群體中個體之間的協作和信息共享來尋找最優解。PSO算法需要預設類簇個數，每個粒子代表各類簇的類中心，粒子Xi以及速度Vi如下:

式中：Cij表示第i個粒子所代表的第j個類中心。Vij表示第i個粒子第j類的速度。PSO算法具體流程如下：

（1）設定進化次數以及種群規模，初始粒子和速度。

（2）根據粒子適應度函數f計算每個粒子的適應度值，更新個體極值，如式(11)；

式中：je為類內離散度之和，N為類的個數，Pm屬于Cij所在的類。

（3）尋找全局極值和全局極值位置。

（4）根據式(12)和式(13)更新粒子的位置及速度。

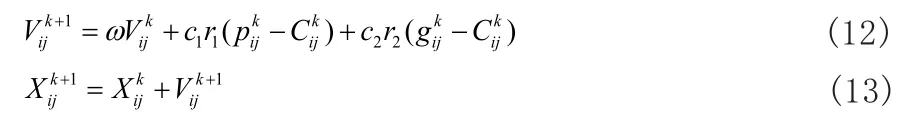
（5）若達到結束條件，則輸出最優解位置；否則返回2。

2．2 PSO-SVMDT 算法

通過PSO將訓練樣本進行二分類，生成最優決策樹以實現最大樣本分離。基于PSO的SVMDT具體生成步驟如下：

Step1：將整個訓練樣本作為初始根節點，利用PSO算法將初始根節點劃分為兩類，形成兩個子類點。

Step2：判斷子節點是都包含一個類，若是轉向Step4，否則跳至Step3。

Step3：調用PSO算法再將節點劃分為兩個子節點，跳回Step2。

Step4：節點為葉子節點，算法結束。

3 基于模擬退火的粒子群優化的支持向量機決策樹

3．1 模擬退火算法的原理

模擬退火算法(Simulated Annealing，SA)最早的思想是由N. Metropolis等人于1953年提出。1983年,S.Kirkpatrick等人成功地將退火思想引入組合優化領域。它是基于蒙特卡洛迭代求解策略的一種隨機尋優算法[10]。具體算法如下：

Step1：初始化參數，如Metropolis步長因子、初始溫度、終止溫度、Boltzmann常數。

Step2：在當前解Xi和新的解Xi+1可接受度(P)定義如下：

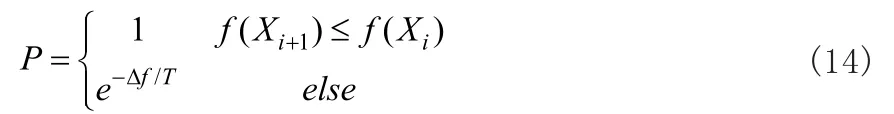
式中：f表示目標方程。Δf=f(Xi+1) -f(Xi)；T是溫度。依照min(P) >R[0,1]，則接受Xi+1。其中R[0,1]表示0到1之間的隨機數。

式中：C表示0到1之間的衰減因子。如果滿足收斂條件，則算法結束，否則返回Step2。

由于有退火溫度T控制著最優值的優化問題，并且同時以e-Δf/T來接受解。

3．2 基于模擬退火的粒子群優化算法

算法的具體步驟如圖1所示。

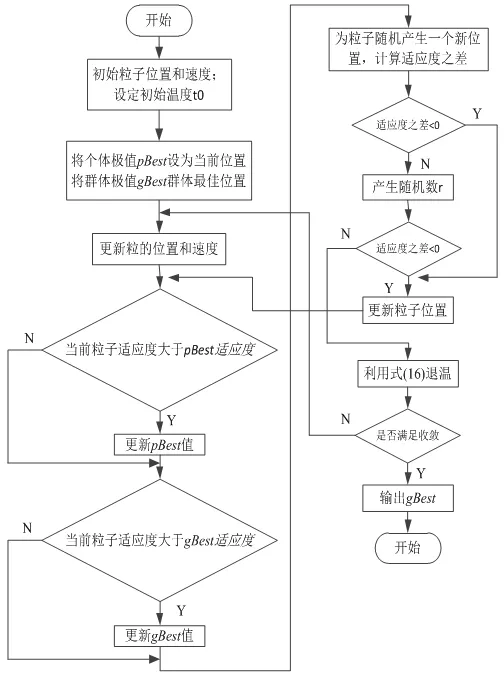
圖1 SA-PSO算法流程圖

4 實驗驗證與分析

4．1 實驗數據選擇

本文實驗所用數據參數包括：時間、速度、電壓、電流、頻率以及當前樓層，由于電梯中使用變頻控制，并且每臺電梯在出廠后，運行速度曲線都是預設好的，而當前樓層只是顯示電梯轎廂的位置，因此，通過可視化已有數據后發現不同載重下的電壓不相同，如圖2所示。

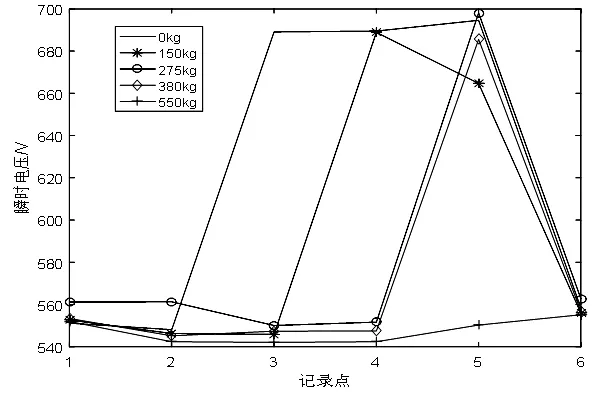
圖2 不同載重時上升過程電壓變化曲線

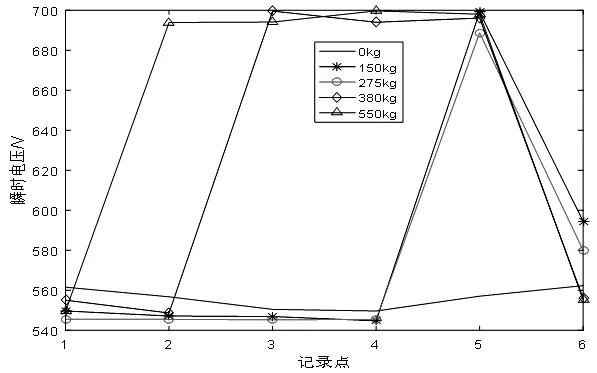
圖3 不同載重時下降過程電壓變化曲線

圖2和圖3中，共五種載重情況，0kg對應電梯空載情況，150kg對應電梯25%額定載重情況，275kg對應電梯50%額定載重情況（半載），380kg對應于電梯75%載重情況，550kg對應滿載情況。

顯然，不同載重情況可以通過變化曲線反映出來，因此可以通過分離不同電壓變化情況來區分不同載重情況。選取處理好并已知載重情況的數據對本文所提出的改進分類算法進行驗證。

4．2 實驗仿真

本次仿真是在matlab軟件下進行，電腦內存6G，CPU2.10GHz，操作系統Win10。測試樣本中載重情況共五類：空載、輕載、半載、重載以及滿載。本文通過對比基于粒子群算法(PSO)、模擬退火算法(SA)、遺傳算法(GA)的分類精度，來驗證本文所提方法在所測數據集中的分類效果。

本文所選用SVM核函數為高斯核函數，參數C=100，σ=10。PSO算法的c1=c2=1.5，粒子群的規模為20，迭代次數為300，SA初始溫度設為900℃，終止溫度設為0.001℃，衰減因子為0.85。將SA-PSO與GA、SA和PSO優化算法進行對比，結果如圖4所示。

從圖中可以發現，SA-PSO優化后的算法不僅收斂速度比其它三種優化算法的快，而且迭代次數也是四種算法中最少的，分類精度也高于其他算法，SA-PSO的收斂性能更好。實驗結果如表1所示。

圖4 PSO與SA-PSO的分類精度比較圖

表1 不同改進算法分類結果比較

由于在實際電梯運行過程中，空載運行次數相比于其他四種載重情況的運行次數要多，因此，實驗中以空載情況的分類正確率作為整個算法的分類精度。在表中可以發現，基于GA算法的分類精度比PSO優化算法要高，但訓練時間比較長，基于SA算法的訓練時間雖然最短，但分類精度較低。本文所提算法所耗時間較短，相比SA和PSO優化算法，分類精度有了較大的提高，這也證明了本文所提改進算法的可行性。

5 結語

本文基于粒子群算法尋找全局最優能力強以及易陷入局部最優的缺陷，提出了一種基于模擬退火的粒子群優化算法，相比一些傳統的優化算法，在分類精度上有了一定的提高。