節點局部Fiedler向量中心性差值社區發現算法*

鳳麗洲，覃 悅，楊貴軍

天津財經大學 統計學院，天津 300222

1 引言

現實世界中的大部分系統都能以網絡的形式表示，如人際關系網、信息傳播網、神經元網、蛋白質交互網等。這些網絡往往具有很高的復雜性，被稱為復雜網絡。與隨機網絡不同，復雜網絡普遍具有“同一社區內節點聯系緊密，不同社區間節點聯系稀疏”的特性，這一特性被稱為社區結構[1]。復雜網絡中的社區結構研究主要針對兩個重要問題展開：（1）如何識別復雜網絡中的社區結構，即社區發現；（2）如何識別連接不同社區的關鍵節點，即關鍵節點發掘。這兩個問題的研究對于解決謠言傳播、電網保護、抑制傳染病擴散等現實問題具有重要的理論意義和廣泛的應用前景。

2 相關工作

Girvan與Newman[1]最早于2002年提出了社區發現的概念。此后，圍繞著社區發現問題，各領域學者們提出了大量有效的社區發現算法。這些算法大致可分為4類：

（1）基于模塊度優化的社區發現算法，根據優化算法的思想，將一種用于度量社區發現結果優劣的指標——模塊度[2-3]（modularity）作為目標函數，旨在尋找一種使得模塊度最大的社區劃分方案，如快速Newman（fast Newman）算法[4]、魯汶（Louvain）算法[5]、模擬退火（simulated annealing）算法[6]等。文獻[7]在魯汶算法的基礎上加入了孤立節點分離策略，縮短了算法的運行時間；文獻[8]針對網絡變化對靜態算法影響較大的問題，提出一種基于模塊度的增量學習算法，保持了社區發現的實時性；文獻[9]基于層次聚類的思想，利用拓撲勢迭代地擴展社區，最終從各層的社區劃分中選擇一個模塊度最大的作為劃分結果。

（2）基于啟發式規則的標簽傳播（lable propagation algorithm）算法[10-12]將社區劃分視為節點標簽預測問題，文獻[13]針對標簽傳播算法存在的不必要更新問題，引入節點信息列表，提高了算法準確率；文獻[14]基于度中心性設計了節點參與系數，解決了標簽傳播算法在節點更新時順序的不確定性對社區發現結果的影響問題。

（3）基于動力學與仿生模擬的社區發現算法，如基于Markov動力學理論的Markov聚類算法[15]、基于自旋模型的社區發現算法[16]、蟻群算法[17]和遺傳算法[18]，文獻[19]設計了一種節點對社區的隸屬度計算方案，并將其與遺傳算法結合，提出一種能夠作用于大規模重疊網絡的改進遺傳算法。

（4）以圖論作為理論支撐的聚類算法，如譜聚類（spectral clustering）算法[20]和基于節點中心性的社區發現算法[1，21]。其中基于節點中心性的社區發現算法是一種可同時進行關鍵節點發掘與社區發現的算法，其準確率與速度取決于中心性度量指標的選擇。根據計算方式的不同，中心性度量指標可分為兩類：①全局中心性，如介數中心性[1]（betweenness centrality）、緊密度中心性[22]（closeness centrality）、特征向量中心性[23]（eigenvector centrality）等。文獻[1]提出一種基于介數中心性的圖分割社區發現算法（Girvan and Newman algorithm，GN）；文獻[24]提出了一種基于社區動態網絡節點介數中心性的更新算法，提高了介數中心性的計算效率，并將其運用到CNM（Clauset，Newman and Moore algorithm）等社區發現算法中。全局中心性的計算需要預先獲知圖的全局拓撲結構信息，這使得基于全局中心性的社區發現算法往往具有較高的準確率。但由于其復雜度較高，對于大型網絡的計算是不可行的。②局部中心性，如度中心性[23]（degree centrality）、節點質量[25]（node mass）等。文獻[26]將節點的度中心性作為該節點的關鍵性度量指標，提出一種基于核心節點擴展的社區挖掘算法（community mining algorithm based on core nodes expansion，CNE）；文獻[27]將網絡轉化為邊圖，基于節點的度中心性，迭代地將邊圖中的節點加入到已有社區中。度中心性雖然計算較為簡便，但只能反映出節點的局部特征，忽略了節點對于全局的影響，這會影響社區發現與關鍵節點發掘的結果。

為了解決上述節點中心性存在的缺陷，Chen 和Alfred[28]提出一種局部中心性度量指標——局部Fiedler向量中心性（local Fiedler vector centrality，LFVC），并提出了一種基于LFVC的貪心社區發現算法（greedy community detection algorithm by node-LFVC，GCDN）。然而，GCDN算法在關鍵節點與關鍵邊的識別過程中經常出現錯誤識別問題，即將一些非關鍵節點誤識別為關鍵節點，導致錯誤信息傳遞，給后續社區劃分帶來負面影響，降低社區劃分的準確率。在圖分割的過程中易劃分出大量的孤立節點，破壞網絡信息完整性，導致部分社區結構信息的損失。

本文深入分析了網絡拓撲結構對節點LFVC 值的影響，提出一種節點LFVC 差值社區發現算法（community detection algorithm with difference of node-LFVC，CDDN）。該算法主要考慮了以下兩條信息：（1）聯系不同社區間的關鍵節點與關鍵邊存在著的必然鄰接關系；（2）關鍵節點的鄰邊并非都是關鍵邊。CDDN 算法在圖分割過程中綜合利用這兩條信息，設計了一種僅移除LFVC最大節點的部分關鍵鄰邊的邊移除規則，可以有效解決GCDN 算法僅考慮節點LFVC、忽略邊的LFVC 所造成的關鍵節點錯誤識別問題。此外，由于本文算法僅移除該節點部分關鍵鄰邊，可以規避GCDN 算法在圖分割時不加區別地刪除LFVC 最大的前q個節點的全部鄰邊所產生的大量孤立節點現象。

在真實網絡上的對比實驗結果表明，與已有算法相比，改進算法在各規模的網絡上均保證了較好的時間效率，同時具有較高的準確性，性能明顯優于已有算法。

3 基于LFVC的社區發現算法

3.1 局部Fiedler向量中心性

令G=(V,E)表示一個復雜網絡構成的無向無權圖，其中V、E分別表示節點集合與邊集合。具有n個節點的圖G可由其鄰接矩陣An×n表示，其中：

令

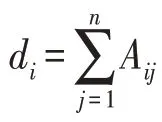
表示節點i的度，Dn×n為G的度矩陣，其中：

矩陣L=D-A稱為G的Laplace 矩陣，L是半正定矩陣，有[29]：

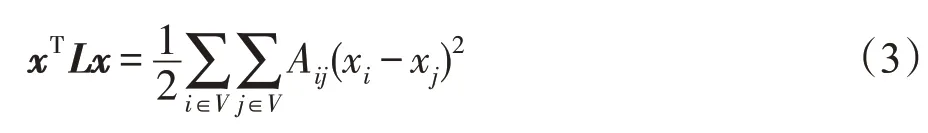
令λi(L)表示L的第i小特征值，其中λ1(L)=0。λ2(L)則有如下兩個定義：

定義1（代數連通度）λ2(L) 稱為G的代數連通度。

定義2（Fiedler向量與Fiedler值）λ2(L)對應的特征向量稱為G的Fiedler向量，其第i個分量稱為對應節點的Fiedler值。

令G′表示從圖G中移除一條邊(i,j)所得到的新圖，G的Laplace矩陣增量表示為ΔL=ΔD-ΔA，其中ΔD和ΔA分別表示度矩陣D的增量和鄰接矩陣A的增量。G′的Laplace矩陣表示為。令ei表示第i個元素為1，其余元素全為0的n維常向量，則G′的Laplace矩陣為：

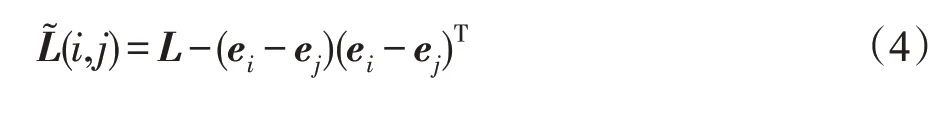
根據Courant-Fischer定理，任意連接圖的代數連通度可表示為：

令y表示L的Fiedler向量，則根據式（3）～式（5）有：

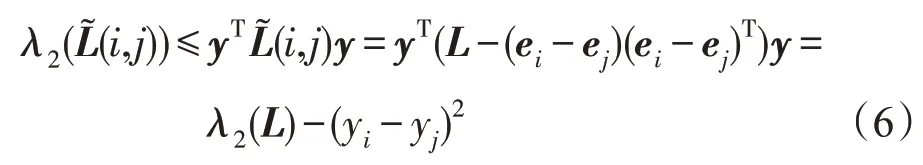
基于上述理論，將LFVC定義如下：

定義3（邊LFVC）設(i,j)為圖G=(V,E)中的一條邊，即(i,j)∈E，y為G的Fiedler 向量，yi表示節點i在y中對應的分量，則邊(i,j)的LFVC為：

定義4（節點LFVC）設i為圖G=(V,E)中的一個節點，即i∈V，Ni表示i的鄰接節點集，y為G的Fiedler向量，yi表示i在y中對應的分量，則節點i的LFVC為：

為了避免概念混淆，本文將連接著兩個社區的邊定義為關鍵邊，將負責與不同社區進行聯系的節點定義為關鍵節點。

3.2 基于LFVC的貪心社區發現算法

Chen 和Alfred[28]在2015年提出基于LFVC 的貪心社區發現算法（GCDN）。該算法的核心思想是依次移除LFVC最大的節點及其全部鄰邊，使圖G的代數連通度以最快速度減小。GCDN 算法分為兩步：（1）找到當前圖的最大連通子圖，計算其中每個節點的LFVC 值，給定常數q，依次刪除LFVC 值最大的q個節點及其鄰邊，將該q個節點認定為關鍵節點，記為集合R；（2）將R中的所有節點加入到它們相應鄰接節點最多的社區。

3.3 基于LFVC的貪心社區發現算法問題分析

GCDN 算法存在兩個問題：（1）會將一些非關鍵節點與邊錯誤地識別為關鍵節點與關鍵邊；（2）會產生大量的孤立節點，且并未對這些孤立節點進行處理。這兩個問題會降低社區發現算法的準確性，破壞網絡的信息完整性，造成社區結構信息的損失。

如圖1所示的網絡由{1，2，3，4，5，6}、{7，8，9，10，11}、{12，13，14，15，16}3個社區構成。其中，{1，2，5，7，8，12，13}是7個聯系不同社區的關鍵節點，稱為邊緣節點（margin nodes）。節點6和11的度為1，稱為懸掛節點（dangling node），連接懸掛節點的邊稱為懸掛邊（dangling edge）。為了將該網絡劃分為3個不相連的社區，最合理的策略是移除連接3個社區的6條關鍵邊{(1，8)，(1，12)，(2，13)，(5，7)，(7，13)，(8，12)}。

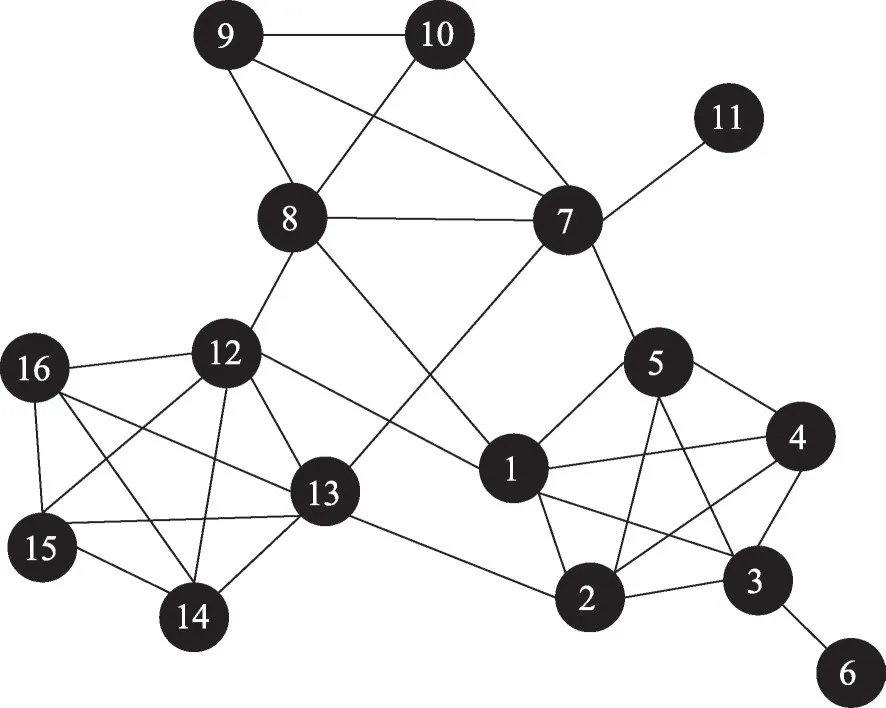
Fig.1 Network of 3 communities圖1 由3個社區構成的示例網絡

表1為圖1網絡中各節點的Fiedler值。由定義3和定義4可知，節點的LFVC值與其自身及其鄰接節點的Fiedler 值有關。社區中的節點越接近邊緣節點，其Fiedler值的絕對值越小[30]。若一個節點的鄰點集包含懸掛節點，則該節點Fiedler 值的絕對值大于同級別節點。因此，懸掛邊、懸掛節點及其鄰點往往具有較高的LFVC 值。由表1可知，LFVC 最大的節點和邊分別為節點3和邊（3，6）。

采用GCDN 算法移除LFVC 最大的1個節點后所得社區劃分結果如圖2所示，其中紅色節點表示算法識別出的關鍵節點，綠色節點和黑色節點分別代表劃分后獲得的兩個社區。顯然，這樣的社區劃分結果并不合理。

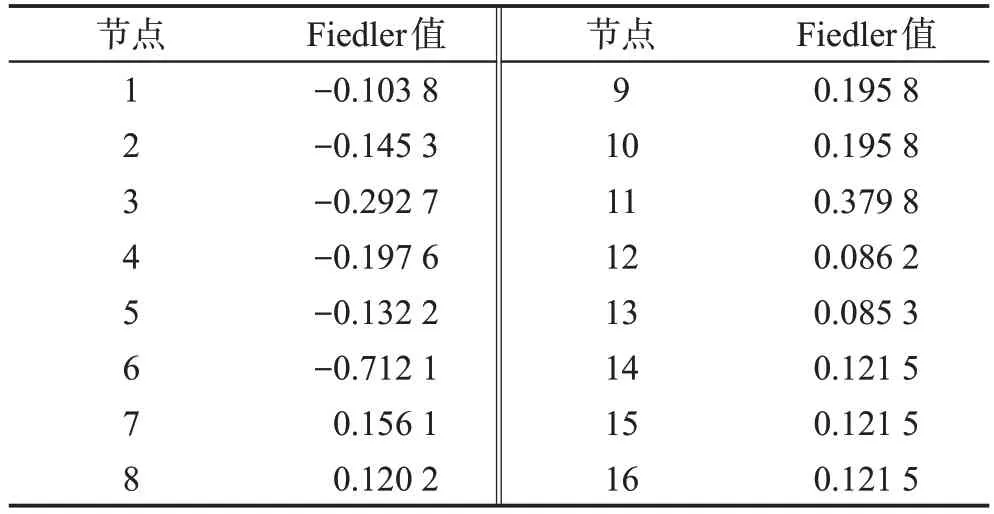
Table 1 Fiedler values of network depicted in Fig.1表1 圖1中各節點對應的Fiedler值

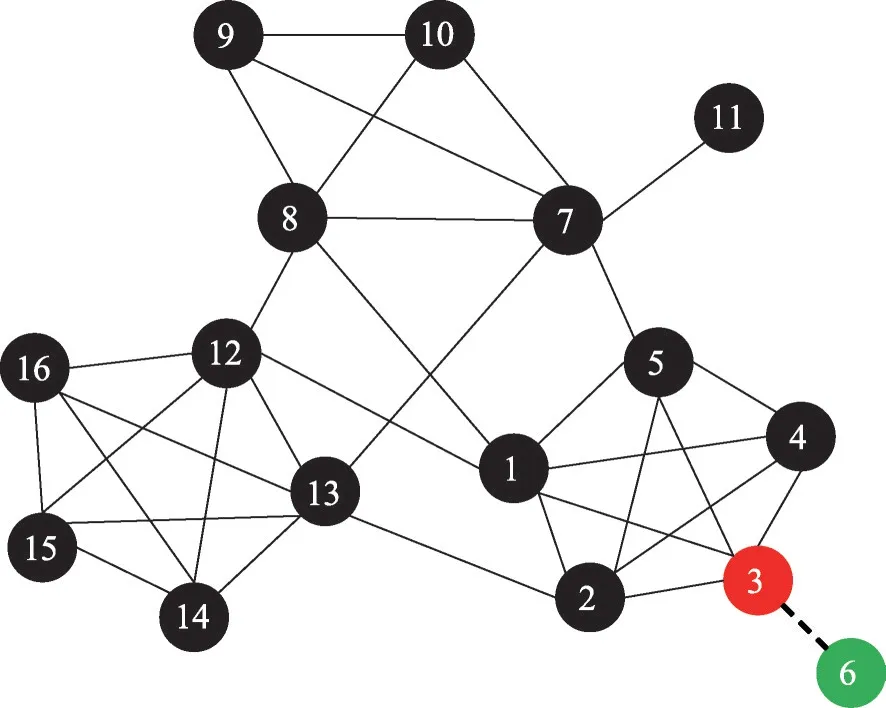
Fig.2 Result of removing one node by GCDN圖2 根據GCDN算法移除1個節點的結果

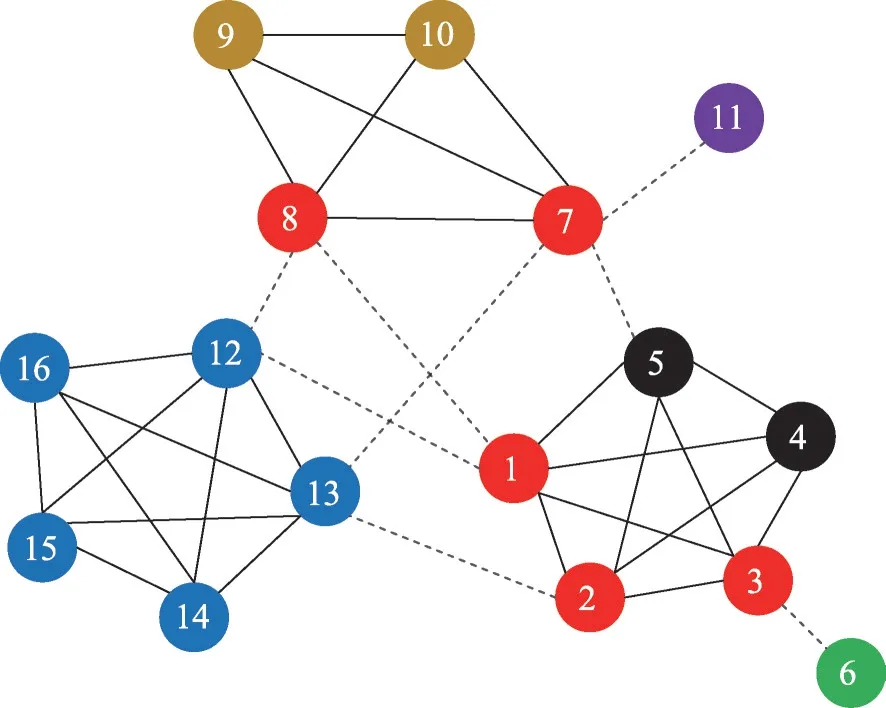
Fig.3 Result of removing 5 nodes by GCDN圖3 根據GCDN算法移除5個節點的結果

采用GCDN算法移除圖1網絡LFVC最大的5個節點后所得的社區劃分結果如圖3所示。由圖3可知，GCDN 算法將節點3誤識別為關鍵節點，并且將懸掛節點6和11移除，導致形成兩個孤立節點。同時由圖論可知，給定連通圖G，α(G)表示G的代數連通度，v為G中一個懸掛節點，有α(G)≤α(G-v)[31]。這表示從G中移除懸掛節點會增加其代數連通度，不符合GCDN算法“以最快速度減小代數連通度”的目的。

針對上述問題，本文改進GCDN社區發現算法，構建了新的關鍵節點識別與邊移除規則。

4 節點LFVC差值社區發現算法

4.1 改進的關鍵節點識別與邊移除策略

基于LFVC 的貪心社區發現算法的本質是依據節點LFVC移除網絡的邊。表2給出圖1示例網絡中關鍵節點與關鍵邊的LFVC值。

Table 2 LFVC of key nodes and edges in Fig.1表2 圖1網絡中關鍵節點與邊的LFVC

由圖1和表2可知，節點1的度為6，（1，8）與（1，12）兩條邊的LFVC 占節點1的LFVC 的64.74%，其余4條邊僅占35.26%。由此可見：LFVC 最大節點i*的鄰邊并非全都具有很高的LFVC 值，且i*的LFVC值由少數幾條重要鄰邊的LFVC 值構成。移除非關鍵鄰邊無法有效減少圖的代數連通度，還會產生大量孤立節點。為保證網絡結構信息的完整性，提高社區發現的準確率，在進行邊移除時，應當僅移除LFVC較大的邊。此外，由于移除懸掛邊并不符合使圖G的代數連通度以最快速度減小的目的，在進行邊移除操作時應保留懸掛邊。

由于關鍵邊必然是關鍵節點的鄰邊。在算法進行循環時，每移除一條邊，都會引起網絡中所有節點與邊的LFVC 值的變化。若當前LFVC 最大節點i*是關鍵節點，在與其連接的全部關鍵邊移除之前會保持較高的LFVC值，則該節點在之后的循環中容易被再次識別；若i*是非關鍵節點，則希望通過犧牲最少的網絡結構信息，即移除最小數量的邊來跳過此次循環，確保該節點在之后的循環中不易被識別，以尋找真正的關鍵節點。本文算法將LFVC 最大的兩個節點的LFVC 值之差作為決定每一次循環中所移除邊的數量的依據。

綜上所述，本文為避免GCDN 算法因移除懸掛邊與過多非關鍵邊而導致的關鍵節點識別錯誤與效率低下問題，提出如下改進的關鍵節點識別與邊移除策略：

當且僅當(i,j)*是i*的鄰邊，將i*識別為關鍵節點；計算LFVC 最大節點i*與LFVC 次大節點的差值，即，按LFVC 從大到小依次移除i*的k條鄰邊。k的計算公式如下：

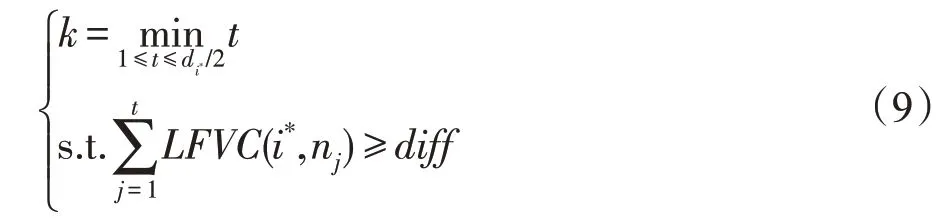
其中，(i*,nj)表示i*的LFVC值第j大的鄰邊，，表示i*的鄰接節點集；表示i*的度，din與dout分別表示與節點i*在同一個社區內部的鄰邊數目和不在同一個社區中的鄰邊數目，由于復雜網絡普遍具有“同一社區內節點聯系緊密，不同社區間節點聯系稀疏”的特性，則有，因而。

若(i,j)*不是i*的鄰邊，則僅移除(i,j)*。

由于孤立節點是因圖中懸掛邊被移除而產生，上述邊移除策略使得本文算法規避了產生孤立節點的情況。

4.2 算法設計

依據上述改進策略，本文提出節點局部Fiedler向量中心性差值社區發現算法（CDDN）。該算法分兩個階段：

階段1計算LFVC。給定循環次數q，在每次循環中識別當前規模最大的連通子圖，計算子圖的Fiedler 向量和各節點與邊的LFVC 值，找出LFVC 最大節點i*、LFVC次大節點和LFVC最大邊(i,j)*，其中i,j∈(i,j)*，di≠1且dj≠1。

階段2識別關鍵節點，依據邊移除策略對圖進行分割。

綜合上述兩個階段，本文CDDN 算法的偽代碼如下所示：

輸入：圖G，循環次數q。

輸出：社區劃分g。

4.3 算法分析

4.3.1 有效性分析

由于CDDN算法在進行邊移除時主動忽略了懸掛邊，因此可以有效避免孤立節點的生成。對圖1網絡，采用CDDN算法分別進行1次、6次循環的結果如圖4、圖5所示。其中，紅色節點是CDDN算法識別出的關鍵節點，虛線邊表示算法移除的關鍵邊。CDDN算法識別出的關鍵節點與關鍵邊均與實際相符，且不存在孤立節點。

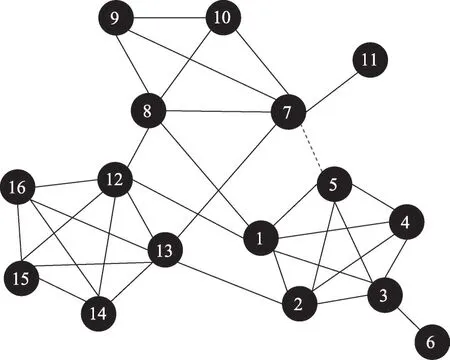
Fig.4 Result of one turn by CDDN圖4 CDDN算法進行1次循環的結果

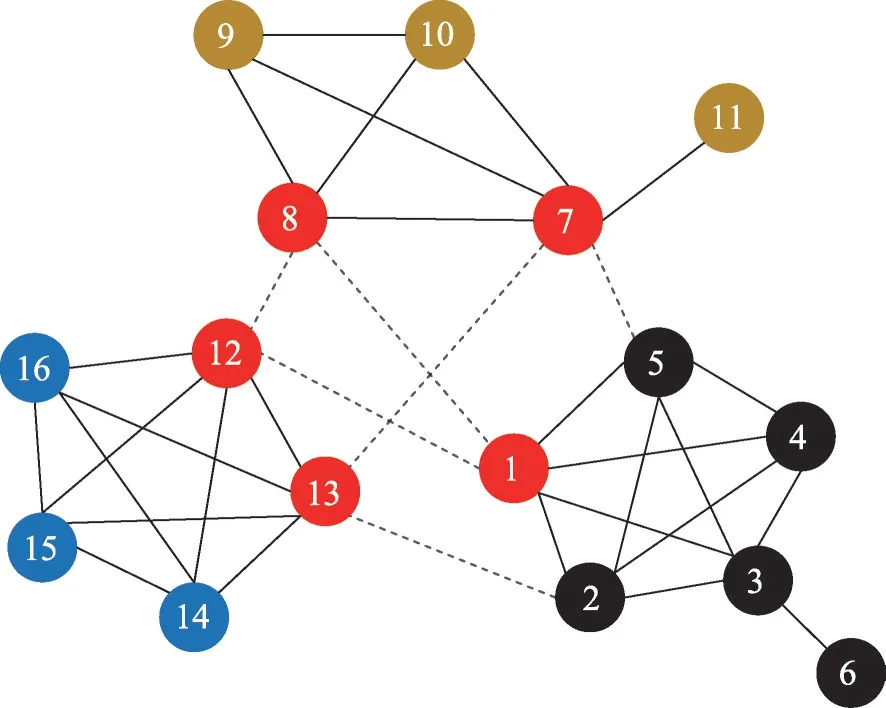
Fig.5 Result of 6 turns by CDDN圖5 CDDN算法進行6次循環的結果

當網絡中的節點較為稀疏時，CDDN算法在發現小粒度社區方面具有一定的優勢。這是由于遠離邊緣節點的節點往往具有絕對值較大的LFVC，因而對于懸掛點較多，結構較為稀疏的網絡，CDDN 算法的邊移除策略傾向于為遠離較大規模社區邊緣并與懸掛點相連接的節點分配較大的LFVC，因此這些節點易被識別為LFVC最大點，它們的非懸掛鄰邊易被優先移除，使其及其懸掛鄰點成為一個細粒度的小社區。

當網絡中的節點較為緊密時，CDDN算法通常可以發現更多的社區。CDDN 算法與GCDN 算法往往通過增加循環次數以發現更多數目的社區。一方面，在迭代過程中，GCDN 算法移除的邊大多為對圖的代數連通度影響極小的邊，而CDDN 算法在每一次循環中則是移除對圖的代數連通度影響最大的1條或k條邊。因而，在移除相同邊數的情況下，CDDN 算法發現的社區數量通常多于GCDN 算法。另一方面，由于GCDN 存在節點合并階段，導致GCDN 算法無法有效分割聯系緊密的大型網絡。相對而言由于CDDN 算法不需要節點合并的步驟，可以有效提升圖分割效率，理論上能發現更多的社區。

4.3.2 時間復雜度分析

在CDDN 算法中，步驟1為圖G的復制過程，其時間主要花費在對G中n個節點與m條邊進行復制的過程中，時間復雜度為O(n+m)。步驟3為尋找G中最大連通子圖的過程，最壞情況下其時間復雜度為O(n)。步驟4計算最大連通子圖的Fiedler 向量，基于Lanczos算法計算Fiedler向量的時間復雜度為O(m1×n)，其中m1為根據Lanczos 算法計算Laplace 矩陣的Fiedler向量的迭代次數，通常需要上百次。步驟5為計算G′中所有節點與邊的LFVC 的過程，其時間復雜度為O(m+n)。步驟6與步驟7為尋找LFVC 最大、次大非懸掛節點的過程，時間復雜度分別為O(n)和O(m)。步驟8～10為判斷并移除LFVC最大非懸掛邊的過程，時間復雜度為O(m)。步驟12、13的時間復雜度均為O(1)。步驟14～17的時間復雜度為O(r×(m+1+m))，r為 從diff=0到LFVCremove＜diff的循環次數。綜上所述，常數r,q＜＜m，CDDN 算法的最終時間復雜度為O(m1n+m)。

5 實驗結果與分析

為了驗證CDDN算法與其他現有算法在準確率和效率方面的性能，實驗用到的算法有：（1）基于全局中心性的GN算法[1]；（2）基于局部中心性的CNE算法[26]；（3）GCDN算法[28]；（4）本文所提出的CDDN算法。

表3為4種算法的時間復雜度，其中m1為Lanczos算法計算Fiedler向量所需的迭代次數，通常需要上百次。因此對于小規模網絡，CNE與GN算法可能擁有更高的效率。但對于大規模網絡，CDDN算法與GCDN算法在效率上具有明顯優勢。

Table 3 Time complexity of 4 algorithms表3 4種算法的時間復雜度

5.1 數據集

如表4所示，本文采用了4個不同規模、不同結構的真實網絡數據集（Karate、Dolphin、Football、Last.fm）進行對比實驗。其中前3個網絡已知其真實社區劃分。Karate網絡數據集[32]來自Zachary對某空手道俱樂部成員的社會關系研究。該俱樂部由于人事糾紛，最終分裂成了兩個俱樂部。Dolphin 網絡數據集[33]來自1994年至2001年期間，Lusseau及其團隊對62只寬吻海豚的觀察數據。Football網絡數據集[1]來自于2000賽季美國12個大學橄欖球隊聯盟的比賽時間表，其中節點代表球隊，邊代表兩個球隊之間進行的常規賽。Last.fm 網絡數據集來自文獻[34]所提供的在線音樂系統Last.fm的交友狀況數據。

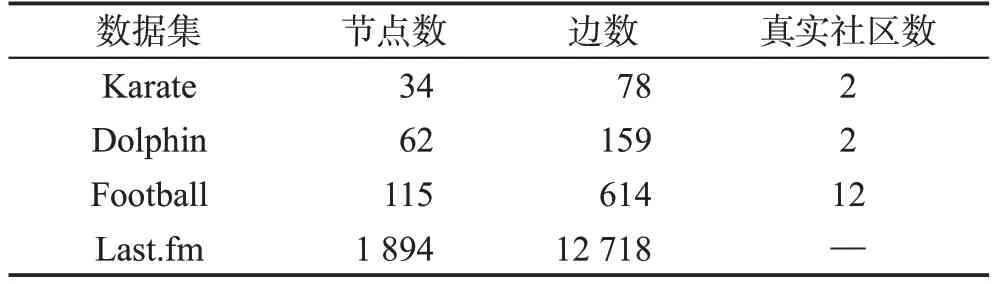
Table 4 Real network dataset表4 真實網絡數據集

5.2 評價指標

對于已知真實社區劃分的數據集，由于對比實驗的算法評價涉及孤立節點識別問題，本文采用標準化互信息（normalized mutual information，NMI）、準確率(Acc)以及忽略孤立節點時的準確率Accr、將孤立節點視為同一個社區時的準確率Accm作為社區發現算法的評價指標。給定網絡中真實社區U以及算法劃分的社區V，真實社區數為CU，劃分的社區數為CV，4個指標計算方式如下：

標準化互信息NMI(U,V)定義為[35]：

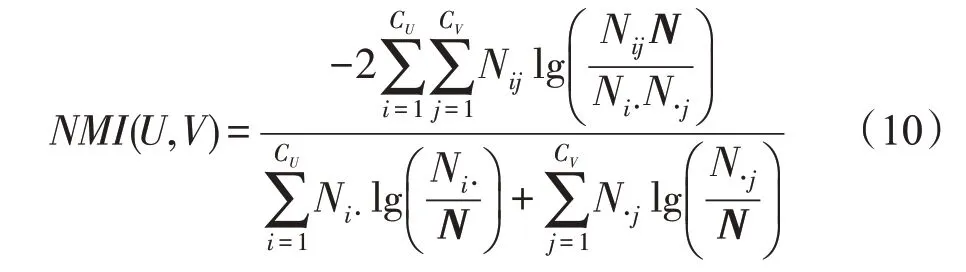
其中，N代表混淆矩陣，行表示真實社區，數目為CU，列表示劃分社區，數目為CV。Ni?表示矩陣N中第i行的和，N?j表示矩陣N中第j列的和。

算法劃分結果V的準確率（Acc）定義為：

其中，Interkt表示劃分出的某一社區vk∈V,k=1,2,…,CV與某個真實社區ut∈U,t=1,2,…,CU的交集元素的個數。

劃分的社區與真實社區的吻合程度越高，NMI和Acc的值越高。根據式（10）和式（11）可知，NMI與Acc對孤立節點具有偏好，即孤立節點的存在將提高劃分結果的NMI與準確率Acc。因而，本文針對孤立節點采取了兩種識別方式：（1）忽略所有孤立節點；（2）將所有孤立節點視為同一社區。分別計算兩種識別方式下的準確率，記為Accr和Accm。

由于無法知曉Last.fm 網絡的真實社區劃分，本文利用最大社區節點數占總節點數之比（proportion of largest community size，Plcs）與發現的社區數（detected communities，DC）來比較兩種算法在網絡劃分上的效果。

5.3 實驗結果

5.3.1 Karate網絡

該數據集包含34個節點，真實社區數為2，為了分析算法發現更小粒度社區的表現，圖6～圖8顯示了4種算法分別發現2～5個社區時的NMI、忽略所有孤立節點時的算法準確率Accr、將孤立節點視為同一社區時的算法準確率Accm。CNE算法在該數據集上僅能發現兩個社區，使用其發現兩個社區時的數據對其發現3～5個社區時的數據進行填補。

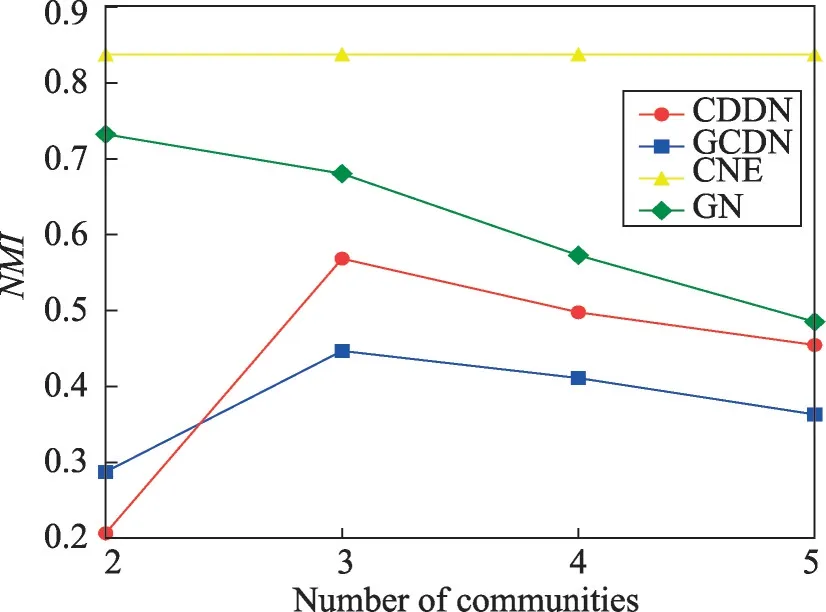
Fig.6 NMI on Karate network圖6 在Karate網絡上的NMI

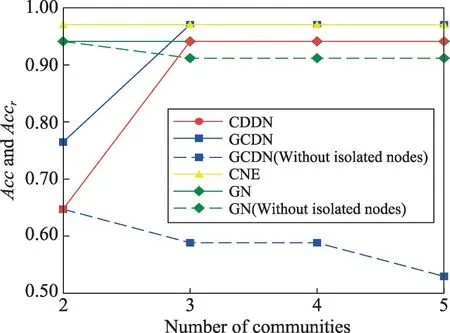
Fig.7 Acc and Accr on Karate network圖7 在Karate網絡上的Acc與Accr

如圖6所示，由于Karate 網絡規模較小，在該數據集上GN 算法與CNE 算法的準確性均優于CDDN算法與GCDN 算法。將Karate 網絡劃分為兩個社區時，CDDN算法的NMI略低于GCDN算法，當將網絡劃分為更多細粒度的社區時，CDDN 算法的NMI高于GCDN算法。由于NMI和準確率Acc對孤立節點具有偏好性，而GCDN 算法會隨著劃分社區數的增多產生越來越多的孤立節點，因而在圖7、圖8中，當不對孤立節點產生的影響進行處理時，GCDN算法的準確率Acc相對較高。而在考慮孤立節點帶來的影響并進行相應處理之后，CDDN 算法所獲得的Accr和Accm明顯優于GCDN算法。

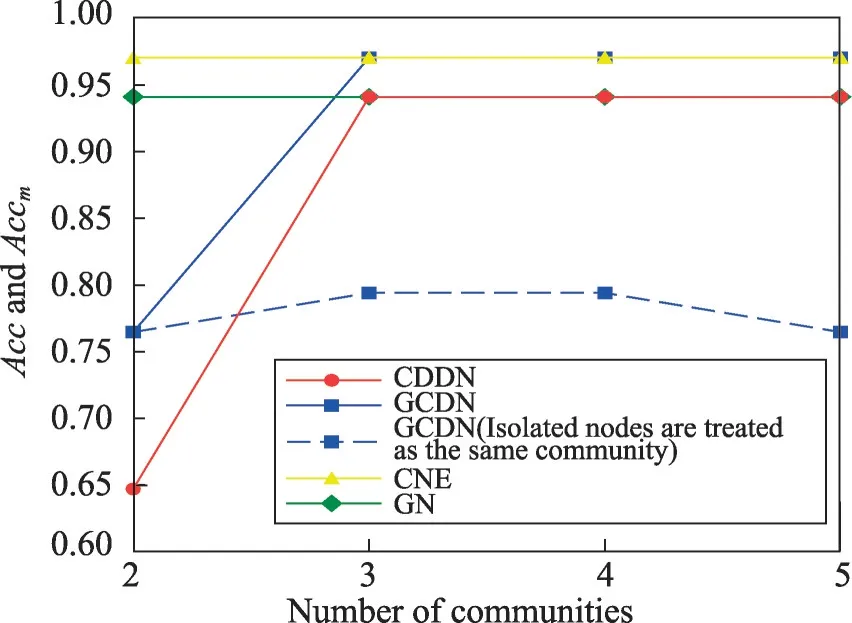
Fig.8 Acc and Accm on Karate network圖8 在Karate網絡上的Acc與Accm

5.3.2 Dolphin網絡

該網絡具有兩個真實社區，圖9展示了CDDN算法將該網絡劃分為兩個社區時的結果。其中黃色代表劃分錯誤的節點，紅色代表算法發現的關鍵節點，藍色與綠色節點分別代表兩個不同的社區。與真實社區相比，CDDN 算法僅有一個節點劃分錯誤，說明了使用CDDN算法進行社區劃分的有效性。

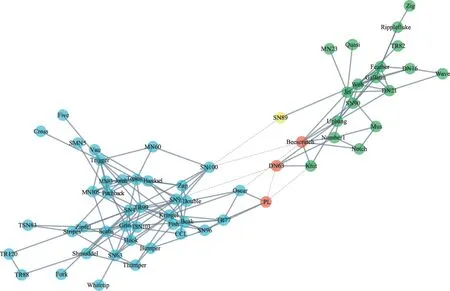
Fig.9 Partition Dolphin network to 2 communities by CDDN圖9 CDDN算法將Dolphin網絡劃分為兩個社區的結果

圖10～圖12給出了4種算法在Dolphin網絡上發現2～7個社區時的NMI、Accr和Accm。需要說明的是，由于GCDN 算法無法發現數量為5和7的社區，為了填補缺失值，繪圖時分別用數量為4和6時的數據替代。由圖10所示，CDDN 算法在發現2～7個社區時，所獲得的NMI均大于其他3種算法。如圖11、圖12所示，CDDN算法與GN算法在發現兩個社區時已經具有很高的準確率，當發現社區數目為2～7個時所獲得的準確率Acc值均較高，且呈現穩定狀態。而GCDN 算法和CNE 算法準確率不僅低于CDDN 和GN算法，而且曲線呈現一定波動性。當考慮孤立節點所帶來的影響并進行相應處理之后，CDDN算法的優勢更為明顯。

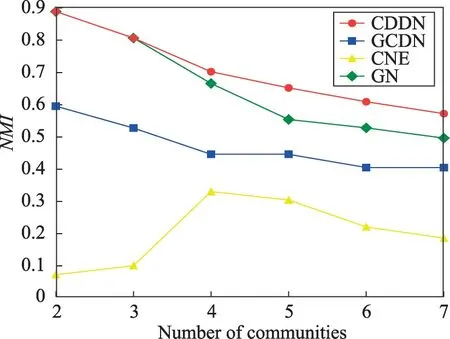
Fig.10 NMI on Dolphin network圖10 在Dolphin網絡上的NMI

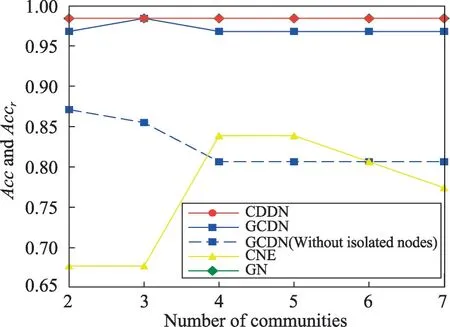
Fig.11 Acc and Accr on Dolphin network圖11 在Dolphin網絡上的Acc與Accr

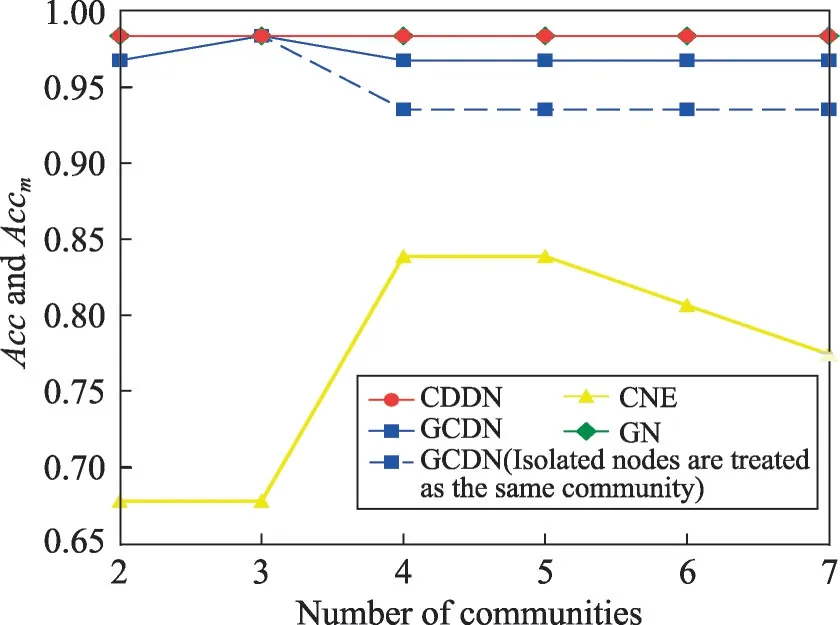
Fig.12 Acc and Accm on Dolphin network圖12 在Dolphin網絡上的Acc與Accm

5.3.3 Football網絡

較前兩個網絡而言，Football網絡規模更大，真實社區數更多。GCDN 算法對該網絡進行劃分沒有產生孤立節點。表5展示了4種算法劃分出同樣數量社區時所需移除的最小邊數。由表5可知，當劃分出相同數量社區時，CDDN 算法所移除的邊數略多于GN算法，且遠遠小于GCDN算法與CNE算法所移除的邊數。這說明CDDN 算法顯著提升了圖分割效率。圖13、圖14給出了實驗對比4種算法在發現4～12個社區時的NMI與Acc。表6給出了4種算法對Football 網絡進行社區發現時，發現各個數量的社區所需的運算時間。由圖13、圖14可知，在發現各數量的社區時，CDDN 算法的NMI值和準確率Acc均明顯優于GCDN 算法與CNE 算法，略優于GN 算法。結合表6可得，雖然CDDN算法的準確率與GN算法大致相同，但算法花費時間遠少于GN 算法，效率上明顯優于GN算法。此外值得注意的是，GCDN算法與CNE 算法至多只能發現該網絡中的9個社區，無法發現全部社區，而CDDN與GN算法卻可以獲得全部社區結構。圖15展示了使用CDDN 算法劃分Football網絡所獲得的12個社區。

Table 5 Number of edges removed by 4 algorithms on Football network表5 在Football網絡上4種算法移除的邊數

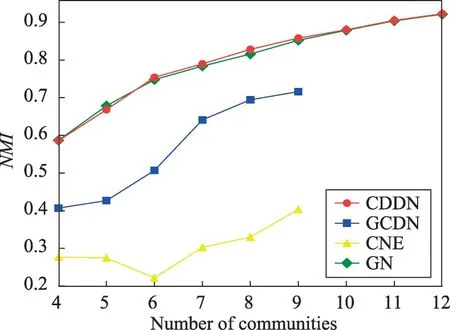
Fig.13 NMI on Football network圖13 在Football網絡上的NMI

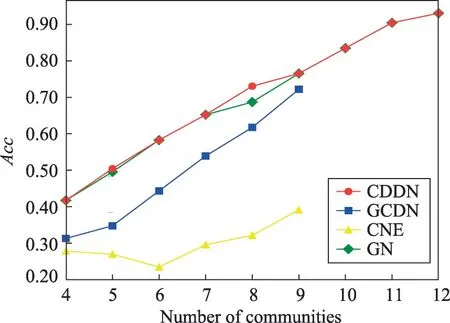
Fig.14 Acc on Football network圖14 在Football網絡上的準確率Acc

Table 6 Running time of 4 algorithms on Football network表6 在Football網絡上4種算法的運行時間

5.3.4 Last.fm網絡

表7展示了4種算法對Last.fm 網絡進行劃分所需的時間，由于GN算法需要將網絡中的每一條邊均移除后才可得出結果，故只有一個時間數據；CNE算法無法在限定時間內運行完畢，導致了數據的缺失。從表7中可看出，CDDN算法在處理大規模網絡時，效率明顯優于其余3種算法。此處僅用運行時間與本文提出的CDDN算法相近的GCDN算法進行社區發現結果的比較。圖16展示了CDDN 算法與GCDN算法在移除相同邊數時，網絡中最大社區規模占總規模之比Plcs。如圖16所示，相對于GCDN 算法，CDDN 算法對應的曲線下降速度更快，說明CDDN 算法可以在移除較少邊數的情況下就達到GCDN算法的社區劃分效果，其分割網絡的效率高于GCDN算法。圖17展示了兩種算法在移除相同邊數時發現的社區數量的對比結果。如圖17所示，CDDN 與GCDN 算法在移除相同邊時，CDDN 算法發現社區數目明顯多于GCDN 算法，且能發現更多細粒度的社區，說明CDDN 算法的社區發現能力優于GCDN 算法，同時也印證了相對于GCDN 算法，CDDN算法在社區劃分效率上更具優勢。

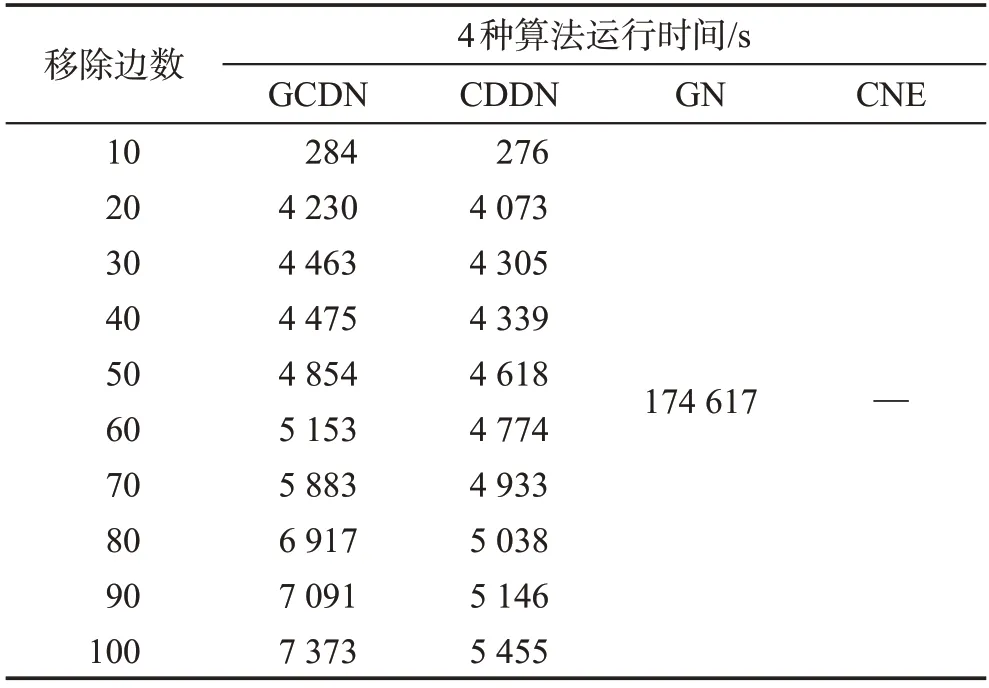
Table 7 Running time of 4 algorithms on Last.fm network表7 在Last.fm網絡上4種算法的運行時間

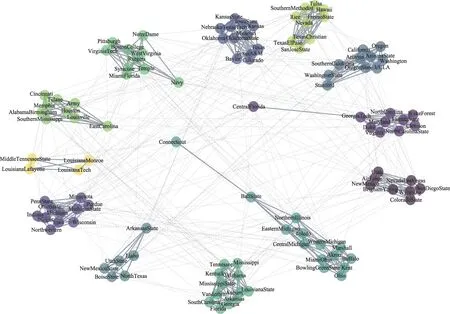
Fig.15 Partition Football network to 12 communities by CDDN圖15 CDDN算法將Football網絡劃分為12個社區

Fig.16 Proportion of largest community size to total size(Plcs)圖16 最大社區規模占總規模之比（Plcs）

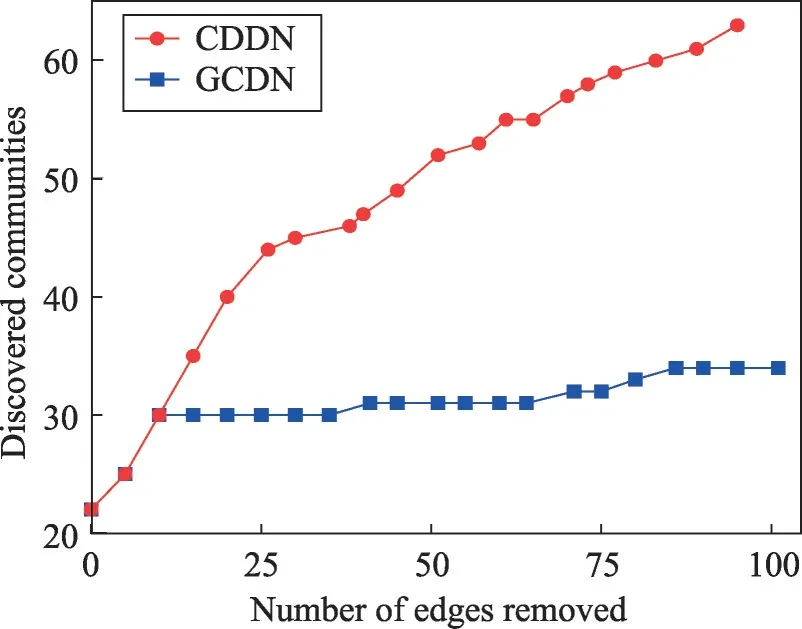
Fig.17 Number of detected communities(DC)圖17 發現的社區數量（DC）

6 結束語

本文通過分析復雜網絡拓撲結構對局部Fiedler向量中心性的影響，提出了節點局部Fiedler 向量中心性差值社區發現算法，有效解決了GCDN 算法中存在的關鍵節點和關鍵邊的識別失誤問題以及孤立節點問題。在Karate、Dolphin、Football、Last.fm 四個真實網絡上的對比實驗表明，相對于其他三種相關算法，本文算法的效率與準確率均有顯著提升。