時頻聯合長時循環神經網絡

莊連生 呂 揚 楊 健 李厚強

1(中國科學技術大學信息科學技術學院 合肥 230027)2(軍事科學院系統工程研究院 北京 100191)3(鵬城實驗室 廣東深圳 518000)(lszhuang@ustc.edu.cn)

時間序列建模是機器學習領域的一個研究熱點,廣泛應用于股票行情分析、語音識別、腦電分析等領域[1].近年來，得益于海量數據資源的出現和計算資源的提升，以循環神經網絡[2](recurrent neural network,RNN)為代表的深度學習技術被廣泛應用于時間序列模型中，并在一些特定領域取得了巨大的成功(如語音識別).但是，現有循環神經網絡仍然存在著3個問題：

1)難以捕獲時間上的長期依賴關系.經驗表明，RNN只能處理不超過200個時間步的時間序列數據之間的依賴關系，難以滿足實際應用需要；

2)多數RNN網絡只考慮了對時域信息建模，忽略了對頻域信息建模，而頻率是描述和分析時間序列的一個重要工具；

3)傳統循環神經網絡及其變體通常只能疊加2～3層，繼續疊加反而會造成性能下降，不利于擬合復雜函數.這些缺陷限制了現有循環神經網絡的性能，尤其是處理一些具有長時依賴關系且頻率成分比較豐富的時間序列的時候.

針對上述問題，研究人員從不同角度對RNN網絡進行改進和探索.為提高神經網絡對長時依賴關系的建模能力，研究人員先后提出了長短期記憶網絡[3](long short-term memory,LSTM),Peephole LSTM[4],GRU[5](gated recurrent unit),CW-RNN[6](clockwork RNN)等.最近，Li等人[7]提出一種獨立循環神經網絡(independently recurrent neural network,IndRNN)模型，通過解耦隱藏層神經元和引入修正線性單元(rectified linear unit,ReLU)，維持網絡的長期記憶，并可以疊加多層，更加容易訓練成深層神經網絡.但是，IndRNN僅考慮了時域特征模式，沒有考慮頻域特征模式.因此，當輸入數據存在豐富的頻率成分時，比如對股票交易數據、音位數據建模時，IndRNN模型反而不如其他簡單的算法性能更好.

事實上，如果要對時間序列進行分類或預測，對頻率成分的建模起著非常重要的作用[8].例如在音位分類問題中，像“p”，“t”這樣的音位是由短而高頻的信號產生的，而“iy”，“ey”等音位則與較長的低頻信號有關.建模頻域特征對于正確識別語句中的音位是相當有用的.類似地，在預測問題中，音樂片段通常由跨越頻段的不同頻率組成，所以自動生成音樂片段的剪輯通常需要適當地對高頻和低頻成分進行建模[8].此外,對特定物體進行跟蹤也是一個經典的預測問題，特定物體跟蹤問題可以表述為利用物體運動觀察量持續預測某物體的實際位置，從信號處理的角度考慮，提取物體運動的觀察量在某些頻率上的特征和分析物體運動周期對于預測物體位置非常重要.此外，對社會現象進行分析或預測時，也應該考慮時間序列的頻域特征模式.舉例來說，在對交通流量數據進行分析時，工作日和雙休日周期、早高峰和晚高峰周期，對于分析交通流量數據都尤為重要.因此，對時間序列中的頻域特征模式建模，是正確分析時間序列數據的關鍵.基于上述觀察，Hu等人[8-9]提出了一種狀態頻率記憶循環神經網絡(state frequency memory recurrent neural network,SFM-RNN)，通過多頻率狀態記憶實現對頻域特征模式的提取.但是，SFM-RNN模型基于LSTM的門實現對高低頻的選擇，并不能有效地對長時依賴關系進行建模.事實上,我們的實驗也表明SFM-RNN模型只能疊加1～2層，無法訓練深層網絡.

受IndRNN和SFM-RNN啟發，本文提出一種新型循環神經網絡結構——時頻聯合長時循環神經網絡(long term recurrent neural network with state-frequency memory,LTRNN-SFM).該網絡通過將傳統信號分析手段引入到循環神經網絡中，即通過將循環神經網絡隱藏層的狀態向量替換為狀態-頻率矩陣，聯合捕獲時間序列時域特征模式和頻域的特征模式.同時，通過解耦隱藏層的神經元、引入非飽和激活函數ReLU和權重裁剪，有效地避免了梯度消失和梯度爆炸問題，既可以使網絡維持長期記憶，又可以使深層網絡更加容易訓練.LTRNN-SFM借鑒了SFM-RNN和IndRNN的核心思想,在保留了兩者優點的基礎上巧妙避開了各自缺陷.最終，LTRNN-SFM比SFM-RNN模型更簡單，也取得了比IndRNN更強的表達能力.最終實驗表明:LTRNN-SFM在時間序列分類任務上性能更好，更適合處理長時依賴且頻率豐富的時間序列.

1 相關工作

1.1 IndRNN模型

Li等人[7]提出的IndRNN模型通過解耦隱藏層神經元、引入激活函數ReLU和權重裁剪，較好地避免了梯度消失和梯度爆炸問題，可以實現對具有長時間依賴關系的時間序列數據的有效建模.實驗表明:IndRNN模型可以處理超過1 000個時間步的時間序列,并更容易堆疊得到深層網絡.

IndRNN模型可以描述為

ht=σ(Wxt+u⊙ht-1+b),

(1)

其中，⊙代表矩陣的哈達瑪積(Hadamard product)運算，這使得隱藏層中的神經元之間是相互獨立的；σ代表激活函數ReLU.圖1描述了基礎IndRNN[7]模型結構.

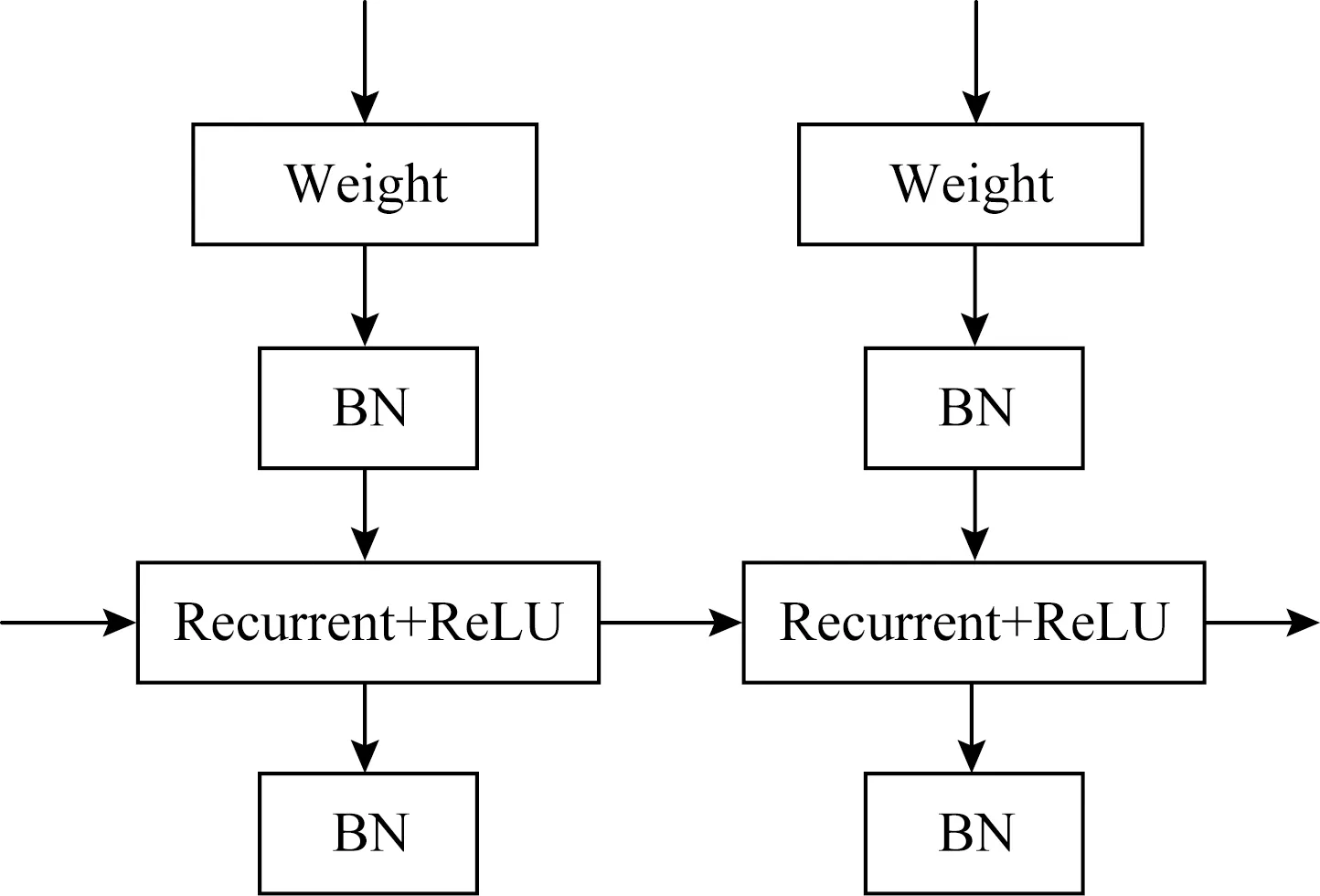
Fig.1 Basic IndRNN architecture圖1 基礎IndRNN模型結構

對于第n個神經元，隱藏層的狀態hn,t可以描述為

hn,t=σ(wnxt+unhn,t-1+bn),

(2)

其中,wn和un分別是輸入權重矩陣的第n行和隱藏層權重向量的第n個元素，隱藏層的每個神經元只接收來自該時間步的輸入信息和前一時間步隱藏層對應神經元的狀態，即IndRNN模型中的每個神經元可以獨立處理一種時間-空間特征模式，其中wn負責提取輸入信息的空間特征，un負責提取來自上一時間步的時間特征.

IndRNN模型提出了隱藏層中各神經元獨立提取時間-空間特征的新視角.不同神經元間的特征融合可以通過多層網絡結構的堆疊實現，在這種情況下，上一層隱藏層的所有神經元的輸出將作為下一層隱藏層每個神經元的輸入.

IndRNN模型所使用的ReLU激活函數，不但改善了隱藏層內的梯度消失，也改善了隱藏層間的梯度消失，使IndRNN模型可以實現多層疊加.文獻[7]證明了一層隱藏層權重是可對角化矩陣、激活函數是線性函數的傳統RNN模型與2層IndRNN模型等價.此外，在多層疊加的IndRNN模型中，隱藏層之間是全連接的形式，因此也可以引入批量歸一化(batch normalization，BN)等連接方式.

1.2 SFM-RNN模型

為了對時間序列進行多頻率分析，Hu等人[8]提出了SFM-RNN模型，以捕捉輸入時間序列的時域和頻域特征.

SFM-RNN模型將LSTM模型的狀態向量存儲單元替換為狀態-頻率矩陣存儲單元，對于預測和分類任務，通過門選擇適當的狀態-頻率成分，決定應該選擇哪些成分來預測輸出信息或作為分類的依據.

SFM-RNN模型的狀態-頻率矩陣可由離散傅里葉變換得到:

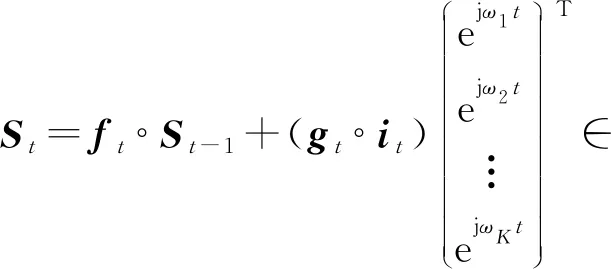
(3)

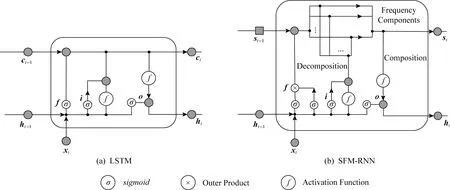
Fig.2 Comparison between the cell structures of the LSTM and the SFM-RNN圖2 LSTM和SFM-RNN網絡單元結構對比圖

此外，SFM-RNN模型能以自適應方式確定頻率.具體而言，可以將頻率定義為與每個時刻輸入信息和存儲單元相關的函數，使模型自動學習對應的頻率.

2 時頻聯合長時循環神經網絡

本文提出的時頻聯合長時循環神經網絡模型(LTRNN-SFM)借鑒了SFM-RNN模型和IndRNN模型的核心思路，有效保留了這2個模型的優點,巧妙避免了現有循環神經網絡存在的主要問題.其基本思想是：通過將傳統循環神經網絡隱藏層的狀態向量替換為狀態-頻率矩陣，聯合捕獲時間序列時域和頻域的特征模式；通過解耦隱藏層神經元、引入非飽和激活函數ReLU和權重裁剪，有效地避免了梯度消失和梯度爆炸問題，既可以使網絡維持長期記憶，又可以訓練深層網絡.

假設一個時間序列數據集中有M條時間序列，根據某個時間點上觀測變量的數量，可以將時間序列劃分為單變量時間序列和多變量時間序列[1].本文提出的時頻聯合長時循環神經網絡可以處理單變量時間序列和多變量時間序列.

本文設計了2種網絡結構，單層時頻聯合長時循環神經網絡和多層時頻聯合長時循環神經網絡，均可以應用于分類和預測問題.在具體應用中，基于不同的應用場合和目的，可以采用不同層數的網絡結構.采用的層數越多，越能擬合復雜函數.

2.1 單層時頻聯合長時循環神經網絡

通過網絡結構和梯度問題2個方面闡述單層時頻聯合長時循環神經網絡.

1)網絡結構

單層時頻聯合長時循環神經網絡可以描述為

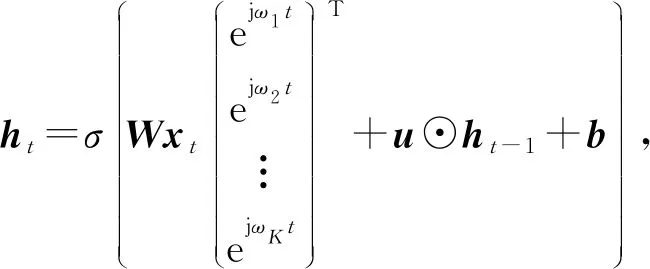
(4)

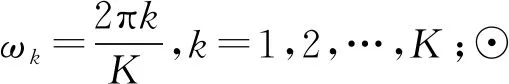
隱藏層的狀態-頻率矩陣可以分解為實部和虛部：

Reht=σ(Wxt[cosω1t,cosω2t,…,cosωKt]+
u⊙Reht-1+b),

(5)

Imht=σ(Wxt[sinω1t,sinω2t,…,sinωKt]+
u⊙Imht-1+b),

(6)

(7)

其中,(·)2代表該矩陣對應元素的平方.

ht的相位被定義為

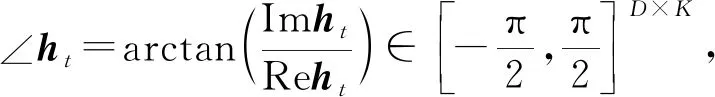
(8)

其中,arctan(·)是對矩陣中每個元素進行反正切變換.

在最后一個時間步，根據式(7)求出隱藏層的狀態-頻率矩陣的幅度，作為預測或分類任務的依據，其中相位信息由于不影響最終結果被忽略.

如2.1節所述，在對時域和頻域的特征模式聯合建模時，在每個時間步，輸入信息都分解到K個頻率維度上.隱藏層的所有神經元共同構成狀態-頻率矩陣，以維持多頻率狀態記憶.對于狀態-頻率矩陣中的每個元素，用矩陣的行檢索不同的狀態，每個狀態能理解為引發信號的某種物理因子.與此類似，用矩陣的列索引不同頻率分量，表示不同因子對不同頻率分量的影響程度.由于隱藏層神經元已經被解耦，神經元之間相互獨立，下一時間步的神經元僅會接受上一時間步對應神經元的輸出，每個神經元可以獨立地處理一種狀態-頻率-時間模式，提高了神經元的可解釋性.

2)梯度問題

正是由于時頻聯合長時循環神經網絡隱藏層神經元之間相互獨立，有效地避免了傳統循環神經網絡中的梯度消失和梯度爆炸問題.

具體而言，在誤差反向傳播過程中，由于隱藏層中神經元沒有相互聯系，因此可以對每個神經元獨立計算梯度.

矩陣中第n行、第k列元素對應的神經元描述為

hn k,t=σ(wnxtejωkt+un khn k,t-1+bn k),

(9)

對于神經元hn k,假設時刻T的優化目標是Jn k,則反向傳播到時刻t的梯度為

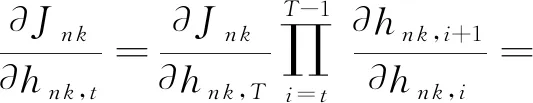
(10)

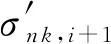
2.2 深層時頻聯合長時循環神經網絡

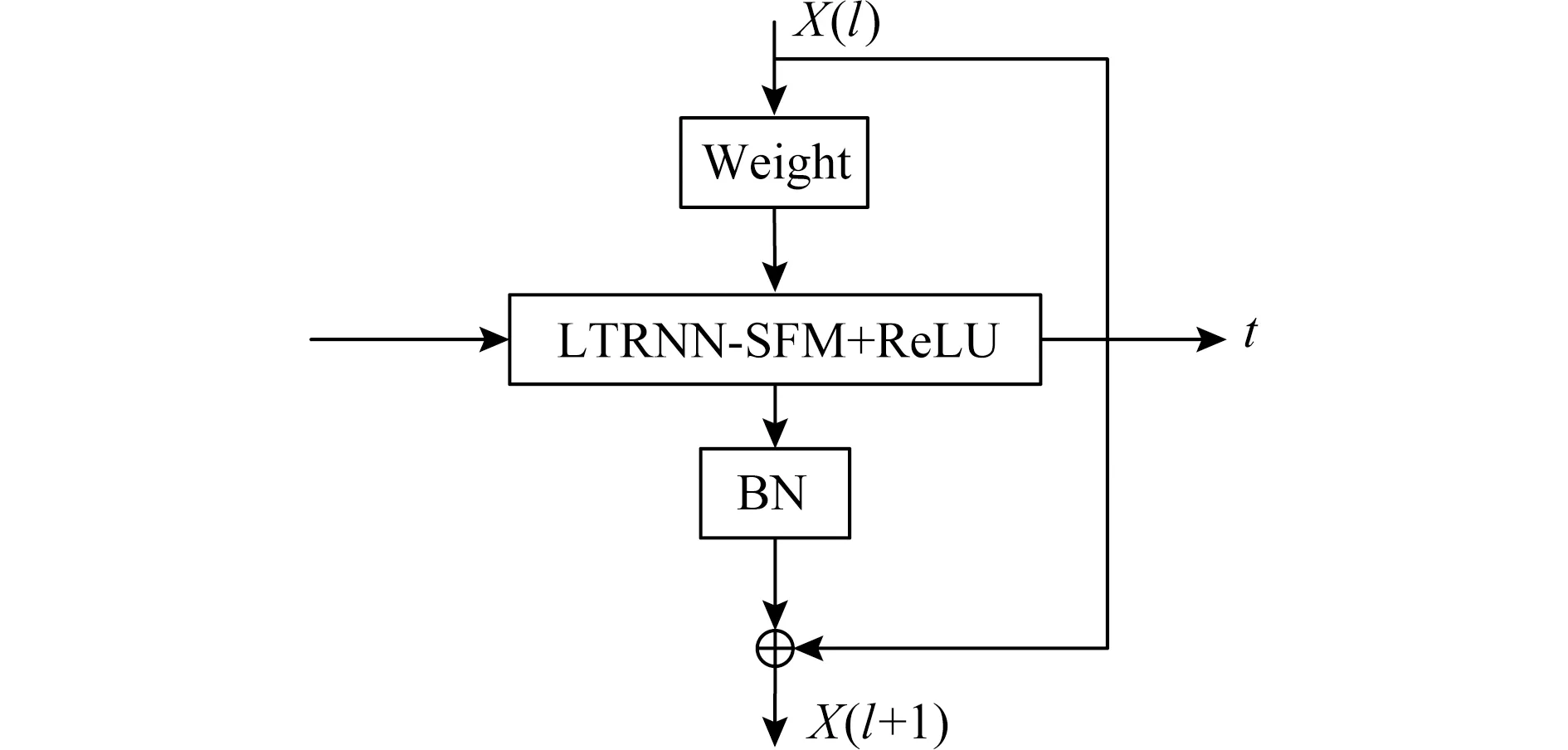
Fig.3 Illustration of the residual LTRNN-SFM architecture圖3 引入殘差連接的時頻聯合長時循環神經網絡示意圖

深層時頻聯合長時循環神經網絡可以通過單層時頻聯合長時循環神經網絡疊加而成.網絡疊加有助于擬合更加復雜的函數.

傳統循環神經網絡及變體(如RNN和LSTM)的激活函數主要基于sigmoid和tanh，一般只能疊加2～3層，再往上疊加性能反而下降，這是由于sigmoid和tanh的梯度在飽和區域非常平緩，從而造成層間梯度消失.而深層時頻聯合長時循環神經網絡由于使用了非飽和函數ReLU，可以有效緩解層間的梯度消失問題.此外，BN層的應用也較好地改善了深層神經網絡的梯度問題.

和IndRNN模型類似，在時頻聯合長時循環神經網絡中，隱藏層之間也是全連接的形式，因此同樣可以引入BN等連接方式.圖3為引入殘差連接的多層時頻聯合長時循環神經網絡示意圖.

圖3中“Weight”和“LTRNN-SFM+ReLU”分別表示對輸入數據的處理和每個時間步的隱藏層神經元的處理.

2.3 應用場景

時頻聯合長時循環神經網絡的應用如圖4所示:

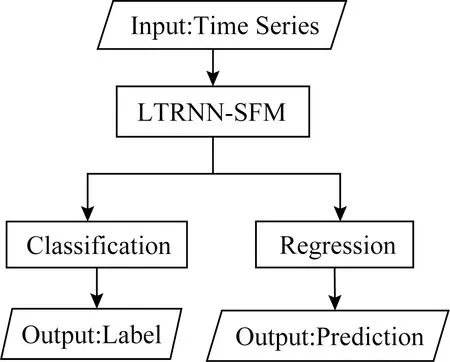
Fig.4 Applications of LTRNN-SFM圖4 時頻聯合長時循環神經網絡的應用

1)時間序列預測任務

假設訓練集有M條單變量時間序列，第m條時間序列表述為{zm,t|t=1,2,…,T}，n步預測任務定義為根據前t個時間步的序列對t+n時間步的值zm,t+n進行預測[5]：

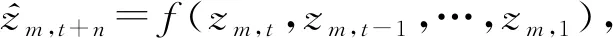
(11)

其中,f表示從歷史信息預測n個時間步后信息的函數映射.時頻聯合長時循環神經網絡即等價于式(11)中f映射.

在時頻聯合長時循環神經網絡的預測任務中,網絡的訓練分為2個階段：

① 前向傳播階段.對時間序列預測時，將時頻聯合長時循環神經網絡最后一個時刻的隱藏層的狀態-頻率矩陣ht的幅度|ht|，作為全連接層的輸入，并通過全連接層將矩陣壓縮得到n步預測值.

② 反向傳播階段，即誤差傳播階段.最小化訓練集中預測值和真實值間的平方差之和進行訓練：

(12)

網絡中所有參數通過基于時間的反向傳播(back-propagation through time,BPTT)算法進行更新.

2)時間序列分類任務

假設一個時間序列數據集中有M條多變量時間序列，即D={V1,V2,…,VM}，每條時間序列有T個觀測點和一個類標簽，即第m條時間序列可以表示為Vm=〈vm,1,vm,2,…,vm,T,cm〉.時間序列分類任務可以定義為將時間序列的一組觀測值映射為類標簽[1].

在時頻聯合長時循環神經網絡分類問題中,網絡的訓練分為2個階段：

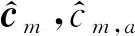
(13)

在分類任務中，得到最大概率的類標簽作為網絡輸出的預測類標簽.

② 反向傳播階段，即誤差傳播階段.計算實際輸出類標簽和理想類標簽的交叉熵代價函數，并按照最小化交叉熵的方法調整權重矩陣.

交叉熵代價函數：

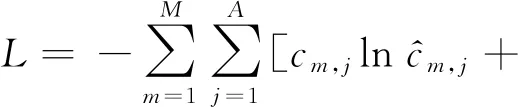
(14)

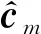
3 實驗結果和分析

為驗證本文所提出的時頻聯合長時循環神經網絡的性能，下面將網絡應用于SKLearn(scikit-learn)手寫數字數據集分類任務、人體動作識別數據集分類任務和手勢階段數據集分類任務中.

3.1 SKLearn手寫數字數據集分類

SKLearn是基于Numpy和Scipy的一個機器學習算法庫，其中包含了大量優質的數據集.本實驗選取的是SKLearn中的手寫數字數據集[10].該數據集共有1 797個樣本，樣本示例如圖5所示.其中每個樣本對應一張手寫數字圖像和一個0～9整數的標簽，圖片分為10類，即手寫數字0～9.不同于MNIST手寫數字數據集，SKLearn中的每張手寫數字圖像大小為8×8像素，這使識別更加困難，對算法要求更高.數據集被隨機劃分為測試集和訓練集，其中訓練集占80%，測試集占20%.

為了將圖像分類問題轉換為時間序列分類問題，每張手寫數字圖片被視為一串時間序列，該序列有8個觀測點，每個觀測點有8個觀測變量，即一個多變量時間序列.具體而言，每張圖片以矩陣的形式存儲，如圖5所示，其中矩陣中每行對應每個觀測時間點，行中每個元素對應每個觀測變量.

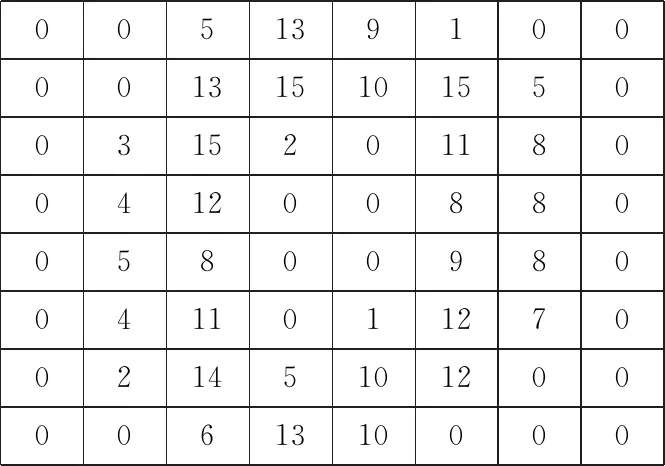
0051391000013151015500315201180041200880058009800411011270021451012000061310000

Fig.5 Example of SKLearn hand-written digital dataset圖5 SKLearn 手寫數字數據集示例

實驗中采用的對比模型包括LSTM[3],IndRNN[7],SFM-RNN[8]以及本文提出的LTRNN-SFM.對于IndRNN，LSTM，LTRNN-SFM，由于2層模型的性能明顯優于單層模型，因此本實驗基于2層堆疊的網絡結構.對于SFM-RNN模型，2層SFM-RNN的性能反而比單層SFM-RNN模型有明顯下降，甚至由于每次初始化不同，模型可能無法收斂，因此實驗采用單層SFM-RNN模型.這種設置保證了每種模型有最佳性能表現，保證了比較的公平性.

圖6顯示了4種模型在測試集上的分類正確率，這里模型訓練的輪數為500輪.

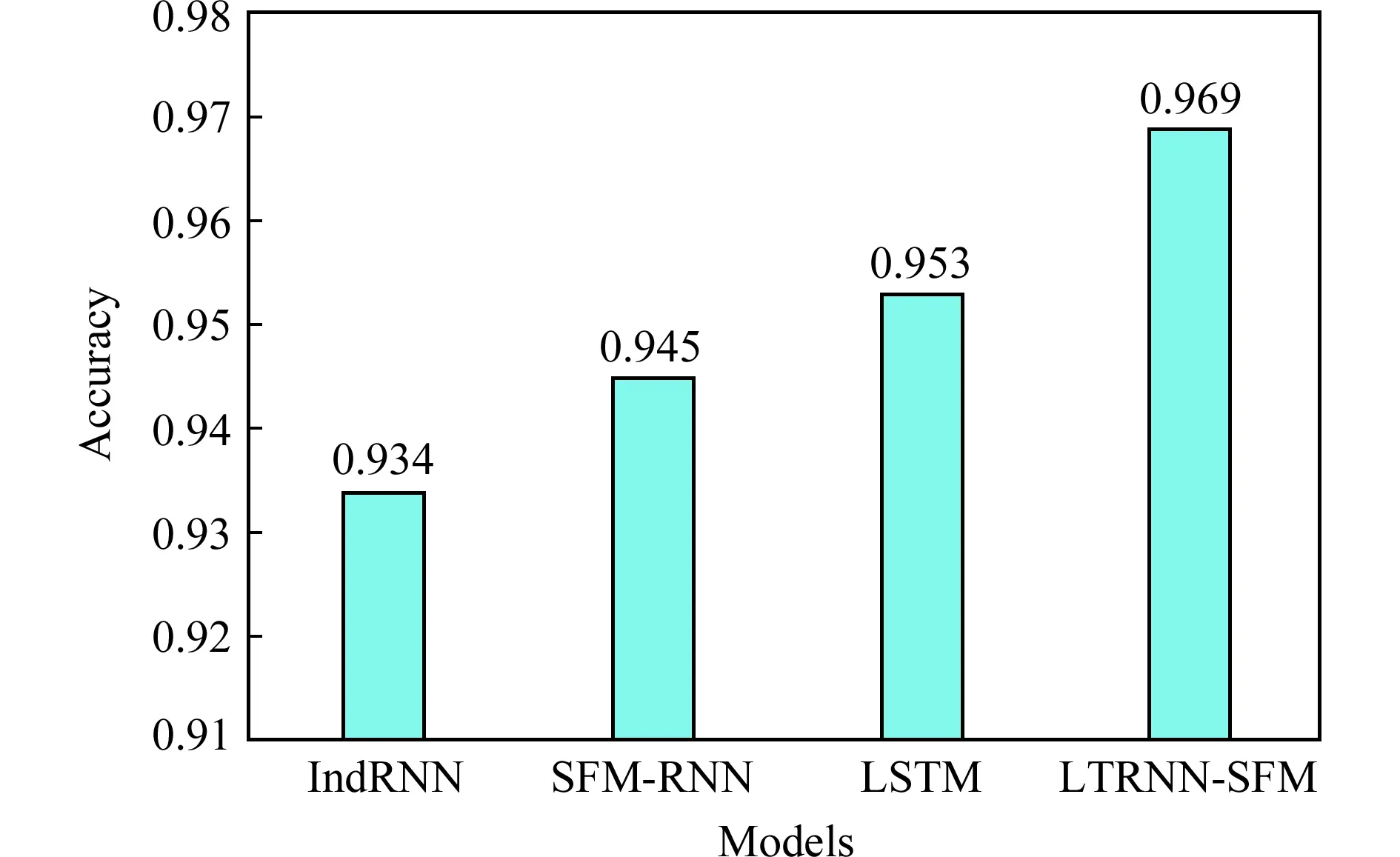
Fig.6 Experimental results for the hand-written digital dataset圖6 手寫數字數據集實驗結果

由圖6可知，LTRNN-SFM模型的性能明顯優于IndRNN,LSTM,SFM-RNN.該實驗結果也驗證了2.1節對模型的分析，即對分辨率較低的圖片進行分類時，LTRNN-SFM由于引入了多頻率分析，而不只是時域一個維度，與只考慮了時域信息的神經網絡模型(IndRNN,LSTM)相比，性能有一定的提高.這里需要指出的是，IndRNN模型性能表現比SFM-RNN和LSTM還差.這主要是因為，IndRNN適合處理長時依賴關系的時序數據，而本實驗中每張圖像轉換為時序數據長度僅為8，并不能體現出模型適合長時依賴的優勢.從這個結果同時可以看出，本文所提出的算法對于短時序列也是有效的，體現了LTRNN-SFM模型的魯棒性.

3.2 UCI-HAR數據集分類

本實驗使用UCI人體動作識別數據集(UC Irvine machine learning repository-human activity recognition,UCI-HAR)[11]來驗證模型的有效性.該數據集的來源是30名年齡在19～48歲之間的志愿者，每個人在腰上佩戴智能手機(三星Galaxy S II)進行了6項活動(步行、站立、坐、躺、上樓、下樓)，通過嵌入式加速度計和角速度計，研究人員以50 Hz的恒定速率捕獲3個軸方向的線性加速度和3個軸方向的角速度.這些實驗已經過視頻記錄以手動標記數據.所獲得的數據集已被隨機分成2組，其中70%的志愿者被選中用于生成訓練數據，其余30%的志愿者生成測試數據.實驗選擇了未提取特征的完整原始傳統信號，共10 299個樣本，其中訓練集有7 352個樣本，測試集有2 947個樣本.每個樣本可以被視為一條有128個觀測時間點的多變量時間序列，每個觀測點有9個觀測變量.

實驗比較了4種模型(LSTM[3],IndRNN[7],SFM-RNN[8],LTRNN-SFM)在UCI-HAR數據集上的性能，網絡結構與3.1節實驗相同，模型訓練輪數設置為1 000輪.實驗結果如圖7所示:

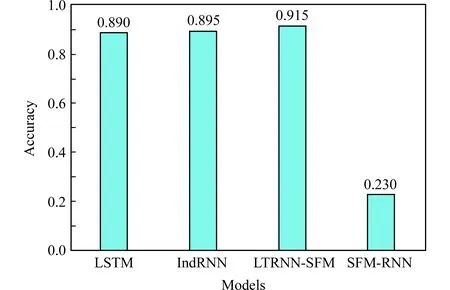
Fig.7 Experimental results for the UCI-HAR dataset圖7 人體動作識別數據集UCI-HAR實驗結果

由圖7可知，LTRNN-SFM,IndRNN,LSTM三者在測試集上的正確率相差不大，但是SFM-RNN性能表現卻比較糟糕.這可能是因為SFM-RNN模型大量使用了sigmoid,tanh飽和激活函數，導致在較長的時間序列中，會造成梯度消失/爆炸的問題.對于IndRNN和LSTM兩種模型，由于沒有考慮到頻率特征模式，使得其性能也稍遜于本文的LTRNN-SFM.

3.3 手勢階段數據集分類

為了進一步驗證LTRNN-SFM模型捕捉長時依賴關系的能力，本實驗選擇了UCI手勢階段分類數據集[12].該數據集是用Kinect采集的多人動態手勢庫，旨在實現非特定人的動態手勢識別，以提高視頻預處理能力.采集的數據包括6個關節點(左手、右手、左手腕、右手腕、頭部、脊柱)對應的位置(坐標x,y,z).具體而言，3位志愿者被要求閱讀3個漫畫,并用手勢講述漫畫內容，其中包括志愿者A講述故事1,2,3，志愿者B和志愿者C講述故事1和故事3.最后由手勢研究人員對文件進行手動分割，將所有文件分為5個不同的階段.本實驗采用的數據集為UCI數據集的子集[13],并選取了未提取特征的原始信號，所獲得的數據集被隨機分為2組，共396個樣本，其中80%的數據被用于訓練，20%的數據被用于測試，屬于小樣本問題.每個樣本可以被視為一條有214個觀測時間點的多變量時間序列信號，每個觀測點有18個觀測變量.

實驗比較了4種單層模型(LSTM[3]，IndRNN[7],SFM-RNN[8],LTRNN-SFM)在該數據集上的性能.由于數據集較小，模型訓練輪數設置為300輪.實驗結果如圖8所示:

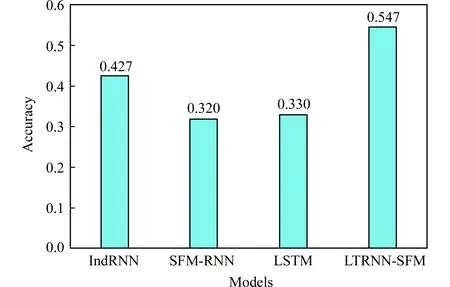
Fig.8 Experimental results for the gesture phase dataset圖8 手勢階段分類數據集實驗結果

由圖8可知，SFM-RNN和LSTM的測試正確率遜于另外2種模型，這證明了LTRNN-SFM的長時記憶能力，也從實驗角度證實了解耦隱藏層神經元、引入ReLU激活函數和權重裁剪后緩解了梯度問題.值得注意的是，LTRNN-SFM比IndRNN的測試正確率高出10%以上，這是由于手勢數據中含有豐富的頻率成分，并且該數據集屬于小樣本問題，LTRNN-SFM既聯合考慮了時域和頻域信息，又能維持長期依賴關系，對數據的表示和擬合能力更強.

4 未來展望

針對現有循環神經網絡在解決時序建模問題時存在的不足,本文提出一種時頻聯合長時循環神經網絡，可以應用于具有長時依賴關系且頻率豐富的時間序列分析任務，包括時間序列預測和時間序列分類.該模型把傳統信號分析手段引入到循環神經網絡，通過將傳統循環神經網絡隱藏層的狀態向量替換為狀態-頻率矩陣，實現對時間序列時域特征模式和頻域特征模式的聯合建模.同時，通過解耦隱藏層神經元、引入非飽和激活函數ReLU和權重裁剪，有效地避免了梯度消失和梯度爆炸問題，使神經網絡模型既可以維持長期記憶，又更加容易訓練深層網絡.實驗結果表明：該模型比目前循環神經網絡模型具有更好性能、更適合時間序列分析.

對于時頻聯合長時循環神經網絡，未來可以從3個方面進行改進：1)如何設計更好的多層模型結構;2)是否可以使模型隱藏層中神經元不是完全獨立而是部分連接;3)如何讓模型有更廣泛的針對性或適用性.這些都是我們未來的研究方向.