EasiFFRA:一種基于鄰域粗糙集的屬性快速約簡算法

王 念 彭政紅 崔 莉

1(中國科學院計算技術研究所 北京 100190)2(中國科學院大學 北京 100190)(wangnian@ict.ac.cn)

在物聯網應用場景中，系統通常需要部署大量感知節點來獲取環境信息.為充分利用每個節點的傳感信息以支持后續精準的識別與預測，實際應用中系統通常會從每個節點的原始信息中提取大量特征，并通過串行融合[1]的方式對數據集進行特征級多源信息融合，形成超級特征(super feature)，并進行后續的機器學習模型訓練和驗證操作.但在每個傳感器的大量特征中，通常包含了與決策任務無關、弱相關或相互冗余的特征.此類特征不但對于決策結果無明顯貢獻，而且會增加計算量，從而降低決策效率，進而影響后續分類或預測操作的性能.若可找出并去除此類特征，則可提高系統實時性并減少所需傳感器的種類及數量.因此在特征工程中，有必要在決策前對原始數據進行降維操作.

目前常用的降維方法包括線性方法、相關性分析法、主成分分析法和基于鄰域粗糙集的特征約簡方法等[2].其中，線性方法無法適用于非線性場景；相關性分析和主成份分析法會造成原屬性集中部分信息丟失；而基于粗糙集的方法能夠在無任何先驗知識(如統計中的先驗概隸屬度等)的情況下，保留數據集的基本知識和分類能力，并消除重復和冗余的特征，是一種有效的特征約簡算法.然而目前已有的基于鄰域粗糙集的特征約簡算法[3-5]中存在較多冗余計算，嚴重限制了算法的執行效率.約簡效率會影響算法的整體實時性，尤其對于在線學習以及數據有較強時效性的場景中，頻繁或定期的模型重構會要求較高的特征約簡速度.針對上述問題，本文提出了一種基于鄰域關系對稱性及決策值過濾策略的特征快速約簡算法(Easi fast Hash feature reduction algorithm,EasiFFRA).

1 相關工作與背景知識

1.1 背景知識

粗糙集理論是Pawlak[6]提出的一種定量分析處理不精確、不一致和不完整信息的方法.目前該理論已被廣泛應用于人工智能、模式識別和數據挖掘等領域[7-10].但作為一種有效的粒度計算模型，粗糙集理論只適用于名義型數據，無法直接應用于現實中廣泛存在的連續型數據.為處理連續性數據，研究人員往往需要對連續型數據進行離散化，但這一轉換不可避免地帶來了信息損失，且計算結果受到了離散化的影響.為解決這一問題，胡清華等人[3]基于拓撲空間球形鄰域提出了鄰域粗糙集(neighborhood rough set,NRS)理論.其核心是使用鄰域近似代替經典粗糙集中的等價關系，以使其既支持離散型數據又支持連續型數據.鄰域粗糙集有效拓展了粗糙集的應用范圍，使其在特征約簡、模式識別等方面有著長足的發展[11-14].

1.2 相關工作

特征約簡是鄰域粗糙集最重要的也是核心內容之一[4,8,15-16].通常，系統的特征相對約簡結果不唯一，人們期望找到一種具有最少特征維度的約簡方法，即最小約簡.但尋找最小約簡已被證明是一種NP難問題[17]，故而研究者們主要致力于用高效的約簡算法找到一個較優的屬性子集[4-5,16,18].胡清華等人[3,5]利用正域與屬性集的單調關系提出了基于前向貪心啟發式搜索策略(fast forward heterogeneous attribute reduction based on neighborhood rough sets,F2HARNRS)算法，該算法從空集開始構建約簡集合，每一次迭代過程都將當前特征集合中具有最大正域值的屬性加入約簡集合，并過濾掉論域中已經屬于正域的樣本.雖然通過去除正域樣本縮小了搜索空間，但整個約簡算法時間復雜度仍為O(m||U|2)，其中m為屬性個數，|U|為樣本總個數，并且算法效率會受到數據分布情況的影響.為解決F2HARNRS算法鄰域計算的時間復雜度過高的問題，Liu等人[4]在文獻[3,5]的基礎上提出了基于散列劃分桶縮小鄰域搜索空間的屬性快速約簡算法(fast Hash attribute reduct algorithm,FHARA).該方法根據給定的鄰域決策系統NDS=〈U,C∪D,V,f〉及距離度量δ，利用散列映射將論域U中的樣本劃分到有限集合B0,B1,…,Bb中.樣本劃分情況如圖1所示：

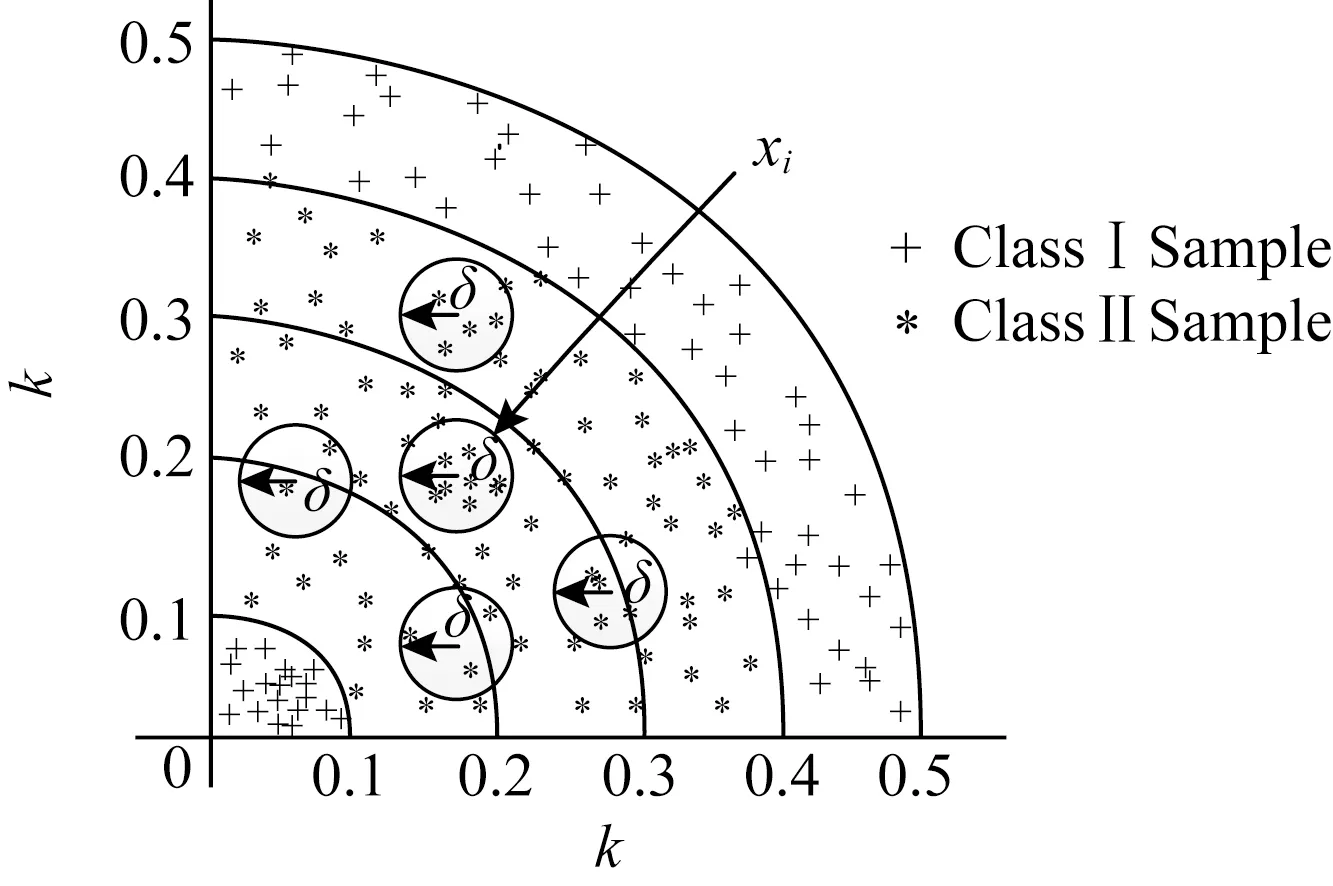
Fig.1 The distribution of the buckets圖1 桶劃分示意圖

映射函數為Bk={xi|xi∈U∧┌f(x0,x1)/δ┐=k}，其中x0是由每個屬性的最小值組成的一個特殊樣本.以k作為散列鍵[4]組成的數據桶的空間分布類似由多個大小不等的球嵌套而成的組合體,散列鍵k為映射后球的半徑.樣本分布在球面與球面之間，B0,B1,…,Bn就是以k作為半徑所得的n個數據桶.經過桶劃分策略進行樣本空間映射后，集合中的每個樣本的鄰域搜索范圍由原來的整個樣本空間減小到相鄰的3個數據桶，與F2HARNRS算法相比，FHARA明顯降低了樣本鄰域的搜索范圍，降低了算法的計算復雜度.

如圖1所示，在計算某個樣本xi的鄰域時，只需考慮xi所在桶以及相鄰2個桶內的樣本.Liu等人[4]提出的散列分桶策略縮小了鄰域樣本存在的可能范圍，使得整個約簡算法時間復雜度下降為O(m|U|2/k)，其中k為桶的個數.然而，分析發現每個桶中依然存在大量不屬于xi鄰域的樣本，這意味著FHARA在計算樣本的鄰域時仍然存在很多冗余計算.以表1中的樣例數據為例，其中a,b,c,d為條件屬性，即特征(feature)；e為決策屬性，即標簽(label).當δ=0.1時，則有x0={0.17,0.11,0.27,0.33}，樣本的桶劃分情況為：B0={x7},B1={x1,x2,x3,x6},B2={x4},B3={x5,x8}.FHARA首先計算B0中樣本x7的鄰域.由桶劃分機制可知，在計算B0中樣本的鄰域時只需遍歷B1即可.記xi與xj之間的距離為D(xi,xj)，則D(x7,x1)=0.152，D(x7,x2)=0.148，D(x7,x3)=0.19，D(x7,x6)=0.093.當計算出x7與x1的距離D(x7,x1)大于鄰域半徑δ時，系統可推斷x1不在鄰域范圍內.同理，x2,x3也不在鄰域范圍內.計算x7與x6的距離，發現D(x7,x6)小于鄰域半徑，但兩者擁有不同的決策值，可知x7為邊界區樣本；至此，B0中樣本的鄰域計算完畢.計算B1中樣本的鄰域，需要遍歷B0∪B1∪B2桶.首先計算樣本x1與x7的距離D(x1,x7).而D(x1,x7)與D(x7,x1)等價，故而沒有必要重復計算.可以看出，FHARA的鄰域計算過程中存在冗余計算.

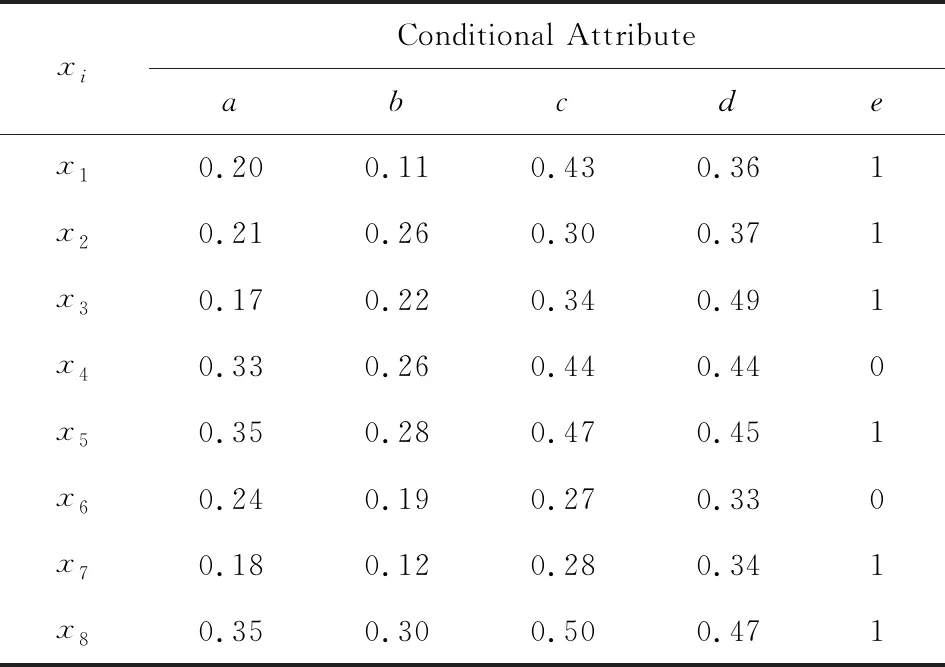
Table 1 An Example Dataset表1 樣例數據

蔣云良等人[19]在文獻[3-5]的基礎上，采用迭代的方式求解樣本鄰域，即在每次迭代過程中只搜索Bk和Bk+1兩個桶，避免了FHARA中相鄰桶內樣本鄰域關系的重復計算問題.但是該算法須計算Bk與Bk+1之間的完整鄰域關系，以便在下一次迭代過程中避免搜索Bk-1桶(即當前迭代中的Bk桶).故而當鄰域樣本分布在相鄰的多個桶中時，該算法的鄰域計算量較大.

文獻[3,5,19]均可利用鄰域粗糙集理論實現特征約簡.其中文獻[3,5]初步建立了特征約簡的思路，即迭代貪心搜索并保留具有最大正域值的屬性；文獻[4]發現貪心搜索中正域計算時的鄰域搜索空間的遍歷具有盲目性，于是針對此提出了基于散列劃分桶的方法.該方法可以縮小鄰域搜索空間并避免部分冗余計算；文獻[19]也基于文獻[3,5]的算法框架，約束了正域計算過程中桶搜索的范圍，避免相鄰桶內樣本鄰域關系的重復計算問題，從而進一步提高了鄰域粗糙集特征約簡的效率.但現有的特征約簡算法中仍存在冗余計算.

針對當前已有方法中存在的鄰域冗余計算問題和鄰域計算量過大的問題，本文提出基于鄰域對稱性及決策值過濾策略的屬性快速約簡算法(EasiFFRA)，并在太湖實際采集的水質監測數據集合，以及多個UCI(University of California Irvine)國際標準數據集上進行實驗，以驗證本方法的有效性.本文的主要貢獻體現在3個方面：

1)通過散列表存儲鄰域計算過程中被判定為邊界區的樣本，減少了鄰域計算過程中的冗余計算量；

2)采用優先搜索樣本所在桶的策略，提前發現鄰域樣本，從而加速正域的計算；

3)采用決策值過濾策略，減少了鄰域距離的計算次數，從而大幅降低算法的計算量；

對比實驗表明：EasiFFRA在同等約束條件下有較大優勢，可以在保持約簡結果的情況下加快特征約簡的速度.

2 鄰域粗糙集屬性約簡機制

在已有的基于鄰域粗糙集的特征約簡步驟中，算法通常需要遍歷并保留能夠引起最大正域樣本增量的特征，直到增加其他特征也無法引起正域集合的擴大，算法停止.在該類約簡過程中，算法需要對所有未保留的特征進行遍歷，并計算每種組合下的正域樣本集合.此過程是算法中計算量最大的步驟，存在計算冗余.本節介紹在文獻[4]的基礎上所提出的基于鄰域對稱性和決策值過濾策略的EasiFFRA特征快速約簡算法.

2.1 基于鄰域對稱性的約簡機制

鄰域具有對稱性[3]，該性質可用于避免大量現有工作中的冗余正域計算操作即在度量空間和δ鄰域中，有：

δ(xi)≠?,?xi∈δ(xi),

(1)

xj∈δ(xi)?xi∈δ(xj),

(2)

(3)

也就是說，如果xi是xj的鄰域樣本，那么xj也是xi的鄰域樣本，如圖2所示:

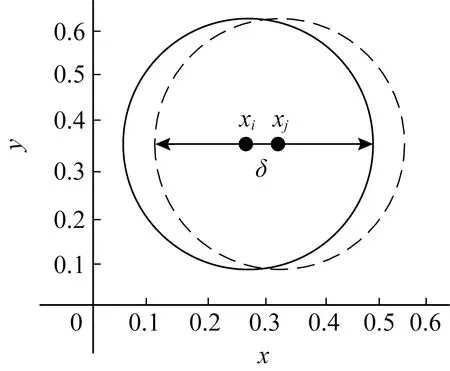
Fig.2 Neighborhood symmetry圖2 鄰域對稱性示意圖

在鄰域粗糙集理論中，數據集合可以分為3個區間，即A類樣本正域、B類樣本正域和邊界區.其中正域樣本是在數據集中可以根據其自身特征分布明確分類的樣本；而邊界區的樣本則是無法十分明確歸類的樣本，即存在一定的混淆.在判斷某樣本xi是否為正域元素的過程中，需要遍歷xi鄰域范圍內的所有樣本的標簽值.若在xi鄰域范圍內存在與其標簽值不同的樣本，則xi為邊界區樣本；若xi鄰域內所有的樣本均與其標簽值相同，則xi為正域樣本.

不同類別樣本正域和邊界區中樣本的并集即為整個數據集.邊界區數據集合和正域中數據集合不相交.

根據正域的定義及其計算規則，在同一屬性子集條件下計算樣本xi的鄰域時，如果xj在xi的鄰域范圍之內，且xj與xi的決策屬性不同(不屬于同一類別)，則xi不可能屬于正域集合.同理，由于對稱性xj也不可能屬于正域集合.根據這一特性，通過一個散列表Hs來存儲尚未計算過鄰域但已經判定為邊界區的樣本子集.比如若判定xj導致xi為邊界區樣本，則將xj存入散列表Hs，在后序判斷xj是否為正域樣本時，將首先檢索散列表Hs中是否存在xj的記錄，如果存在則無需檢索任何桶中的樣本，可直接將xj判別為邊界區樣本，從而避免了大量冗余的鄰域計算.

由散列分桶映射函數可知，散列桶劃分策略使得距離相近的樣本以更大概率被劃分到同一個桶中，即樣本xi(xi∈Bk)的鄰域樣本出現Bk中的概率大于出現在Bk+1和Bk-1桶的概率.這也意味著Bk桶內出現由xi導致的邊界區樣本的概率大于Bk+1，Bk-1中出現由xi導致的邊界區樣本的概率.所以在改進算法中，優先檢索Bk桶.又因為Bk-1中的非鄰域樣本在上一輪迭代過程中已經存儲在散列表Hs中，無需再次檢驗存儲，所以可以在檢索Bk后直接檢索Bk+1桶.基于上述桶檢索順序，并結合鄰域的對稱性，可以盡早的發現盡可能多的邊界區樣本，減少不必要的檢索計算.在后續的實驗部分中將對其進行進一步的論述與驗證.

2.2 基于決策值過濾策略的約簡機制

在已有鄰域粗糙集特征約簡算法的正域計算步驟中，當判斷樣本xi是否處于正域時，需遍歷樣本集中所有其他數據xj，并計算xi與所有xj之間的距離，而不論xj和xi的決策屬性類別是否相同、是否處于同一個鄰域內.這種樸素的計算方法中存在若干冗余計算：

在樣本xi正域的求解過程中，若其δ鄰域中存在一個決策屬性不同的樣本，則xi將被判別為邊界區樣本.只有當xi的δ鄰域中所有樣本都與其決策屬性相同時，xi才會被劃分為正域樣本.故而可以將樸素的遍歷過程簡化為僅關注xi的δ正域內是否存在異類決策屬性的樣本即可.

在本文提出的算法中，僅遍歷與樣本xi決策屬性類別不同的樣本子集，計算并考察該樣本子集中各樣本點xj與xi間的距離D(xi,xj)，此時有2種情況：

1)若D(xi,xj)>δ，則xj不會對xi的正域判別產生影響；

2)若D(xi,xj)<δ，則由于xj的影響，xi將無法被歸類為正域元素，并被劃分入邊界區.

綜上，在判斷xi是否為正域樣本時，只需考慮與xi決策屬性不同的樣本子集.該集合中與xi決策屬性相同的樣本不會對xi的正域屬性判斷產生影響，可以直接忽略，此方法即為決策值過濾策略.

例如在表1的樣例數據中，可以首先比較x7與x1,x2,x3的決策屬性，發現決策屬性均相等，便可直接省去x7與x1,x2,x3間的距離計算.雖然決策值過濾策略并未降低算法的時間復雜度，但是可以減少大量樣本間的距離計算，使得整個約簡算法的計算開銷大幅下降，正域的求解效率也就得以提高.

實驗表明:對于決策屬性取值情況較少的數據集，尤其是二分類的情況，通過決策值過濾策略帶來的計算效率提升十分明顯.

2.3 屬性約簡改進算法

結合鄰域對稱性和決策值過濾機制，下面給出正域求解算法的偽碼，如算法1所示.

算法1.基于對稱及決策過濾的快速約簡算法.

輸入：U,P,D,δ；

輸出：F={F1,F2,…,F|U|}.

①Fi←0,1,…,|U|；

② for eachxi∈Udo

③ Hash(P(xi),Bk)；

④ end for

⑤ for eachxi∈Udo

⑥flag←0；

⑦ ifxi∈Non_Posthen

⑧flag←1；

⑨ else

⑩ for eachxi∈Bk∪Bk+1do

其中，由于Bk-1桶的處理與Bk∪Bk+1類似，唯一區別是無需將Bk-1桶的邊界區樣本存入散列表Hs(因為這些邊界區樣本在上一輪迭代過程中已經存入散列表Hs)，故而其操作過程在算法中省略.

算法1可判斷樣本是否為正域樣本，其流程如圖3所示，其中以xi,xj的單次比較為例.下面結合流程圖對算法1進行闡述.

算法1首先判斷xi是否存在于記錄邊界區樣本的散列表Hs中，如果存在則說明xi在前面的迭代過程中曾導致其他樣本成為邊界區樣本.根據鄰域對稱性，xi也不是正域樣本，故而被存入散列表Hs中.此時可直接判斷xi為邊界區樣本，并將xi的標志位flag設置為1.其中標志位為記錄該樣本是否為邊界區樣本的標志位.

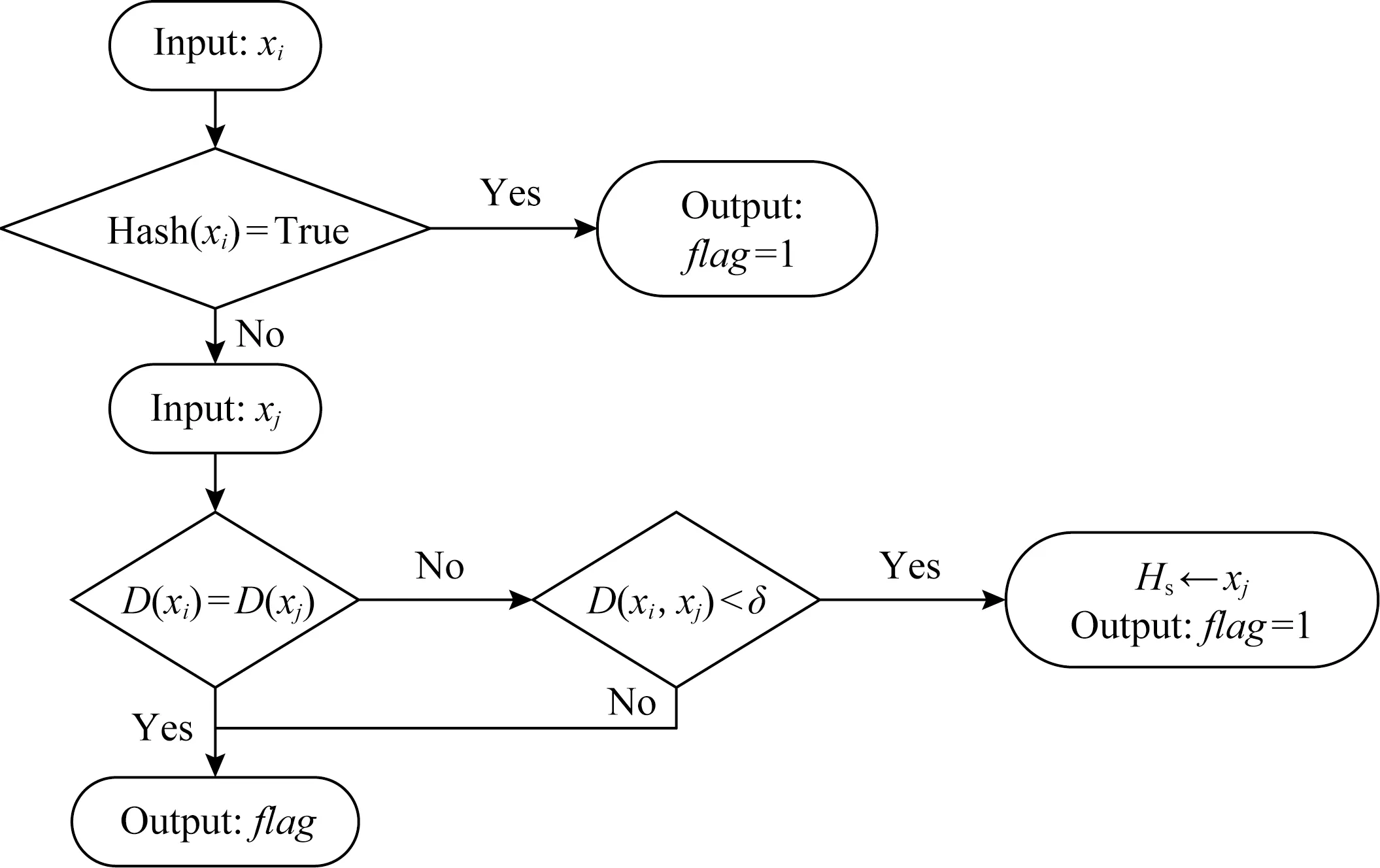
Fig.3 Positive region computation algorithm圖3 正域的計算流程圖

如果xi不在散列表Hs中則需要檢索鄰域空間的樣本.假設檢索到樣本xj，首先判斷xi和xj的決策值是否相等.如果相等則根據決策值過濾機制可無需繼續計算xi和xj之間的距離，可以直接轉向其他樣本的檢索；如果決策值不相等則繼續計算鄰域距離D(xi,xj)；

如果D(xi,xj)>δ，則說明xi不是xj的鄰域樣本，它對xi是否為正域樣本的判斷無影響，所以無需修改標志位；如果D(xi,xj)≤δ則說明xi為邊界區樣本，則將標志位置為1，根據鄰域對稱性可知，xj也為邊界區樣本，需將xj存入散列表Hs.

3 實驗分析

為了驗證本文提出的EasiFFRA算法的正確性與約簡的高效性，本節將其與現有方法中特征約簡時間效率最高的FHARA方法進行對比實驗.實驗內容包括算法的正確性驗證以及算法的高效性驗證.實驗數據包括本研究組實際部署與監測的水質監測系統藻類數據集blue green algae[20]，以及UCI公開數據集中的12組樣本.實驗中使用的數據集名稱、樣本數量、特征維度和決策屬性數量信息如表2所示.

實驗中，所有算法均選取歐氏距離作為正域計算度量函數，測試運行在相同的軟件和硬件環境下CPU為Intel Core i5-4590 CPU@3.30 GHz;RAM為8.00 GB;Windows 7 OS;python 2.7.10.為保證數據的有效性和結果的可重復性，結論中的約簡結果以及特征約簡速度數據均為10次相同環境下運行結果的平均值.

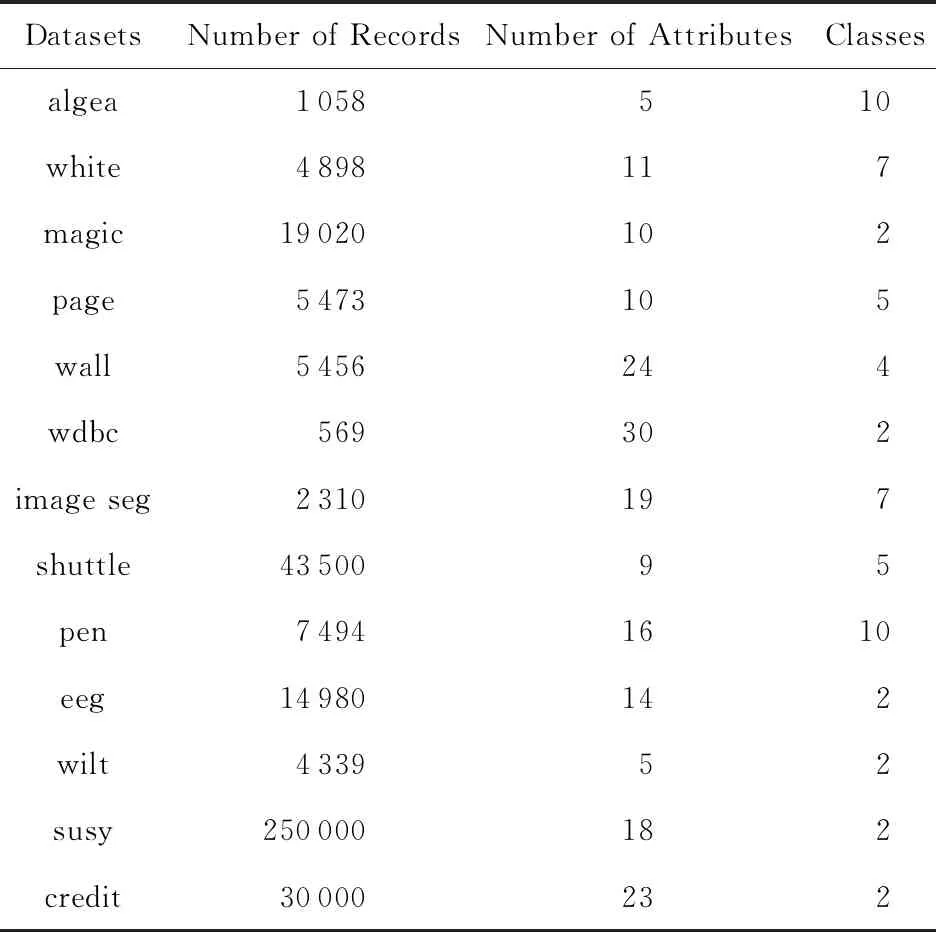
Table 2 Datasets Used in Experiments表2 實驗數據集

3.1 算法正確性驗證

為驗證EasiFFRA算法的正確性，實驗同時在algea以及12個UCI數據集上同時執行FHARA算法以及EasiFFRA算法，并比較它們的約簡結果.約簡結果如表3所示.

從表3可以看到，EasiFFRA和FHARA在所有數據集上的約簡結果均相同，又因為文獻[4]中FHARA的正確性驗證、可驗證本文提出的EasiFFRA算法約簡結果的一致性與正確性.為進一步驗證EasiFFRA約簡結果的正確性，實驗同時比較經過EasiFFRA約簡、經過常用的隨機森林特征約簡和未經任何約簡的數據集的5折交叉分類精度，結果如圖4所示.其中使用SVM作為分類器.

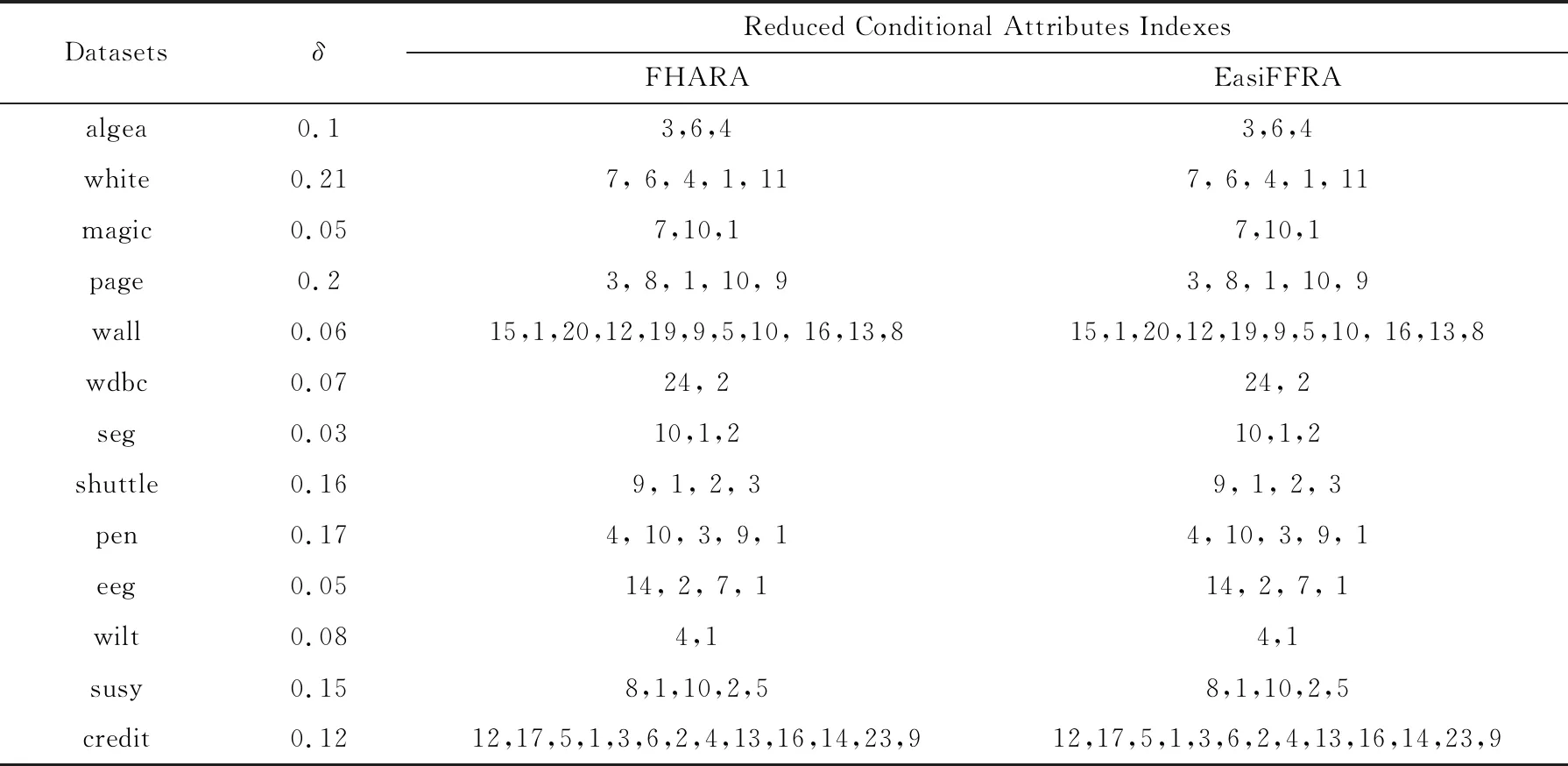
Table 3 Attributes Selected by Two Reduct Algorithms表3 2種算法約簡結果

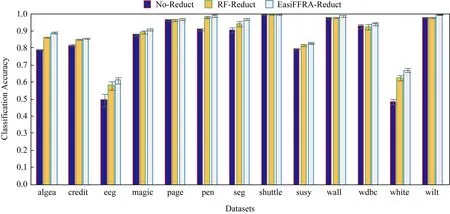
Fig.4 Classification accuracy of SVM in several datasets with EasiFFRA reduction,no-reduction and random forest reduction圖4 EasiFFRA與無約簡及隨機森林約簡后各數據集精度對比

從圖4可以看到，建立在經過特征約簡后的數據集上的分類器的識別精度優于未經約簡的原始數據集的精度.而在約簡算法中，經過EasiFFRA處理的分類器精度普遍高于傳統的隨機森林約簡算法的結果.這也從另一方面驗證了本文提出的EasiFFRA特征約簡算法的正確性.

3.2 算法約簡效率對比實驗

為驗證EasiFFRA的特征約簡的高效性，實驗分別統計EasiFFRA以及對比方法執行過程中的樣本間距離計算次數、整體算法運行時間以及算法運行時間隨樣本數量增加而延長的計算耗時.

1)計算EasiFFRA在不同桶搜索順序下樣本距離的計算總量，以及FHARA在相同數據集下的樣本間距離計算次數.如表4所示.

表4表頭中EasiFFRA后跟隨的3位數字代表EasiFFRA算法在不同桶搜索順序下的算法，如012代表依次搜索Bk-1，Bk，Bk+1桶.從表4可知，在桶搜索順序的選擇中，優先搜索Bk時的樣本距離計算次數與開銷最少；對比EasiFFRA與FHARA的距離計算次數可知，EasiFFRA算法在6種桶搜索順序下的距離計算開銷均少于FHARA算法.特別在wilt，magic，credit，shuttle等決策屬性種類較少的數據集上的效率提升最多，在seg，pen等決策值種類較多的數據集上計算量也有著明顯的降低.以EasiFFRA102的桶搜索順序為例，EasiFFRA在pen上的距離計算次數小于FHARA距離計算次數的1/3，在seg上的計算次數小于FHARA計算次數的 1/4，在algea上的距離計算次數不到 FHARA 距離計算次數的 1/19.

2)計算EasiFFRA 在相同條件下的算法執行時間.為驗證算法的普適性和有效性，按照鄰域半徑δ將實驗分為0.08和0.15這2組.實驗結果如圖5所示.

為直觀展示 EasiFFRA 的約簡高效性，實驗統計了2種方法的約簡計算時間(單位為s)，如表5所示.

從表5看到，相對于現有的FHARA方法，不論在δ=0.08還是δ=0.15的情況下，本文提出的EasiFFRA算法在12個驗證數據集上均具有更高的約簡效率，且對于決策值種類較少的數據集提升更為明顯.EasiFFRA在12個數據集上的平均約簡時間僅為對比方法FHARA的24.45%.此外，在algae數據集中樣本不平衡問題十分嚴重，其中決策值為0的樣本占整體數據量的92.34%，其他9個決策值的樣本共占整體數據量的7.66%，可見EasiFFRA在該類決策值種類多且分布不平衡的情況下也能夠達到很好的約簡性能，驗證了其良好的適用性.

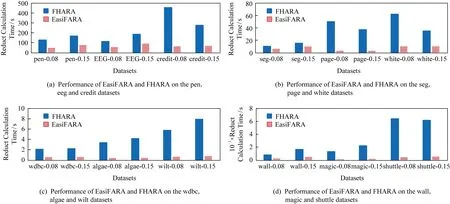
Fig.5 Reduct calculation time cost of FHARA and EasiFFRA on 12 UCI datasets with δ equals 0.08 and 0.15圖5 δ=0.08和δ=0.15 時，EasiFARA和FHARA算法在12個UCI數據集上的約簡時間

Table 5 Ratio of Reduct Calculation Time Cost of FHARA and EasiFFRA表5 EasiFFRA與FHARA約簡時間比

3)實驗在保持鄰域半徑不變的情況下，對比EasiFFRA和FHARA算法在隨樣本量增加而延長的算法耗時.在本實驗中，除了用到的12個數據集外，實驗還從UCI數據集中提取了含有250 000個樣本的susy數據子集來驗證EasiFFRA在大數據集下的性能表現.實驗結果如圖6和表6～9所示.

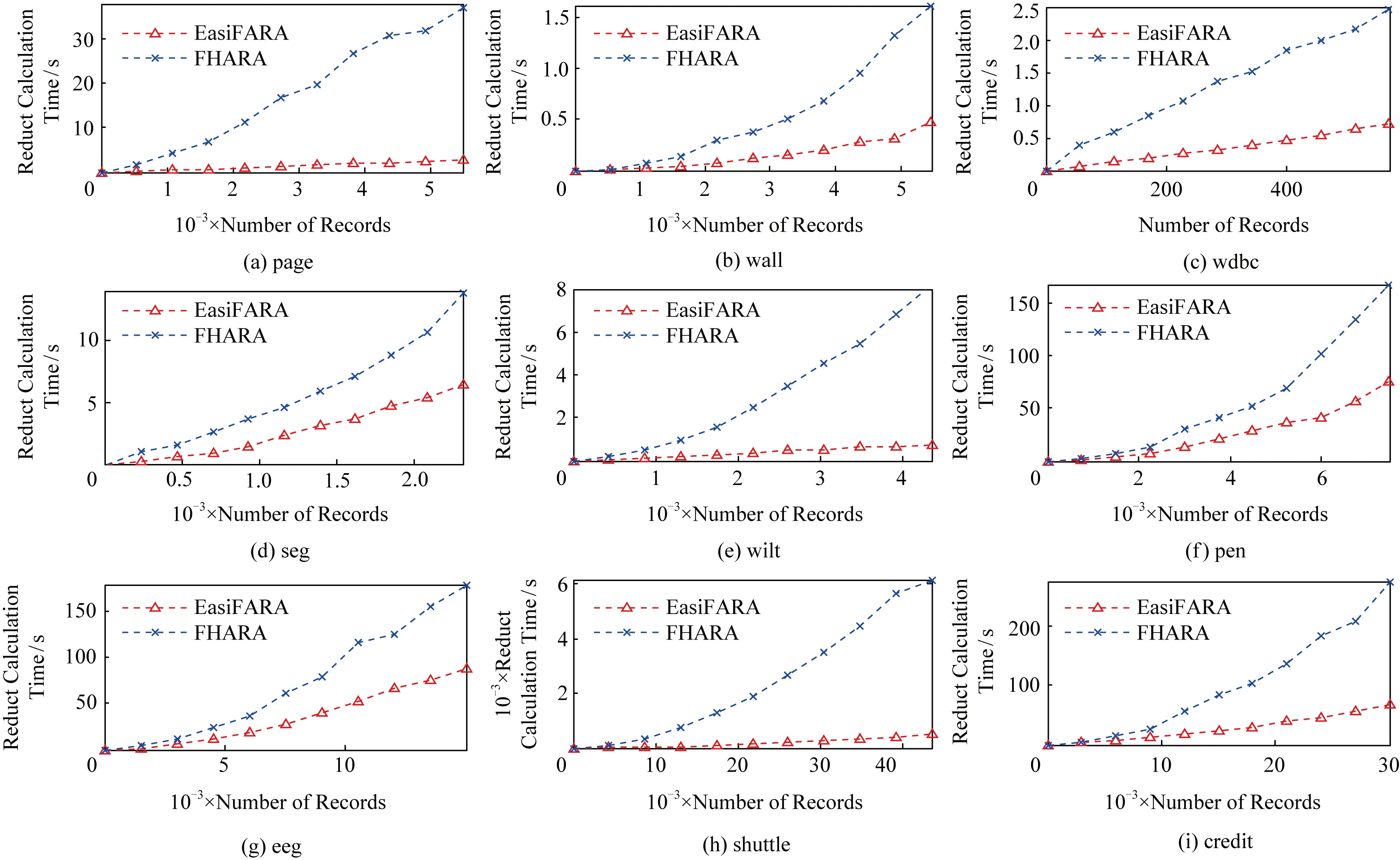
Fig.6 Calculation time cost of EasiFFRA and FHARA on 9 datasets with increasing sample size圖6 FHARA和EasiFFRA在9個數據集上隨著樣本數量的增加所消耗的時間

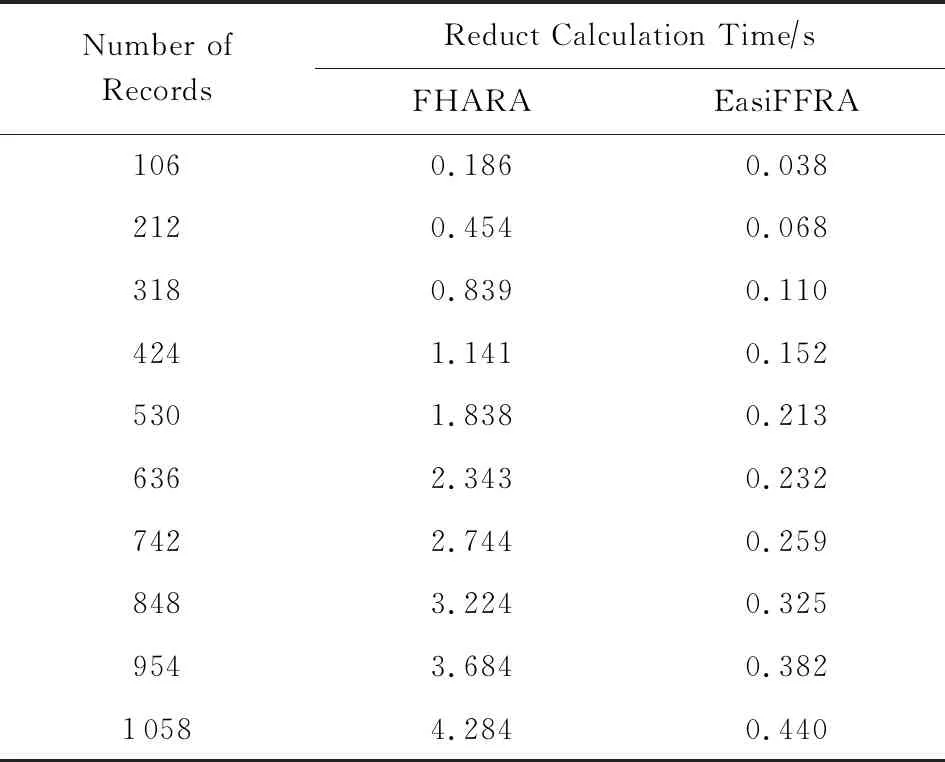
Table 6 Calculation Time Cost of EasiFFRA and FHARA on algae表6 EasiFFRA和FHARA在algae數據集上的約簡時間

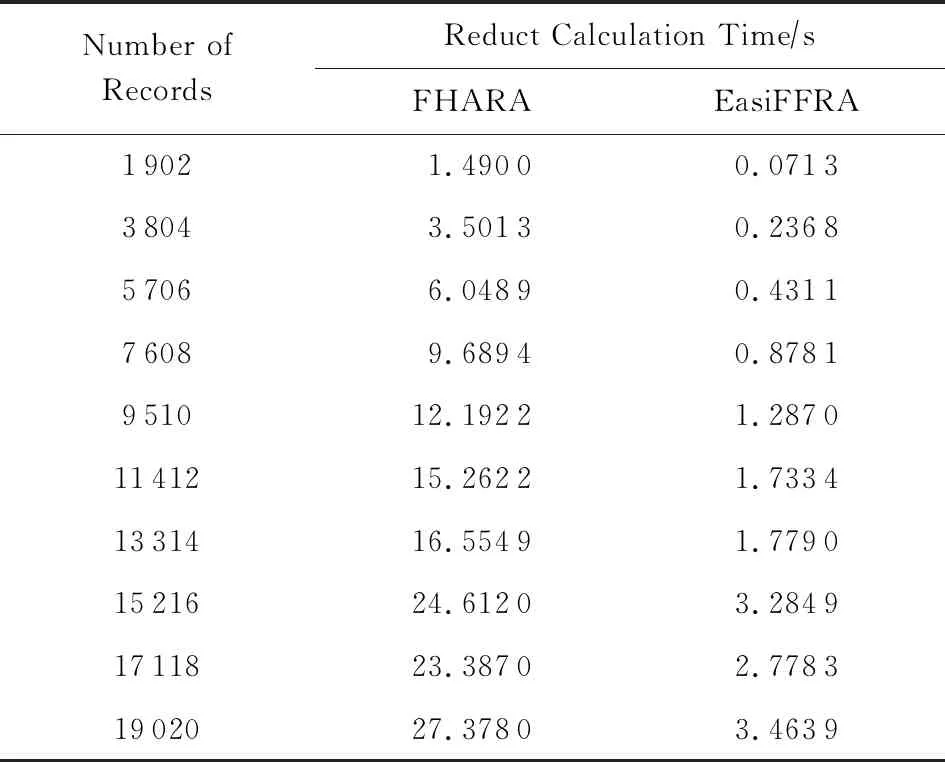
Table 7 Calculation Time Cost of EasiFFRA and FHARA on magic表7 EasiFFRA和FHARA在magic數據集上的約簡時間

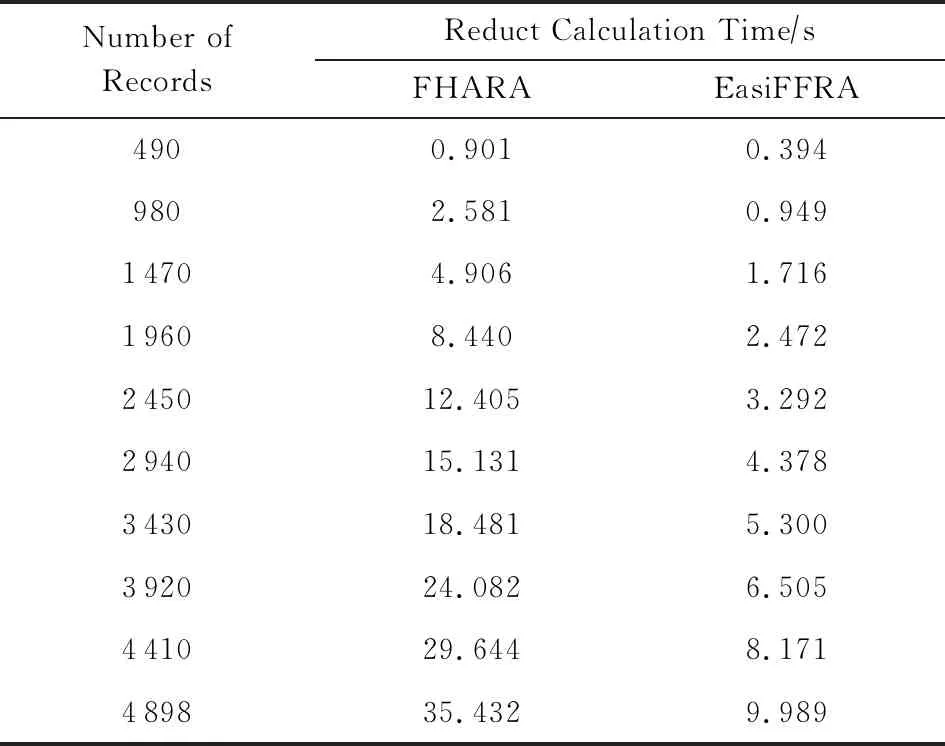
Table 8 Calculation Time Cost of EasiFFRA and FHARA on white表8 EasiFFRA和FHARA在white數據集上的約簡時間

從實驗結果中可以看到，隨著樣本量的增加，EasiFFRA在這13個數據集上的約簡效率均優于FHARA.尤其在shuttle,susy等決策值種類較少且數據量大的場景下，EasiFFRA的約簡耗時明顯低于FHARA.上述現象說明EasiFFRA算法能夠更好地適用于大數據應用場景.

4 結 論

物聯網場景中的大量感知數據的特征具有高維、冗余、非線性等特點.冗余特征和無關特征會導致分類模型準確率下降，也會造成計算資源浪費，因此有必要對數據集進行降維預處理.相對于其他降維算法，鄰域粗糙集特征約簡算法能夠在保持數據可分性的前提下刪除無關、弱相關和冗余特征，具有很大的應用優勢，但其較大的計算復雜性成為算法實際部署的瓶頸.本文針對鄰域計算時間復雜度過高、計算量過大的問題，提出了基于鄰域關系對稱性及決策值過濾策略的特征約簡算法EasiFFRA.該算法優先檢索鄰域樣本分布相對集中的相鄰桶Bk，采用散列表存儲當前屬性子集條件下不可能成為正域樣本的方法，縮小鄰域檢索范圍；并通過決策值過濾策略過濾掉與當前樣本具有相同決策值的冗余樣本，減少了鄰域計算時的距離計算次數，從而降低算法的計算量.對比實驗表明EasiFFRA避免了大量冗余計算，算法效率明顯優于對比方法，能更好地適應復雜的物聯網數據分析場景.