與Euler函數φ(n)有關的一個四元不定方程的解

張四保，楊燕妮，姜蓮霞，席小忠

(1.喀什大學 數學與統計學院, 新疆 喀什 844008；2.宜春學院 數學與計算機科學學院, 江西 宜春 336000)

Euler函數φ(n)是數論中的一個重要函數，與Euler函數φ(n)有關的不定方程的研究內容豐富，文獻頗多，如文獻[1-3]都討論了與Euler函數φ(n)有關的不定方程的整數解問題。許多文獻對于以下形式的方程

φ(x1x2…xn)=k(φ(x1)+φ(x2)+…+φ(xn))

(1)

也進行了豐富的研究。如文獻[4]討論了當n=2，k=2時方程(1)的解問題；文獻[5]討論了當n=2，k=11時方程(1)的解問題；文獻[6]討論了當n=2，k=4,6時方程(1)的解問題；文獻[7]討論了當n=2，k=4時方程(1)的解問題；文獻[8]討論了當n=2，k=7時方程(1)的解問題；文獻[9]討論了當n=3，k=2時方程(1)的解問題；文獻[10]討論了當n=3，k=5時方程(1)的解問題；文獻[11]討論了當n=3，k=6時方程(1)的解問題；文獻[12]討論了當n=4，k=2時方程(1)的解問題。本文將討論方程(1)中當n=4，k=4時所對應的方程的解問題，即討論了方程

φ(xyzw)=4(φ(x)+φ(y)+φ(z)+φ(w))

(2)

的解問題,利用初等方法給出了其滿足x≤y≤z≤w的整數解，再由對稱性確定其全部的整數解。

1 定理及其證明

定理1數論函數方程(2)滿足x≤y≤z≤w的整數解為(x,y,z,w)= (1,1,5,35)，(1,1,5,45)，(1,1,5,70)，(1,1,5,90)，(1,1,6,24)，(1,1,6,30)，(1,1,7,17)，(1,1,7,32)，(1,1,7,34)，(1,1,7,40)，(1,1,7,48)，(1,1,7,60)，(1,1,8,14)，(1,1,8,18)，(1,1,9,17)，(1,1,9,32)，(1,1,9,34)，(1,1,9,40)，(1,1,10,10)，(1,1,10,14)，(1,1,10,18)，(1,1,10,35)，(1,1,10,45)，(1,1,11,15)，(1,1,11,16)，(1,1,11,20)，(1,1,11,24)，(1,1,11,30)，(1,1,12,14)，(1,1,12,21)，(1,1,14,17)，(1,1,15,22)，(1,1,17,18)，(1,2,3,24)，(1,2,3,30)，(1,2,4,8)，(1,2,4,10)，(1,2,4,12)，(1,2,5,10)，(1,2,5,14)，(1,2,5,18)，(1,2,5,35)，(1,2,5,45)，(1,2,6,6)，(1,2,6,8)，(1,2,6,10)，(1,2,6,15)，(1,2,7,8)，(1,2,7,10)，(1,2,7,12)，(1,2,7,17)，(1,2,8,9)，(1,2,9,10)，(1,2,9,17)，(1,2,11,15)，(1,3,3,11)，(1,3,3,12)，(1,3,3,22)，(1,3,6,11)，(2,2,3,6)，(2,2,3,8)，(2,2,3,10)，(2,2,3,15)，(2,2,4,5)，(2,2,5,6)，(2,2,5,5)，(2,2,5,7)，(2,2,5,9)，(2,3,3,11)。

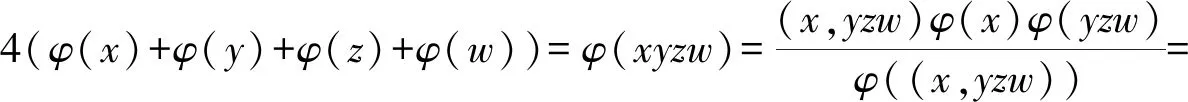
(3)

由于n≥φ(n)，則由式(3)有

4[φ(x)+φ(y)+φ(z)+φ(w)]≥φ(x)φ(y)φ(z)φ(w)

(4)

則

φ(x)[φ(y)φ(z)φ(w)-4]≤4[φ(y)+φ(z)+φ(w)]

(5)

由于當n≥3時，φ(n)為偶數，現可對φ(y)φ(z)φ(w)的值分如下2種情況討論：

情況1φ(y)φ(z)φ(w)≤4，此時φ(y)φ(z)φ(w)=1,2,4。

情況1.1當φ(y)φ(z)φ(w)=1，此時φ(y)=φ(z)=φ(w)=1，則y=z=w=1,2，此時方程(2)無解。

情況1.2當φ(y)φ(z)φ(w)=2，此時φ(y)=φ(z)=1，φ(w)=2或φ(y)=φ(w)=1，φ(z)=2或φ(y)=2，φ(z)=φ(w)=1。由于對稱性，不妨就φ(y)=φ(z)=1，φ(w)=2的情況討論。此時有y=z=1,2，w=3,4,6，則可得此時方程(2)有滿足y≤z≤w的整數解(x,y,z,w)=(24,1,1,6)，(30,1,1,6)，(24,1,2,3)，(30,1,2,3)，(10,1,2,4)，(10,1,2,6)，(15,1,2,6)，(8,1,2,6)，(6,1,2,6)，(10,2,2,3)，(15,2,2,3)，(8,2,2,3)，(6,2,2,3)，(5,2,2,4)，(5,2,2,6)，(3,2,2,6)。

情況1.3當φ(y)φ(z)φ(w)=4。此時φ(y)=φ(z)=1，φ(w)=4或φ(y)=φ(w)=1，φ(z)=4或φ(y)=4，φ(z)=φ(w)=1或φ(y)=1，φ(z)=φ(w)=2或φ(z)=1，φ(x)=φ(w)=2或φ(w)=1，φ(y)=φ(z)=2。不妨就φ(y)=φ(z)=1，φ(w)=4與φ(y)=1，φ(z)=φ(w)=2情況討論。

當φ(y)=φ(z)=1，φ(w)=4時，y=z=1,2，w=5,8,10,12，則可得此時方程(2)有滿足y≤z≤w的整數解(x,y,z,w)=(35,1,1,5)，(45,1,1,5)，(70,1,1,5)，(90,1,1,5)，(14,1,1,8)，(18,1,1,8)，(14,1,1,10)，(18,1,1,10)，(35,1,1,10)，(45,1,1,10)，(10,1,1,10)，(14,1,1,12)，(21,1,1,12)，(35,1,2,5)，(45,1,2,5)，(10,1,2,5)，(7,1,2,8)，(9,1,2,8)，(6,1,2,8)，(7,1,2,10)，(9,1,2,10)，(6,1,2,10)，(4,1,2,10)，(5,1,2,10)，(7,1,2,12)，(4,1,2,12)，(7,2,2,5)，(9,2,2,5)，(6,2,2,5)，(4,2,2,5)，(5,2,2,5)，(3,2,2,8)，(3,2,2,10)。

當φ(y)=1，φ(z)=φ(w)=2時，y=1,2，z=w=3,4,6，則可得此時方程(2)有滿足y≤z≤w整數解(x,y,z,w)=(11,1,3,3)，(22,1,3,3)，(12,1,3,3)，(11,1,3,6)，(2,1,6,6)，(11,2,3,3)，(2,2,3,6)。

情況2φ(y)φ(z)φ(w)≥6。因(φ(y)-1)(φ(z)-1)(φ(w)-1)≥0，則

φ(y)φ(z)φ(w)-1≥φ(y)φ(z)+φ(y)φ(w)+φ(z)φ(w)-(φ(y)+φ(z)+φ(w))

(6)

再因φ(y)φ(z)≥φ(y)+φ(z)-1，φ(y)φ(w)≥φ(y)+φ(w)-1，φ(z)φ(w)≥φ(z)+φ(w)-1，則由式(6)有

φ(y)φ(z)φ(w)+2≥φ(y)+φ(z)+φ(w)

(7)

結合φ(y)φ(z)φ(w)≥8與式(5)、(7)有

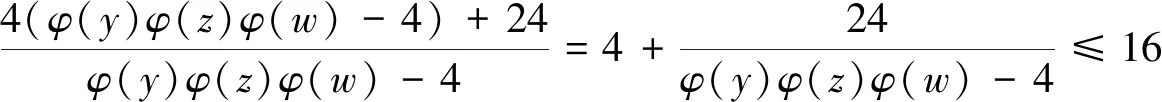
由于14是非Euler商數，因此φ(x)=1,2,4,6,8,10,12,16。

情況2.1φ(x)=16

此時結合式(4)與(7)有12φ(y)φ(z)φ(w)≤72，即φ(y)φ(z)φ(w)≤6，則有φ(y)φ(z)φ(w)=6。則有φ(y)=φ(z)=1，φ(w)=6或φ(y)=φ(w)=1，φ(z)=6或φ(y)=6，φ(z)=φ(w)=1。由于對稱性，不妨就φ(y)=φ(z)=1，φ(w)=6的情況討論。此時y=z=1,2，w=7,9,14,18，則可得此時方程(2)有滿足y≤z≤w整數解(x,y,z,w)=(17,1,1,7)，(32,1,1,7)，(34,1,1,7)，(40,1,1,7)，(48,1,1,7)，(60,1,1,7)，(17,1,1,9)，(32,1,1,9)，(34,1,1,9)，(40,1,1,9)，(17,1,1,14)，(17,1,2,7)，(17,1,1,18)，(17,1,2,9)。

情況2.2φ(x)=12

此時結合(4)與(7)有8φ(y)φ(z)φ(w)≤56，即φ(y)φ(z)φ(w)≤7，結合φ(y)φ(z)φ(w)≥6可得φ(y)φ(z)φ(w)=6。由方程(2)有Pφ(x)=φ(xyzw)=4φ(x)+32，即有(P-4)φ(x)=32，而此時φ(x)=12，12?32，則此時方程(2)無解，符號?表示不整除。

情況2.3φ(x)=10

此時結合式(4)與(7)有6φ(y)φ(z)φ(w)≤48，即φ(y)φ(z)φ(w)≤8，結合φ(y)φ(z)φ(w)≥6可得φ(y)φ(z)φ(w)=6,8。

當φ(y)φ(z)φ(w)=6時，類似情況2.2的說明，可得此時方程(2)無解。

當φ(y)φ(z)φ(w)=8時，有φ(y)=φ(z)=1，φ(w)=8或φ(y)=φ(w)=1，φ(z)=8或φ(y)=8，φ(z)=φ(w)=1或φ(y)=1，φ(z)=2，φ(w)=4或φ(y)=1，φ(z)=4，φ(z)=2或φ(y)=2，φ(z)=1，φ(w)=4或φ(y)=2，φ(z)=4，φ(w)=1或φ(y)=4，φ(z)=1，φ(w)=2或φ(y)=4，φ(z)=2，φ(w)=1。由于對稱性，不妨就φ(y)=φ(z)=1，φ(w)=8與φ(y)=1，φ(z)=2，φ(w)=4進行討論。

當φ(y)=φ(z)=1，φ(w)=8時，此時y=z=1,2，w=15,16,20,24,30，則可得此時方程(0.2)有滿足y≤z≤w整數解(x,y,z,w)=(11,1,1,15)，(22,1,1,15)，(11,1,1,16)， (11,1,1,20)，(11,1,1,24)，(11,1,1,30)，(11,1,2,15)。

當φ(y)=1，φ(z)=2，φ(w)=4時，此時由方程(2)有Pφ(x)=4φ(x)+28，即有(P-4)φ(x)=28，而此時φ(x)=10，10?28，則此時方程(2)無解。

情況2.4φ(x)=8

此時結合式(4)與(7)有4φ(y)φ(z)φ(w)≤40，即φ(y)φ(z)φ(w)≤10，結合φ(y)φ(z)φ(w)≥6可得φ(y)φ(z)φ(w)=6,8,10。

當φ(y)φ(z)φ(w)=6時，結合情況2.1中情況的討論與φ(x)=8，可得此時方程(2)無解。

當φ(y)φ(z)φ(w)=8時，結合情況2.3中情況的討論與φ(x)=8，可得此時方程(2)無解。

當φ(y)φ(z)φ(w)=10時，有φ(y)=φ(z)=1，φ(w)=10或φ(y)=φ(w)=1，φ(z)=10或φ(y)=10，φ(z)=φ(w)=1。由于對稱性，不妨就φ(y)=φ(z)=1，φ(w)=10進行討論。此時y=z=1,2，w=11,22，則可得此時方程(2)有滿足y≤z≤w的整數解(x,y,z,w)=(15,1,1,11)，(16,1,1,11)，(20,1,1,11)，(24,1,1,11)，(30,1,1,11)，(15,1,1,22)，(15,1,2,11)。

情況2.5φ(x)=6

此時結合式(4)與(7)有2φ(y)φ(z)φ(w)≤32，即φ(y)φ(z)φ(w)≤16，結合φ(y)φ(z)φ(w)≥6可得φ(y)φ(z)φ(w)=6,8,10,12,16。

當φ(y)φ(z)φ(w)=6時，結合情況2.1中情況的討論與φ(x)=6，可得此時方程(2)無解。

當φ(y)φ(z)φ(w)=8時，結合情況2.3中情況的討論與φ(x)=6，可得此時方程(2)無解。

當φ(y)φ(z)φ(w)=10時，結合情況2.4中情況的討論與φ(x)=6，可得此時方程(2)無解。

當φ(y)φ(z)φ(w)=12時，有φ(y)=φ(z)=1，φ(w)=12或φ(y)=φ(w)=1，φ(z)=12或φ(y)=12，φ(z)=φ(w)=1或φ(y)=1，φ(z)=2，φ(w)=6或φ(y)=1，φ(z)=6，φ(w)=2或φ(y)=2，φ(z)=1，φ(w)=6或φ(y)=2，φ(z)=6，φ(w)=1或φ(y)=6，φ(z)=1，φ(w)=2或φ(y)=6，φ(z)=2，φ(w)=1。由對稱性，不妨就φ(y)=φ(z)=1，φ(w)=12與φ(y)=1，φ(z)=2，φ(w)=6進行討論。

當φ(y)=φ(z)=1，φ(w)=12時，此時由方程(2)有Pφ(x)=4φ(x)+56，即有(P-4)φ(x)=56，而此時φ(x)=6，6?56，則此時方程(2)無解。

當φ(y)=1，φ(z)=2，φ(w)=6時，此時y=1,2，z=3,4,6，w=7,9,14,16，結合φ(x)=6可得，此時方程(2)無解。

當φ(y)φ(z)φ(w)=16時，有φ(y)=φ(z)=1，φ(w)=16或φ(y)=φ(w)=1，φ(z)=16或φ(y)=16，φ(z)=φ(w)=1或φ(y)=1，φ(z)=2，φ(w)=8或φ(y)=1，φ(z)=8，φ(w)=2或φ(y)=2，φ(z)=1，φ(w)=8或φ(y)=2，φ(z)=8，φ(w)=1或φ(y)=8，φ(z)=1，φ(w)=2或φ(y)=8，φ(z)=2，φ(w)=1或φ(y)=1，φ(z)=4，φ(w)=4或φ(y)=4，φ(z)=1，φ(w)=4或φ(y)=4，φ(z)=4，φ(w)=1。由于對稱性，不妨就φ(y)=φ(z)=1，φ(w)=16與φ(y)=1，φ(z)=2，φ(w)=8與φ(y)=1，φ(z)=4，φ(w)=4進行討論。

當φ(y)=φ(z)=1，φ(w)=16時，此時y=z=1,2，w=17,32,34,40,48,60，結合φ(x)=6，則可得此時方程(2)有滿足y≤z≤w的整數解(x,y,z,w)=(7,1,1,17)，(9,1,1,17)，(14,1,1,17)，(18,1,1,17)，(7,1,1,32)，(9,1,1,32)，(7,1,1,34)，(9,1,1,34)，(7,1,1,40)，(9,1,1,40)，(7,1,1,48)，(7,1,1,60)，(7,1,2,17)，(9,1,2,17)。

當φ(y)=1，φ(z)=2，φ(w)=8時，此時由方程(2)有Pφ(x)=4φ(x)+44，即有(P-4)φ(x)=44，而此時φ(x)=6，6?44，則此時方程(2)無解。

當φ(y)=1，φ(z)=4，φ(w)=4時，此時y=1,2，z=w=5,8,10,12，結合φ(x)=6，則可得此時方程(2)無解。

情況2.6當φ(x)=4

由于φ(y)φ(z)φ(w)≥6，則φ(y)，φ(z)，φ(w)三者中必有一數滿足φ(n)≥2，此處不妨令φ(w)≥2，則(φ(y)-1)(φ(z)-1)(φ(w)-2)≥0，因而

φ(y)φ(z)φ(w)≥2φ(y)φ(z)+φ(y)φ(w)+φ(z)φ(w)-2φ(y)-2φ(z)-φ(w)+2

因φ(y)φ(z)≥φ(y)+φ(z)-1，φ(y)φ(w)≥2φ(y)+φ(w)-2，φ(z)φ(w)≥2φ(z)+φ(w)-2，則有

φ(y)φ(z)φ(w)≥2φ(y)+2φ(z)-4

(8)

結合φ(x)=4，(4)與(8)有φ(y)φ(z)φ(w)≤φ(y)+φ(z)+φ(w)+6。因而，2φ(y)+2φ(z)-4≤φ(y)+φ(z)+φ(w)+6，則φ(y)+φ(z)≤10，因而φ(y)+φ(z)=2,3,4,5,6,7,8,9,10。

當φ(y)+φ(z)=2時，有φ(y)=φ(z)=1。此時y=z=1,2，結合φ(x)=4，則可得此時方程(2)有滿足y≤z≤w的整數解(x,y,z,w)=(5,1,1,35)，(5,1,1,45)，(5,1,1,70)，(5,1,1,90)，(5,1,2,14)，(5,1,2,18)，(5,1,2,35)，(5,1,2,45)，(5,1,2,10)，(5,2,2,7)，(5,2,2,9)，(5,2,2,6)，(5,2,2,4)，(5,2,2,5)，(8,1,1,6)，(8,1,1,4)，(8,1,2,7)，(8,1,2,9)，(8,1,2,6)，(8,1,2,4)，(8,2,2,3)，(10,1,1,14)，(10,1,1,18)，(10,1,1,35)，(10,1,1,45)，(10,1,1,10)，(10,1,2,7)，(10,1,2,9)，(10,1,2,6)，(10,1,2,4)，(10,1,2,5)，(10,2,2,3)，(12,1,1,14)，(12,1,1,21)，(12,1,2,7)，(12,1,2,4)。

當φ(y)+φ(z)=3時，有φ(y)=1，φ(z)=2或φ(y)=2，φ(z)=1.就φ(y)=1，φ(z)=2情況有y=1,2，z=3,4,6，結合φ(x)=4，則可得此時方程(2)有整數解(x,y,z,w)=(5,2,4,2)，(5,2,6,2)，(8,1,4,2)，(8,1,6,2)，(8,2,3,2)，(8,2,4,1)，(8,2,6,1)，(10,1,4,2)，(10,1,6,2)，(10,2,3,2)，(10,2,4,1)，(10,2,6,1)，(12,1,4,2)，(12,2,4,1)。

當φ(y)+φ(z)=4時，有φ(y)=2，φ(z)=2。此時y=z=3,4,6，結合φ(x)=4，可得此時方程(2)無解。

當φ(y)+φ(z)=5時，有φ(y)=1，φ(z)=4或φ(y)=4，φ(z)=1.就φ(y)=1，φ(z)=4情況有y=1,2，z=5,8,10,12，結合φ(x)=4，則可得此時方程(2)有整數解(x,y,z,w)= (5,1,10,2)，(5,2,5,2)，(5,2,10,1)，(10,1,5,2)，(10,1,10,1)，(10,2,5,1)。

當φ(y)+φ(z)=6時，有φ(y)=2，φ(z)=4或φ(y)=4，φ(z)=2。就φ(y)=2，φ(z)=4情況有y=3,4,6，z=5,8,10,12，結合φ(x)=4，可得此時方程(2)無解。

當φ(y)+φ(z)=7時，有φ(y)=1，φ(z)=6或φ(y)=6，φ(z)=1.就φ(y)=1，φ(z)=6情況有y=1,2，z=7,9,14,18，結合φ(x)=4，可得此時方程(2)有整數解(x,y,z,w)=(5,1,14,2)，(5,1,18,2)，(5,2,7,2)，(5,2,9,2)，(5,2,14,1)，(5,2,18,1)，(8,1,7,2)，(8,1,9,2)，(8,1,14,1)，(8,1,18,1)，(8,2,7,1)，(8,2,9,1)，(10,1,7,2)，(10,1,9,2)，(10,1,14,1)，(10,1,18,1)，(10,2,7,1)，(10,2,9,1)，(12,1,7,2)，(12,1,14,1)，(12,2,7,1)。

當φ(y)+φ(z)=8時，有φ(y)=2，φ(z)=6或φ(y)=6，φ(z)=2或φ(y)=4，φ(z)=4。

當φ(y)=2，φ(z)=6時，有y=3,4,6，z=7,9,14,18，結合φ(x)=4，可得此時方程(2)無解。

當φ(y)=4，φ(z)=4時，有y=z=5,8,10,12，結合φ(x)=4，可得此時方程(2)無解。

當φ(y)+φ(z)=9時，有φ(y)=1，φ(z)=8或φ(y)=8，φ(z)=1。當φ(y)=1，φ(z)=8，此時有y=1,2，z=15,16,20,24,30，結合φ(x)=4，可得此時方程(2)無解。

當φ(y)+φ(z)=10時，有φ(y)=2，φ(z)=8或φ(y)=8，φ(z)=2或φ(y)=4，φ(z)=6或φ(y)=6，φ(z)=4。

當φ(y)=2，φ(z)=8時，有y=3,4,6，z=15,16,20,24,30，結合φ(x)=4，可得此時方程(2)無解。

當φ(y)=4，φ(z)=6時，有y=5,8,10,12，z=7,9,14,18，結合φ(x)=4，可得此時方程(2)無解。

情況2.7φ(x)=2

情況2.7.1當φ(y)、φ(z)、φ(w)中僅有一數滿足φ(n)=1時，不妨令φ(y)=1，則y=1,2。

情況2.7.1.1當φ(z)、φ(w)中僅有一數滿足φ(n)=2時，不妨令φ(z)=2，且φ(w)≠1，此時x=z=3,4,6，則可得此時方程(2)有整數解(x,y,z,w)=(3,1,3,11)，(3,1,3,22)，(3,2,6,2)，(6,1,6,2)，(6,2,3,2)，(6,2,6,1)。

情況2.7.1.2當φ(z)、φ(w)都滿足φ(n)=2時，此時z=w=3,4,6，結合φ(x)=2，可得此時方程(2)無解。

情況2.7.1.3當φ(z)、φ(w)都滿足φ(n)>2時，則有(φ(z)-4)(φ(w)-4)≥0，即有

φ(z)φ(w)≥4(φ(z)+φ(w))-16

(9)

由于φ(xyzw)=4(φ(x)+φ(y)+φ(z)+φ(w))=4(3+φ(z)+φ(w))≥φ(x)φ(y)φ(z)φ(w)，結合式(9)有4(3+φ(z)+φ(w))≥2φ(z)φ(w)≥8(φ(z)+φ(w))-32，則有φ(z)+φ(w))≤11，因而φ(z)+φ(w))=8或φ(z)+φ(w))=10。

當φ(z)+φ(w))=8時，有φ(z)=φ(w)=4，則z=w=5,8,10,12，結合φ(x)=2，可得此時方程(2)無解。

當φ(z)+φ(w))=10時，有φ(z)=4，φ(w)=6或φ(z)=6，φ(w)=4。由于對稱性，現只對φ(z)=4，φ(w)=6的情況討論。此時z=5,8,10,12，w=7,9,14,18，結合φ(x)=2，可得此時方程(2)無解。

情況2.7.2當φ(y)、φ(z)、φ(w)中有兩數滿足φ(n)=1時，不妨令φ(y)=1，φ(z)=1，且φ(w)≠1.此時y=z=1,2，結合φ(x)=2，可得此時方程(2)有整數解(x,y,z,w)=(3,1,2,24)，(3,1,2,30)，(3,2,1,24)，(3,2,1,30)，(3,2,2,10)，(3,2,2,15)，(3,2,2,8)，(3,2,2,6)，(4,1,2,10)，(4,1,2,12)，(4,1,2,8)，(4,2,1,10)，(4,2,1,12)，(4,2,1,8)，(4,2,2,5)，(6,1,1,24)，(6,1,1,30)，(6,1,2,10)，(6,1,2,15)，(6,1,2,8)，(6,1,2,6)，(6,2,1,10)，(6,2,1,15)，(6,2,1,8)，(6,2,1,6)，(6,2,2,5)，(6,2,2,3)。

情況2.7.3當φ(y)、φ(z)、φ(w)都滿足φ(n)=1時，此時y=z=w=1,2，結合φ(x)=2，可得此時方程(2)無解。

情況2.7.4當φ(y)、φ(z)、φ(w)都滿足φ(n)≥2時，則有(φ(y)-2)(φ(z)-2)(φ(w)-2)≥0，則

φ(y)φ(z)φ(w)≥2φ(y)φ(z)+2φ(y)φ(w)+2φ(z)φ(w)-4(φ(y)+φ(z)+φ(w))+8

(10)

而φ(y)φ(z)≥2(φ(y)+φ(z))-4，φ(y)φ(w)≥2(φ(y)+φ(w))-4，φ(z)φ(w)≥2(φ(z)+φ(w))-4，則由(10)有φ(y)φ(z)φ(w)≥4(φ(y)+φ(z)+φ(w))-16。而由式(4)有4(2+φ(y)+φ(z)+φ(w))≥2φ(y)φ(z)φ(w)≥8(φ(y)+φ(z)+φ(w))-32，則有φ(y)+φ(z)+φ(w)≤10.從而有φ(y)+φ(z)+φ(w)=6,8,10。

情況2.7.4.1當φ(y)+φ(z)+φ(w))=6時，有φ(y)=φ(z)=φ(w)=2，此時y=z=w=3,4,6，結合φ(x)=2，可得此時方程(2)無解。

情況2.7.4.2當φ(y)+φ(z)+φ(w))=8時，有φ(y)=2，φ(z)=2，φ(w)=4或者φ(y)=2，φ(z)=4，φ(w)=2或者φ(y)=4，φ(z)=2，φ(w)=2.現不妨就φ(y)=2，φ(z)=2，φ(w)=4情況討論。此時y=z=3,4,6，w=5,8,10,12，結合φ(x)=2，可得此時方程(2)無解。

情況2.7.4.3當φ(y)+φ(z)+φ(w))=10時，有φ(y)=2，φ(z)=2，φ(w)=6或者φ(y)=2，φ(z)=6，φ(w)=2或者φ(y)=6，φ(z)=2，φ(w)=2或者φ(y)=2，φ(z)=4，φ(w)=4或者φ(y)=4，φ(z)=4，φ(w)=2或者φ(y)=4，φ(z)=2，φ(w)=4。

當φ(y)=2，φ(z)=2，φ(w)=6時，此時y=z=3,4,6，w=7,9,14,18，結合φ(x)=2，可得此時方程(2)無解。

當φ(y)=2，φ(z)=4，φ(w)=4時，此時y=3,4,6，z=w=5,8,10,12，結合φ(x)=2，可得此時方程(2)無解。

情況2.8φ(x)=1

情況2.8.1當φ(y)、φ(z)、φ(w)中僅有一數滿足φ(n)=1時，不妨令φ(y)=1。

情況2.8.1.1當φ(z)、φ(w)中僅有一數滿足φ(n)=2時，不妨令φ(z)=2，且φ(w)≠1，此時x=y=1,2，z=3,4,6，則可得此時方程(2)有整數解(x,y,z,w)=(1,1,6,24)，(1,1,6,30)，(1,2,3,24)，(1,2,3,30)，(1,2,4,10)，(1,2,4,12)，(1,2,4,8)，(1,2,6,10)，(1,2,6,15)，(1,2,6,8)，(1,2,6,6)，(2,2,3,10)，(2,2,3,15)，(2,2,3,8)，(2,2,3,6)，(2,2,4,5)，(2,2,6,5)，(2,2,6,3)。

情況2.8.1.2當φ(z)、φ(w)都滿足φ(n)=2時，此時x=y=1,2，z=w=3,4,6，則可得方程(2)有整數解(x,y,z,w)=(2,1,6,6)，(2,2,3,6)，(2,2,6,3)，(1,2,6,6)。

情況2.8.1.3當φ(z)、φ(w)都滿足φ(n)>2時，則有(φ(z)-4)(φ(w)-4)≥0，即有

φ(z)φ(w)≥4(φ(z)+φ(w))-16

(11)

由于φ(xyzw)=4(φ(x)+φ(y)+φ(z)+φ(w))=4(2+φ(z)+φ(w))≥φ(x)φ(y)φ(z)φ(w)，結合(11)有4(2+φ(z)+φ(w))≥2φ(z)φ(w)≥8(φ(z)+φ(w))-32，則有φ(z)+φ(w))≤10，因而φ(z)+φ(w))=8或φ(z)+φ(w))=10。

當φ(z)+φ(w))=8時，有φ(z)=φ(w))=4，此時z=w=5,8,10,12，結合φ(y)=1，可得此時方程(2)有整數解(x,y,z,w)=(2,1,5,10)，(2,1,10,5)，(1,1,10,10)，(2,2,5,5)，(1,2,5,10)，(1,2,10,5)。

當φ(z)+φ(w))=10時，有φ(z)=4，φ(w)=6或φ(z)=6，φ(w)=4。由于對稱性，現只對φ(z)=4，φ(w)=6的情況討論。此時z=5,8,10,12，w=7,9,14,18，結合φ(y)=1，可得此時方程(2)有整數解(x,y,z,w)=(2,1,5,14)，(2,1,5,18)，(2,1,8,7)，(2,1,8,9)，(1,1,8,14)，(1,1,8,18)，(2,1,10,7)，(2,1,10,9)，(1,1,10,14)，(1,1,10,18)，(2,1,12,7)，(1,1,12,14)，(2,2,5,7)，(2,2,5,9)，(1,2,5,14)，(1,2,5,18)，(1,2,8,7)，(1,2,8,9)，(1,2,10,7)，(1,2,10,9)，(1,2,12,7)。

情況2.8.2當φ(y)、φ(z)、φ(w)中有兩數滿足φ(n)=1時，不妨令φ(y)=1，φ(z)=1，且φ(w)≠1。結合φ(x)=1，可得此時，方程(2)無整數解。

情況2.8.3當φ(y)、φ(z)、φ(w)都滿足φ(n)=1時，結合φ(x)=1，可得此時方程(2)無整數解。

情況2.8.4當φ(y)、φ(z)、φ(w)都滿足φ(n)≥2時，則有(φ(y)-2)(φ(z)-2)(φ(w)-2)≥0，則

φ(y)φ(z)φ(w)≥2φ(y)φ(z)+2φ(y)φ(w)+2φ(z)φ(w)-4(φ(y)+φ(z)+φ(w))+8

(12)

而φ(y)φ(z)≥2(φ(y)+φ(z))-4，φ(y)φ(w)≥2(φ(y)+φ(w))-4，φ(z)φ(w)≥2(φ(z)+φ(w))-4，則由(12)有φ(y)φ(z)φ(w)≥4(φ(y)+φ(z)+φ(w))-16。而由式(4)有4(1+φ(y)+φ(z)+φ(w))≥2φ(y)φ(z)φ(w)≥8(φ(y)+φ(z)+φ(w))-32，則有φ(y)+φ(z)+φ(w)≤9，從而有φ(y)+φ(z)+φ(w)=6,8。

情況2.8.4.1當φ(y)+φ(z)+φ(w))=6時，有φ(y)=φ(z)=φ(w)=2。此時方程(2)無整數解。

情況2.8.4.2當φ(y)+φ(z)+φ(w))=8時，有φ(y)=2，φ(z)=2，φ(w)=4或者φ(y)=2，φ(z)=4，φ(w)=2或者φ(y)=4，φ(z)=2，φ(w)=2。此時，方程(2)有滿足x≤y≤z≤w的整數解(x,y,z,w)=(1,3,3,12)。

綜上所有情況的討論，可得結論。

2 結束語

由定理1可知：在方程(2)滿足x≤y≤z≤w的整數解中，x,y,z,w互不相同的解有22組，由對稱性每組可確定24組解，此時可確定528組解；x,y,z,w有2個數相同的解有45組，由對稱性每組可確定12組解，此時可確定540組解；x,y,z,w有兩對數相同的解有2組，由對稱性每組可確定6組解，此時可確定12組解，因而方程(2)共有1 080組整數解。