基于VPSO-SVM的磷酸鐵鋰電池壽命預測

王 寧，劉憶恩，江柯成，陳澤華

(1.太原理工大學 電氣與動力工程學院， 太原 030024；2.山西沃特海默新材料科技股份有限公司， 太原 030024；3.東莞塔菲爾新能源科技有限公司， 太原 030024；4.太原理工大學 大數據學院， 太原 030024)

鋰離子電池憑借其獨特優勢，在民用、軍用甚至航天領域得到了廣泛使用，如儲能系統中河北張北風光儲輸項目、美國西弗吉尼亞32 MW勞雷爾山儲能電站等均采用鋰離子電池。同時，在航空航天等領域，其取代了以往的氫鎳、鎳鎘蓄電池，目前成為了第三代衛星儲能電源，如SMART-1月球探測器、STRV-1d航天器以及中國新一代北斗導航衛星雙星系統等都采用其作為儲能電源。但在使用過程中，電池本身材料的損耗、環境的動態變化以及不同的使用方式等因素都會影響電池的充放電能力，使其健康狀況產生不同程度的衰退[1-3]，最終導致電池的壽命終了。作為系統供能的一部分，電池的損壞會導致整個系統發生故障，從而導致財產損失甚至造成人員傷亡。因此，準確預測電池的SOH可以在很大程度上確保其安全可靠的運行[4]。目前，國內外所采用的壽命預測方法可分為兩種：一種是基于經驗的方法，另一種是基于性能的方法[5]。用于優化的智能算法主要有遺傳算法(genetic algorithm，GA)[6-7]、粒子群優化算法(particle swarm optimization，PSO)[8-9]、人工魚群算法[10]等。文獻[11]針對相關向量機的核函數進行了組合改進，提高了其性能及預測精度。文獻[12]采用了人工蜂群算法來對電池模型的參數進行辨識，提高了解的優化精度。文獻[13]中所提出的改進算法對于多峰似然函數下粒子的覆蓋效率無法保證，因此降低了其適用性。文獻[6]利用GA算法優化參數時，雖然在一定程度上避免了局部最小的問題，但是并沒有從根本上解決。文獻[9]采用了PSO-SVM模型，雖然提高了預測精度，但其對于參數的優化依然存在不足。

本文采用磷酸鐵鋰電池在循環使用過程中所產生的數據，數據來自東莞某科技有限公司。本實驗對于電池的影響因素進行了充分考慮，以循環次數、內阻以及溫度作為輸入。針對SVM模型參數難以尋優的問題，利用VPSO可以避免局部最小以及早熟等優點來提高SVM的性能。實驗證明：所提出的方法可以有效提升模型的精確性。

1 PSO算法介紹

粒子群優化算法(particle swarm optimization，PSO)是一種群優化算法，其算法受到了鳥群尋找食物的啟發，搜尋食物的過程，即粒子尋找最優解的過程。假設粒子群的規模為n，搜索的空間為D維，粒子i(i∈1,2,…,n)的位置為xi=(xi1,xi2,…,xiD)，其速度為vi=(vi1,vi2,…,viD)，粒子i的最優位置為pi=(pi1,pi2,…,piD)，粒子群最佳的位置為pg=(pg1,pg2,…,pgD)，在k+1次的迭代中，其位置更新為：

(1)

2 VPSO算法介紹

PSO算法是根據個體粒子以及群體的記錄，通過相互合作的方式向著最優解的方向進行搜尋。但在PSO搜索后期，存在局部最優問題以及過早收斂等問題，而且對于初始參數的依賴度過高。因此，針對上述問題，提出改進算法[14]，即基于“粒子速度臨界閾值變異”的算法。

其變異思路如下：

設定一個速度閾值，當個體粒子的速度vid沒有達到這個閾值時，給粒子一個加速沖量，使得其初始化，其速度在區間[-vmax,vmax]上，從而加大了粒子的搜索空間，實現了變異，防止局部最小問題的發生，最終得到全局最佳解。閾值T取T→0，其變異過程可用式(2)表示：

(2)

變異強度控制：

在VPSO中，變異系數起著很大的作用，如果λ值過小，則難以達到預期目標；如果λ值過大，則會導致較大的初始化速度，影響粒子群的收斂性，還可能導致其不斷變異，錯過全局的最佳解。因此，λ值的大小可根據粒子速度變化和空間范圍確定：

(3)

粒子經過變異后，會使其失去記錄的最優位置，只能保留全體的最優位置，此時，個體的最優位置為：

(4)

PSO算法存在局部最優以及早熟收斂等缺陷，為了應對上述不足，VPSO算法提出當粒子在空間中的搜索速度小于所設定的閾值時，可以給其一個加速沖量，使其在空間中的位置重新隨機定位，因此擴展了粒子的搜索空間，實現了變異以達到全局最優目標，可以有效避免陷入局部最優，也可以防止搜索后期早熟現象的發生。

VPSO算法的步驟可用圖1表示。

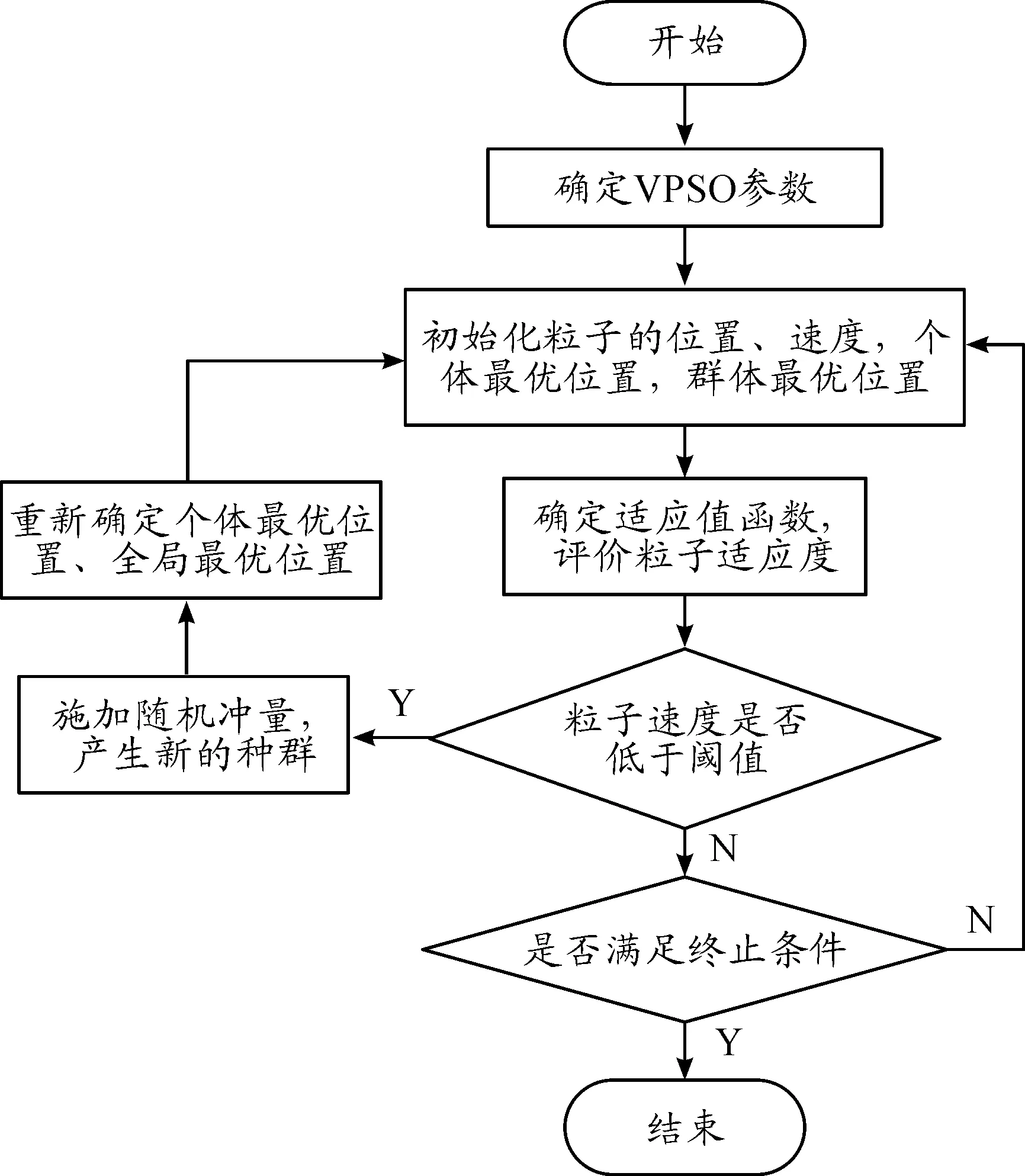
圖1 VPSO算法流程

3 VPSO-SVM模型

在SVM中，其參數c和g對預測結果的準確性有較大的影響。因此，將SVM的2個參數作為VPSO的優化變量，提出VPSO-SVM算法，具體步驟如下：

2) 對VPSO的各種參數進行初始化操作，其中包括慣性因子ω，加速常數c1和c2，群體的規模，迭代次數tmax，粒子最佳位置pbest以及全局最佳位置gbest；

3) 評估粒子函數的適應性，并將粒子的每個位置與其記錄的最佳位置進行對比，若不及所記錄的最好位置，則當前位置用pbest代替；將當前適應度與群體紀錄的最好位置進行對比，若不及所記錄的最好位置，則當前位置用所記錄的最好位置代替；

4) 當粒子的速度低于所設定的閾值時，則給予粒子一個加速度，從而調整SVM的參數，并返回2)；

5) 判斷當前能否滿足停止條件，即達到了誤差和最大迭代次數的要求，若符合，則將全局最優粒子映射為SVM的參數；若不符合，則返回2)；

6) 將局部優化完成后的參數進行編碼，若符合停止的條件，則輸出結果；若不符合，則返回2)，最終達到最優結果。

上述步驟可用圖2表示。

圖2 VPSO-SVM算法流程

4 實驗

4.1 數據獲取

本實驗所使用的數據來自東莞某科技有限公司。單體電池的額定電池容量為120 Ah，充電截止電壓為3.65 V，放電截止電壓為2.5 V，串聯形成電池組。輸入變量為循環次數、內阻以及溫度，輸出變量為電池組的可用容量。

數據獲取采用如下實驗方法：恒定室溫下使用電池測試設備對電池組進行2 000次的循環壽命測試。首先，開始充電操作，電流大小為0.5 C，當達到總充電截止電壓時，開始恒壓充電，停止充電直到其電流小于0.05 C。此時，電池需要放置30 min，然后對其恒流放電，電流大小為1 C，直到達到總放電截止電壓時停止，再次將電池放置30 min，此時完成了一個測試周期，然后再次進行實驗。在實驗過程中，記錄電池的放電容量、循環次數、內阻以及溫度。隨機從數據中選取30%的數據作為測試集，其余作為訓練集。表1為部分輸入數據。

表1 輸入數據(部分)

4.2 實驗結果與分析

獲取實驗數據后，分別用SVM、GA-SVM[7]、PSO-SVM[8]以及VPSO-SVM算法進行實驗對比，圖3～6分別為上述模型的預測對比圖，圖7為GA、PSO以及VPSO算法的尋優曲線圖，表2為各模型的預測結果比較。

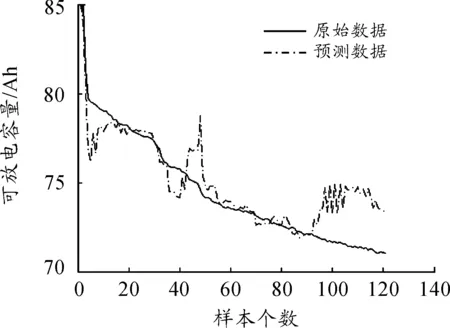
圖3 SVM預測對比

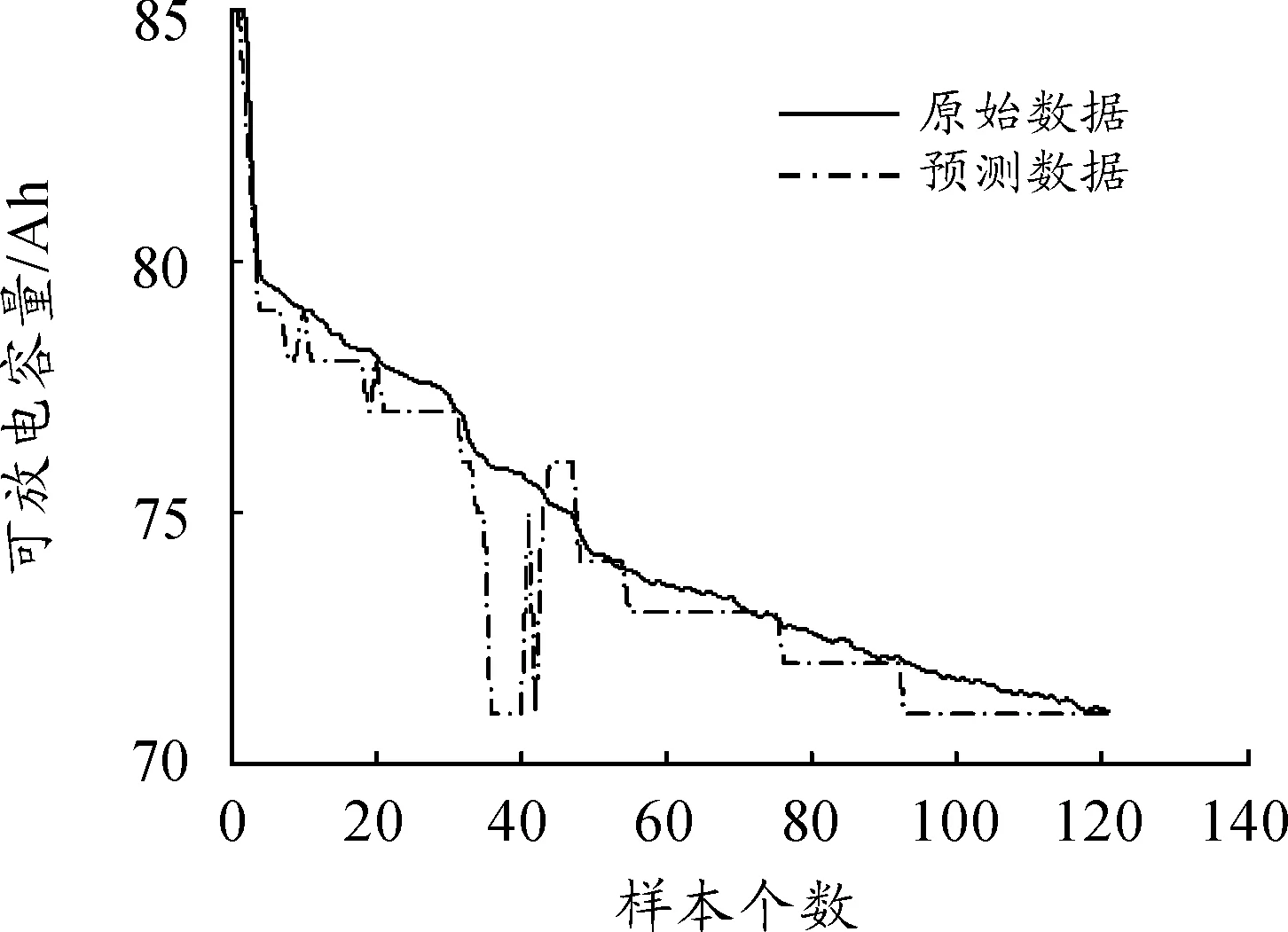
圖4 GA-SVM預測對比

圖5 PSO-SVM預測對比

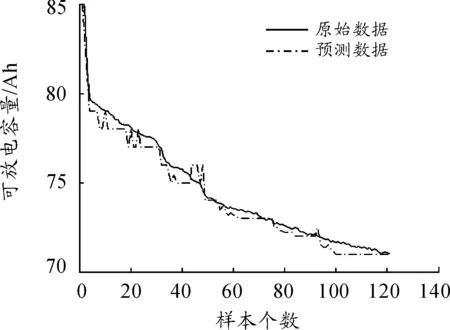
圖6 VPSO-SVM預測對比

圖7 尋優曲線

模型平方相關系數/%均方誤差/%SVM77.062.44GA-SVM88.521.47PSO-SVM89.201.06VPSO-SVM95.020.53

從圖3～6和表2中可以看出：VPSO-SVM算法誤差和平方相關系數都比其他3種模型優秀，并且VPSO-SVM算法的預測值與真實值的擬合程度較高，預測結果較好，說明VPSO算法對于優化SVM參數具有較好的效果，從而驗證了VPSO算法的有效性。從圖7可以看出：GA和PSO算法經常陷入局部最優，而VPSO算法具有較快的全局收斂速度和強大的全局搜索能力，可以有效避免早熟收斂問題。

5 結束語

采用常規方法對SVM參數進行尋優時，會出現局部最小等問題，因此本文利用VPSO來優化SVM的參數。通過對基于數據集的Matlab對比試驗分析證明：VPSO-SVM模型具有較好的學習能力和泛化能力，并且其精確性較高，是一種有效的SVM參數尋優算法；VPSO作為PSO目前的新晉改進算法，在參數尋優方面的發展才剛剛開始，接下來的工作除了優化提高精確性外，還可以在減少尋優時間上有所發展。