基于自適應控制的非線性多智能體系統(tǒng)一致性

唐朝君

(重慶理工大學 理學院， 重慶 400054)

由于當前多智能體系統(tǒng)在分布式傳感器網(wǎng)絡、編隊控制、信息融合和蜂擁等問題中的廣泛應用,對多智能體系統(tǒng)的研究吸引了不同領域研究學者的廣泛關注。一致性是多智能體系統(tǒng)協(xié)調(diào)控制研究的基礎,也是多智能體系統(tǒng)研究中最重要和最基本的一個問題。一致性是指通過設計恰當?shù)姆植际娇刂茀f(xié)議,使系統(tǒng)中的智能體就某些關鍵的量趨于一致。根據(jù)系統(tǒng)中是否有領導智能體,可以將一致性分為兩類,即無領導的一致性和領導跟隨一致性。

1995年，Vicsek等[1]提出了一個簡單卻十分有趣的離散時間多智能體系統(tǒng)模型,通過仿真演示了系統(tǒng)中所有的智能體最終以共同的方向前進。2003年，Jadbabaie等[2]利用矩陣理論和代數(shù)圖論的方法首次給出了Vicsek模型的理論解釋。Olfati-Saber和Murray[3]對連續(xù)時間多智能體系統(tǒng)的一致性研究做了開創(chuàng)性的工作，分別研究了固定和切換網(wǎng)絡拓撲下的一致性問題，以及帶有單一時滯的一致性問題。隨后,Ren等[4]研究了更為一般的網(wǎng)絡拓撲，給出了系統(tǒng)解決一致性所需的最弱的拓撲條件。隨著一致性問題研究的不斷深入,發(fā)展了一系列的重要的子課題，主要包括具有通信時滯的一致性、帶有測量噪聲的一致性、有限時間一致性、基于時間觸發(fā)機制的一致性和隨機網(wǎng)絡拓撲下的一致性問題等，具體參見文獻[5]。

在實際應用中，絕大多數(shù)的物理系統(tǒng)本質(zhì)上都是非線性系統(tǒng)。因此，對非線性多智能體系統(tǒng)一致性的研究具有重要意義。近年來，對非線性多智能體系統(tǒng)一致性的研究得到了一些有趣的結(jié)果。受同步理論的啟發(fā)，文獻[6-7]在一致性協(xié)議中引入了非線性函數(shù)來描述智能體內(nèi)在的非線性動態(tài)。針對有向網(wǎng)絡拓撲，提出了廣義代數(shù)連通度的概念,并用其得到了一致性的充分條件。文獻[8-9]利用牽制控制(pinning control)研究了二階非線性多智能體系統(tǒng)的領導-跟隨一致性問題。文獻[10]研究了非線性多智能體系統(tǒng)的有限時間一致性問題。文獻[11]研究了非線性多智能體系統(tǒng)的包含控制問題。

在現(xiàn)有大多數(shù)對一致性問題研究的文獻中， 所給出的一致性協(xié)議中都需要用到網(wǎng)絡拓撲所對應的Laplacian 矩陣特征值的信息， 這是一個全局的信息，因此這些控制協(xié)議并非嚴格意義的分布式控制協(xié)議。為了解決這個問題，一些研究學者提出了基于自適應的控制協(xié)議。目前，對基于自適應控制協(xié)議的一致性的研究已經(jīng)得到了一些有趣結(jié)果[12-15]。另外，文獻[6-11]中都是假設系統(tǒng)中的智能體具有相同的非線性動態(tài)，而對具有不同本質(zhì)非線性動態(tài)多智能體系統(tǒng)一致性的研究還鮮有報道。基于非線性動態(tài)的參數(shù)化分解，Yu等[16]對具有不同本質(zhì)非線性動態(tài)多智能體系統(tǒng)提出了一種基于自適應的控制協(xié)議來追蹤同樣具有未知非線性動態(tài)的領導智能體。受文獻[16]的啟發(fā)，本文研究具有不同本質(zhì)非線性動態(tài)多智能體系統(tǒng)的一致性問題。與文獻[16]相比，本文的創(chuàng)新之處主要體現(xiàn)在兩個方面：① 本文研究的是無領導的一致性問題，適用于更為一般的多智能體系統(tǒng)；② 文獻[16]只研究了無向網(wǎng)絡拓撲，本文分別研究了無向和有向網(wǎng)絡拓撲。值得注意的是，有向網(wǎng)絡拓撲更加符合實際應用，而無向網(wǎng)絡拓撲可視為有向網(wǎng)絡拓撲的特例。

1 問題描述

考慮由n個智能體構成的多智能體系統(tǒng)。智能體i的動力學模型為

(1)

式中：xi∈R是智能體i的狀態(tài)；ui(t)∈R是智能體i的控制輸入；fi(xi,t)∈R是智能體i自身動力學的非線性函數(shù)。

假設非線性函數(shù)fi(xi,t)滿足如下Lipschitz條件:

|fi(xi,t)-fi(xj,t)|≤l|xi-xj|

(2)

式中：xi,xj∈R;l>0為正常數(shù)。上述條件用于保證系統(tǒng)(1)解的存在性和唯一性。本文研究具有不同非線性動態(tài)的多智能體系統(tǒng)一致性問題，即對每個智能體設計分布式的控制協(xié)議ui，使所有智能體的狀態(tài)趨于一致。具體問題由如下定義給出：

定義1若系統(tǒng)(1)的解在任意初始條件下滿足

則稱多智能體系統(tǒng)(1)解決一致性問題。

本文利用有向圖來描述系統(tǒng)中智能體之間的拓撲結(jié)構。有向圖G由一個頂點集V和邊集E組成，其中V={1,2,…,n}，頂點i表示智能體i，E={(i,j)|i,j∈V}。若智能體i能接收到智能體j的信息，則(j,i)∈E，否則(j,i)?E。若(j,i)∈E， 則稱頂點j是頂點i的鄰居或者智能體j是智能體i的鄰居。從vi1到vik的一條路徑是由一系列不同的頂點vi1,vi2,…,vik構成，并且這些頂點滿足(vij,vij+1)∈E,j=1,2,…,k-1。如果從G中任一頂點到另外一頂點都有路徑存在，則稱G是強連通的；如果G中至少有一個頂點到其他頂點都有路徑存在，則稱G包含生成樹。對于有向圖G，如果(i,j)∈E蘊含著(j,i)∈E，那么稱G是無向圖；若無向圖G包含生成樹，則稱G是連通的。

圖G的Laplacian矩陣L=[lij]∈Rn×n定義為

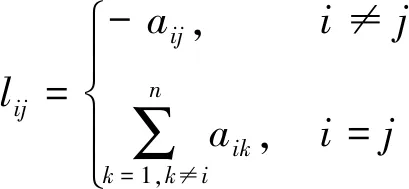
Laplacian矩陣在一致性問題的研究中具有非常重要的作用， 它具有下面的性質(zhì)[4]:

引理1 0是L的特征值， 1n=(1,1,…,1)T∈Rn是對應的特征向量，其他非零特征值的實部全部大于0；0是L代數(shù)簡單的特征值當且僅當圖G包含生成樹。

2 主要結(jié)果

本節(jié)給出分布式的控制協(xié)議，使系統(tǒng)(1)能解決一致性問題。假設非線性動態(tài)fi(xi,t)可進行線性參數(shù)化:

式中：φi(xi,t)∈Rm為已知的基函數(shù)向量，θi∈Rm為未知的常數(shù)參數(shù)向量。

注1本文假設智能體的非線性動態(tài)可以進行線性參數(shù)化。線性參數(shù)化的模型在經(jīng)典的自適應控制中已經(jīng)被廣泛研究[17-18]。文獻[16，19-21]對線性參數(shù)化的多智能體系統(tǒng)進行了研究。

使用如下的分布式控制協(xié)議：

(3)

首先研究固定拓撲的情形，此時系統(tǒng)的通信拓撲保持不變。利用協(xié)議(3)，系統(tǒng)(1)可以寫成下面的向量形式：

(4)

定理1假設系統(tǒng)的通信拓撲G連通。利用協(xié)議(3)， 系統(tǒng)(1)解決一致性問題。

則

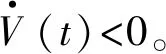
G是連通的無向圖，則L是對稱陣，而且存在正交陣U=(u1,u2,…,un)∈Rn×n，使得

UTLU=diag{λ1,λ2,…,λn}

eTLe=eTUdiag{λ1,λ2,…,λn}UTe=

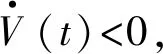
對于有向網(wǎng)絡拓撲， 容易得到下面的結(jié)論:

定理2假設系統(tǒng)的通信拓撲G是平衡圖且包含生成樹。利用協(xié)議(3)，系統(tǒng)(1)解決一致性問題。

證明使用定理1證明中的記號。注意到

由于G是平衡圖且包含生成樹， 由引理2可得

在實際應用中，由于障礙物的存在或者個體之間的相互影響，系統(tǒng)中的通信拓撲往往是時變的，因此研究時變拓撲下的一致性問題更具有實際意義。設P={G1,G2,…,Gs}為系統(tǒng)所有可能通信拓撲的集合， 其中m<+∞。為了描述時變拓撲， 定義分段定常切換信號:σ(t):[0,+∞)→J={1,2,…,s}。因此， 時刻t時系統(tǒng)的通信拓撲為Gσ(t)，簡記為Gσ。此時，系統(tǒng)(4)變?yōu)?/p>

(5)

定理3假設系統(tǒng)的通信拓撲Gi,?i∈J連通。利用協(xié)議(3)，系統(tǒng)(1)解決一致性問題。

與定理1的證明方法相同，可得

注意到Gσ為連通的無向圖，可得

eTLσe≥λ2(Lσ)eTe

3 數(shù)值模擬

本小節(jié)給出2個實例來驗證本文理論結(jié)果的正確性。考慮1個含有5個智能體的多智能體系統(tǒng)，智能體i的非線性動態(tài)可以參數(shù)化為

fi(xi,t)=[xisint,xicost]θi,i=1,2,…,5

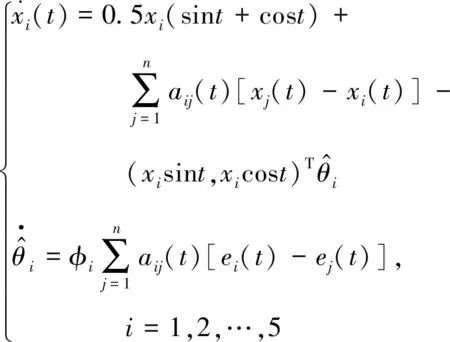
例1設系統(tǒng)的通信拓撲如圖1所示。為方便起見， 設圖中每條邊的權值均為1。智能體的初始位置隨機地選取為x(0)=(2,1,3,5,8)T和x(0)=(1,5,2,4,3)T，在協(xié)議(3)的作用下，智能體的狀態(tài)隨時間的變化曲線如圖2、3所示。顯然，智能體的狀態(tài)隨著時間的變化趨于一致，與定理1的結(jié)論相符。

圖1 系統(tǒng)的通信拓撲G1

圖2 智能體的狀態(tài)曲線1

圖3 智能體的狀態(tài)曲線2

例2設系統(tǒng)的通信拓撲如圖4所示。為方便起見， 設圖中每條邊的權值均為1。顯然G2是平衡圖且包含生成樹。智能體的初始位置隨機地選取為x(0)=(2,1,3,5,8)T和x(0)=(1,5,2,4,3)T。在協(xié)議(3)的作用下，智能體的狀態(tài)隨時間的變化曲線如圖5、6所示。顯然，智能體的狀態(tài)隨著時間的變化趨于一致，與定理2的結(jié)論相符。

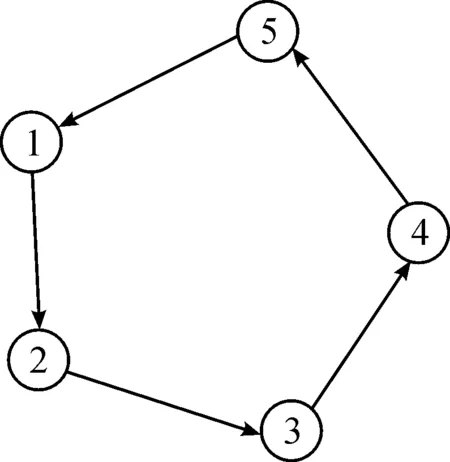
圖4 系統(tǒng)的通信拓撲G2

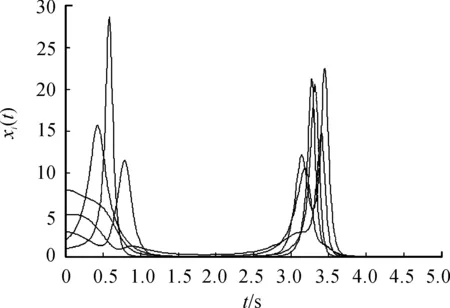
圖5 智能體的狀態(tài)曲線3

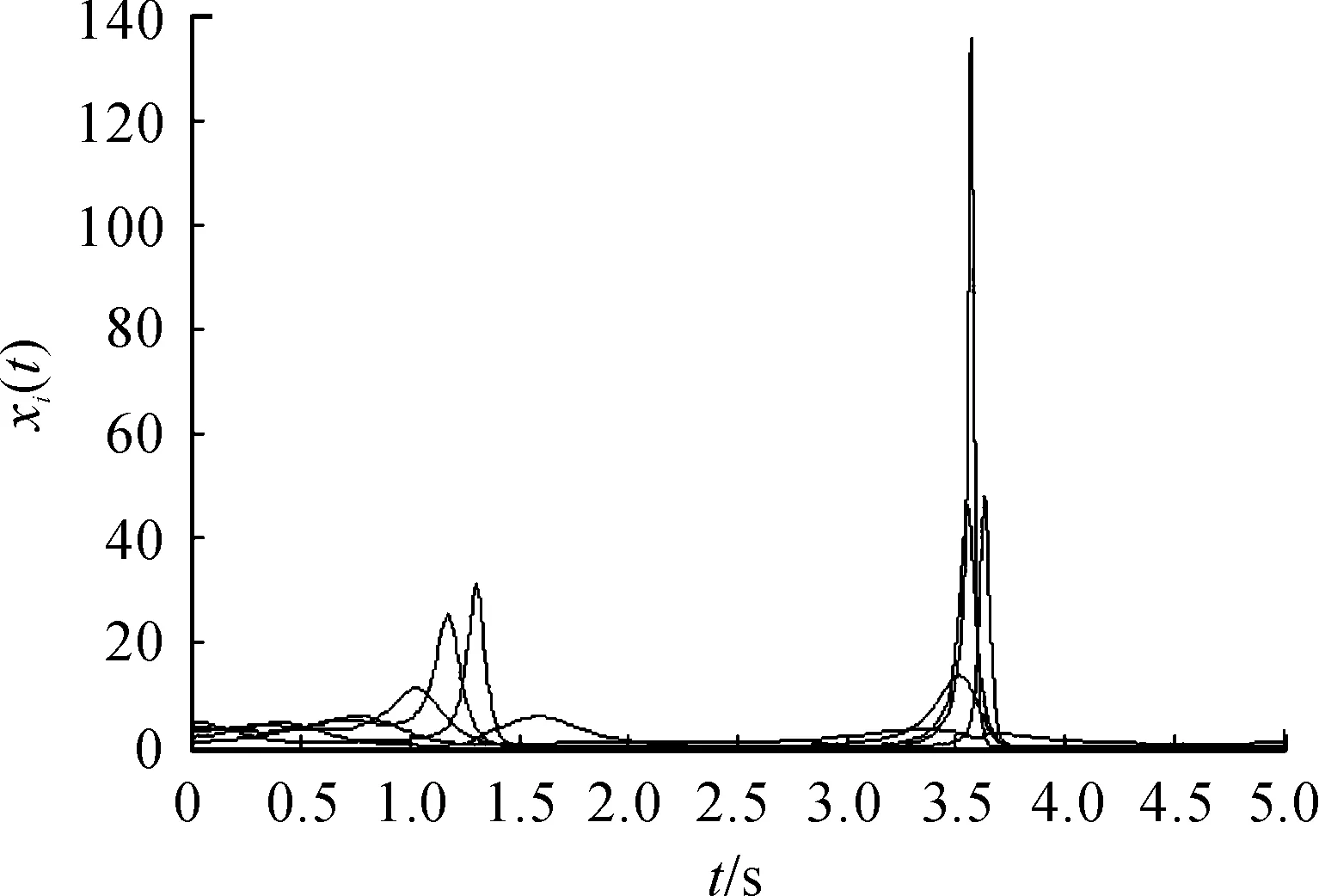
圖6 智能體的狀態(tài)曲線4

4 結(jié)束語

針對具有未知和不同非線性動態(tài)的多智能體系統(tǒng)，基于非線性動態(tài)的線性參數(shù)化分解的方法，給出了基于自適應的一致性控制協(xié)議。利用代數(shù)圖論、矩陣理論和Lyapunov的方法進行穩(wěn)定性分析。對于無向拓撲，當通信拓撲連通時，所給的協(xié)議解決一致性問題；對于有向拓撲，當系統(tǒng)的通信拓撲是平衡圖且包含生成樹時，所給的協(xié)議解決一致性問題；對于切換網(wǎng)絡拓撲，當系統(tǒng)所有可能的通信拓撲連通時，所給的協(xié)議解決一致性問題。最后通過仿真實例驗證了理論結(jié)果的正確性和有效性。