氣力推進艇螺旋槳靜態推力計算及檢測試驗

袁善坤，儲江偉，李洪亮，詹長書，張民安

(東北林業大學 交通學院， 哈爾濱 150040)

氣力推進艇是由發動機驅動后置螺旋槳旋轉產生向后的推力，使其依靠空氣動力在水中行駛[1]，主要應用于水面、雪地、冰面、沼澤等一般船舶無法行駛的特殊地段，供人們進行旅游觀光、生態勘察、救災救援以及運輸作業等[2-3]。國外對于氣力推進艇的研究開展較早，形成了較完整的理論設計、工業制造及實際應用體系。

氣力推進艇螺旋槳的靜態推力是在氣力推進艇不動的條件下，測試的螺旋槳產生的推力[3]。螺旋槳靜態推力是氣力推進艇動力系統匹配和螺旋槳應用選型的主要技術參數，對螺旋槳的實際應用具有指導意義。通過編程計算和試驗檢測氣力推進艇螺旋槳的靜態推力，可為進一步優化螺旋槳的翼型設計和提高使用性能提供參考[4]。

1 螺旋槳推力計算方法

1.1 基于葉元體理論的推力計算

將螺旋槳葉片沿徑向細分為多個離散的截面稱為葉元體，如圖1所示。對于每個葉元體只分析其軸向速度和角速度分量，忽略其他截面的誘導流，且對每部分進行獨立地分析，求出任意半徑r上的葉元體的作用力。

在圖1中的AA截面處，取dr段的葉元體進行分析。令幾何螺旋角為θ，攻角為αk。當流體以速度V1流向此葉元體時,流體軸向速度矢量V0和流體角速度矢量V2，并產生了升力L和阻力D，如圖2所示。圖2中，Q為驅動轉矩，T為推力[4]。

推力和升力方向之間的角度差定義為φ：

φ=θ-αk

(1)

將升力dL分解為沿螺旋槳軸向的分力dLα和旋轉方向的分力dLt,；將升力dD分解為沿螺旋槳軸向的分力dDα和旋轉方向的分力dDt。 葉元體的推力dT和轉矩dQ可以表達為[5]：

dT=dLa-dDa=dL·cosφ-dD·sinφ

(2)

(3)

葉元體產生力區域面積是c·dr，c為葉片弦長，則葉元體所受的升力與阻力表達式為[6]：

(4)

(5)

式中：CL為升力系數；CD為阻力系數；ρ為空氣密度，1.225 kg/m3。

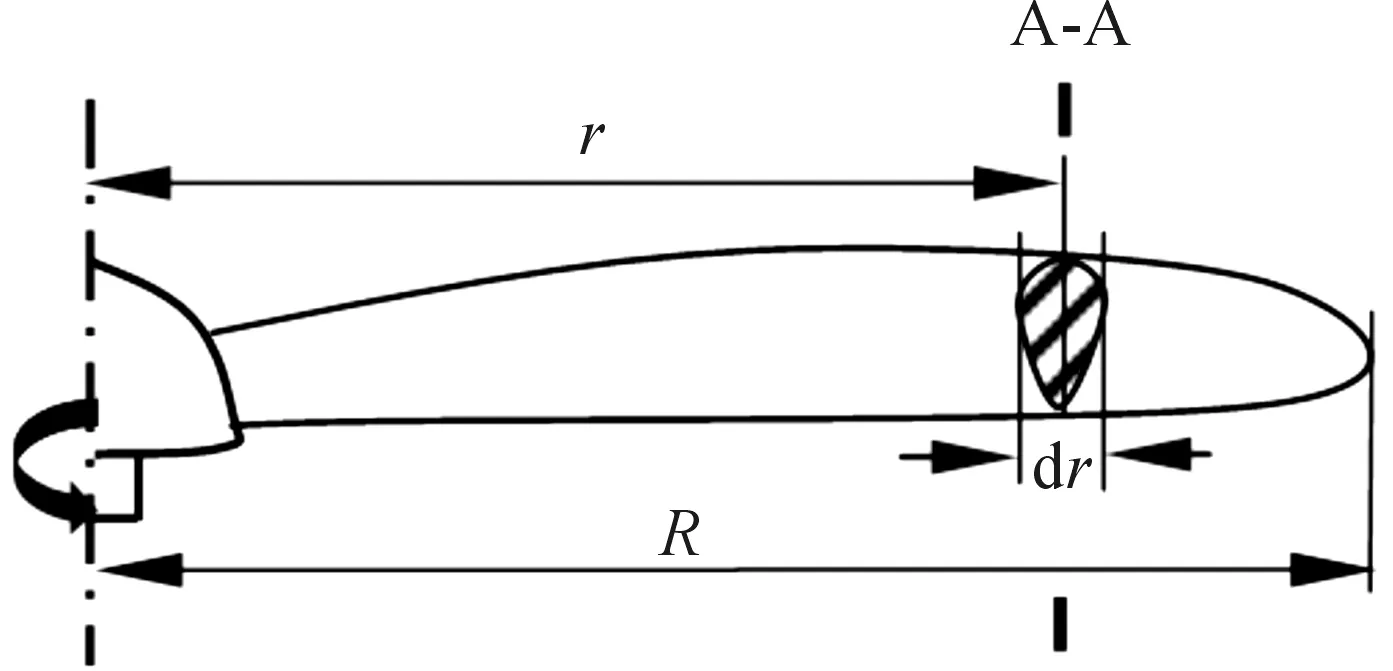
圖1 葉元體截取位置

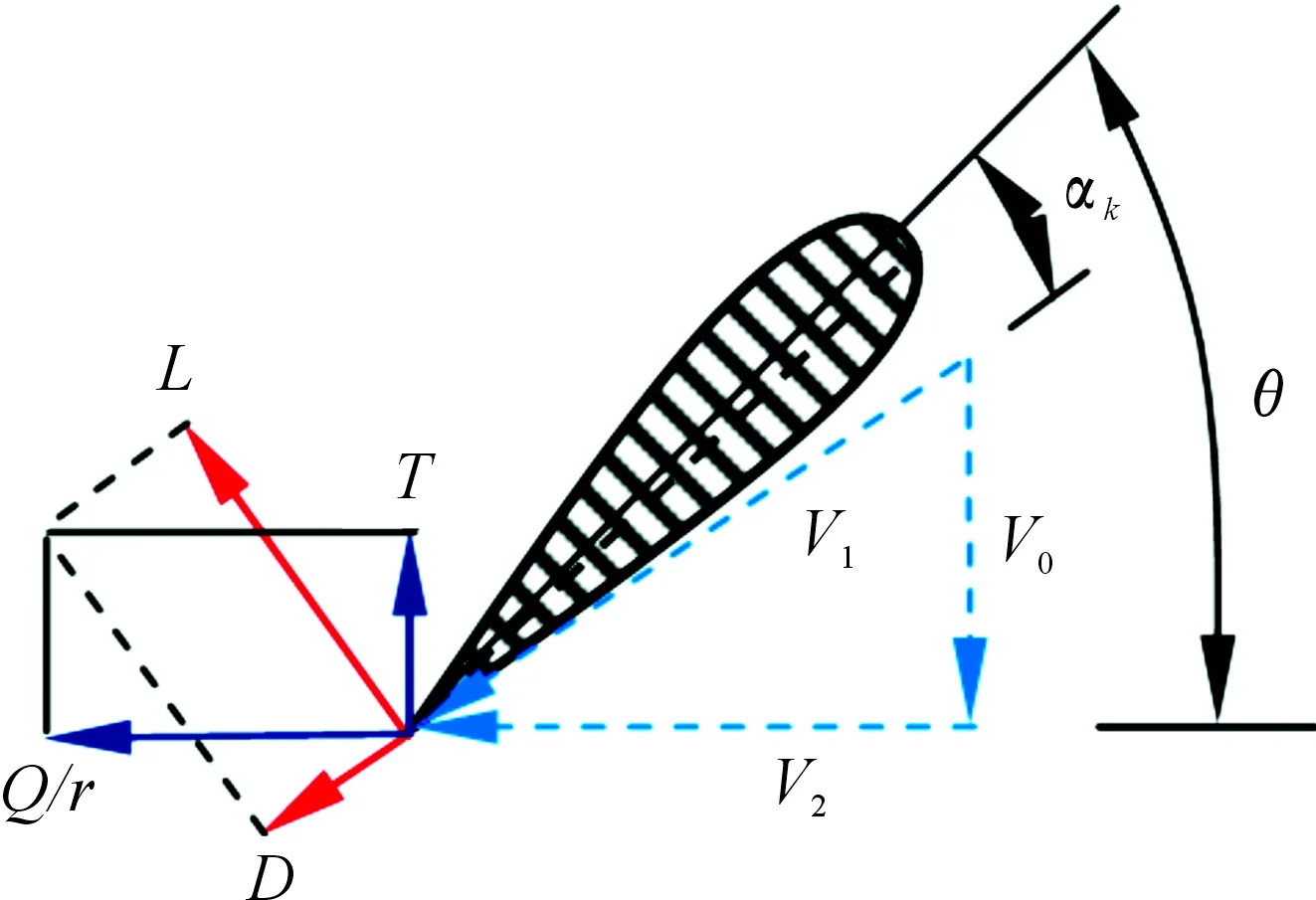
圖2 葉元體截面速度與作用力分析

當螺旋槳葉片的數量為B時，則

(6)

(7)

根據圖2所示，流體的合速度V1和攻角αk可以表達為：

(8)

αk=θ-tan-1(V0/V2)

(9)

式中：V0等于氣力推進艇的前進速度Vinf，V2等于葉元體旋轉的線速度ωr。

引入軸向誘導因子a和周向誘導因子b，則V0和V2可以表達為[7]

V0=Vinf+a·Vinf

(10)

V2=ωr-b·ωr

(11)

1.2 基于動量守恒理論的推力計算

假設螺旋槳在無限的靜止流體中以速度Vinf前進，應用運動轉換原理，即認為螺旋槳是固定的且被包在空氣流管里，空氣自無窮遠前方以速度Vinf流向螺旋槳。

根據動量守恒定理，作用在流體上的力等于單位時間內流體的動量的變化量[8-9]，則在葉元體上產生推力的表達式為：

dT=ΔP=dm·ΔV=ρ2πrdrV0(Vslip-Vinf)

(12)

式中： ΔP為動量的變化量；dm為葉元體質量；ΔV為速度的變化量；Vslip為滑流速度(m/s)。

由伯努利方程和動量守恒，可知螺旋槳盤面的軸向速度V0是空氣自由流速Vinf和氣流速度的平均值Vslip[10]：

V0=(Vinf+Vslip)/2

(13)

則

Vslip=Vinf(1+2a)

(14)

因此，由動量守恒理論得到的螺旋槳推力為：

(15)

根據角動量守恒，考慮其與軸向速度的變化相結合可以證明滑流角速度是螺旋槳盤r處值的2倍，即

Vθ=2bωr

(16)

即

(17)

螺旋槳總體推力T及所需的驅動轉矩Q等于其徑向葉元體推力dT和轉矩dQ的總和，即

T=∑dT

(18)

Q=∑dQ

(19)

2 螺旋槳推力及推力系數計算

2.1 迭代計算法及編程

上述式(6)～(9)(15)和(17)中是含有4個未知變量的dT、 dQ、a和b的方程，可以利用迭代的方法求出未知數。采用Matlab編寫計算程序的流程，如圖3所示。計算過程如下：

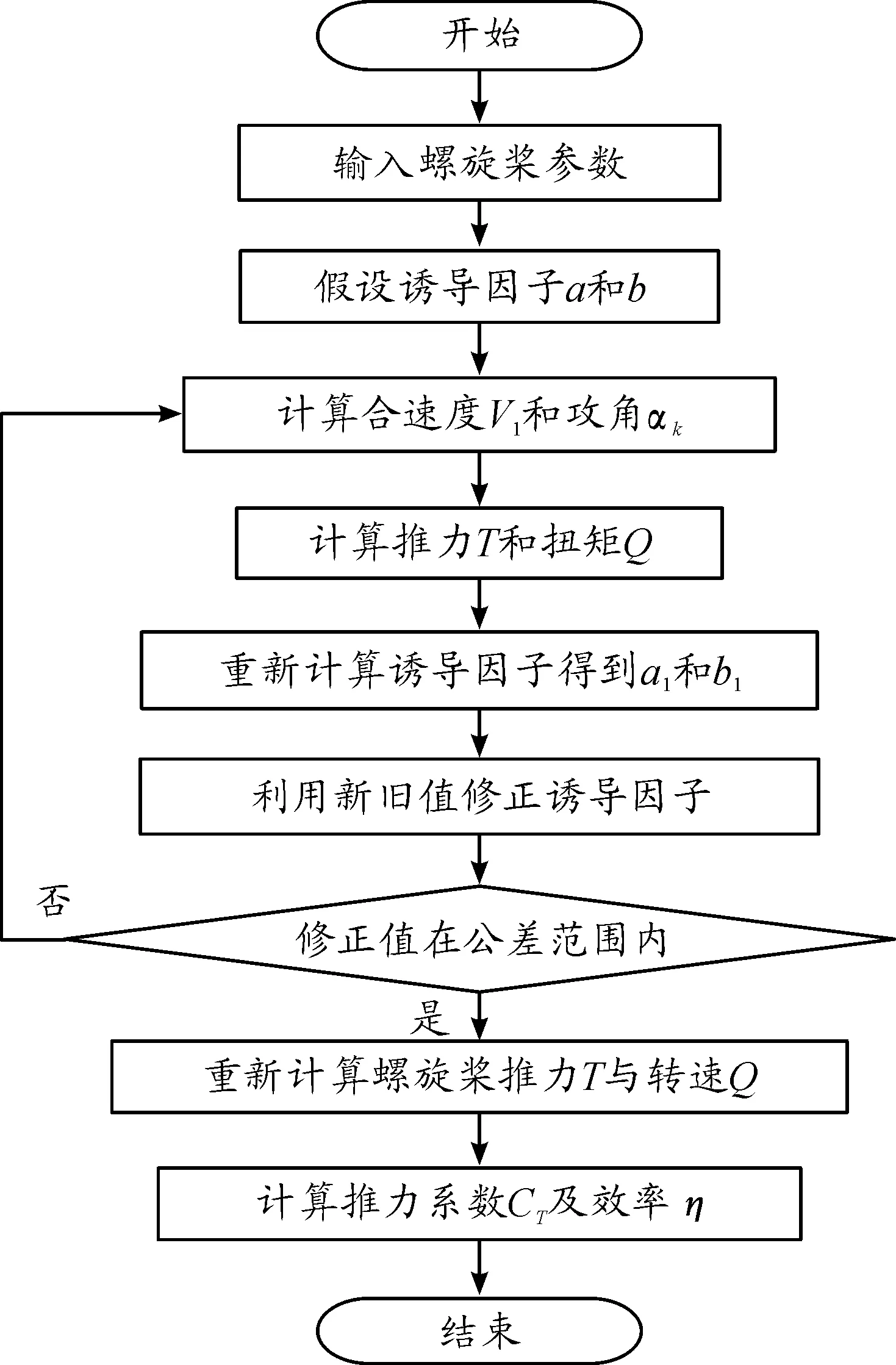
圖3 計算流程

1) 假設誘導因子a和b值并賦予初始值，利用式(8)和式(9)計算出流體的合速度V1和攻角αk；

2) 根據葉元體原理得出的式(6)和(7)，估計葉元體推力和轉矩；

3) 根據得出的推力與轉矩的近似值，利用動量守恒定理得出的式(15)和(17)，修正誘導因子a和b；

4) 重復1)至3)計算過程，使a和b的值在指定的收斂范圍內；

5) 賦予誘導因子a和b的收斂值，利用式(8)和(9)計算得到葉元體推力和轉矩的預測計算值。

2.2 相關計算參數

以某型號氣力推進艇螺旋槳葉片為研究對象，如圖4所示。螺旋槳葉片半徑為90 cm，其各半徑位置的弦長c和厚度h的數值如表1所示。

在計算中假定螺旋槳截面為相對簡單的標準線性化翼型設計及葉片具有恒定的螺距p。螺距p由標準螺距方程計算得到。

升力系數和阻力系數與槳葉的材料、形狀等因素有關，精確計算比較復雜，根據該螺旋槳的基本葉形，由Fluent軟件計算得到葉形在不同雷諾數和不同迎角下相對應的升力系數和阻力系數。經擬合數據得，升力系數CL和攻角αk略成線性關系，模型可取比例系數為6.2。

CL=6.2αk

(20)

阻力系數與升力系數的函數關系為：

(21)

P=2πrtanθ

(22)

圖4 槳葉實物

位置弦長c/mm厚度h/mmR8090.9R130140.8R163170.7R190230.6R213270.5R230330.4R234360.3R232350.2R210350.1R8034

2.3 螺旋槳推力計算結果

在氣力推進艇螺旋槳為2槳葉或3槳葉時，計算得到不同螺距角時的推力，如圖5所示。

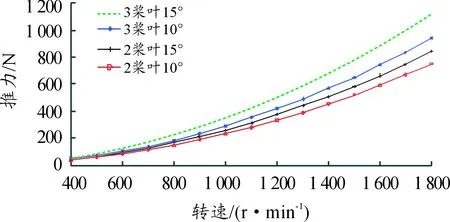
圖5 螺旋槳推力計算結果

3 螺旋槳推力測試試驗及結果分析

3.1 靜態推力測試方法

由氣力推進艇樣機、電子拉力計、聯接鋼絲繩、滾杠及固定樁等構成靜態推力測試系統，如圖6所示。氣力推進艇樣機選用4G63S4T增壓汽油發動機。發動機的最大功率是130 kW/5 000 r/min，最大轉矩是253 N·m/2 500 r/min。測試時將滾杠放置在平整、光滑的水磨石地面上，并將氣力推進艇安放在滾杠上，以盡可能地減小摩擦阻力。

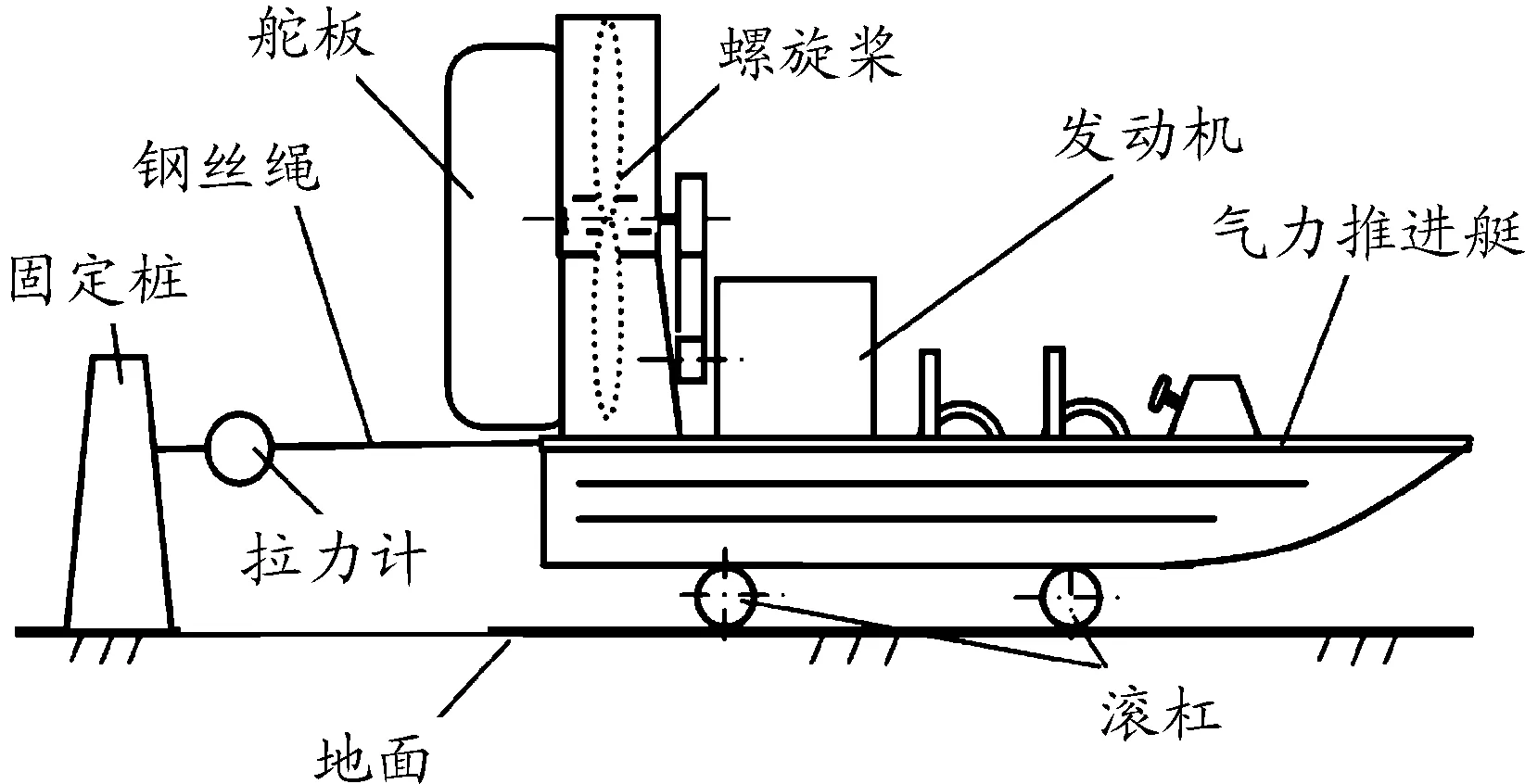
圖6 靜態推力測試系統

3.2 靜態推力測試結果

在螺距角不同時，3槳葉螺旋槳靜態推力測試結果，如表2、表3所示。

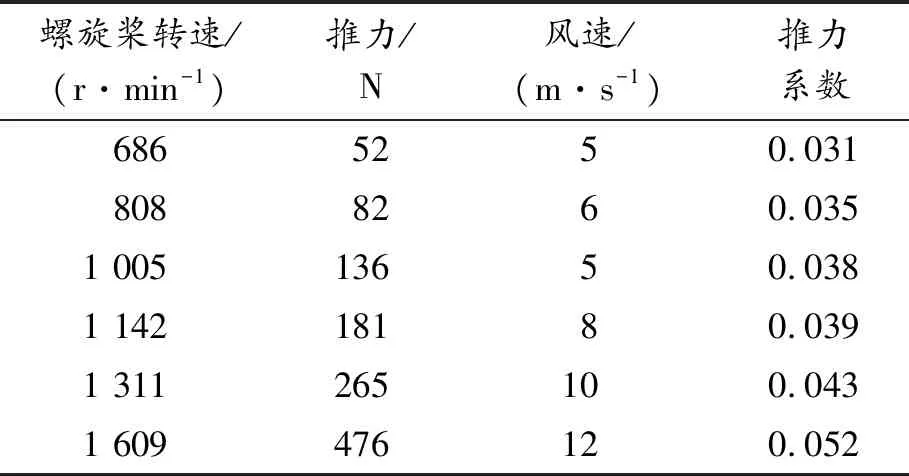
表2 螺距角10°時3槳葉靜態推力測試結果

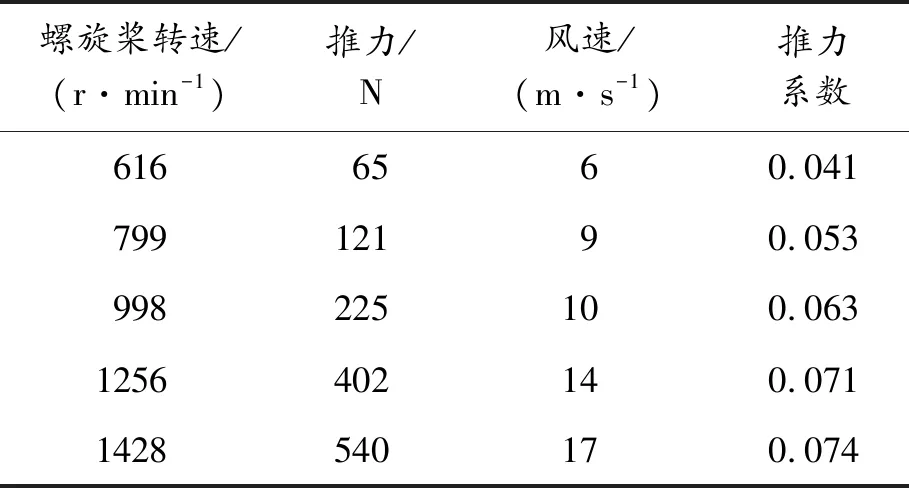
表3 螺距角15°時3槳葉靜態推力測試結果

在螺距角不同時，2槳葉螺旋槳靜態推力測試結果，如表4、表5所示。

表4 螺距角10°時2槳葉靜態推力測試結果

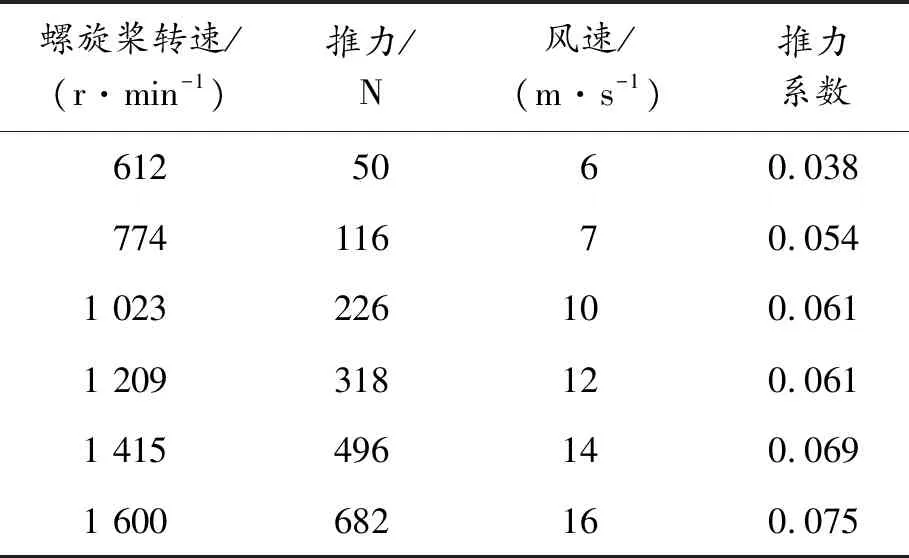
表5 螺距角15°時2槳葉靜態推力測試結果

3.3 螺距角不同時推力計算結果與檢測數據對比

螺距角不同時，3槳葉螺旋槳推力計算結果與測試數據的對比如圖7所示。可以看出，推力計算結果與測試數據都隨螺旋槳轉速的變化呈拋物線形。

相同螺旋槳轉速下，推力計算結果與測試數據的平均誤差見表6。螺距角相同時，3槳葉的推力計算結果與測試數據的平均誤差小于2槳葉；螺距角為15°時的推力計算結果與測試數據的平均誤差大于螺距角為10°時的誤差。

推力計算結果大于試驗檢測數據的原因主要是：在計算中采用的葉元體理論和動量守恒理論主要研究對象是理想螺旋槳，即假設空氣可以自由通過螺旋槳盤面，空氣速度和壓力在螺旋槳盤面上均勻分布，空氣為不可壓縮的理想流體以及螺旋槳截面為相對簡單的標準線性化翼型的影響。

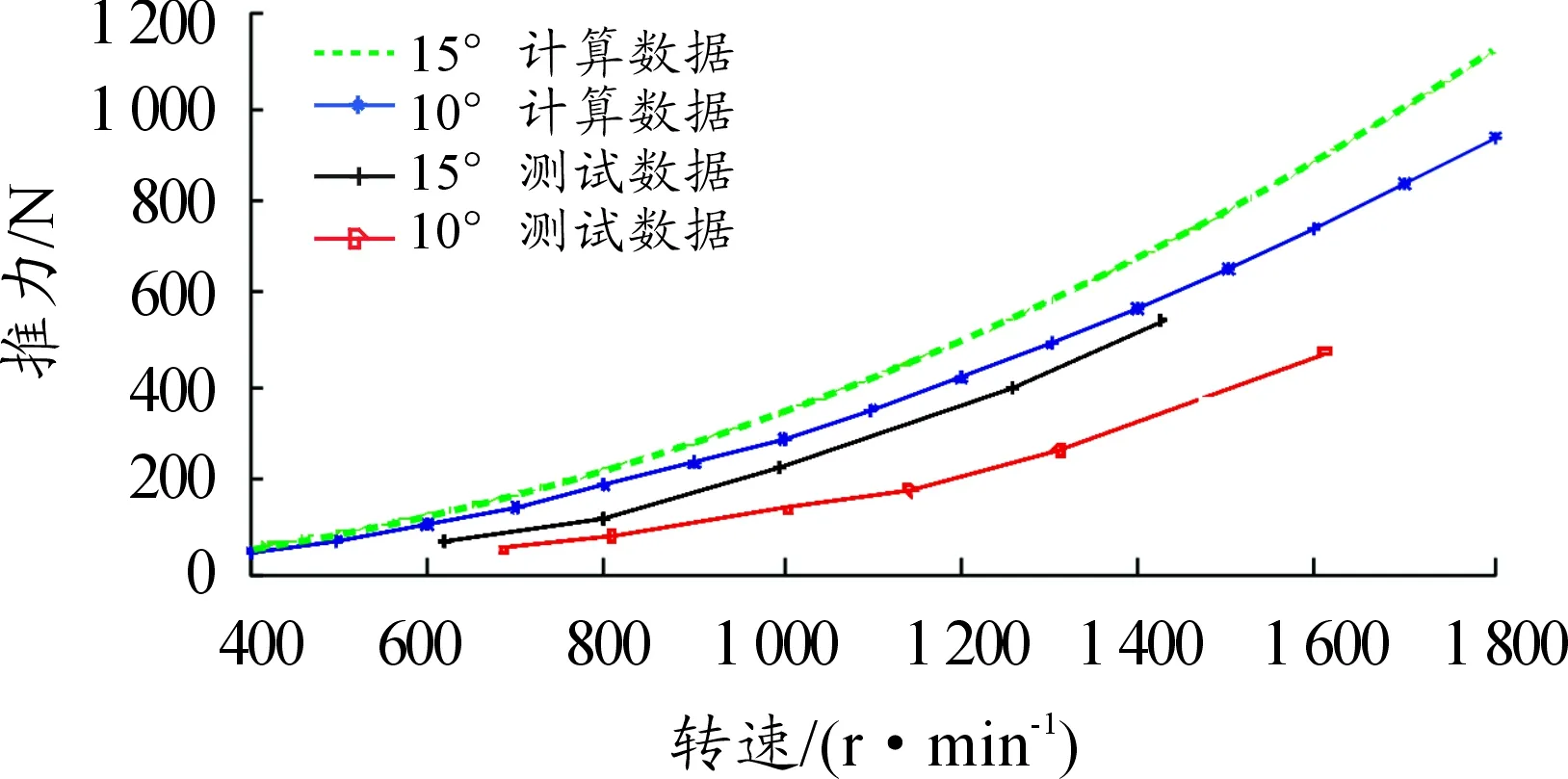
圖7 螺距角不同時推力計算與測試

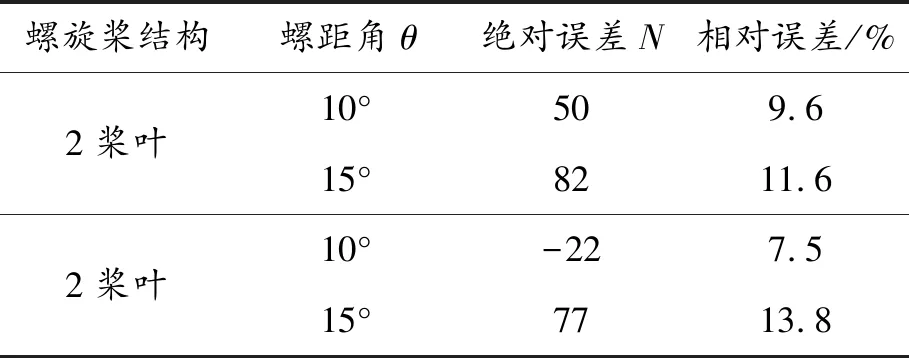
螺旋槳結構螺距角θ絕對誤差N相對誤差/%2槳葉10°509.615°8211.62槳葉10°-227.515°7713.8

3.4 槳葉數不同時推力計算結果與檢測數據對比

螺旋槳的槳葉數增多時，單位時間內流過螺旋槳盤面的流體質量增加，所以空氣單位時間內獲得的動量增加，即槳葉數多時推力也增加。在相同轉速下，3槳葉產生推力的計算結果比2槳葉的推力大，如圖8所示。但是，檢測獲得的不同槳葉數推力的增加幅度小于計算結果的增加幅度。但是，檢測獲得的不同槳葉數推力的增加幅度小于計算結果的增加幅度。這是因為螺旋槳數目增多后，槳葉之間的相互擾動變大，前一個螺旋槳槳葉的繞流會影響下一個螺旋槳槳葉周圍的流場分布，所以檢測獲得的不同槳葉數推力的增加幅度減小。

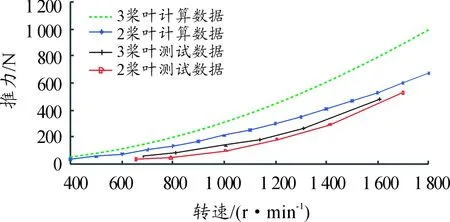
圖8 槳葉數不同時推力計算與測試結果

4 結論

1) 在螺距角和槳葉數不同時，螺旋槳推力計算結果與測試數據隨螺旋槳轉速的變化都呈拋物線形，即推力的計算結果與測試數據的變化規律相同，因此計算結果具有參考意義。

2) 在螺旋槳轉速、螺距角和槳葉數不同時,其平均絕對誤差有差異，最大平均誤差為87 N，相對誤差為10%～20%。

3) 螺旋槳推力計算結果與測試數據有差異的主要原因是計算公式的假設條件理想化及檢測試驗中存在著摩擦阻力等因素的影響。