玩轉方差 統計無憂
文
統計是初中數學中幾大主要板塊之一,其中“方差”是同學們最容易犯錯、最怵的統計知識點,究其原因是其計算量大,公式繁瑣。本文旨在幫助同學們剖析方差,厘清相關策略方法。當你能夠玩轉方差的時候,那你的統計無憂矣。
一、據方差性質解決問題
例1 下圖是甲、乙兩人在一次射擊訓練中擊中靶的情況(擊中靶中心的圓面為10環,靶中各數字表示該數所在圓環被擊中所得的環數),每人射擊了6次。
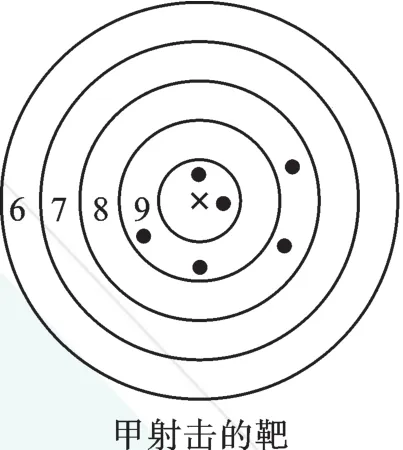
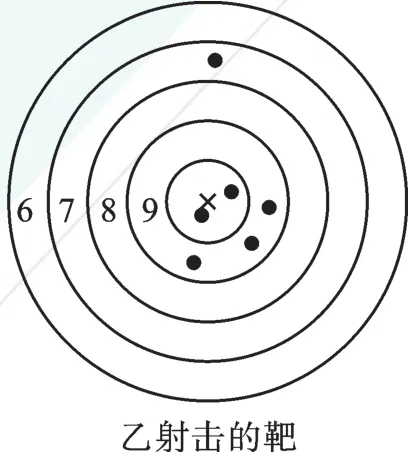
(1)請用列表法將他倆的射擊成績統計出來;
(2)若選派其中一人參賽,你認為應選哪人?請說明理由。
【解析】(1)根據兩人擊中靶的情況列表。
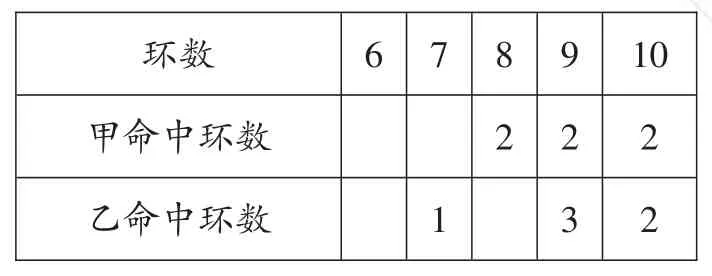
10 6 7 8 2環數甲命中環數乙命中環數1 9 2 3 2 2
(2)先求出兩人射擊成績的平均數,再求出兩人成績的方差<s2乙,可知甲與乙的平均成績相同,但甲發揮得比乙穩定,所以選甲參賽。
【點評】比較兩人的成績,首選平均數這個指標,平均數相當再選擇方差,因為方差反映了一組數據的波動大小,方差越大,波動性越大,方差越小,穩定性越好。
二、變化數據的方差概括
例2 一組數據a,b,c,d,e的方差是3,則新數據2a+7,2b+7,2c+7,2d+7,2e+7的方差是________________ 。
【解析】設一組數據a,b,c,d,e的平均數為m,則新數據2a+7、2b+7、2c+7、2d+7、2e+7的平均數為2m+7,方差為+7-2m-7)2+(2b+7-2m-7)2+(2c+7-2m-7)2+(2d+7-2m-7)2+(2e+7-2m-7)2]=4×[(a-m)2+(b-m)2+(c-m)2+(d-m)2+(em)2]=4×3=12。
【點評】將一組數據按照一定規則進行轉化,他們的平均數、方差是有章可循的。
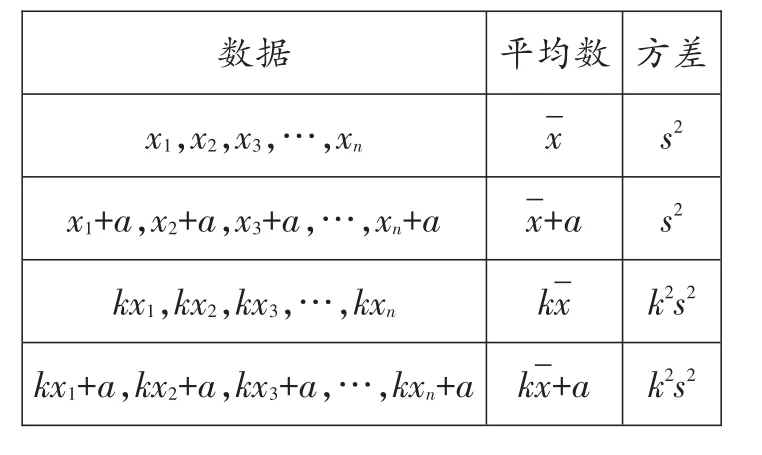
數據 平均數 方差x,x,x,…,xxs2 123n x+a,x+a,x+a,…,x+ax+as2 123n kx,kx,kx,…,kxkx k2s2 123n kx+a,kx+a,kx+a,…,kx+a kx+a k2s2 123n
三、運用整體思想求方差
例3 某學習小組5位同學參加初中畢業生實驗操作考試(滿分20分)的平均成績是16分。其中三位男生的方差為6(分2),兩位女生的成績分別為17分,15分。則這個學習小組5位同學考(a-16)2+(b-16)2+(c-16)2]=6,則(a-16)2+(b-16)2+(c-16)2=18,即可得這個學習小組5位同學考試分數的方差[(a-16)2+(b-16)2+(c-16)2+(17-16)2+(15-16)2]
【點評】由于不知道三位男生的成績,故無法直接求該小組成績的方差,先利用方程思想得到關于三位男生方差的方程,最后運用整體思想代入即可求解小組的方差。試分數的方差為________。

