異步電機矢量控制系統的仿真研究
李 瑾
(江西省精密驅動與控制重點實驗室南昌工程學院機械與電氣工程學院 江西南昌 330099)
1 前言
由于交流電機的數學模型是一個高階、非線性、強耦合的多變量系統,使對它的轉速控制不如直流電機那樣方便,通過將矢量控制技術用于異步電機的轉矩控制可使其調速性能夠跟直流電機相媲美[1][2]。
2 異步電機的數學模型
在靜止的兩相Oαβ坐標系下建立異步電機數學模型如下:
(1)電壓方程
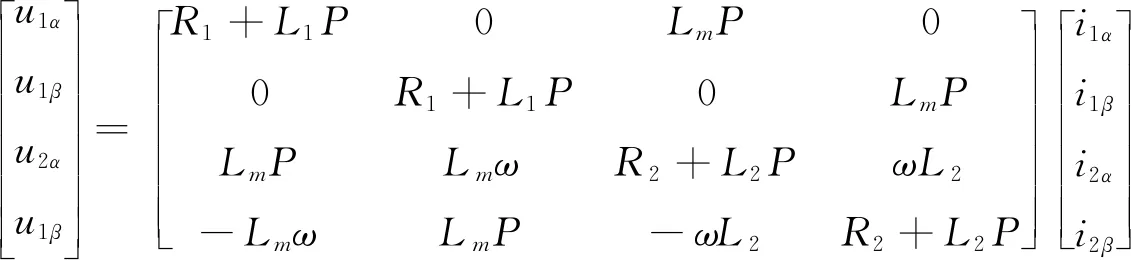
(1)
(2)磁鏈方程
(2)
(3) 轉矩方程
Tem=npLm(i2αi1β-i1αi2β)
(3)
以上三式中,下標中的1對應定子側、2對應轉子側的物理量,np為極對數,Lm為定轉子繞組的互感,ω為電機角速度。
3 矢量控制策略
本文采用定子磁鏈定向矢量控制,即將旋轉坐標的M軸定向于定子磁鏈Ψ1方向上,則定子磁通Ф1的T軸分量等于零。如果保持Ф1恒定,那么轉矩正比于T軸電流,這樣轉矩就直接等于兩個標量之積,能更好地實現對轉矩的控制[3]。另外采用定子磁鏈定向可使定子磁鏈觀測過程與轉子參數無關從而能夠簡化控制系統的結構。系統的矢量圖如圖1所示,其中MT坐標系以同步轉速ω1旋轉,dq坐標系以轉子轉速ω旋轉,α軸為坐標系旋轉的參考軸,則有θs=θ1-θ2=(ω1-ω)t為轉差角。

圖1 矢量圖
要實現定子磁鏈定向,需要定子磁鏈矢量的準確值,這里采用由檢測出的定子電壓和電流來計算定子磁鏈的U-I模型,圖2是U-I模型的結構框圖。
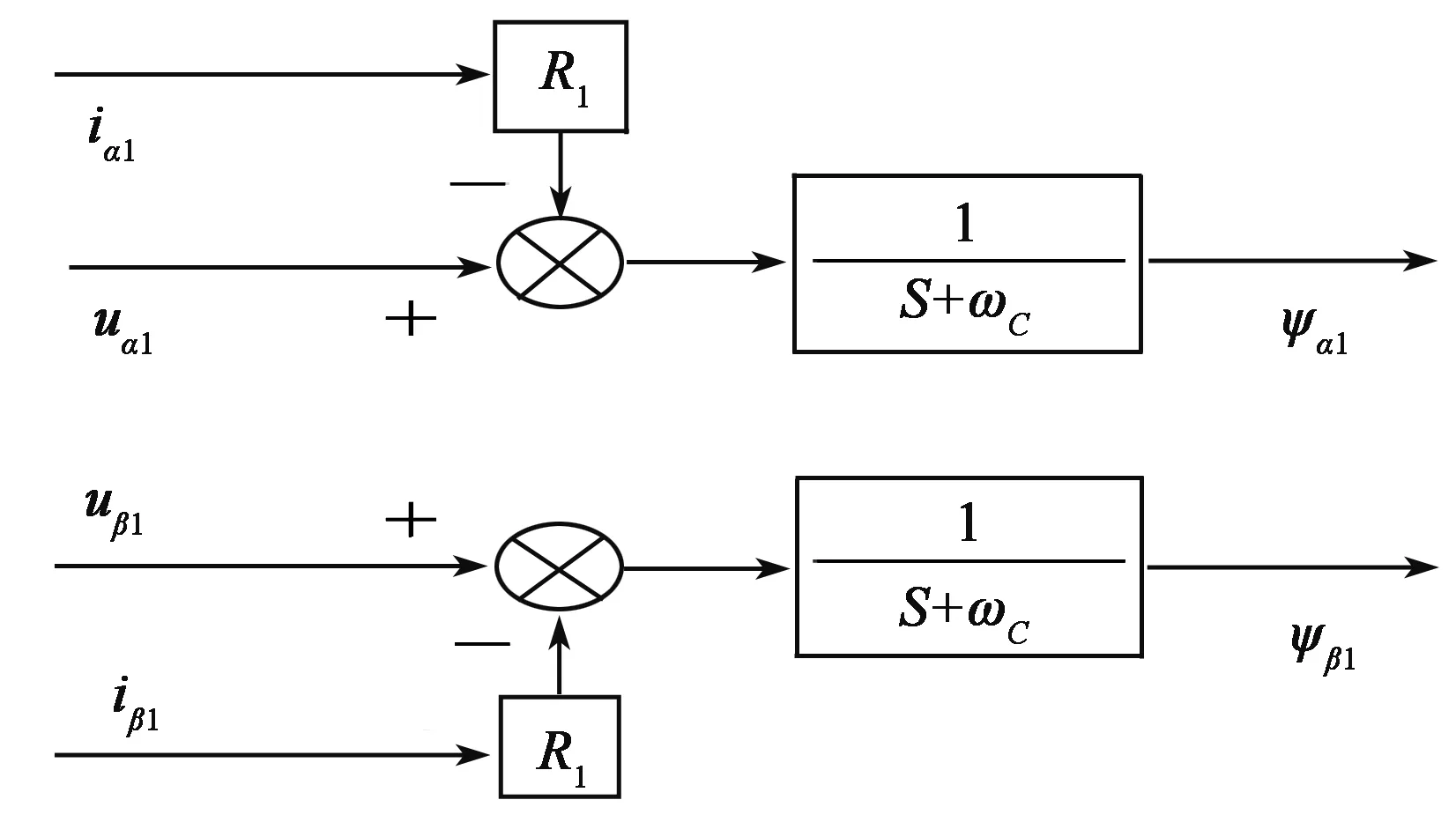
圖2 定子磁鏈的U-I模型結構框圖
4 坐標變換公式
(1)2/3變換
根據磁動勢等效,(4)式是由兩相Odq坐標系向三相Oabc坐標系(a軸與d軸重合)變換的公式(Odq坐標系與Oabc坐標系都以ωr速度旋轉,且三相繞組Y接法,無零線)。由圖1可得由以ωr速度旋轉的odq向靜止的oαβ坐標系及由以同步轉速ω1旋轉的OMT坐標系向靜止的oαβ坐標系轉換的公式分別如(5)(6)式所示:
(4)
(5)
(6)
由以上兩式有:
(7)
將(7)式代入(4)式有
(8)
(8)式即是由同步旋轉的OMT坐標系變換到以ωr速度旋轉的oabc坐標系的2/3變換(其中含旋轉變換)公式。
(2)3/2變換
由(4)式和(7)式可得:
(9)
(10)
由(9),(10)兩式可得由oabc坐標系變換到同步旋轉的OMT坐標系的3/2變換(其中含旋轉變換)公式。
(11)
5 系統仿真實驗
5.1 仿真框圖
運用MATLAB軟件對調速系統矢量變換部分進行仿真,得出仿真模型。
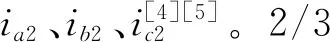
5.2 仿真波形
在仿真圖的基礎上對整個矢量控制系統進行建模仿真,電機參數設置如下:額定功率750W,額定電壓380V,額定轉速1420r/min,4極,功率因數0.86,效率84%。
初始給定轉速為1400r/min,t=0.2s時給定轉速值變為1000r/min,仿真得到的轉速波形如圖3所示。
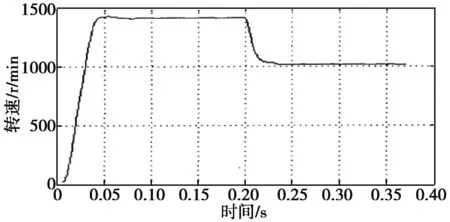
圖3 在0.2s轉速給定1000r/min時的轉速波形
從圖中可看出,當電機給定轉速值發生突變時,響應非常迅速,動態調整時間大約只有0.01s。
給定轉速1400r/min,電機空載起動,在0.2s時突加負載5N·m,得到的轉速和轉矩波形分別如圖4和圖5所示。
從圖4和圖5可見當突加負載時,電機的轉速和轉矩都能很快響應,t=0.2s時轉速經過短暫的動態調整之后迅速回復到給定值1400r/min,在t=0.2s時轉矩迅速上升,然后很快就穩定在負載轉矩值5N·m,響應非常迅速,說明系統的抗擾性能較強。
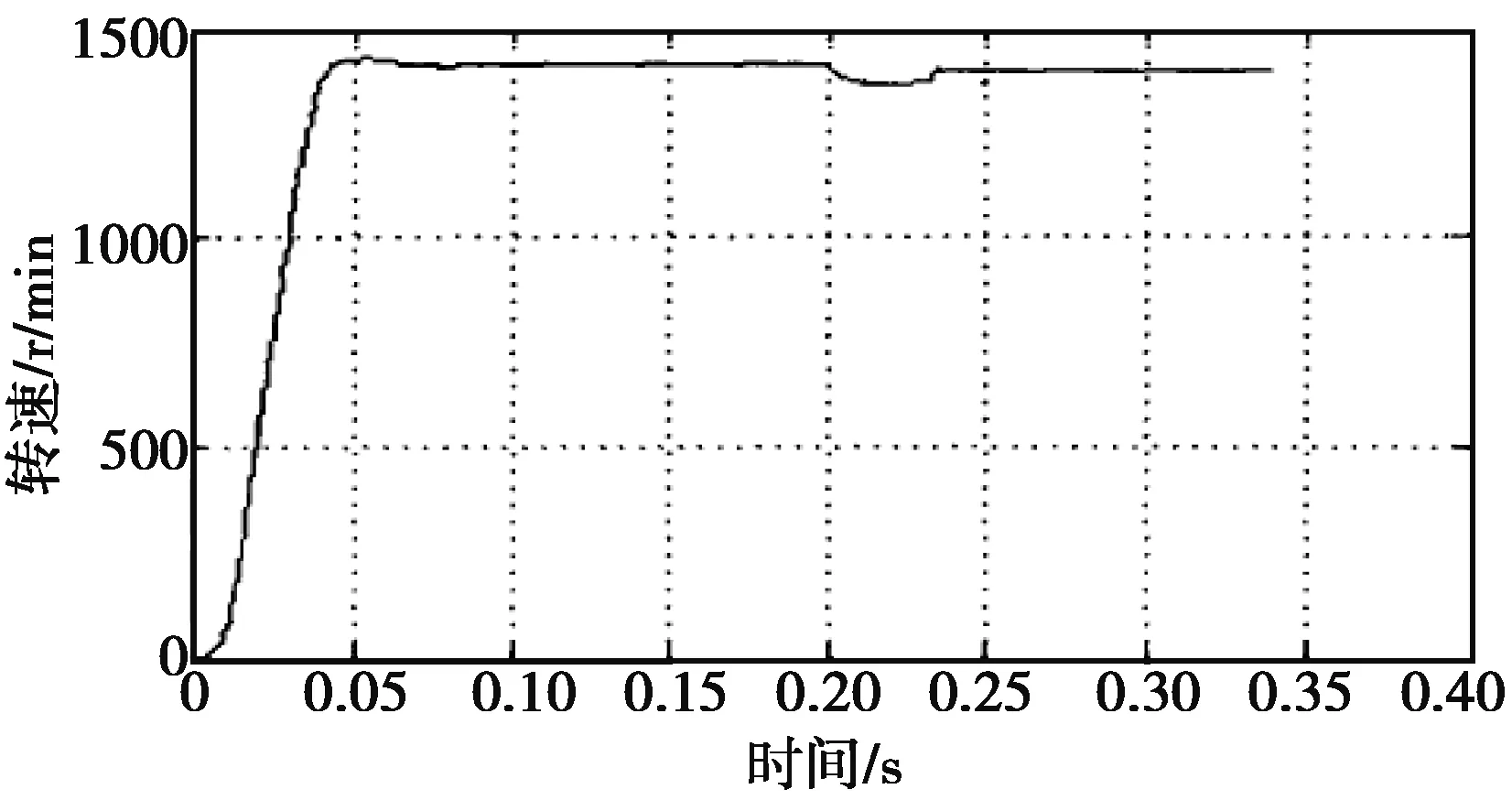
圖4 在0.2s突加負載時的轉速波形
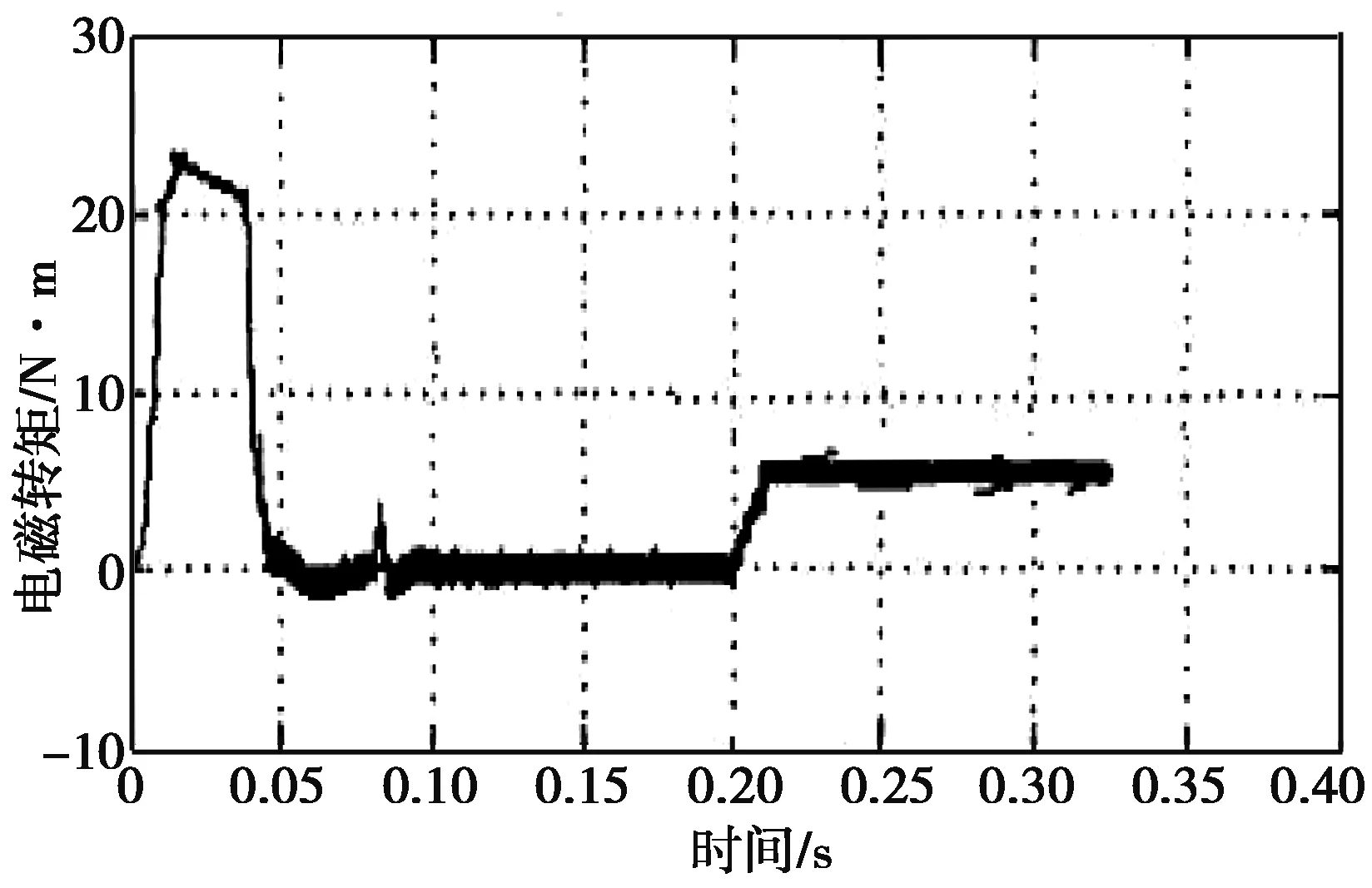
圖5 在0.2s突加負載時的轉矩波形
6 結論
本文分析了矢量控制原理,建立了采用定子磁鏈定向控制的異步電機矢量控制系統,對該系統進行仿真實驗的結果表明,采用本文所述的控制策略可使異步電機獲得完全能夠跟直流電機相媲美的調速性能。

