高階方向導數與乘積函數高階導數的形式一致性探討

張 騫 (隴東學院數學與統計學院，甘肅 慶陽 745000)

高階方向導數與乘積函數高階導數的形式一致性探討

張 騫 (隴東學院數學與統計學院，甘肅 慶陽 745000)

推導了乘積函數的高階導數和高階方向導數的計算，并對兩者進行比較，得出了其形式一致性的結果。

高階導數；方向導數；一致性

導數、高階導數、高階偏導數、方向導數[1-4]是微積分理論中很重要的知識點，其中高階導數的計算是一個難點，而對于高階方向導數更少涉及。為此，筆者主要給出了乘積函數高階導數的計算和高階方向導數的概念及計算，得到兩者的規律以及簡單表示方法。

1 乘積函數的高階導數

1.1f(x)g(x)的高階導數

設f(x)與g(x)分別為任意階可導函數，f(x)與g(x)可視為f(x)與g(x)的零階導數f(0)(x)與g(0)(x)，則：

[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)

[f(x)g(x)]″=f″(x)g(x)+2f′(x)g′(x)+f(x)g″(x)

[f(x)g(x)]?=f?(x)g(x)+3f″(x)g′(x)+3f′(x)g″(x)+f(x)g?(x)

利用數學歸納法可以得到f(x)g(x)的n階導數：

其形式與二項式(a+b)n的展開式相似，于是乘積函數f(x)g(x)的n階導數可以簡單表示為[f(x)+g(x)](n)。

1.2f(x)g(x)h(x)的高階導數

設f(x)、g(x)與h(x)分別為任意階可導函數，則:

(fgh)′=f′gh+fg′h+fgh′

(fgh)″=f″gh+fg″h+fgh″+2f′g′h+2f′gh′+2fg′h′

(fgh)?=f?gh+fg?h+fgh?+3f″g′h+3f′g″h+3f″gh′+3f′gh″+3fg″h′+3fg′h″+6f′g′h′

同理，利用數學歸納法可知f(x)g(x)h(x)的n階導數：

與三項式(a+b+c)n的展開式相似，于是乘積函數f(x)g(x)h(x)的n階導數可以簡單表示為[f(x)+g(x)+h(x)](n)。

1.3f1f2…fk的高階導數

依次類推可知乘積函數f1f2…fk的n階導數與(a1+a2+…+a3)n的展開式相似，于是乘積函數f1f2…fk的n階導數可以簡單表示為[f1+f2+…+f3](n)。

2 高階方向導數

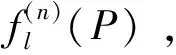
設函數f(x,y)在任意點P(x,y)存在所有二階連續偏導數，則f沿任一方向l的二階方向導數都存在，且：

式中，cosα，cosβ為方向l的方向余弦。可簡單表示為：

依次有：

+(fxxy(P)cos2α+2fxyy(P)cosαcosβ+fyyy(P)cos2β)cosβ

=fxxx(P)cos3α+3fxxy(P)cos2αcosβ+3fxyycosαcos2β+fyyy(P)cos3β

可表示為：

若f(x,y)存在n階連續偏導數，則：

推廣到三元函數的n階方向導數：

式中， cosα，cosβ, cosγ為方向l的方向余弦。

對于任意多元函數，也有：

式中， cosα1,cosα2,…,cosαk為方向l的方向余弦。

3 形式一致性

通過上述2類高階導數形式的比較，可以得到：

2)[f(x)g(x)]?與f?l(x,y)均相似于二項式(a+b)3的展開式。

可見，乘積函數的高階導數與高階方向導數具有形式一致性。

[1]華東師范大學數學系. 數學分析(上冊)[M] .第3版.北京：高等教育出版社，2001.

[2] 華東師范大學數學系. 數學分析(下冊)[M] .第3版.北京：高等教育出版社，2001.

[3] 劉玉璉.數學分析講義(上冊)[M].第4版.北京：高等教育出版社，2003.

[4] 劉玉璉.數學分析講義(下冊)[M].第4版.北京：高等教育出版社，2003.

[5] 張騫. 高階方向導數與多元Taylor定理的簡單形式[J]. 菏澤學院學報，2011(2)：11-13.

10.3969/j.issn.1673-1409(N).2012.09.002

O175.15

A

1673-1409(2012)09-N004-02

2012-06-16

張騫(1976-)，男， 2000年大學畢業，碩士，副教授，現主要從事非線性泛函分析和函數論方面的教學與研究工作。

[編輯] 洪云飛