不均勻進口總壓對渦輪氣動性能的影響

史文通，伊衛林，季路成

（北京理工大學機械與車輛學院1，宇航學院2：北京100081）

0 引言

航空發動機/燃氣輪機渦輪部件常依據進口參數均勻條件開展氣動設計[1-2]。隨著渦輪進口溫度提高和燃燒室結構復雜化，燃燒室稀釋氣、冷卻氣及主流氣摻混強烈，導致渦輪進口發生明顯的總溫畸變、總壓畸變及出現旋流現象，但其作用機理及影響規律尚不明晰。真實渦輪進口邊界條件對渦輪內流場分布影響研究越來越受到重視。在已有文獻中，渦輪進口總溫不均勻或熱斑相關研究較多，而對于渦輪進口總壓不均勻性影響的研究較少[3]。

2000 年和2002 年，Hermanson 與Thole 等[4-5]通過給定渦輪進口流速沿展高方向1 維分布，利用CFD 方法研究了進口總壓畸變對渦輪流場通道內影響，發現進口總壓分布直接影響渦輪流道內端壁區域的二次流發展；2007 年和2009 年，Barringer 等[6-7]在美國空軍實驗室渦輪研究平臺上，通過調節進口前燃燒室模擬器中的泄漏流和冷卻氣的溫度及流量，創造不同分布形式的渦輪進口邊界條件，發現不同進口總壓分布可使葉表局部靜壓負荷發生約10%的變化，同時對葉表靠近端壁區域的換熱系數也造成顯著影響；2017 年，Wang 等[8-9]通過數值研究指出當有進口總溫不均勻性條件存在時，進口總壓的不均勻性更直接影響渦輪流道內的熱流輸運與溫度分布。已有的研究表明：渦輪進口總壓分布不均勻對渦輪流場內的流動結構和熱負荷分布影響值得關注，但進口不均勻分布形式樣本往往較少，且進口總壓的不均勻性與總溫的不均勻性常相互耦合，所得出的結論具有一定局限性。

本文基于數值計算手段，分別以導葉和單級渦輪為研究對象，在總壓畸變高度δp和最大總壓畸變強度CPmax2 項特征因素的控制下對渦輪進口總壓展向1 維分布進行模化，以探究分布特征的變化對導葉及單級渦輪的氣動特性影響規律及進口總壓畸變環境下渦輪流道內的流動機理。

1 研究對象

本文選定的研究對象為NASA 高效節能發動機計劃中的GE-E3 發動機高壓渦輪，幾何數據來源于文獻[2]；數值方法校核算例參考試驗報告中的無冷卻環形葉柵試驗對計算域進行構建。數值校驗用計算域如圖1 所示。進口邊界P0的位置參考試驗的進口總壓測量平面，位于導葉（以下簡稱NGV）前緣前0.127 m。由于試驗的出口靜壓測量平面P1距離尾緣較近，僅為0.01016 m，為避免由此帶來的計算誤差，將計算域的出口平面位置向下游充分延長，至尾緣后0.127 m。

圖1 數值校驗用計算域

對于進口非均勻性對NGV 性能影響，進口邊界位置參考文獻[10-11]中對于渦輪與燃燒室交接平面（以下簡稱P40）的定義位置，選定NGV 前緣前40%軸向弦長處為不均勻分布的渦輪進口邊界條件的給定位置，相關網格亦做調整，保證不變。其計算域如圖2所示。

對于進口非均勻性對單級渦輪性能影響，計算域出口取在動葉尾緣充分距離之后的流道平直段，而出口監測面位于動葉尾緣后0.009525 m。其計算域如圖3 所示。

圖2 NGV 研究計算域

圖3 單級研究計算域

在上述2 個方面，對NGV 性能的評估指標采取試驗中使用的動能效率ηV，其定義為

式中：V1為出口面P1的實際速度；V1，isen為出口面P1的等熵速度；等效變換后，PS，1為P1面靜壓；PT，1為P1面總壓；PT，0為進口面P0的總壓；γ 為比熱容比，取1.4。

對1 級渦輪的性能評估指標，采用滯止等熵效率ηst，其定義為

式中：TT，2為P2處的總溫；TT，0為P40處的總溫；πT為P40面與P2面總壓的比值；k0為工質的比熱容比，取1.4。

2 研究方法

本文相關工作均基于數值方法開展，網格生成由ICEM 完成，數值模擬利用CFX 進行。首先將結合表1 所示工作條件，針對試驗數據進行校核。在計算中，工質選用理想氣體，來流方向均勻垂直于進口邊界平面且湍流強度為10%[12]。出口給定靜壓，滿足徑向平衡方程，參考位置為中展處。在后續研究過程中，除進口總壓邊界條件外，其余邊界條件的給定均與此相同，不再特別介紹。

表1 E3 發動機環形試驗邊界條件

2.1 網格無關性校驗

均保證固壁表面Y+＜1，分別生成67、130、192、252 萬4 套結構化網格，網格結構如圖4 所示。

在校核工況下4 種網格的計算結果見表2。從表中可見，監測參數隨著網格總數的增加變化較小，且趨于某一穩定值。

在0%和100%展高位置的絕熱Ma 對比如圖5所示。從圖中可見，隨著網格節點總數的增加，葉根和葉頂絕熱Ma 分布無明顯變化，且都與試驗值吻合較好。從上述對比可見，130 萬網格可滿足網格無關性要求，可用于后續研究工作。

圖5 不同網格數下葉根與葉頂絕熱Ma 對比

2.2 湍流模型的選擇

綜合考慮已有校核經驗[9，13-14]，使用γ-θ 轉捩模型應能進一步提高高壓渦輪氣熱模擬的準確性。本文參考試驗數據，對比了有/無（γ-θ）轉捩模型的SST 湍流模型對NGV“效率-壓比”和“流量-壓比”的計算差異。

計算結果如圖6 所示。當進口總壓與出口靜壓之比發生變化時，SST 模型與SST（γ-θ）模型在出口中展效率ηv和流量2 項計算結果的變化趨勢上具有高度的相似性。其中，對于中展效率的預測，當進口總壓與出口靜壓之比小于2.1 時，2 種模型都能較好地預測效率的變化趨勢，而數值上SST（γ-θ）模型的計算結果比SST 模型的更接近于試驗值；但當進口總壓與出口靜壓之比大于2.1 時，2 種模型都不能非常準確地預測出口中展效率。對于進出口流量的預測，在全壓比變化范圍內，2 種模型都能較好地模擬流量隨壓比的變化趨勢，且2 種模型計算結果的數值差異不大。對流場進行觀測發現，SST（γ-θ）模型對轉捩發生的軸向位置的預測比SST 模型的靠后，導致其計算得到的尾跡厚度比SST 模型的薄，因此，其計算得到的中展效率也高。

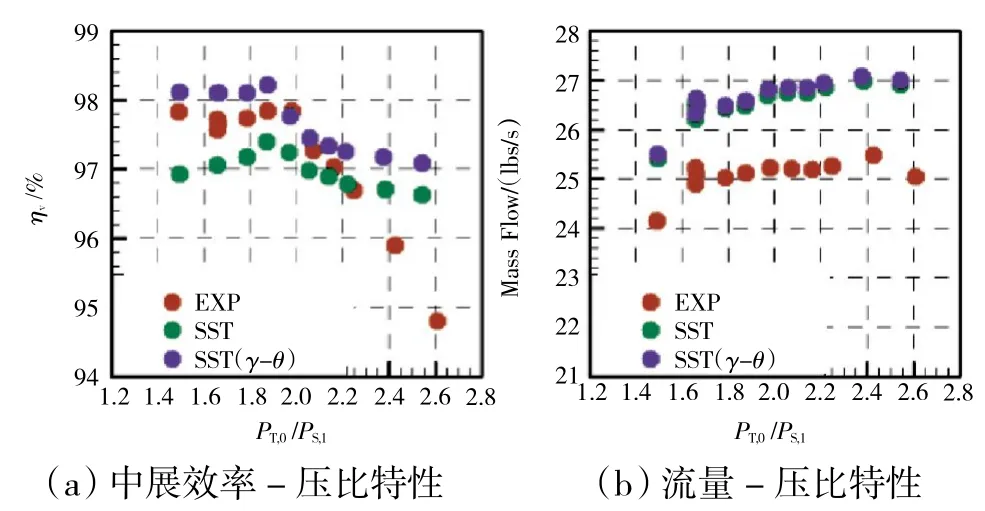
圖6 SST 與SST（γ-θ）2 種湍流模型的計算特性對比

出口總效率的預測對比見表3。當進口總壓與出口靜壓之比小于2 時，SST（γ-θ）模型計算結果與試驗值相比預測誤差更小，考慮到后續研究的展開主要基于設計工況（PT,0/PS,t=1.664），因此，后續的數值計算模型采用SST（γ-θ）模型。

表3 2 種湍流模型在不同壓比下出口總效率對比

2.3 進口總壓不均勻模化方法

文獻[6]給出了發動機真實燃燒室及多種燃燒室模擬器的出口總壓沿展高方向分布的試驗數據，如圖7 所示。從圖中可見，總壓分布具有靠近中展區域均勻，而在靠近端壁區域從某一展高開始平滑過渡到端壁表面某一極值的特征。

圖7 真實燃燒室出口總壓分布

因此，本文參考這種分布規律，將其簡化為對稱分布形式，如圖8 所示。從總壓畸變發生位置到端壁的總壓極值點，使用拋物線公式過渡。在總壓畸變高度δP和最大總壓畸變強度CPmax2 種變量的控制下，可以獲得任意的總壓分布。其中，最大總壓畸變強度CPmax表示在端區位置處的總壓畸變的極值。δP為進口邊界總壓畸變發生位置距離端壁的距離與進口截面展高的比值。當地總壓畸變強度CP用來描述當地總壓與中展處總壓的差異，即

式中：P 為當地總壓；PMS1為渦輪進口中展處總壓；1/2ρAVEU2AVE|1為均勻進口邊界條件下渦輪進口處平均動壓。

參考真實情況，本文選定的δP變化范圍為[0，40%]，CPmax的變化范圍為[-2，+2]，并分別根據這2種分布特征對NGV 和單級渦輪的氣動損失帶來的影響進行數值研究。具體方法為，限定δP=30%不變，給定Cpmax={-2，-1.5-1-0.5 0+0.5+1+1.5+2}的進口總壓分布條件，以探究總壓畸變強度對下游流場的影響；限定|CPmax|=2 不變，給定δP={10%，20%，30%，40%}的進口總壓分布條件，以探究總壓畸變高度對下游流場的影響。2 個參數變化帶來的進口分布變化如圖9 所示。

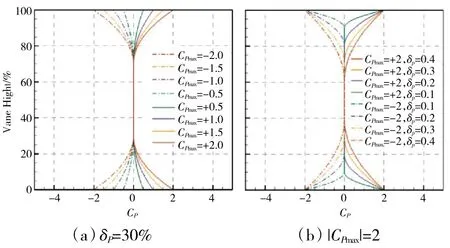
圖9 非均勻進口總壓分布

3 進口總壓不均勻對效率的影響

3.1 NGV效率影響

將如圖9 所示的不同進口邊界條件施加于如圖2 所示的計算域。不同進口條件對于NGV 效率的影響如圖10 所示。

圖10 總壓畸變對NGV 效率的影響

從圖10（a）中可見，當δP相同時，CPmax對ηV有影響，但正/負2 種畸變的影響卻不相同。當CPmax＞0 時，ηV隨CPmax的增大而快速線性降低，影響幅度可達0.5%；當Cpmax＜0時，ηV隨CPmax絕對值的增大而先快速提高后緩慢降低，但幅度很小，最大影響幅度僅為0.18%。總體來說，當總壓畸變為負時，ηV有所提高，但效果不明顯；當總壓畸變為正時，ηV降低且效果顯著，值得進一步深入探討。

從圖10（b）中可見，當CPmax不變時，若CPmax＞0，相比于均勻進口總壓邊界條件，非均勻進口條件會使顯著降低，影響幅度可達0.5%。但δP＞10%后，隨著δP的增大，ηV變化不明顯。若CPmax＜0，δP的變化對ηV的影響不明顯。

在上文各模擬條件中，總壓徑向分布形式發生了改變，因而總壓平均值也發生變化。為了進一步分析是否因進口總壓平均值的變化影響ηV，本文還對與各總壓畸變情況進口總壓流量平均值相同的均勻進口總壓邊界情況進行計算。結果顯示基本無變化，因此，可見ηV的變化主要來自于端區總壓變化造成的流道內流場結構改變。

3.2 單級渦輪效率影響

將如圖9 所示的不同進口邊界條件施加于如圖3 所示的計算域。不同進口條件對于單級高壓渦輪的滯止等熵效率的影響如圖11 所示。

從圖中可見，2 種總壓畸變特征的變化對渦輪級效率的影響規律與對NGV 的影響規律幾乎一致。當CPmax＞0 時，CPmax和δP的ηSI變化對的影響幅值分別為0.58%和0.59%；當CPmax＜0 時，CPmax和δP的變化對ηSI影響的最大幅值為0.07%和0.06%。

圖11 總壓畸變對單級效率的影響

同樣的，經計算發現，隨進口總壓分布變化產生的進口總壓平均值的變化對于ηSI的影響幅度非常微小，可以忽略不計。

4 內部流場分析

4.1 NGV內流場分析

4.1.1 CPmax＞0

P1面經整體流量平均后的NGV 效率沿展高分布如圖12 所示。從圖中可見，與均勻進口條件相比，當CPmax＞0 時，在10%展高以下和80%展高以上的效率有所升高，而在中展區域效率有所降低。并且隨CPmax的增大，這一特征越來越明顯。

圖12 CPmax 對ηV 的影響

圖13 效率監測面上的ηV 分布

選擇變化強度最大的CPmax=+2 工況開展進一步研究，將其在P1面上的與均勻進口條件得到的ηV分布進行差運算，如圖13所示。從圖中可見，2 個高效區A 和C 與1 個大低效區B 的存在，從展向分布上看與圖12 的吻合。

對高效區A 的射入流線進行監測，如圖14 所示。從圖中可見，對于CPmax=+2 的情形，A 區的氣體主要由通道中間的氣體發展而來，而對于均勻進口條件情形，A 區的氣體是流經葉片壁面附近發展而來的。相比之下，在CPmax=+2 時，氣體更少流經近壁面區域，也沒有發生大的渦流與卷曲，保持了入口處的高總壓特征，因此效率更高。

圖14 A 區回溯流線

同樣的，對高效區C 的流線進行回溯，如圖15所示。從圖中可見，在均勻進口條件下，C 區的流體曾受到橫向二次流的作用撞擊到葉片吸力面。而在時，端區流體的總壓更高，橫向二次流效應減弱，流線未經撞壁，更為平直的射入了C 區，因此損失更小，使C 區的效率更高。

圖15 C 區回溯流線

低效區B 由3 個低效核心區B1、B2和B3組成。對這3 個低效區的流線進行回溯發現，B1區的流體主要來自于貼近葉片壓力面流動的流體，B2和B3區的流體主要來自于貼近葉片吸力面流動的流體。進口靠近端壁區域的流體受進口總壓梯度的作用向中展區域匯集，經過撞擊與摻混后流至B1區，而在均勻進口條件下，B1區的流體由進口處同展高的流體平順發展而來，如圖16 所示。從圖中可見，流線先通過的云圖1 為渦量云圖，從該云圖中可見，在CPmax=+2 時，端區流體向中心匯聚的過程中產生較強的渦流，由此發生動能損失，使最終匯集到的B1區流體的效率低于均勻進口條件下的效率。

相比于均勻進口條件，在CPmax=+2 時，B2和B3區回溯流體在進口面的展向分布范圍更大，如圖17 所示。這同樣是由于受到端區總壓梯度的作用，而使流線向中展區域匯集。

圖16 B1 區回溯流線

圖17 B2 和B3 區回溯流線

但與圖16 相比，其匯集作用并沒有流經壓力面的流體所受到的那樣強，流線相對平直，無明顯旋流產生，因此，更多的損失應由其他因素造成。B2區所處展高位置約56.5%，繪制該展高位置葉片吸力面上的形狀因子分布如圖18（a）所示。從圖中可見，無論是均勻進口分布還是CPmax=+2 的情況，延流向發展，形狀因子都存在由高到低的跳躍過程，通常這一過程由轉捩流動導致[15]。但明顯可見，在CPmax=+2 時，形狀因子跳躍過程發生的位置更加提前，所占軸向距離也更短。說明在CPmax=+2 時，轉捩發生得更快且位置更加提前。葉片表面湍動能分布中也能較好地觀測到這一現象，如圖19 所示。從圖18（b）中可見，在CPmax=+2時，轉捩后附面層更厚。附面層內流體速度和總壓明顯低于主流區的，因此當附面層增厚時，尾跡中的高損失區增厚，這也是低效區B2產生的原因。推論低效區B3由同樣的理由產生。

圖18 吸力面56.5%展高處的形狀因子與附面層厚度

圖19 葉片表面湍動能分布

結合圖12 與13 可見，在CPmax＞0 時，使出口動能效率降低的主要因素是B1區的產生，亦即受進口總壓梯度影響的壓力面流體向中展區的匯集與碰撞。在δP相同時，CPmax越大，匯集與碰撞的強度越大，因此損失增大，ηV線性降低；而在CPmax相同時，δP越大，匯集點越提前，如圖20 所示。但δP足夠大時，匯集點進一步提前不能引起匯集點后更多流動形式的改變，因此δP的增大沒有使ηV線性降低。

圖20 不同δP 情況滯止點前釋放的流線（CPmax=+2）

4.1.2 CPmax＜0

觀察圖10 可見，在CPmax＜0 時，相比于均勻進口條件，ηV變化不顯著，僅略有微量提高。從圖12（b）中可見，中展區的整體流量平均效率有明顯提高，而端區的效率則明顯降低，綜合來看整體積分面積變化不大，這與圖10 得到的結論是相對應的。為進一步理解其原因，做NGV 效率監測面各展高的流量平均效率分布和流量分布隨CPmax的變化曲線，如圖21 所示（δP=30%）。從圖中可見，在CPmax＜0 時，上、下端區各成對出現1 組流量平均效率的高低極值區，但變化幅值較小。從圖21（b）可見，與之相比更為顯著的，在時，中展區的流量增加，端區流量降低，同時隨CPmax絕對值的增大，流量進一步向中展區集中。當取出口面整體流量平均時，在圖21（b）中各展高流量的大小相當于圖21（a）中各展高流量平均效率的權值，因此盡管端區流量平均效率有所變化，但在CPmax＜0 時，對流量分布帶來的影響更為顯著，中展區域高動能效率流體流量比重的增大，在CPmax＜0 時，整體流量平均效率沒有降低甚至有微量提高的原因。

圖21 在CPmax＜0 時流量平均效率與流量沿展高的分布

圖22 經過P40 面不同展高扇面的流線及P1 面帶流量比重的效率分布

在3 維流場中，從進口面90%～100%和70%～80%展高的環形面釋放流線，對在CPmax=-2（CP=30%）的情況與均勻進口情況進行觀測，如圖22（a）所示。其中藍色流線由90%～100%展高的環面釋放，紅色流線由70%～80%展高的環面釋放。如圖22（b）所示的云圖為對應情況出口面的ρ*Vw分布，以作為流量分布的參考。對于從2 種不同展高范圍出發的流體，都可看作2 部分，一部分的出發位置更靠近吸力面，另一部分則更靠近壓力面。在CPmax時，靠近吸力面的流體流速較高，受進口徑向總壓梯度的作用效果不顯著，仍保持較為平直的流線貼近吸力面流動。而靠近壓力面的流體流速較低，受到進口徑向總壓梯度作用后效果顯著。對于從進口90%～100%展高出發的流體，其總壓較低，在總壓梯度作用下向端壁遷∑，撞壁后回流并在靠近進口的區域滾動，最終受橫向靜壓差的作用匯入靠近吸力面流動的高速流體。對于從進口70%～80%展高出發的流體，其總壓較高，在總壓梯度的作用下，向更高的展高區域流動擴張而未回流，最終占據貼近壓力面流動的70%～100%展高的區域，如圖23 所示。而這些流體在通過流道時受到橫向靜壓梯度的作用，向吸力面遷∑，并擠占靠近吸立面流動的高展高區域。這部分來自進口靠近壓力面位置的流體的流速較低，總壓較高，因此最終出口面的高展高區流量減小，原本貼近吸力面高展高區流動的流體被擠壓至更低展高區域，使得出口面稍低于機匣的展高區出現了流量匯集。對靠近輪轂的展高區有類似現象，不再贅述。

圖23 紅色流線橫向流動，擠占了吸力面高展高區

當δP不變，CPmax絕對值增大時，這種擠占和流量匯集的趨勢更加顯著，因此出現了如圖12（b）所示的出口效率分布變化。而根據圖10（b）所示，出口總效率隨δP的變化不明顯，說明CPmax不變時，δP的變化不會使流動狀況發生顯著改變，在此不再深入討論。

4.2 渦輪級內流場分析

4.2.1 CPmax＞0

作CPmax=-2（δP=30%）時動葉流道內高損失區的云圖，如圖25 所示。其中高損失區定義為ΔηSI·ρ·VW＜0。從圖13 中可見，在CPmax＞0 時，靜葉出口形成的流體動能損失較高的B，在流入旋轉的動葉流道后形成周向全環形的高損失帶。又如圖24（a）所示，作通過動葉進口高損失帶的流線，靜葉流道內向中心區匯集的流體在進入動葉流道后以較為平順的趨勢通過了流道。靜葉流道出口的流動情況較為平順地傳遞到動葉流道出口，因此在CPmax＞0時，ηSI隨CPmax和δP的變化規律與對靜葉流道的相似。

圖24 經過中展高損失帶的單級內流線

圖25 在CPmax=+2 時動葉內流道高損失區的分布

4.2.2 CPmax＜0

相似的，做在CPmax=-2（δP=30%）時動葉流道內高損失區的云圖，如圖26 所示。靜葉出口的高損失區在動葉前形成高損失帶，其位置集中于上下端壁附近。做通過這2 個高損失帶的流線如圖27 所示，可見動葉出口的高損失帶分布與這些流線在動葉出口通過的位置有對應關系。

因此在CPmax＜0 時，ηSI隨CPmax和δP的變化規律與靜葉流道的相似。

圖27 經過端區高損失帶的單級內流線

5 結論

本文針對渦輪進口總壓沿展高方向1 維分布的不均勻性，利用總壓畸變高度δP和最大總壓畸變強度CPmax2 項特征因素對其進行模化，開展了不同總壓畸變形式對GE-E3 發動機高壓渦輪第1 級導葉和第1 級氣動性能影響的數值研究，得到以下結論：

（1）當渦輪進口端區總壓高于中展區總壓時，導葉出口效率顯著降低。這主要由靠近壓力面流體向中展區的匯集碰撞以及靠近吸力面的流體提前發生轉捩流動導致。隨畸變強度的增大，導葉出口效率線性降低，幅值可達0.5%。畸變高度的增大，會使匯集位置進一步提前。

（2）當渦輪進口端區總壓高于中展區總壓時，導葉出口中展區流量增加，端區流量減少，各展高的流量平均效率變化不大，整體平均后，進口總壓畸變形式的變化對導葉出口氣動效率影響不明顯。

（3）從定常解來看，靜葉出口的參數分布較為平直地傳遞到動葉出口，因此，總壓畸變對第1 級渦輪氣動性能的影響規律與對第1 級導葉的相似。進口總壓畸變引發的渦輪級絕熱效率降低幅值可達0.59%。

盡管本文所選的型號樣本和工況樣本具有一定的局限性，但仍可見在渦輪設計過程中，不均勻的進口總壓邊界條件值得關注和進一步研究。

圖26 在CPmax=-2 時動葉內流道高損失區的分布