基于GTWR的武漢市房價預測
龐博
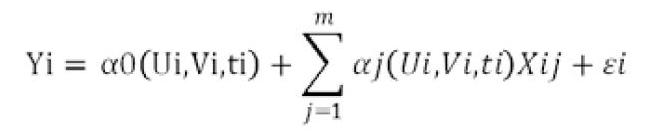
【摘 要】 城市住房價格一直是社會關注度最高的熱點問題之一,其關系到每一個公民的切身利益。而地理加權回歸(GWR)模型不能有效處理樣本數據時空相關性這一問題,利用GTWR模型有效地將時空數據進行結合,并對武漢市的房價進行分析。有效解決了地理加權回歸模型的不足。研究結果表明,各個因子對住宅價格所起的影響不同。GTWR在GWR的基礎上,進一步把握了不同因子在時間上對住房價格影響的差異性,進而能夠提供不同時間不同地點的住房價格分析和輔助決策支持。
【關鍵詞】 GTWR 住房價格 時空數據
1.研究方法
1.1 GWR模型
地理加權回歸(GWR)模型是一種空間分析模型。在空間分析中,觀測數據一般按照給定的地理位置作為采樣單元進行采樣,隨著地理位置的變化,變量間的關系或者結構會發生改變,即GIS中所說的“空間非平穩性”。這種空間非平穩性普遍存在于空間數據中,如果采用傳統的線性回歸模型來分析空間數據,一般很難得到令人滿意的結果,而利用GWR模型,通過建立空間范圍內每個點處的局部回歸方程,來應對空間數據自身的這種屬性,其在探索變量間空間變化關系及對未來結果預測過程中具備明顯優勢。
1.2 GWR模型的改進—GTWR模型
GWR利用空間變化的回歸系數進行擬合估測,并未直接考慮空間依賴性,模型殘差ε具有不確定性,可能包含部分能夠建模的時空相關性。GTWR是在GWR模型的基礎上,將空間位置坐標和時間序列坐標構成三維坐標,同時考慮空間和時間對各解釋變量的回歸系數的影響。時空坐標系中,時空位置i的坐標為(Ui,Vi,ti), GTWR模型為:
Yi作為樣本點i的被解釋變量值,n為樣本點的數目,m為解釋變量的數目,ti為第二個樣本點的時間坐標;α0(ui,vi,ti)表示樣本點i的時空截距;Xij表示樣本點i的第j個解釋變量值;αj(ui,vi,ti)表示樣本點i處第j個變量的回歸系數,是時空坐標的函數;表示殘差。時空權重函數wi(ui,vi,ti)=wi(ui,vi) wi(ti),其中wi(ui,vi) 是空間權重,wi(ti) 為時間權重。計算時空距離時,可乘以參數λ作為時空權重的平衡因子。因將時空三維坐標引入模型,GTWR能提高模型擬合精度,且從時空三維角度提供各解釋變量對因變量的影響分析,具有比較好的解釋力。
2 研究區域及數據
本文選取湖北省武漢市作為研究區,武漢地處江漢平原東部、長江中游,是武漢城市圈的中心城市。全市面積8494.41平方公里。研究數據集共選取東湖高新區、蔡甸區、東西湖區、沌口、漢南區、漢陽區、洪山區、黃陂區、新洲區、江岸區、江漢區、江夏區、硚口區、青山區、武昌區十五個區共43272個數據作為樣本點。為便于作整體分析,按樓棟計算平均住房單價,研究區域樣本住房呈非均勻分布,針對樣本數據進行相關分析,發現價格與綠化率、商業條件、醫療條件、休閑娛樂、交通狀況呈現或強或弱的線性相關關系。
3 數據處理
選擇價格解釋變量:反映社區環境的綠化率,反映城市區位屬性的商業條件、醫療條件和休閑娛樂條件,反映宏觀經濟政策和政策變化的銷售年份,以及反映交通通達度的交通狀況。其中,銷售年份以2017年為基準,轉化為年度索引值。之后對其進行歸一化處理,并進行主成成分分析。
4實驗過程
基于此,利用SPSS對數據進行主成分分析,得到結果,可以得到各因素的權重。通過KMO和Bartlett檢驗,可以得到取樣足夠度的 Kaiser-Meyer-Olkin 度量為0.778,適合主成分分析的程度為“一般”,基本可以用主成分分析求得權重。既而后求得載荷數,得到各因子的權重和相關的指標信息。
GTWR的模型分析結果,見下表。其模型的擬合度R2為42.92%,AICc為73332.9,綜合來看,研究區域的房價整體上與商業、醫療、休閑娛樂、交通等因素呈現出正相關性。這些反映出了區位因素和環境因素對住房價格的影響。
5 結論
針對地理加權回歸(GWR)模型不能有效處理樣本數據時空相關性這一問題,利用GTWR模型有效地將時空數據進行結合,并對武漢市的房價進行分析。有效解決了地理加權回歸模型的不足,并未時空一體化研究提供了道路。研究結果表明,對于城市住宅區價格而言,其與綠化率、商業條件、醫療條件、休閑娛樂、交通狀況、時間因素等呈現出相關性,各個因子對住宅價格所起的影響也是不同的。GTWR在GWR的基礎上,進一步把握了不同因子在時間上對住房價格影響的差異性,進而能夠提供不同時間不同地點的住房價格分析,對于我們選購住房、預測房價具有很強的現實意義。也能為政策制定者提供更準確、細致的分析和輔助決策支持,達到促進房地產產業健康發展的目的。
【參考文獻】
[1] Brunsdon C,Fotheringham A.S and Charlton M., 1996. Geographically weighted regression: a method for exploring spatial non-stationarity, Geographical Analysis 28, 281-298.

