頁巖地層的破裂壓力地震預測方法

馬 妮,林正良,胡華鋒,周 單,王世星

(中國石油化工股份有限公司石油物探技術研究院,江蘇南京211103)

在油氣勘探開發過程中,會遇到許多與鉆井、測井、壓裂等方面密切相關的實際工程問題。這些問題復雜多變,是油氣藏巖石力學性質研究的重點和難點,內容涉及井壁穩定性、地應力、地層孔隙壓力、巖石的力學性質、地層巖石可壓裂性、地層的破裂壓力與坍塌壓力等方面[1]。其中地層破裂壓力的有效預測可為井壁穩定性、合理水力壓裂設計、油層改造方案和安全鉆井方案等提供可靠的依據。

地層的破裂壓力定義為井壁受到拉伸破壞時所承受的臨界井眼壓力[1]。現階段獲取地層破裂壓力的方法主要有室內巖樣破裂試驗和測井資料估算。通過室內巖樣實驗得到地層破裂壓力是最為直接、有效的手段,但該方法所能獲取的數據有限,且不具有連續性。而利用測井資料計算破裂壓力的方法能夠得到沿井深連續分布的破裂壓力曲線,具有較高的縱向分辨率[2-4],且經濟可靠,因此被廣泛應用于鉆井工程。

關于地層破裂壓力預測模型和方法的研究很多。HUBBERT等[5]通過三軸壓縮試驗構建了首個地層破裂壓力預測模型,即Hubbert-Willis模型。MATTHEWS等[6]將骨架應力系數引入Hubbert-Willis模型,形成了新的地層破裂壓力計算模型。HAIMSON等[7]在水力壓裂裂縫起裂和延伸規律研究的基礎上,結合Biot有效應力原理推演了考慮滲流作用的破裂壓力預測模型。EATON[8]首次在破裂壓力計算模型中引入了泊松比參數,并將上覆巖層壓力設為變量,利用泊松比函數關系來表示上覆巖層壓力與地層孔隙壓力的關系。ANDERSON等[9]基于水平應力均勻條件,在地層破裂壓力計算模型中引入了Biot彈性多孔介質的應力和應變關系,構建了Anderson模型,該模型考慮了井壁應力集中造成的影響。STEPHEN[10]考慮了構造應力對破裂壓力的影響。黃榮樽[11]構建的破裂壓力預測模型考慮了巖石抗張強度的影響,即黃榮樽模型。譚廷棟[12]提出了地層破裂壓力上下限的概念。李傳亮等[13-14]根據多孔介質的雙重有效應力概念,提出了一種巖石破裂壓力計算公式,隨后研究了射孔完井條件下油井壓裂過程中巖石破裂壓力的計算公式。李培超[15]通過引入射孔深度參數改進了李傳亮[14]提出的射孔完井破裂壓力預測模型,構建了垂直井射孔完井破裂壓力計算模型。郭建春等[16]考慮了巖石礦物組成、酸類型、酸用量、溫度等對破裂壓力的影響,結合損傷力學、斷裂力學和有限元基本原理,建立了酸損傷射孔井儲集層破裂壓力的定量預測模型。趙金洲等[17]基于彈性力學和巖石力學理論,綜合考慮了裂縫與孔眼的空間關系以及水力壓裂裂縫的破裂模式,建立了裂縫型地層射孔井的破裂壓力計算模型。楊兆中等[18]考慮了套管、水泥環影響,結合最大拉應力、張性破壞和剪切破壞三種破裂準則,建立了煤層氣直井破裂壓力預測模型。不同的破裂壓力預測模型和方法具有不同的適用條件,可根據所研究工區的特點,選擇適用的預測模型和方法,得到較為可靠的破裂壓力預測結果。但是,無論是通過室內巖樣實驗還是基于測井資料估算,都只能獲取單個樣點或井筒處的地層破裂壓力數據,缺乏地層破裂壓力空間展布的信息。

本文針對頁巖地層各向異性的特點,提出了一種面向頁巖地層的破裂壓力地震預測方法。該方法在黃榮樽地層破裂壓力預測模型的基礎上,根據文獻[19]至文獻[21]的思想,引入了表征各向異性特征的各向異性應力耦合因子,構建了更為全面的頁巖各向異性破裂壓力預測模型,并基于該模型,通過方位疊前地震反演、巖石強度參數預測和地層壓力預測,開展頁巖地層的破裂壓力預測。

1 方法原理

1.1 頁巖各向異性破裂壓力預測模型

1984年,黃榮樽[11]提出了一種地層破裂壓力預測方法,并綜合考慮了巖層上覆應力、井壁應力集中、地下非均勻分布的構造應力及巖層強度等因素的影響,構建了一個地層破裂壓力預測模型:

(1)

式中:σ為泊松比,Pp為孔隙壓力,S為上覆巖層壓力,St為巖石的抗張強度,k=α-3β表示非均勻分布的地質構造應力系數,α和β表示水平兩個主方向的構造應力系數。

公式(1)中的應力耦合項σ/(1-σ)是各向同性的,而頁巖地層具有較強的各向異性特征,因此VERNIK等[19]、HU等[20]和THOMSEN[21]引入了各向異性應力耦合因子的概念,利用VTI介質中的彈性剛度常數C13和C33的比表示各向異性應力耦合因子,即將模型中的各向同性應力耦合因子σ/(1-σ)替換為各向異性應力耦合因子C13/C33,使其更符合實際頁巖地層的各向異性特征。借助這一思想,我們對公式(1)進行了改寫:

(2)

公式(2)模型中的k值根據實際工區鉆取的巖心樣品的地層破裂壓力實驗結果確定。一般來說,k值越大,對破裂壓力預測結果的影響越大,k值越小,影響就越小。因此在后續工作中可以繼續從已知井中獲取巖心樣品進行多次相同環境和條件下的地層破裂壓力實驗,對工區的構造應力系數不斷修正,使其逼近真實的數值。通常情況下,一個工區內部的構造應力系數可視為常值[11]。

1.2 基于方位地震數據的巖石力學參數地震預測方法

疊前地震反演是獲得儲層彈性參數(縱波速度、橫波速度、密度、楊氏模量、泊松比等)和裂縫巖石物理參數(法向弱度、切向弱度等)的重要手段[22-25]。利用方位地震數據中豐富的有效信息可以得到用于描述裂縫型儲層特征的關鍵參數,實現與巖石力學性質更相關的楊氏模量、泊松比、裂縫巖石物理參數的直接反演,避免了密度項反演不準確造成的換算累積誤差,提高彈性模量的反演精度,并為地層破裂壓力預測提供數據支撐。1996年,RUGER[26]推導了HTI介質的方位反射系數近似方程:

(3)

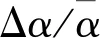
(1-2g)ΔN+(gcos2φsin2θ)ΔT

(4)

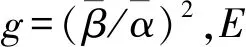
ε=2g(1-g)ΔN

(5)

δ=2g(ΔN-ΔT)

(6)

γ=ΔT/2

(7)

根據VTI介質彈性剛度常數與各向異性參數的關系:

(8)

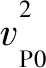
(9)

(10)

利用疊前地震反演得到的彈性參數和裂縫巖石物理參數,可以估算各向異性應力耦合因子C13/C33。其中,vP0和vS0分別為VTI介質的縱、橫波速度。當研究區域的地層為各向同性時,VTI介質彈性剛度常數中的各向異性參數為0,則各向異性應力耦合因子可以退化為各向同性應力耦合因子。

1.3 頁巖的巖石強度參數預測方法

巖石強度參數主要是指抗壓強度、抗張強度、內聚力與內摩擦角等參數。目前大部分巖石強度參數的預測主要基于巖心實驗測量或測井資料,本文基于巖石強度參數經驗公式獲得巖石強度參數數據體,為地層破裂壓力的預測提供數據支持。

巖石抗壓強度(Sc)是指巖樣被擠壓至整體破壞時,所能承受的最大應力值[31]。它與楊氏模量和泥質含量具有一定的統計關系,經驗公式如下[1]:

Sc=aE(1-Vsh)+bEVsh

(11)

式中,E為楊氏模量,Vsh為泥質含量,a和b為不同巖性的近似系數。GATENS等[32]和HEMINGWAY等[33]研究了泥頁巖地層a和b的估算值,分別為4.59和8.16。本文通過彈性參數疊前地震反演得到的楊氏模量E以及物性參數疊前反演得到的泥質含量Vsh[34-35]估算巖石抗壓強度Sc。

巖石的抗張強度(St)是指巖樣被拉伸至整體破壞時,所能承受的極限應力。它與楊氏模量E和泥質含量Vsh也有一定的統計關系,近似公式為[1]:

St=3.75×10-4E(1-0.78Vsh)

(12)

也可以用抗壓強度求取巖石的抗張強度,近似公式為:

St=Sc/m

(13)

式中,m為根據所研究區域的巖性特征而確定的系數,一般取值8～20。HEMINGWAY等[33]根據地區經驗和實例分析結果,認為泥頁巖地層中的m值一般取12左右。

1.4 基于波阻抗的地層壓力預測方法

地層壓力又稱孔隙流體壓力,是指作用于巖層孔隙空間內流體上的壓力[36]。RASOLOFOSAON等[37]提出了基于波阻抗的地層壓力預測方法,該方法基于有效應力原理,通過地層壓力與縱波阻抗良好的相關性實現地層壓力預測。目前基于地震資料獲取縱波阻抗的技術較為成熟,基于波阻抗預測的地層壓力具有較高的分辨率[36]。EATON[38]給出了地層壓力預測模型:

Pp=Pov-(Pov-Phy)(v/vnct)n

(14)

式中:Pov為上覆巖層壓力,Phy為靜水壓力,v為地震層速度,vnct為正常壓實條件下的地震層速度,n為Eaton常數,由實際數據擬合得到。將公式(14)進行改寫:

(15)

基于波阻抗的地層壓力預測方法如下:首先通過常規波阻抗反演得到高精度波阻抗數據Ip;其次利用單井資料計算得到的正常壓實速度vnct,結合地質層位信息,采用克里金插值方法構建正常壓實速度趨勢體;然后利用地層水密度數據體和反演得到的地層巖石密度數據體ρ,對密度沿深度進行積分,得到三維靜水壓力Phy與上覆巖層壓力Pov數據體;最后將波阻抗Ip、正常壓實速度趨勢體vnct、密度ρ、上覆巖層壓力Pov和靜水壓力Phy代入公式(15),得到地層壓力及壓力系數[36]。

1.5 頁巖地層的破裂壓力地震預測方法

基于上述方法技術,頁巖地層的破裂壓力地震預測方法如下:首先利用方位地震數據開展巖石力學參數地震預測,反演得到與巖石力學性質更相關的楊氏模量、泊松比、密度、法向弱度和切向弱度,進而估算各向異性應力耦合因子C13/C33;其次利用反演得到的彈性參數和物性參數,根據巖石抗壓強度與楊氏模量和泥質含量的統計關系得到抗壓強度,再通過巖石抗壓強度與抗張強度的關系估算抗張強度;然后根據地層壓力預測模型,采用基于波阻抗的地層壓力預測方法,得到上覆巖層壓力和孔隙壓力;最后基于頁巖各向異性破裂壓力預測模型,利用方位疊前地震反演、巖石強度參數預測、地層壓力預測方法得到的彈性參數、裂縫巖石物理參數、巖石強度參數、上覆巖層壓力和孔隙壓力參數,實現地層破裂壓力的地震預測。圖1 為該方法的技術流程。

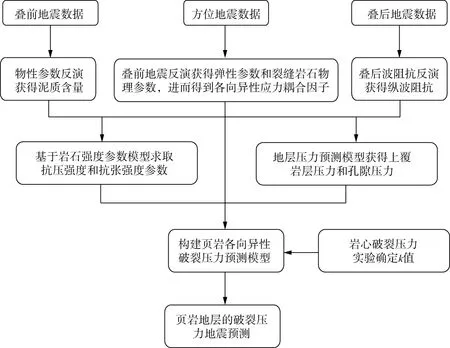
圖1 頁巖地層破裂壓力地震預測方法技術流程

2 實際資料應用

實際資料選自我國西部某頁巖工區,利用本文方法開展了該區頁巖地層的破裂壓力地震預測。圖2為反演得到的楊氏模量、泊松比、密度、法向弱度和切向弱度,可以看出反演結果與測井解釋結果吻合。在目的層處(圖中箭頭所指處)裂縫巖石物理參數為高值,表明該處具有較強的各向異性特征。圖3為采用頁巖巖石強度參數預測方法得到的抗壓強度與抗張強度(本文實際應用時選擇公式(13)獲取抗張強度)。可以看出預測結果與測井解釋結果較為吻合,在目的層井所在位置處,抗壓強度與抗張強度為低值。圖4為地層壓力預測方法得到的上覆巖層壓力和孔隙壓力,在目的層處孔隙壓力為高值,上覆巖層壓力隨著深度的增加而逐漸升高。圖5 為地層破裂壓力預測結果。從圖5可以看出,利用地震數據估算的地層破裂壓力預測結果與測井解釋結果較為吻合,驗證了本文方法的可行性和可靠性。該成果可為頁巖地層水平井設計和優化方案及壓裂改造等工程施工提供可靠的參考數據。

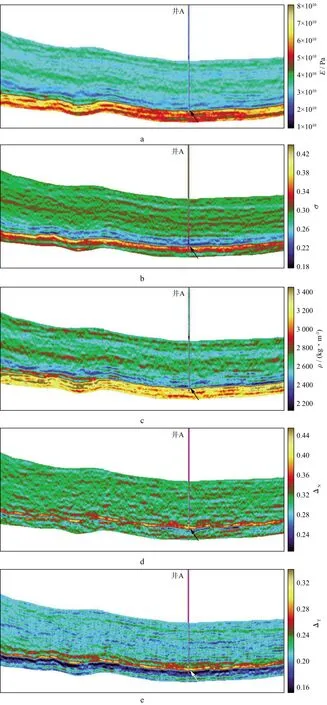
圖2 彈性參數和裂縫巖石物理參數反演結果a 楊氏模量; b 泊松比; c 密度; d 法向弱度; e 切向弱度

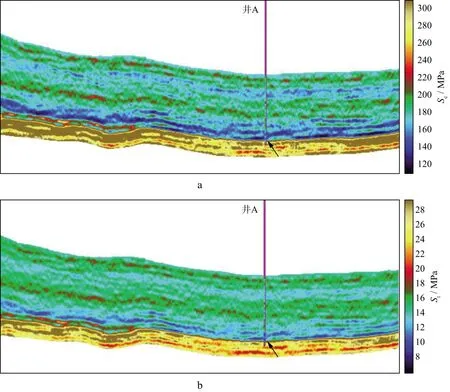
圖3 巖石強度參數預測結果a 抗壓強度; b 抗張強度

圖4 地層壓力預測結果a 孔隙壓力; b 上覆巖層壓力

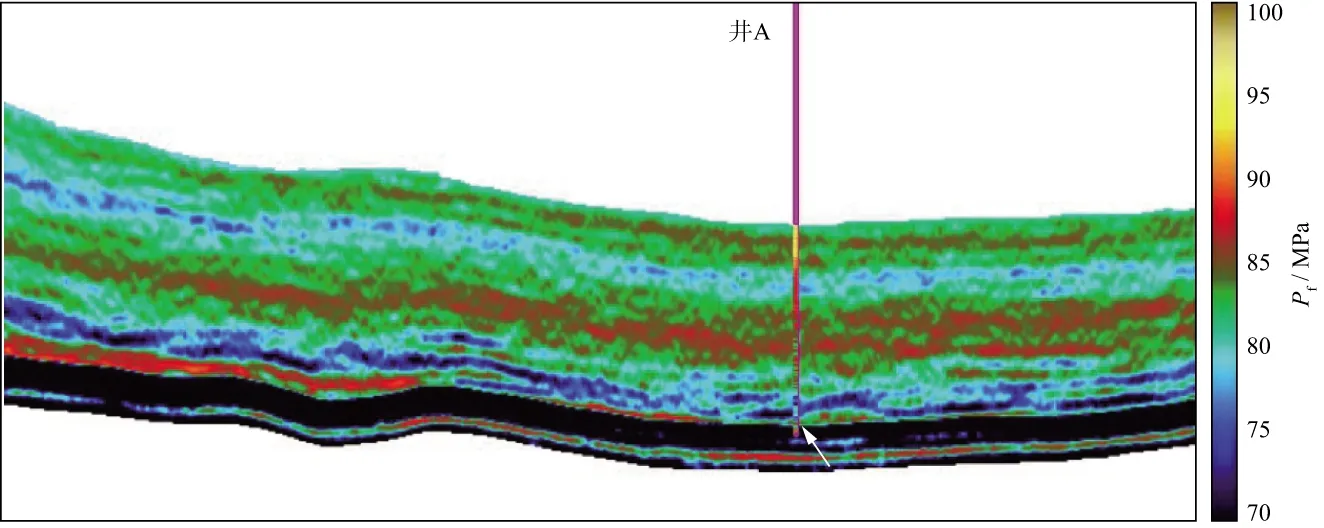
圖5 地層破裂壓力預測結果

3 結束語

本文針對頁巖地層具有強各向異性的特點,基于改進的頁巖各向異性破裂壓力預測模型,研究了頁巖地層的破裂壓力地震預測方法,并將該方法應用于我國西部某頁巖工區,得出以下結論:

1) 基于改進的各向異性破裂壓力預測模型,利用頁巖地層的破裂壓力地震預測方法得到的破裂壓力預測結果更符合實際頁巖地層特征。

2) 根據構建的頁巖各向異性破裂壓力預測模型,利用地震數據及疊前地震反演方法、巖石強度參數預測方法、地層壓力預測方法,能夠得到整個工區的地層破裂壓力空間展布,為靶區的鉆井設計和壓裂施工等提供可靠的參考依據。

3) 巖石力學參數對于壓裂效果的評價至關重要,因此前期的疊前地震反演方法、巖石強度參數預測方法和地層壓力預測方法應不斷完善,盡可能提高各個參數反演和預測的可靠性和精度,為后續的地層破裂壓力預測提供可靠的基礎數據。