基于聚類與SVR的地區支線航空客運市場需求預測

徐夢瑤 趙鳴 李洋 安洋 張友浩

摘 要：針對支線航空客運市場需求預測問題，某些地區（如海南）缺少足夠的歷史數據，難以建立準確的預測模型。本文提出基于聚類與支持向量機回歸（Support Vector Regression，SVR）預測此類地區航空客運市場需求的方法。首先，基于中國各個地區支線航空客運市場需求的分布比，找出與海南分布比相似的地區，再應用系統聚類法在這些地區中找出與海南聚為一類的地區，作為類比地區。然后，選擇類比地區的數據樣本，通過K-fold 交叉驗證（K-fold Cross Validation，K-CV）尋優SVR 參數，得到預測模型。最后，預測了2018～2020年海南支線航空客運市場需求，從而為其建設支線機場提供一定的決策參考和可靠的理論依據，具有一定的現實意義和應用價值。

關鍵詞： 支線航空;客運市場需求;預測;系統聚類;SVR

【Abstract】 For predicting the market demand of regional air transportation for passengers， some regions （such as Hainan） lack enough available data to establish accurate prediction models. This paper proposes a method based on Clustering and Support Vector Regression （SVR） to predict the market demand of air transportation for passengers in such regions. Firstly， the paper finds the similar regions to Hainan in distribution ratio of the market demand， then compares Hainan with these regions which were clustered together. Secondly， the paper selects the data samples of the similar regions and forms a prediction model after getting the SVR parameters by K-fold Cross Validation （K-CV）. Finally， the paper predicts the market demand of Hainan air transportation for passengers from 2018 to 2020. The results could provide theoretical support and guidance for constructing new regional airports， which is realistic and practical value to some extent.

【Key words】 ?regional aviation; passenger market demand; prediction; hierarchical cluster; SVR

0 引 言

中國民航局的相關資料顯示，從2011～2016 年，國內支線航線網絡增加了27%，運力增加了116%。預計到2020 年，支線航空客運量將會突破1 億人次，其發展速度約為干線航空的兩倍[1]。國內支線機場在綜合交通運輸體系中發揮著越來越大的作用，因而為了抓住擴建支

線機場數量的最佳有利時機，并減少支線機場建設的盲目性，即需對地區支線航空客運市場需求做出預測，提高針對性，同時也將對地區的支線機場建設和實際生產有著積極的指導意義。但是對于某些地區，如果支線機場通航時間較短，幾乎無可用的歷史數據，就使得支線航

空客運市場需求的預測研究受到了一定的阻礙。

眾多學者已經對這種缺少歷史數據支撐的客貨運需求預測問題展開了大量研究。張娜等人[2]提出了先通過快速聚類找出與新建機場相似的機場，再利用相似機場的航空分擔率來預測新建機場客運量的方法。悅慧等人[3]運用動態聚類法找出與新建機場屬于同類的機場，基于同類機場的歷史數據構建多元回歸模型，從而預測新建機場的客運量。但由于航空客運需求預測所受噪聲和影響因素較多，并且各因素對支線航空客運市場需求的影響程度也不盡相同，這使得支線航空客運市場需求預測具有高度非線性的特點。故簡單的多元線性回歸模型已經不能滿足預測需求。羅建鋒等人[4]將機器學習的方法運用在新建機場貨郵量預測上，即先利用相近周邊機場航空貨運量占社會總貨運量的比例關系，并結合本地區GDP與航空貨運量、旅客吞吐量與航空貨郵量的比例關系進行校核，從而擬合出新建機場航空貨郵量的歷史數據，再將歷史數據帶入BP神經網絡，預測新建機場的貨郵量。BP神經網絡方法雖然能很好地處理非線性問題，但對于航空客運量預測這種影響因素較多且樣本量較小的預測問題仍具有較大局限性，其預測出的精度較低[5]。

支持向量機（Support Vector Machine，SVM）是VAPNIK提出的一種建立在統計學理論的VC維理論和結構風險最小化原理基礎上的機器學習方法[6]。支持向量機回歸（Support Vector Regression， SVR）是由SVM 衍生得到的，在解決小樣本、非線性、高維度問題中顯示出了絕對的優勢[7-8]。在SVR的應用過程中，懲罰參數C與核函數參數g的選取對預測結果的影響很大，如何選取合適的參數成為問題的關鍵。趙靜等人[9]采用了K-fold交叉驗證（K-fold Cross Validation，K-CV）模型選擇最優參數，提高了預測的精度。在前述研究的基礎上，本文提出基于聚類與SVR預測支線航空客運市場需求的研究設計。

1 支持向量機回歸（SVR）的基本原理

2 海南支線航空客運市場需求分析

2.1 研究方法與思路

本文對支線機場的界定需要滿足2 個條件，對此可闡述為：

（1）年旅客吞吐量占全國旅客總吞吐量的比例小于0.2%。

（2） 機場處于非國家中心城市、非省會城市，屬于非樞紐性機場[11]。

海南地區的支線機場現有瓊海博鰲機場和三沙永興機場，2 個支線機場都是2016 年通航，通航時間短，且缺乏歷史數據。對數據樣本缺乏或較少的通航地區，如海南的支線航空客運市場需求預測就轉化為對旅客吞吐量的預測，以整體把握該地區支線航空客運市場未來的發展趨勢。

本文研究思路是：首先，基于全國和各地區支線機場旅客吞吐量，提出各個地區支線航空客運市場需求的分布比。接著找出與海南分布比相似的地區，再應用系統聚類法在這些地區中求出與海南聚為一類的地區，作為類比地區。然后，將選定地區的歷史值作為訓練數據，代入SVR 預測模型，通過K-CV 尋優SVR 參數，確定預測模型。最后，對海南的支線航空旅客吞吐量進行預測，為其建設支線機場提供一定的決策參考。本文的技術研發路線如圖1所示。

2.2 類比地區的選擇

2.2.1 地區支線航空客運市場需求分布比

中國幅員遼闊、地形地貌差異較大，不同的地域條件導致了中國支線機場分布的不均衡，也影響著機場旅客吞吐量。本文引入分布比的概念[12]，定義了某地區支線航空客運市場需求分布，即某地區支線機場旅客吞吐量與全國支線機場旅客吞吐量的比值。研究推得其數學公式可寫為：

γ=T地區T全國×100%.（6）

其中，γ 表示某地區支線航空客運市場需求分布比; T地區表示某地區支線機場旅客吞吐量，單位為：人; T全國表示全國支線機場旅客吞吐量，單位為：人。

中國各個地區支線航空客運市場需求分布比如圖2 所示。海南位于國內中南地區，由圖2可知，中南地區與西南地區的支線航空客運需求基本處于相同水平，都在10%～23%之間。故從這2 個地區中選取貴州、四川、西藏、云南、重慶、廣東、廣西、海南、河南、湖北、湖南11 個省份作為類比樣本。

2.2.2 分布比相似地區的系統聚類

從影響支線航空客運需求的人口、地區經濟發展情況的角度來考慮，選擇人口密度、人均GDP、城鎮居民人均可支配收入、城鎮居民人均消費支出4 個指標作為聚類的評價指標。選取2008～2017 年各地區指標值的平均值作為樣本數據。用系統聚類法對樣本數據進行聚類。由此得到的分布比相似地區的聚類樹圖即如圖3 所示。

由圖3可知，海南、廣西、四川聚為一類。由于廣西與海南同屬于中南地區，且廣西與海南地理位置靠近，與海南的人口密度、人均GDP、城鎮居民人均可支配收入、城鎮居民人均消費支出也非常相近。故最終選擇廣西作為海南的類比地區。

3 基于SVR的模型構建與預測

3.1 模型構建

因海南與廣西同屬一類，且廣西數據充足，將廣西的人口密度、人均GDP、城鎮居民人均可支配收入、城鎮居民人均消費支出4組數據作為輸入特征值，年旅客吞吐總量作為輸出特征值。選擇廣西2008～2016年的9組數據作為SVR模型的訓練樣本，2017年數據作為測試樣本。研發設計步驟可剖析分述如下。

（1）用Matlab中的mapminmax函數來對10組樣本數據進行歸一化處理，防止特征值范圍過大或過小，影響模型的精確度。其中，歸一化的范圍為[-1，1]。

（2）選擇SVM的類型為ε-SVR，核函數選取精度較高的RBF函數[13-14]。設置ε-SVR中的損失函數p的值為0.1。

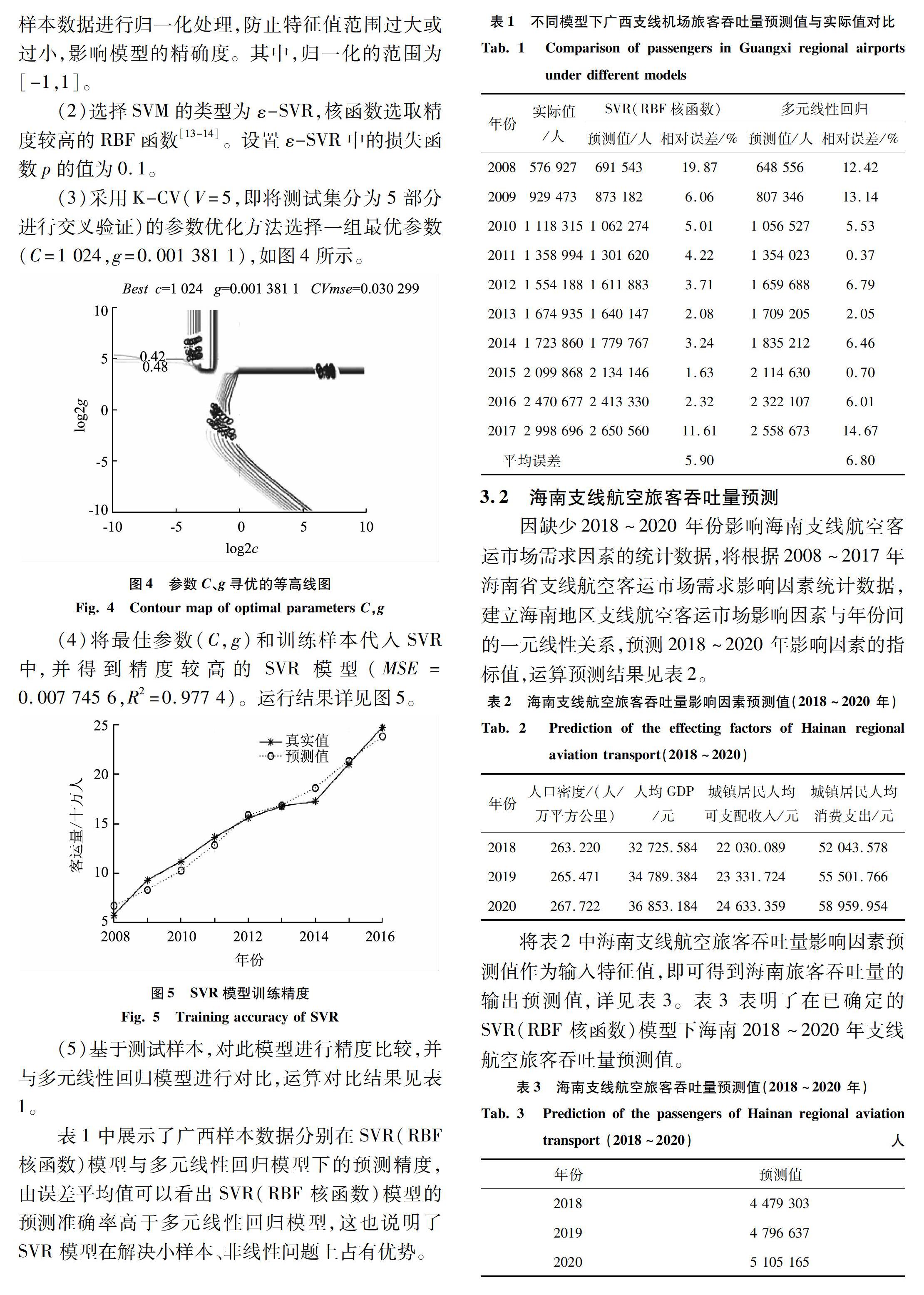
（3）采用K-CV（V=5，即將測試集分為5部分進行交叉驗證）的參數優化方法選擇一組最優參數（C=1 024，g=0.001 381 1），如圖4所示。

（4）將最佳參數（C，g）和訓練樣本代入SVR中，并得到精度較高的SVR模型（MSE=0.007 745 6，R2=0.977 4）。運行結果詳見圖5。

（5）基于測試樣本，對此模型進行精度比較，并與多元線性回歸模型進行對比，運算對比結果見表1。

表1中展示了廣西樣本數據分別在SVR（RBF 核函數）模型與多元線性回歸模型下的預測精度，由誤差平均值可以看出SVR（RBF 核函數）模型的預測準確率高于多元線性回歸模型，這也說明了SVR 模型在解決小樣本、非線性問題上占有優勢。

3.2 海南支線航空旅客吞吐量預測

因缺少2018～2020 年份影響海南支線航空客運市場需求因素的統計數據，將根據2008～2017年海南省支線航空客運市場需求影響因素統計數據，建立海南地區支線航空客運市場影響因素與年份間的一元線性關系，預測2018～2020 年影響因素的指標值，運算預測結果見表2。

將表2 中海南支線航空旅客吞吐量影響因素預測值作為輸入特征值，即可得到海南旅客吞吐量的輸出預測值，詳見表3。表3 表明了在已確定的SVR（RBF 核函數）模型下海南2018～2020年支線航空旅客吞吐量預測值。

4 結束語

針對某些地區（如海南）缺少足夠的歷史數據，難以建立航空客運市場需求預測模型的問題，本文提出基于聚類與SVR預測支線航空客運市場需求的方法。根據類比法的思想，首先，選取與海南地區機場旅客吞吐量分布比相似的地區（如貴州、四川、西藏等）進行系統聚類，找出類比地區（廣西）。然后，選擇廣西省2008～2017年的數據樣本，通過K-CV尋優SVR參數（C=1 024，g=0.001 381 1），得到預測模型。將此模型與多元線性回歸預測方法進行精度比較，證明SVR （RBF核函數）預測模型具有更好的預測效果。基于此模型，預測了2018～2020年海南支線航空旅客吞吐量，從而為其建設支線機場提供一定的決策參考和可靠的理論依據，具有一定的現實意義和應用價值。

參考文獻

[1]張一琛.支線航企如何"叫好又叫座"[J].大飛機，2017（3）：28-31.

[2]張娜，安然.基于快速聚類分析的航空分擔率模型在新建機場客運量預測中的應用[J].交通與計算機，2008，26（4）：116-119.

[3]悅慧，安然.多元回歸模型在新建機場客運量預測中的應用研究-基于動態聚類分析[J].現代商貿工業，2010，22（20）：13-15.

[4]羅建鋒，周凌云，李偉.基于BP神經網絡的新建支線機場貨郵量綜合預測[J].江蘇商論，2012（2）：47-49.

[5]曾鳴，林磊，程文明.基于LIBSVM和時間序列的區域貨運量預測研究[J].計算機工程與應用，2013，49（21）：6-10.

[6]VAPNIK V N. The nature of statistical learning theory[M]. New York： Springer， 2000.

[7]ABDI M J， GIVEKI D. Automatic detection of erythemato-squamous diseases using PSO-SVM based on association rules[J]. Engineering Applications of Artificial Intelligence， 2013 ， 26（1）：603-608.

[8]LIU Zhiwen， CAO Hongrui， CHEN Xuefeng， et al. Multi-fault classification based on wavelet SVM with PSO algorithm to analyze vibration signals from rolling element bearings[J]. Neurocomputing， 2013，99：399-410.

[9]趙靜，王選倉，丁龍亭，等.基于灰色關聯度分析和支持向量機回歸的瀝青路面使用性能預測[J].重慶大學學報，2019，42（4）：72-81.

[10]張文雅，范雨強，韓華，等.基于交叉驗證網格尋優支持向量機的產品銷售預測[J].計算機系統應用，2019，28（5）：1-9.

[11]李飛行，宋一鑫，張權.我國支線機場現狀分析及對策研究[J].交通運輸研究，2018，4（4）：61-68.

[12]周明妮. 新建支線機場通航可行性論證方法研究[D]. 西安：長安大學，2011.

[13]AYDIN I， KARAKOSE M， AKIN E. A multi-objective artificial immune algorithm for parameter optimization in support vector machine[J]. Applied Soft Computing， 2011， 11（1）：120-129.

[14]de CASTRO L N， von ZUBEN F J. Learning and optimization using the clonal selection principle[J]. IEEE Transactions on Evolutionary Computation， 2002，6（3）： 239-251.