傅里葉變換紅外光譜儀量化誤差仿真分析

袁錢圖 邵麗萍 白忠臣

摘 要：分析了數模轉換器的量化誤差對傅里葉變換紅外光譜精度的影響。采用積分轉離散求和的方法對干涉圖進行建模仿真分析。將干涉圖信號經過8位、12位、16位以及20位數模轉換器轉換之后進行快速傅里葉變換，最后解譜光譜數據。同時，也定量比較了不同位數的數模轉換器的光譜圖相較于原始光譜圖的偏離程度，以及在吸收峰位置分析量化誤差對光譜圖偏移的影響。結果表明，20位數模轉換器的平均偏離誤差為1.884 97，且該模型可作為由量化誤差引起相關誤差的修正算法的理論依據。

關鍵詞： 傅里葉變換光譜儀;紅外吸收光譜;量化誤差;邁克爾遜干涉儀

【Abstract】 The influence of quantization error on infrared spectral accuracy of Fourier transform is analyzed. The method of integral to discrete summation is used to model and simulate the interferogram. The interferogram signal is subjected to fast Fourier transform after converted by digital-to-analog converters with 8 bit， 12 bit， 16 bit， and 20 bit， and the spectrum data is decoded. At the same time， the deviation degree between the spectrum diagram of the digital-to-analog converter with different bits and the original spectrum is quantitatively compared ， and the influence of quantitative error for the spectrum migration is analyzed at the position of the absorption peak. The result shows that the average deviation error of the 20 bit digital-to-analog converter is 1.884 97， and the model can be used as the theoretical basis on the correction algorithm of correlation error caused by quantization error.

【Key words】 ?Fourier transform spectrometer; infrared absorption spectrum; quantization error; Michelson interferometer

0 引 言

傅里葉變換紅外光譜（Fourier transform infrared spectroscopy， FTIR）自從19世紀中后期發明問世以來，迄今已經得到了廣泛的應用[1]。特別適用于近紅外和中紅外光譜測量分析生物和化學材料的成分，具有高分辨率和高信噪比等優點，只需要一個光電探測器就可以完成干涉圖的獲取，既節約了成本，也減小了設備體積[2]。傅里葉變換紅外光譜，利用的是干涉圖和光譜圖互為傅里葉積分對的關系，通過對干涉信號進行傅里葉積分變換的方法來測定和研究光譜[3-4]。20世紀中葉，兩大優點高光通量和多通道的發現助推了傅里葉變換紅外光譜學的快速發展[5]。而另一項對于傅里葉變換紅外光譜學的發展起決定性作用的就是快速傅里葉變換算法的成功研發[6]。相較于常規的傅里葉變換運算，Cooley-Tukey提出的快速傅里葉變換算法在運算速度上提高了幾個數量級，為傅里葉變換紅外光譜測量技術的廣泛運用奠定了基礎。

通常的傅里葉變換紅外光譜儀工作原理如圖1所示。入射光經邁克爾遜干涉儀產生干涉，使得在光電傳感器處可以探測到干涉信號。放大器將微弱的干涉信號進行I/V轉換、電壓放大和濾波，數模轉換器將干涉模擬信號轉換數字信號。最后利用傅里葉積分變化將干涉信號進行解譜得到被測物的吸收光譜。

雖然傅里葉變換紅外光譜技術目前已然漸趨成熟，但在實際使用中不可避免地會產生誤差。準確分析傅里葉變換紅外光譜儀的測量誤差對于減少噪音，提高精度顯得尤為重要。研究可知，數模轉換器在將光電探測器檢測到的模擬信號進行數模轉換時將會帶來量化誤差，誤差過大就會導致輸出信號的不平滑[7]。李妍[8]和熊偉[9]均對量化誤差做出過研究，但并未對量化誤差所導致的光譜偏離進行分析。因此本文的研究致力于通過仿真分析的方法定量分析量化誤差對光譜的影響。

1 量化誤差

數模轉換器指的是將模擬量轉換為數字量的電子元器件。數字信號的大小是一個相對的值，與數模轉換器的參考模擬量的大小相關。模數轉換器的性能，可以用轉換精度來衡量。轉換精度慣用其輸出的數字信號的最大位數來表示。性能越好、精度越高的數模轉換器，輸出的數字量的位數也就越高，輸出信號的失真也就越少。

量化是指將輸入模擬量信號的幅值進行離散化處理，即將輸入模擬信號用一個最接近數模轉換器可識別的最小數量單位的整數倍來代換[10]。例如將10 V的信號分成5份，那么可探測到的信號為0 V、1 V、2 V、3 V、4 V以及5 V，如果將信號分成10份，那么可探測到的信號為0 V、1 V、2 V、3 V、4 V、5 V、6 V、7 V、8 V、9 V以及10 V。分辨率越高，可探測到的信號也就越多，被淹沒的信息也就越少。

3.1 光譜圖建模分析

通過等光程差采樣得到的原始干涉圖如圖2所示，將圖形的部分進行放大，包含零光程差位置，可以看到流暢的曲線。干涉圖在零光程位置時干涉的強度達到最大值，雖然幅值在不斷地波動，但總體幅值從零光程差位置向兩端延伸時呈現遞減的趨勢，并且干涉圖關于零光程差位置對稱。

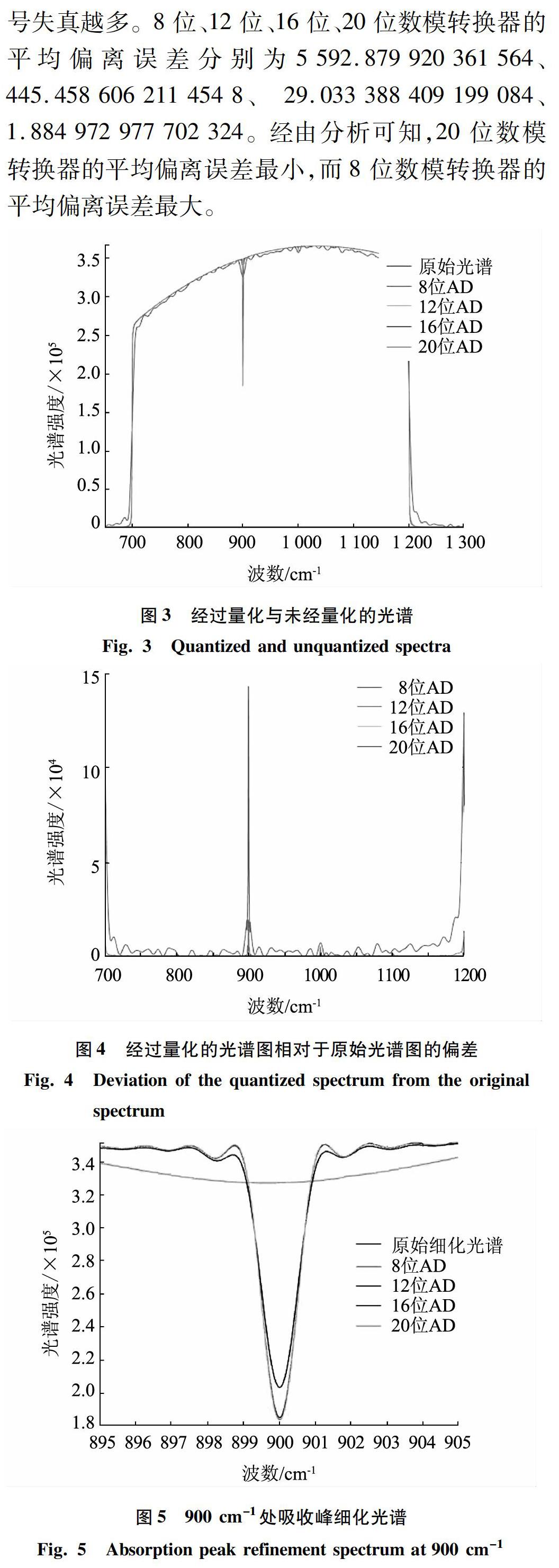
將原始干涉圖數據進行不同位數的數模轉換，得到的光譜圖如圖3所示。從光譜圖中可以看出數模轉換器的位數越小，光譜圖的波動越大。其數值就相對于原始光譜圖的數值偏離越大，所得到的光譜圖也就越不精確。

3.2 光譜圖偏差分析

為了量化光譜圖的偏離程度，將具有量化誤差的光譜圖數值減去對應位置的原始光譜圖的數值的絕對值來表示偏離程度，如圖4所示。數值越大，表示具有量化誤差的光譜圖偏離原始光譜圖越大，信號失真越多。8位、12位、16位、20位數模轉換器的平均偏離誤差分別為5 592.879 920 361 564、445.458 606 211 454 8、29.033 388 409 199 084、1.884 972 977 702 324。經由分析可知，20位數模轉換器的平均偏離誤差最小，而8位數模轉換器的平均偏離誤差最大。

由圖5可得到，900 cm-1處吸收峰的位置分別為（899.661，327 123.972 063 478 4）、（900.014，203 431.678 543 270 6）、（900.013，185 121.082 034 579 6）、（900.013，183 984.889 481 238 0）、（900.013，183 908.643 867 329 3）。經由分析可知，8位數模轉換器的吸收峰在縱坐標和橫坐標上偏離原始光譜的位置最大，而20位數模轉換器的吸收峰的位置誤差偏離最小。

根據實驗的數據可知，在4種數模轉換器中，20位的數模轉換器的量化誤差對光譜圖的精度影響最小，所得到的光譜圖最接近原始的光譜圖。而8位的數模轉換器的量化誤差對光譜的精度影響最大，所得到的光譜圖與原始光譜圖偏離最大。

4 結束語

本文通過積分轉離散求和的方式對干涉圖進行建模和計算得到干涉圖。定量分析了數模轉換器的量化誤差導致的光譜圖偏離。采用光譜細化技術分析了吸收峰的位置偏離。

通過仿真數據可知，數模轉換器的量化誤差會導致光譜幅值的偏離，并且量化誤差越大，偏離的也就越大。量化誤差會導致吸收峰峰位的改變。量化誤差越大，峰值就越偏離真實值。量化誤差會導致吸收峰橫坐標的向左或向右偏移。

在光譜的實際運用中可以通過此模型定量化分析傅里葉光譜的量化誤差，依據實際需求的光譜精度合理選擇適宜的數模轉換器，為高精度的傅里葉光譜儀提供理論依據。通過本文的建模仿真數據可知，數模轉換器的轉換精度越高，即量化誤差越小，解譜得到的光譜精度越高。

參考文獻

[1]相里斌. 傅里葉變換光譜儀中的主要技術環節[J]. 光子學報， 1997， 26（6）：550-554.

[2]SEREN H R ， HOLMSTROM S ， AYERDEN N P ， et al. Lamellar-Grating-Based MEMS Fourier transform spectrometer[J]. Journal of Microelectromechanical Systems， 2012， 21（2）：331-339.

[3]葉伏秋.基于FFT的傅里葉光譜Matlab仿真分析[J].吉首大學學報（自然科學版），2011，32（1）：49-51，62.

[4]沈學礎.傅里葉變換光譜學—引論和進展[J].物理學進展，1982，2（3）：275-322.

[5]林中，范世福. 光譜儀器學[M].北京：機械工業出版社，1989.

[6]陳晉.快速傅里葉變換的研究[J].黑龍江科學，2018，9（24）：62-63.

[7]李啟丙.高分辨率AD轉換器的研究[J].儀表技術與傳感器，2011（10）：93-95.

[8]李妍. 高性能FTIR光譜儀數據采集與處理方法研究[D].合肥：中國科學技術大學，2017.

[9]熊偉. 傅立葉變換紅外光譜儀測量誤差分析[D].武漢：華中科技大學，2009.

[10]ALBER G M ， MARSHALL A G . Effect of sampling rate on Fourier Transform spectra： Oversampling is overrated[J]. Applied Spectroscopy， 1990， 44（7）：1111-1116.

[11]趙新民，張寅.離散傅里葉變換量化效應的研究[J].計量學報，1992，13（3）：214-220.

[12]CLAASEN T A C M， JONGEPIER A. Model for the power spectral density of quantization noise[J]. IEEE Transactions on Acoustics Speech & Signal Processing， 1981， 29（4）：914-917.

[13]BENNETT W R. Methods of solving noise problems[J]. Proceedings of the IRE， 1956， 44（5）：609-638.

[14]陳尚松，郭慶，雷加.電子測量與儀器[M].2版.北京：電子工業出版社， 2009.

[15]李莉，牟同升.光纖光譜儀的波長校正[J].光學儀器，2008，30（3）：51-54.

[16]趙興， 聶昌， 呂艷玲. FTIR采樣誤差分析[J]. 硅谷， 2013（6）：76-78.

[17]張磊. 紅外傅立葉光譜儀信息處理技術研究[D]. 北京：中國科學院大學（中國科學院上海技術物理研究所），2017.

[18]褚建平. 基于CCD的小型化光譜儀的設計與研究[D].青島：中國海洋大學，2007.

[19]張磊，鄒曜璞，韓昌佩.紅外傅里葉光譜儀光譜細化的高速并行實現[J].紅外技術，2017，39（9）：848-854.