基于貝葉斯網絡的蟹塘養殖水質分析與預測?

夏潤清

（江蘇大學電氣與信息工程學院 鎮江 212013）

1 引言

河蟹養殖已成為水產養殖中最具活力和發展前景的支柱產業之一，其養殖方式以蟹塘養殖為主，而如何分析評估蟹塘水質對河蟹生長的適宜指數，并實時調控水質，已成為養殖的關鍵因素。國內對水質分析評估的方法較多，文獻［1］將模糊數學法應用于水質分析，有效地評估水質局部變化，但沒有給出水質變化趨勢以及水質因子間因果關系。文獻［2］將灰色聚類方法應用于水質分析，較準確地預測水質整體變化，也沒有給出水質因子間的因果關系。文獻［3］采用BP 神經網絡［4］進行水質預測分析，但水質環境變化具有不確定性，且是區域評估。

本文在收集陽澄湖河蟹養殖與配載中心近兩年蟹塘水質監測數據的基礎上，結合數據融合［5］技術，構建了反映水質因子與適宜指數之間關系的貝葉斯網絡模型［6］，利用貝葉斯網絡克服水質因子變化的不確定性，降低推理過程的復雜性，以期提高蟹塘水質評估的準確性，為健康的蟹塘養殖提供科學參考。

2 貝葉斯網絡構建

在陽澄湖各蟹塘設置多個水質傳感器［7］，構成監測節點組，所有水質數據通過4G網絡，傳送至養殖中心。由于同一塊蟹塘分布的各監測節點易受水位、光照等環境因素影響，需要對各水質數據進行數據融合，進而提高數據精度。水質數據的采集基于蟹塘養殖水質監測系統，系統構成如圖1 所示。

圖1 陽澄湖水質遠程監測系統架構框圖

2.1 傳感器數據融合

設Pi，j，i=1，2，…，b，j=1，2，…，s 為第i 類傳感器的第j 位置觀測值，且各傳感器的量測方差為σ2i，j，則水質參數的自適應加權數據融合為

2.2 水質指標選取

隨著水產養殖行業的發展，養殖手段益發科學、健康，相關養殖水質指標紛繁多樣，常見的水質指標如表1 所示。某些水質指標之間存在互相關性［8］，直接用于貝葉斯網絡，會導致模型結構過于復雜，且模型的預測精度也難以保證。為了減少水質指標之間的相關性，引入相關系數矩陣，對多個水質指標進行篩選，以期獲取相關性較小、代表性較強的水質指標。

以2016 年陽澄湖大閘蟹養殖與配載中心1 號蟹塘水質監測數據為樣本數據（如圖2 所示）。某些參數的變化趨勢相似，存在明顯的相關。為此，建立其相關系數矩陣的color map［9］（如圖3 所示），兩個水質指標之間的相關性越高，色彩越深，水質指標的篩選主要針對color map 中色彩較深的部分。

由圖3 可知，A3、A6、A10 與眾多水質因子有較高相關性，綜合專家經驗，舍去A3（EC）、A6（Chl-a）與A10（NO2N）兩個水質因子，用剩余水質因子構建貝葉斯網絡模型。

表1 水質指標及離散化標準

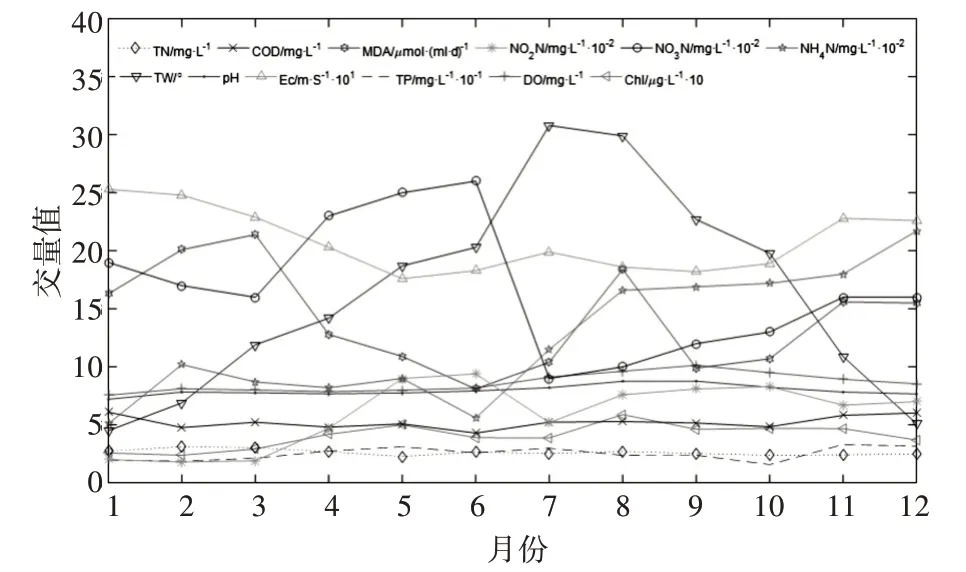
圖2 2016年一號蟹塘水質監測信息

圖3 水質因子相關系數矩陣的color map

2.3 貝葉斯網絡模型構建

貝葉斯網絡N 可以表示為二元組N=(G，Θ)，其中G=(V，E) ，V 是貝葉斯網絡的變量集，，且，即Xi取有限離散值，E 是變量對應的結點之間有向邊的集合，若存在有向邊由Xi指向Xj，則Xi被稱為Xj的父結點，反之，Xj為Xi的子結點，Xj的父結點集用pa(Xj)表示，Xi的子結點集用de(Xi)表示，而Θ={θ1，θ2，…，θn}表 示 結 點 Xj在 其 父 結 點 集pa(Xj)不同狀態下的條件概率表，是基于貝葉斯網絡做預測分析時的主要依據。

根據陽澄湖大閘蟹養殖與配載中心2010 年～2017 年各蟹塘的出蟹率，選取9 塊蟹塘，劃分成適宜河蟹養殖水質（A類）和一般河蟹養殖水質（B類）兩類，A類下轄8塊蟹塘，B類有1塊蟹塘，養殖時期的蟹塘水質指標數據1000組，總計9000組數據，對所選數據基于式（1）作數據融合處理，根據表1 水質指標零散化標準，再進行水質數據零散化處理，二次處理后的數據構成貝葉斯網絡模型的訓練數據集D。

貝葉斯網絡模型的結構學習采用著名的K2算法［10～11］，K2 算法依據評分函數獲取最優模型結構［12～13］。K2的打分公式：

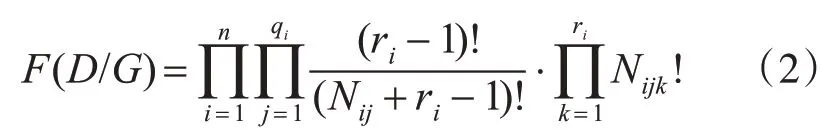
其中，G 是貝葉斯網絡結構，D 是訓練數據集，n 是水質指標與水質類別一起構成的結點數量，n=10，qi是pa(Xi)的配置數，配置數qi控制K2打分公式計算的順序與復雜程度，qi≤9000，ri表示結點Xi的可能取值數量，Nijk表示訓練數據集D中滿足條件：配置數qi=j，Xi=Xki 的實例數，并且有

鑒于水質指標數量較多，貝葉斯網絡結構學習復雜，本文K2 打分公式可以分解到與每個結點對應的局部測度，簡化結構學習過程。K2 的局部打分公式為

K2 算法需要水質變量之間存在既定的變量序，譬如變量序中結點Xi排在Xj之前，則Xj不會作為Xi的父節點。依據蟹塘養殖專家知識，對九個水質變量以及蟹塘水質類別這十個結點預先排序，X10為最前序列。同時，限定各結點最大父節點數

K2 算法打分公式的應用較為復雜，以如下例子做詳細說明：pH，TN，TW 是蟹塘養殖中的三個水質結點變量，三者構成簡單的貝葉斯網絡，假設根據已有知識可以確定貝葉斯網絡可能為圖4 中A、B兩種結構，數據集D0見表2。

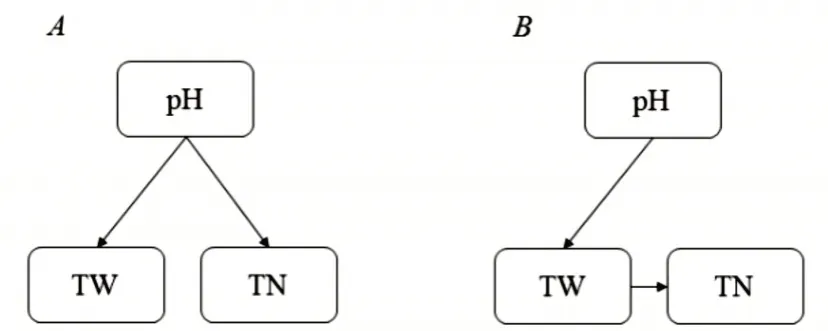
圖4 實例貝葉斯網絡結構

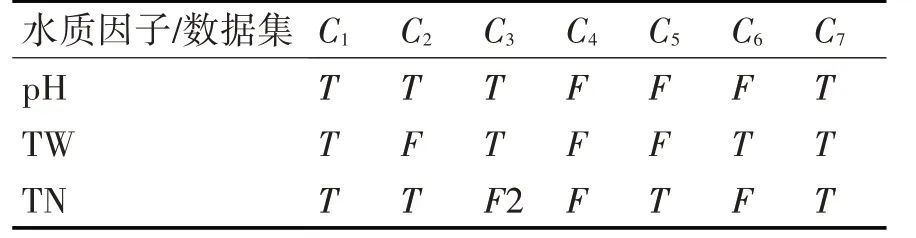
表2 訓練數據集D0

貝葉斯網絡在K2算法下的結構學習以打分公式為結構篩選依據，步驟如下：

K2算法偽代碼：

k2(X，O，m，D，πi)

輸入： X={X1，X2，…，Xn} %變量結點O%結點順序

m%變量父節點個數的上界

D%完整數據集

πi%結點Xi的父節點集

輸出：貝葉斯網絡

步驟實現：

for i=1 to n do

πi=?;

Z=?;

Fold=f(i，πi;%k2打分 )

Start=true;

while Strat( t rue) and |πi|＜m do

Z ←結點集Xexcept( Xi)-πi中使

f( i ，πi∪{Z })達到最大的結點；

Fnew=f( i ，πi∪{Z });

if Fnew＞Foldth en Fold=Fnew;

πi=πi∪{ Z };

else Start=false;

end if

end while

return(πi) ;

end for

通過K2 算法對訓練數據集D 的學習，借助Netica［14～15］編譯，獲得了反映蟹塘水質與水質指標之間關系的貝葉斯網絡，如圖5所示。

圖5 陽澄湖蟹塘水質貝葉斯網絡

易見，Tw、TN、TP、NO3-_N、NH4+_N、MDA 是直接決定蟹塘水質是否適宜河蟹生長的水質指標，屬于主導因素，pH、COD、DO 屬于輔助因素，在分析預測時可以賦予較小的權重。因此，依據獲得的貝葉斯網絡模型作水質預測分析時，圍繞Tw、TN、TP、NO3-_N、NH4+_N、MDA這六個變量進行。

2.4 模型推理

基于貝葉斯網絡模型的因果推理能力，可以由部分水質指標預測蟹塘水質類型（A 類或者B 類），也可以基于已知的水質類型與部分水質指標推測某些水質指標的狀態。對測試數據集D1中任意的100 條數據實例進行模型精度測試，引入混淆矩陣，并計算其Kappa 系數［16］。Kappa 系數能衡量分類的精度，本次精度測試實驗的混淆矩陣［17］見表3。

表3 蟹塘水質分類預測與實際情況

根據表3 中的混淆矩陣，計算得本次精度測試的Kappa 系數為0.807，Kappa 系數0.8～1 屬于完全一致性標準范疇，這說明本文使用貝葉斯網絡對蟹塘水質分類狀況及水質指標的預測分析是可行的。

3 結語

本文對蟹塘水質與水質指標之間復雜的因果關系進行了貝葉斯網絡建模，遴選了9 項水質指標以及水質分類共計10 個結點構成了貝葉斯網絡結構模型，以期為水質預測或者水質指標分析提供科學依據。貝葉斯網絡結構所對應的CPT 表基于訓練數據集D 學習構建。訓練數據集D 中數據都經過自適應加權數據融合處理，精度高、誤差小。使用K2算法學習構建貝葉斯網絡。由貝葉斯網絡可知，蟹塘水質受Tw、TN、TP、NO3-_N、NH4+_N、MDA六項水質指標直接影響，因果關系級別較高，對該六項水質指標應作重點監測管理。模型精度測試Kappa系數0.807，表明本文使用貝葉斯網絡對蟹塘水質分析預測是準確可行的。