具有參數不確定離散系統的魯棒性能分析

劉旭遙

（吉林師范大學 數學學院，吉林 長春 136000）

0 引 言

離散系統在綜合與分析問題上的研究，目前國內外學者已經取得了較好的研究成果[1-8]。但是，與具有參數不確定離散系統的魯棒性能相關聯的結果仍然存在很多不足，需要進一步補充和完善。文獻[9-11]應用離散時間系統的分析和設計方法分析和設計控制系統，但是由于非線性系統本身具有一定的復雜性，往往對其進行穩定性分析和控制造成困難。本文采用Lyapunov函數方法，結合線性矩陣不等式技術，得出不確定離散系統等價的線性矩陣不等式的一個充分條件。

1 問題描述

針對具有參數不確定性的離散系統：

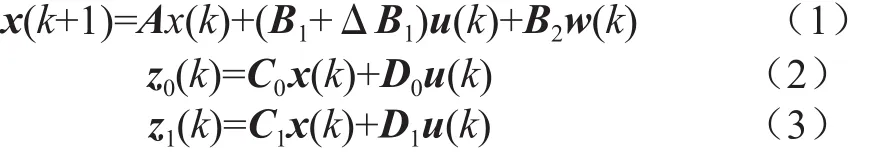
其中，x(k)∈Rn是狀態向量，u(k)∈Rm是控制輸入，w(k)∈Rp是外部干擾輸入，z0(k)∈Rq、z1(k)∈Rr是調整后的輸出，A、B1、B2、C0、C1、D0和D1是實常數矩陣，ΔB1是不確定實矩陣，具有以下形式：

γ＞0為狀態反饋控制律，有：

得到閉環系統：

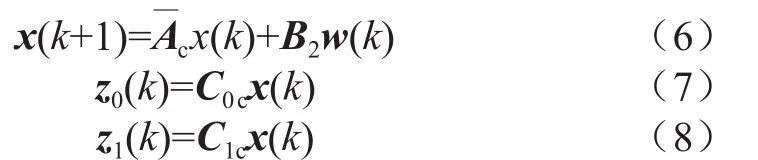
引理1：給定適當維數的矩陣Y、D和E，其中Y是對稱的，則Y+DFE+ETFTDT＜0。對于所有滿足FTF≤I的矩陣F，當且僅當存在常數ε＞0時，則Y+εDDT+ ＜ε-1ETE0。

定理1：給定一個常數γ＞0和式（8），A—c漸近穩定，且||T(z)||∞＜γ，當且僅當存在常數α＞0，則：

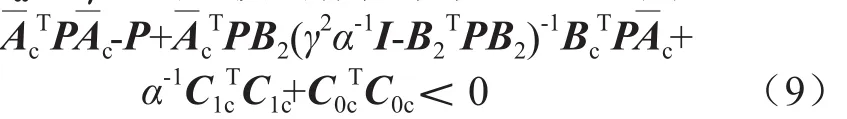
有一個正定矩陣P，所以γ2α-1I-B2TPB2＞0，則：

2 主要成果

定理2：存在常數α＞0和對稱正定矩陣P，使得式（9）和γ2α-1I-B2TPB2＞0成立。當且僅當存在常數α、β＞0和對稱正定矩陣X時，有：

證明：根據矩陣的schur補充性質，矩陣不等式（9）和γ2α-1I-B2TPB2＞0成立，則：

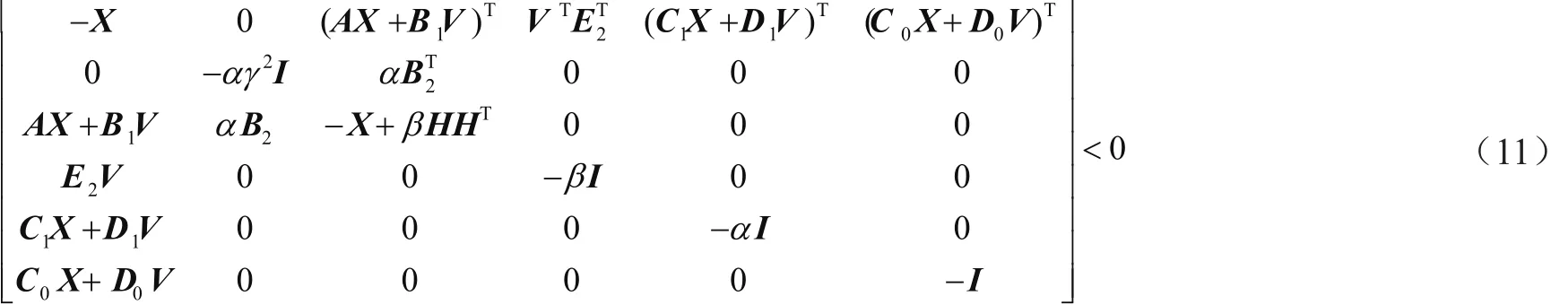
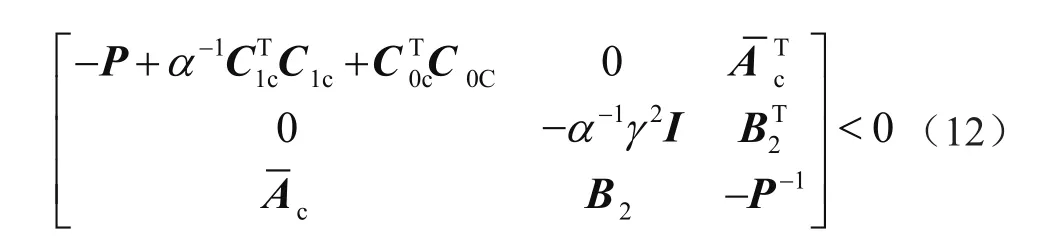
記：

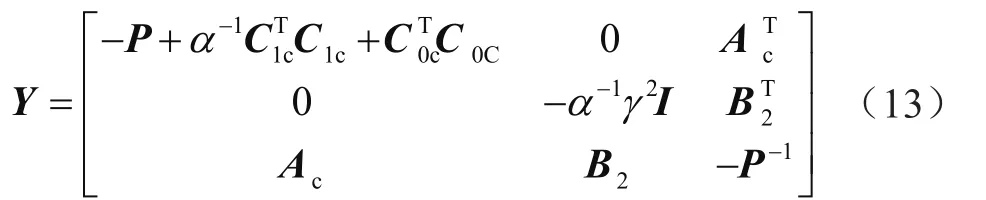
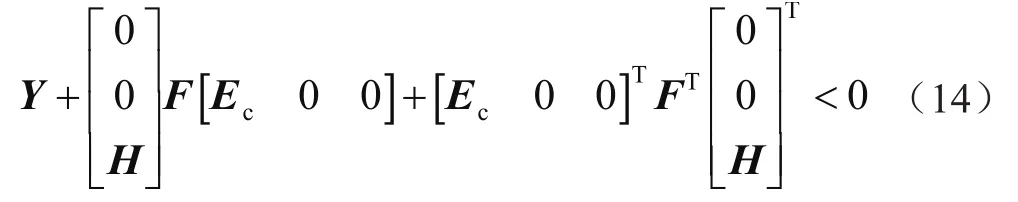
通過引理1，當且僅當存在常數β＞0時，有：

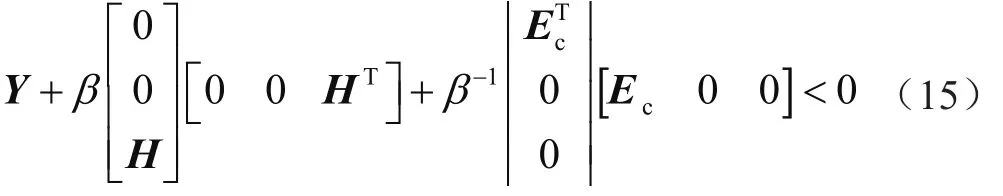
進一步應用schur補充屬性，并代入矩陣Y的表達式，有：

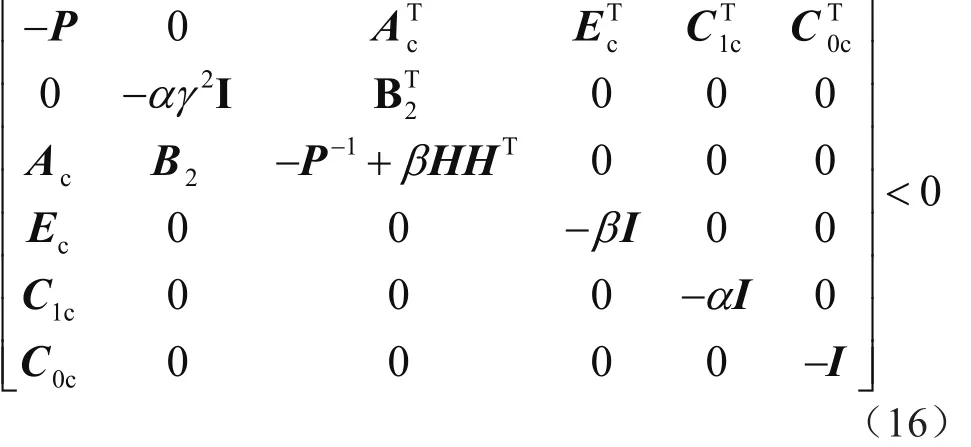
將上述六階矩陣左乘和右乘矩陣diag{P-1,αI,I,I,I,I}，并記X=P-1，C0c=C0+D0VX-1，C1c=C1+D1VX-1，Ac=A+B1VX-1來獲得式（11）。

3 結 論

針對具有參數不確定離散系統，利用Lyapunov函數方法，結合線性矩陣不等式技術，在引理1的基礎上，得出了不確定離散系統等價的線性矩陣不等式的一個充分條件。