基于自適應(yīng)跟蹤控制的系統(tǒng)頻率調(diào)整策略

何曉峰，姚文峰，黎壽濤，夏成軍，程韌俐，黃東啟，馬偉哲

（1.深圳供電局有限公司，廣東 深圳 518001；2.南方電網(wǎng)科學(xué)研究院有限責(zé)任公司，廣東 廣州 510663；

3.華南理工大學(xué) 電力學(xué)院，廣東 廣州 510640）

0 引 言

高壓直流輸電聯(lián)于弱交流系統(tǒng)時，系統(tǒng)頻率控制是一項(xiàng)極大的技術(shù)挑戰(zhàn)。典型運(yùn)行工況包括：直流孤島運(yùn)行方式；受端交流系統(tǒng)故障可能引發(fā)逆變器換相失敗，且在故障清除時往往導(dǎo)致受端系統(tǒng)進(jìn)一步變?nèi)鮗1]；電網(wǎng)黑啟動過程中，利用直流輸電系統(tǒng)加快電網(wǎng)恢復(fù)[2]。

高壓直流輸電配置有頻率限制器（Frequency Limit Control，F(xiàn)LC）。孤島運(yùn)行方式下，采用FLC增強(qiáng)孤島系統(tǒng)頻率的穩(wěn)定性[3-6]。頻率調(diào)整策略通常采用直流功率跟隨機(jī)組功率方式，并要合理設(shè)置FLC動作死區(qū)和發(fā)電機(jī)調(diào)速器參數(shù)，以解決由于動作不協(xié)調(diào)引發(fā)的頻率周期性振蕩問題[7-9]。利用FLC還可以抑制風(fēng)電功率波動，提高故障后的系統(tǒng)穩(wěn)定性[10-11]。

在黑啟動期間，HVDC的送受端均聯(lián)于弱交流系統(tǒng)。HVDC應(yīng)用于黑啟動，需要滿足一定的技術(shù)條件[2]。文獻(xiàn)[12]對黑啟動過程中HVDC啟動條件及頻率控制策略進(jìn)行了研究，但未考慮送端系統(tǒng)，僅適用于受端系統(tǒng)黑啟動情況。文獻(xiàn)[13]研究并提出黑啟動過程中高壓直流輸電的變參數(shù)FLC控制策略，但在黑啟動過程中，最優(yōu)FLC參數(shù)將隨等值機(jī)組參數(shù)和系統(tǒng)容量變化，意味著要頻繁優(yōu)化FLC參數(shù)。

本文提出基于自適應(yīng)跟蹤控制的系統(tǒng)頻率協(xié)調(diào)控制策略。針對電網(wǎng)黑啟動過程中交流系統(tǒng)容量和等值機(jī)組參數(shù)不斷變化的場景，基于自適應(yīng)跟蹤控制，使實(shí)際系統(tǒng)頻率跟隨參考系統(tǒng)的頻率輸出動態(tài)變化，從而實(shí)現(xiàn)參數(shù)未知系統(tǒng)的頻率協(xié)調(diào)控制。

1 數(shù)學(xué)模型

黑啟動過程中，HVDC成功啟動后，系統(tǒng)如圖1所示，兩側(cè)交流系統(tǒng)分別等值為發(fā)電機(jī)串聯(lián)阻抗，通過HVDC異步互聯(lián)。

圖1 等值系統(tǒng)示意圖

水輪機(jī)、燃?xì)廨啓C(jī)、小火電機(jī)組是常見的黑啟動電源。本文采用水輪發(fā)電機(jī)作為黑啟動電源，其他機(jī)組可類似分析，只是發(fā)電機(jī)組參數(shù)取值不同。水輪發(fā)電機(jī)組的傳遞函數(shù)[13-14]如圖2所示，各參數(shù)的取值范圍[13，15-16]如表1所示。

圖2中的狀態(tài)變量xn（n為1～5）的含義：x2是導(dǎo)葉開度，x3是原動機(jī)輸出的機(jī)械功率，x4是頻率，

圖2 水輪發(fā)電機(jī)組的傳遞函數(shù)

表1 參數(shù)的取值范圍

式中，下標(biāo)s可為r或i，分別表示整流側(cè)或逆變側(cè)。在擾動初始時刻t0，有：

圖1中，整流側(cè)、逆變側(cè)發(fā)電機(jī)的輸出功率為：

式中，ΔPLr和ΔPLi分別為兩側(cè)負(fù)荷的變化量，Sr和Si分別是整流側(cè)、逆變側(cè)發(fā)電機(jī)的額定容量；ΔPd為直流功率變化量。

換流器可表示成一階慣性環(huán)節(jié)[17]，如式（4）所示。其中，T為換流器的慣性時間常數(shù)，ΔPord為直流功率指令變化量，ΔPd為直流功率變化量。

式（1）～式（4）構(gòu)成了本文分析用的數(shù)學(xué)模型。

2 直流最優(yōu)傳輸功率

若圖1中系統(tǒng)參數(shù)已知，可以采用線性二次型最優(yōu)控制方法[18]求解得到最優(yōu)的直流傳輸功率指令變化量ΔPord，使得送受端負(fù)荷ΔPLr或ΔPLi投入后兩側(cè)交流系統(tǒng)的頻率偏移最小。

令：

在黑啟動過程中，負(fù)荷是緩慢投入的，因此可近似認(rèn)為ΔPLs的導(dǎo)數(shù)為0。于是，得到新微分方程組、新狀態(tài)變量初值為：

輸出量為：

將式（6）寫成矩陣形式，即：

新狀態(tài)方程的理想輸出為：

在交流負(fù)荷投入后，同步控制HVDC的傳輸功率，使得兩側(cè)交流系統(tǒng)的頻率偏移均盡可能小。優(yōu)化目標(biāo)為：

式中M為正定矩陣：

e為跟蹤誤差：

對ΔPord的取值沒有限制，N可盡可能小[19]，本文取0.001。

根據(jù)線性最優(yōu)控制理論，可以設(shè)計(jì)出直流輸送功率的最優(yōu)控制規(guī)律：

K和g可以通過求解黎卡提方程得到：

為驗(yàn)證式（14）直流輸送功率最優(yōu)控制規(guī)律，采用文獻(xiàn)[13]中的仿真模型和參數(shù)，將本文所提最優(yōu)控制方法與文獻(xiàn)[13]中的最優(yōu)參數(shù)FLC控制下的結(jié)果進(jìn)行對比，結(jié)果如圖3所示。

圖3 兩種頻率調(diào)整方法下負(fù)荷投入后波形

仿真結(jié)果表明，兩種方法得到的直流傳輸功率指令曲線基本相同，頻率曲線也基本相同。但是，本文提出的最優(yōu)控制方法只需求解黎卡提方程便可得到直流最優(yōu)傳輸功率，無需在FLC參數(shù)優(yōu)化中多次求解狀態(tài)方程，較文獻(xiàn)[13]方法計(jì)算更加簡單。

可以估算頻率約束的最大可投負(fù)荷ΔPLsmax：

式中Δflim是頻率偏移極限值，Δf0max是當(dāng)負(fù)荷擾動ΔPLs為0.01 p.u.時直流最優(yōu)傳輸功率下的系統(tǒng)最大頻率偏移量。

3 黑啟動過程中系統(tǒng)頻率的協(xié)調(diào)控制

上述分析是針對系統(tǒng)參數(shù)已知的情況。黑啟動過程中系統(tǒng)參數(shù)持續(xù)變化，無法準(zhǔn)確辨識。此時，將無法直接通過線性二次型最優(yōu)控制方法求解最優(yōu)的直流傳輸功率，因而無法確定交流系統(tǒng)可投入的最大負(fù)荷。同時，由于參數(shù)未知，無法求解最優(yōu)FLC參數(shù)，基于FLC的頻率調(diào)整方法[13]也將失效。針對這些問題，提出了一種基于自適應(yīng)跟蹤控制的系統(tǒng)頻率協(xié)調(diào)控制策略。

3.1 發(fā)電機(jī)參考模型參數(shù)的選取

在合理的參數(shù)范圍內(nèi)，選取使相同負(fù)荷投入后，頻率最大、偏移最小的發(fā)電機(jī)及其調(diào)速器的參數(shù)。

Tj和k可以根據(jù)已投入的機(jī)組計(jì)算得到，即：

受擾后，交流系統(tǒng)最大頻率偏移量隨R、Tg、Tp和Tw的增大而增大[13]，因此最優(yōu)發(fā)電機(jī)參數(shù)為取值范圍內(nèi)最小值。采用最優(yōu)發(fā)電機(jī)參數(shù)下的發(fā)電機(jī)模型作為自適應(yīng)控制器的參考系統(tǒng)。

3.2 系統(tǒng)頻率的自適應(yīng)跟蹤控制

3.2.1 Narendra自適應(yīng)跟蹤控制

采用Narendra自適應(yīng)跟蹤控制方法，使實(shí)際系統(tǒng)頻率偏移Δx4p跟蹤參考系統(tǒng)的頻率偏移Δx4m。Δx4m是參考系統(tǒng)在直流最優(yōu)傳輸功率下的頻率響應(yīng)。該方法利用被控對象實(shí)際輸出與參考系統(tǒng)理想輸出的偏差調(diào)節(jié)輸入，使實(shí)際輸出接近理想輸出[20]。只要參考系統(tǒng)的頻率響應(yīng)是最優(yōu)的，那么實(shí)際系統(tǒng)的頻率響應(yīng)也將是最優(yōu)的，無需辨識系統(tǒng)參數(shù)。

根據(jù)圖1，Δf可表示為：

其中G1(s)為頻率變化量Δf關(guān)于ΔPe的傳遞函數(shù)，G2(s)為Δf關(guān)于RΔPref的傳遞函數(shù)。

式（18）表明，可以對ΔPe和ΔPref設(shè)置控制律實(shí)現(xiàn)實(shí)際系統(tǒng)頻率偏移的跟蹤調(diào)節(jié)。本文采用Narendra自適應(yīng)控制方法，對圖1中兩側(cè)等值發(fā)電機(jī)的ΔPref設(shè)置控制律，實(shí)現(xiàn)頻率的跟蹤控制，控制框圖如圖4所示。參考系統(tǒng)輸出的導(dǎo)葉開度Δx2m與實(shí)際系統(tǒng)輸出的導(dǎo)葉開度Δx2p的偏差量e、ΔPe以及Δx2p作為Narendra自適應(yīng)控制器輸入，輸出信號RΔP0調(diào)節(jié)實(shí)際系統(tǒng)的功率參考值。

圖4 交流系統(tǒng)頻率的自適應(yīng)跟蹤控制

參考系統(tǒng)頻率與實(shí)際系統(tǒng)頻率的差值為：

要使Δx4m-Δx4p=0，則應(yīng)滿足：

其中：

令u=Δx2m-Δx2p，如圖4中虛線框所示，則滿足式（20）就可以使Δx4m-Δx4p=0，實(shí)現(xiàn)系統(tǒng)頻率的跟蹤控制。

3.2.2 非最小相位系統(tǒng)跟蹤控制器

式（21）表明，Gw是非最小相位系統(tǒng)，其逆系統(tǒng)1/Gw不穩(wěn)定。可采用文獻(xiàn)[21]中基于系統(tǒng)中心方法的非最小相位系統(tǒng)跟蹤控制方法，求u的有界解，如圖4中虛線框所示。

4 仿真驗(yàn)證

用PSCAD/EMTDC軟件搭建如圖1所示的系統(tǒng)仿真模型，系統(tǒng)參數(shù)來自文獻(xiàn)[20]。以HVDC的額定功率作為功率基準(zhǔn)，送受端等值發(fā)電機(jī)的容量分別為2 p.u.和 1 p.u.。

最優(yōu)發(fā)電機(jī)參數(shù)，如表2所示。

表2 最優(yōu)發(fā)電機(jī)參數(shù)

將該發(fā)電機(jī)模型作為等值發(fā)電機(jī)的參考模型。

4.1 確定最大可投負(fù)荷

仿真表明，當(dāng)受端負(fù)荷ΔPLi為0.01 p.u.時，最優(yōu)直流功率下的頻率偏移量Δf0max為0.046 5 Hz。根據(jù)式（16）估算，受端的最大可投負(fù)荷ΔPLsmax為0.107 5 p.u.（取頻率偏移極限Δflim為0.5 Hz）。

仿真驗(yàn)證，在受端投入負(fù)荷0.107 5 p.u.時，依據(jù)式（14）計(jì)算得到直流傳輸功率控制律，仿真得到送受端頻率f和直流功率指令增量ΔPord如圖5所示。結(jié)果表明，兩側(cè)頻率偏移量基本相同，均在頻率極限0.5 Hz以內(nèi)。

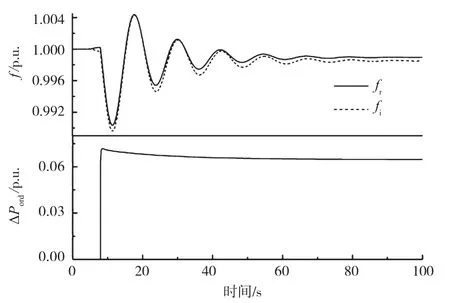
圖5 最優(yōu)參數(shù)發(fā)電機(jī)在線性二次型控制方法下的仿真結(jié)果

4.2 系統(tǒng)參數(shù)未知情況

改變發(fā)電機(jī)組參數(shù)以模擬黑啟動過程，此時系統(tǒng)參數(shù)未知。若仍然在受端投入負(fù)荷0.107 5 p.u.，控制策略不變，則送受端頻率f和直流功率指令增量ΔPord如圖6所示。

圖6 發(fā)電機(jī)參數(shù)改變后的仿真結(jié)果

圖6表明，送受端頻率偏差最大達(dá)到1.1 Hz，超過允許極限值0.5 Hz，表明在該場景下，由線性最優(yōu)控制得到的控制策略不能滿足系統(tǒng)運(yùn)行要求，根本原因在于最優(yōu)控制策略不能跟蹤系統(tǒng)參數(shù)的變化。

4.3 系統(tǒng)頻率的自適應(yīng)跟蹤控制

在上述場景下，加入如圖4所示的自適應(yīng)跟蹤控制環(huán)節(jié)，仿真結(jié)果如圖7所示。仿真結(jié)果表明，送受端頻率偏差最大值又回到0.5 Hz以內(nèi)，滿足了系統(tǒng)運(yùn)行要求。這說明自適應(yīng)跟蹤控制可以有效跟蹤參考模型輸出，適應(yīng)系統(tǒng)參數(shù)未知或不確定的場景。

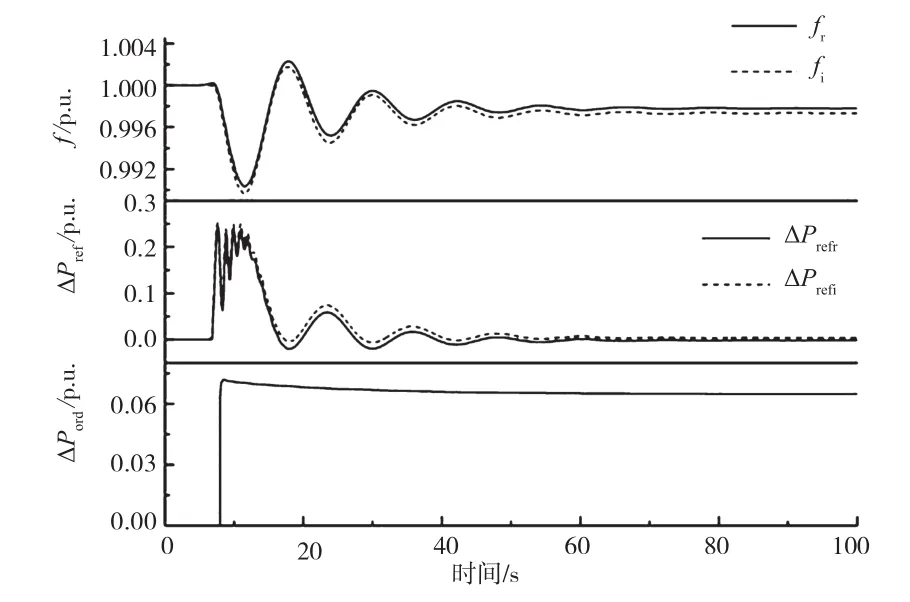
圖7 采用系統(tǒng)頻率的自適應(yīng)跟蹤控制方法的仿真結(jié)果

5 結(jié) 論

本文提出了一種綜合線性最優(yōu)控制和自適應(yīng)跟蹤控制的系統(tǒng)頻率協(xié)調(diào)控制策略，跟蹤參考模型的頻率輸出，通過協(xié)調(diào)控制兩側(cè)交流系統(tǒng)等值發(fā)電機(jī)功率參考值和直流傳輸功率，實(shí)現(xiàn)黑啟動過程中系統(tǒng)頻率的自動調(diào)整。主要結(jié)論如下：

（1）采用線性二次型最優(yōu)控制方法優(yōu)化控制直流傳輸功率，可以得到參數(shù)確定場景下的最優(yōu)控制策略，可將該參數(shù)模型和輸出特性作為系統(tǒng)參考模型和參考信號。

（2）采用自適應(yīng)跟蹤控制，使實(shí)際系統(tǒng)頻率輸出跟隨參考模型的頻率響應(yīng)，可以自適應(yīng)系統(tǒng)參數(shù)未知或參數(shù)不確定的場景。