二維耦合熱彈性動力學問題的無網格自然鄰接點Petrov-Galerkin法

李慶華 陳莘莘

摘 要：為了更有效地求解二維耦合熱彈性動力學問題，對無網格自然鄰接點Petrov-Galerkin法在此類問題中的應用進行了研究，并發展了相應的計算方法。該方法建立試函數時可以只依賴于一組離散的節點，有效地避免了復雜的網格劃分和網格畸變的影響。相對于常用的移動最小二乘而言，自然鄰接點插值不涉及復雜的矩陣求逆運算，更不需要任何人為參數。由于運動方程和瞬態熱傳導方程相互影響，這些方程必須聯立求解。采用Newmark法求解空間離散后得到的二階常微分方程組，進而可直接獲得溫度場和位移場的數值結果。

關鍵詞： 無網格法;自然鄰接點插值;耦合熱彈性動力學;Petrov-Galerkin法

中圖分類號：TP301.6 ? 文獻標志碼：A ? 文章編號：2096-6717（2019）05-0109-06

Abstract：In order to solve the two-dimensional dynamic coupled thermoelasticity problem more effectively， a novel numerical method based on the meshless natural neighbour Petrov-Galerkin method is proposed in this study. Only a group of scattered nodes are required in this method， to construct approximation function and therefore complex meshing and disadvantage of mesh distortion are effectively eliminated. In comparison with the moving least-squares （MLS） approximation used widely in meshless methods， the natural neighbour interpolation requires no complex matrix inversions and no artificial intermediate parameters. The equations of motion and transient heat conduction equations of the coupled thermoelasticity interaction on each other and therefore these equations must be solved simultaneously. After spatially discretization， a series of second-order ordinary differential algebraic equations is obtained， which is solved by the Newmark method to obtain the numerical temperature and displacement field directly.

Keywords：meshless method; natural neighbour interpolation; dynamic coupled thermoelasticity; Petrov-Galerkin method

當結構受到溫變，一般會產生熱應力，并且熱應力是物體破壞的一個重要因素[1-2]。對受熱結構進行分析時，解耦方法可先由熱傳導方程求出溫度分布，再由熱彈性方程求解位移和應力。但是，解耦方法沒有考慮結構變形對溫度場的影響[3]。事實上，熱彈性力學中最基本的問題就是耦合熱彈性問題。在耦合熱彈性問題中，溫度和變形會相互影響，溫度場和應變場的耦合項必須體現在熱傳導方程中。為了求解溫度、位移和應力，必須聯立求解熱傳導方程和熱彈性運動方程。相對于非耦合熱彈性問題，耦合熱彈性問題求解更困難。

熱應力問題的數值方法主要基于發展較為成熟的有限元法[4-5]和邊界元法[6-8]。近年來，部分學者嘗試采用無網格法[9-12]求解熱應力問題。無網格法不僅能夠避免網格生成的復雜過程，而且在節點分布不規則時，損失的計算精度較小，從而日益得到重視[13-14]。近十多年來發展起來的無網格法―無網格自然鄰接點Petrov-Galerkin法[15-16]不僅允許加權函數和試函數取自不同的函數空間[17]，而且克服了本質邊界條件不易施加的困難。此方法中，所有的積分都在中心為所考慮點的多邊形子域上進行，而且多邊形子域的構造十分方便。目前，無網格自然鄰接點Petrov-Galerkin法在很多領域都得到廣泛應用[18-20]。本文采用自然鄰接點插值對溫度和位移分別插值，與局部加權余量法結合，提出了適用于耦合熱彈性動力學問題的無網格自然鄰接點Petrov-Galerkin法。最后，通過數值算例驗證了本文方法應用于耦合熱彈性動力學問題分析的有效性和合理性。

1 自然鄰接點插值

3 數值算例

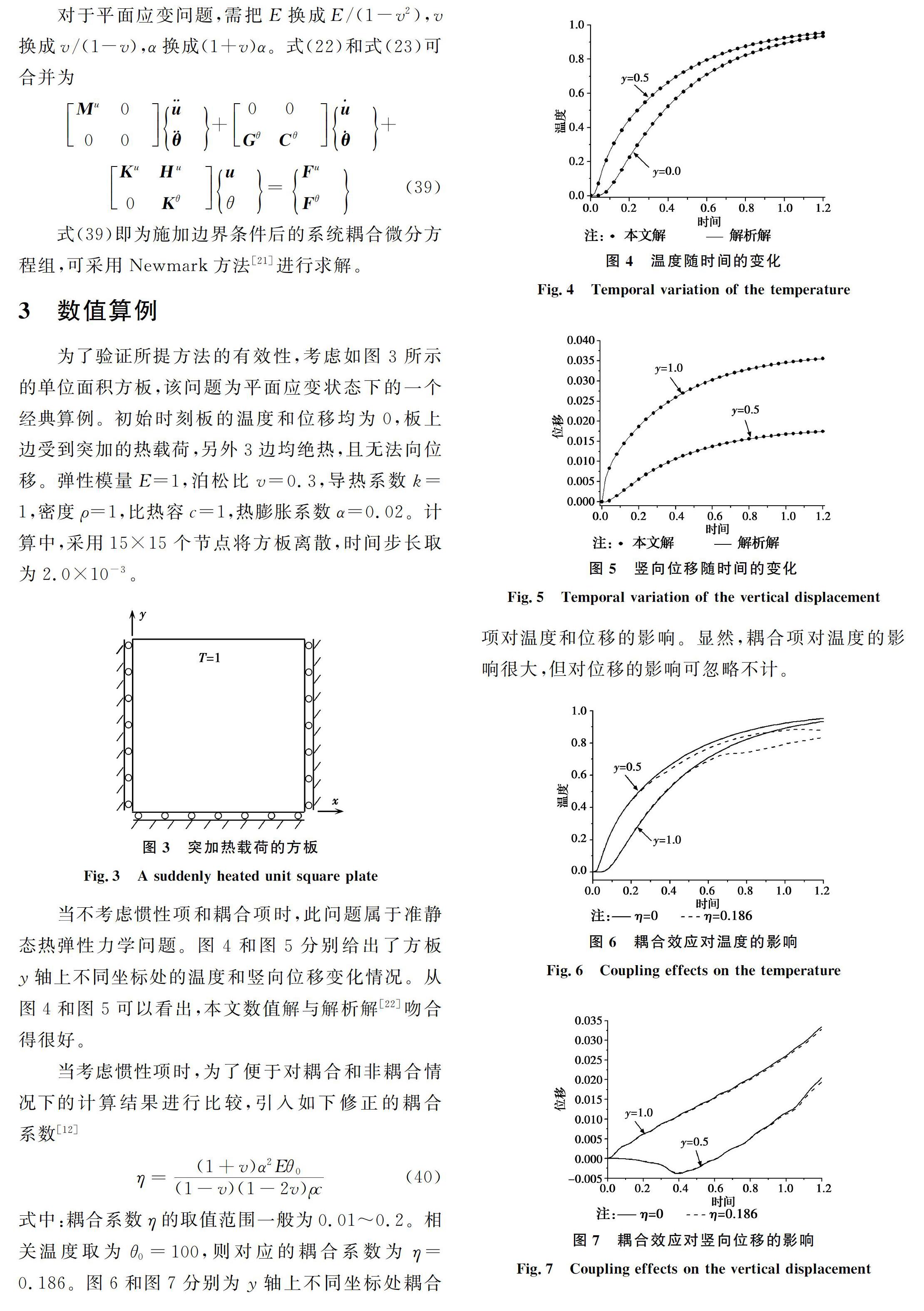
為了驗證所提方法的有效性，考慮如圖3所示的單位面積方板，該問題為平面應變狀態下的一個經典算例。初始時刻板的溫度和位移均為0，板上邊受到突加的熱載荷，另外3邊均絕熱，且無法向位移。彈性模量E=1，泊松比v=0.3，導熱系數k=1，密度ρ=1，比熱容c=1，熱膨脹系數α=0.02。計算中，采用15×15個節點將方板離散，時間步長取為2.0×10-3。

當不考慮慣性項和耦合項時，此問題屬于準靜態熱彈性力學問題。圖4和圖5分別給出了方板y軸上不同坐標處的溫度和豎向位移變化情況。從圖4和圖5可以看出，本文數值解與解析解[22]吻合得很好。

[12] ZHENG B J， GAO X W， YANG K， et al. A novel meshless local Petrov-Galerkin method for dynamic coupled thermoelasticity analysis under thermal and mechanical shock loading [J]. Engineering Analysis with Boundary Elements， 2015， 60： 154-161.

[13] 高欣， 段慶林， 李書卉， 等. 裂紋問題的一致性高階無網格法[J]. 計算力學學報， 2018， 35（3）： 275-282.

GAO X， DUAN Q L， LI S H， et al. Consistent high order meshfree method for crack problems [J]. Chinese Journal of Computational Mechanics， 2018， 35（3）： 275-282.（in Chinese）

[14] 王東東， 張漢杰， 梁慶文. 等幾何修正準凸無網格法[J]. 計算力學學報， 2016， 33（4）： 605-612.

WANG D D， ZHANG H J， LIANG Q W. Isogeometric refined quasi-convex meshfree method [J]. Chinese Journal of Computational Mechanics， 2016， 33（4）： 605-612. （in Chinese）

[15] CAI Y C， ZHU H H. A meshless local natural neighbour interpolation method for stress analysis of solids [J]. Engineering Analysis with Boundary Elements， 2004， 28（6）： 607-613.

[16] WANG K， ZHOU S J， SHAN G J. The natural neighbour Petrov-Galerkin method for elasto-statics [J]. International Journal for Numerical Methods in Engineering， 2005， 63（8）： 1126-1145.

[17] ATLURI S N， ZHU T. A new meshless local petrov-galerkin （MLPG） approach in computational mechanics [J]. Computational Mechanics， 1998， 22（2）： 117-127.

[18] 李順利， 龍述堯， 李光耀， 等. 自然鄰接點局部Petrov-Galerkin法求解中厚板彎曲問題[J]. 湖南大學學報（自然科學版）， 2011， 38（1）： 53-57.

LI S L， LONG S Y， LI G Y， et al. Natural neighbor petrov-galerkin method for moderately thick plates [J]. Journal of Hunan University（Natural Sciences）， 2011， 38（1）： 53-57.（in Chinese）

[19] 王凱， 周慎杰， 聶志峰， 等. 基于局部自然鄰近無網格法的形狀優化[J]. 機械工程學報， 2009， 45（10）： 185-191.

WANG K， ZHOU S J， NIE Z F， et al. Shape optimization based on the local natural neighbor Petrov-Galerkin method [J]. Journal of Mechanical Engineering， 2009， 45（10）： 185-191.（in Chinese）

[20] 陳莘莘， 李慶華， 劉永勝. 軸對稱動力學問題的無網格自然鄰接點Petrov-Galerkin法 [J]. 振動與沖擊， 2015， 34（3）： 61-65.

CHEN S S， LI Q H， LIU Y S. Meshless natural neighbour Petrov-Galerkin method for axisymmetric dynamic problems [J]. Journal of Vibration and Shock， 2015， 34（3）： 61-65. （in Chinese）

[21] 張亞輝， 林家浩. 結構動力學基礎[M]. 遼寧 大連： 大連理工大學出版社，2007.

ZHANG Y H， LIN J H. Fundamentals of structural dynamics [M]. Dalian， Liaoning： Dalian University of Technology Press， 1993. （in Chinese）

[22] CARSLAW H S， JAEGER J C. Conduction of Heat in Solids [M]. Clarendon： Oxford University Press， 1959.

（編輯 王秀玲）